深さ優先探索

And, for the hous is crinkled to and fro,

And hath so queinte weyes for to go――

For hit is shapen as the mase is wroght――

Therto have I a remedie in my thoght,

That, by a clewe of twyne, as he hath goon,

The same wey he may returne anoon,

Folwing alwey the threed, as he hath come.

――Geoffrey Chaucer, The Legend of Good Women (c. 1385)

"Com'è bello il mondo e come sono brutti i labirinti!" dissi sollevato.

"Come sarebbe bello il mondo se ci fosse una regola per girare nei labirinti," rispose il mio maestro.

[「世界の美しさよ、迷宮の醜さよ！」安心して私は言った。

「迷宮を通り抜ける手続きがある世界の美しさよ」師は答えた。]

――Umberto Eco, Il nome della rosa (1980), William Weaver による英訳 (The Name of the Rose, 1983)

前章では有向・無向両方のグラフに使える一般的な走査アルゴリズム ――何か優先探索―― を考えました。この章では、深さ優先探索 (depth first search, DFS) というこのアルゴリズムのインスタンスの一つと、この探索アルゴリズムの有向グラフに対する振る舞いに焦点を当てます。

深さ優先探索は「スタックを使った何か優先探索」と言うのが最も正確ですが、実装されるときにはスタックではなく再帰呼び出しを使うのが普通です。次のようにします:

procedure $\texttt{DFS}$($v$)

if $v$ に印が付いていない then

$v$ に印をつける

for $v \rightarrow w$ の形をした辺 do

$\texttt{DFS}$($w$)

頂点に印がついているかを再帰的な呼び出しの前に調べることで、このアルゴリズム (の実装) を高速化できます。こう変更すると $\textsc{DFS}(v)$ が各頂点 $v$ に対して最大でも一回しか呼ばれないことが保証されるからです。アルゴリズムをさらに変更して、辺と頂点に関する好きな情報を集めるようにもできます。情報の収集に使う二つのブラックボックスなサブルーチンを $\textsc{PreVisit}$ および $\textsc{PostVisit}$ とします。これらの中身はここでは指定しません。

procedure $\texttt{DFS}$($v$)

$v$ に印を付ける

$\color{red}{\textsc{PreVisit}(v)}$

for $v \rightarrow w$ の形をした辺 do

if $w$ に印が付いていない then

$\mathit{parent}(w) \leftarrow v$

$\texttt{DFS}$($w$)

$\color{green}{\textsc{PostVisit}(v)}$

$G$ において頂点 $w$ が頂点 $v$ から到達可能であるのは ――もっと簡単に言えば、$v$ から $w$ に行けるとは―― $G$ に $v$ から $w$ への有向路が存在するときに限ることを思い出してください。$\pmb{\mathit{reach}(v)}$ で $v$ から到達可能な ($v$ を含む) 頂点の集合を表すことにすると、$\textsc{DFS}(v)$ は $\mathit{reach}(v)$ に含まれる頂点全てに印を付け、それ以外の頂点には印を付けません。

無向グラフにおける到達可能性は対称です: $v$ から $w$ に行けることと $w$ から $v$ に行けることは同値です。そのため、全ての頂点から印を消した無向グラフ $G$ に対して $\textsc{DFS}(v)$ を呼ぶと、$v$ を含む成分全てに印が付き、親へのポインタの集合はその成分の全域木を定義します。

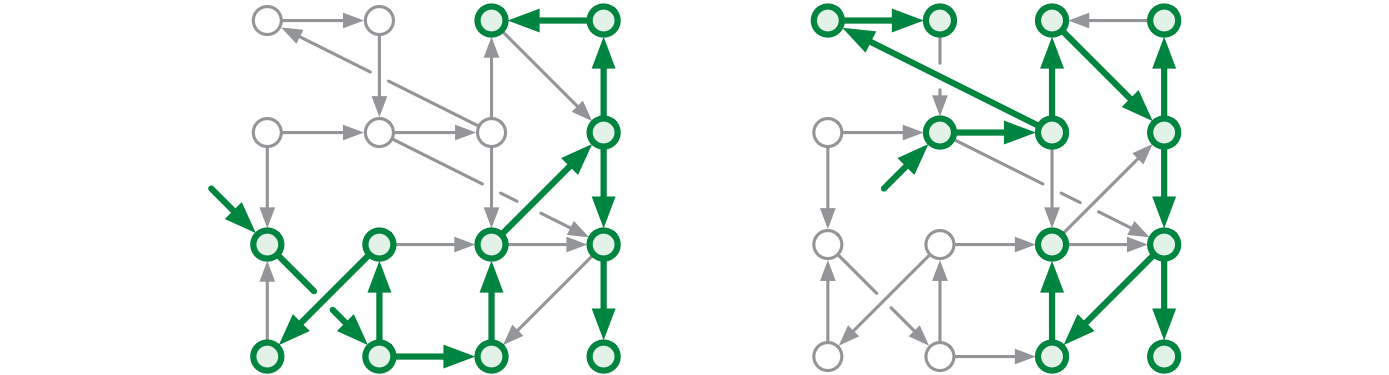
有向グラフでは状況がもう少し難しくなります。下図に示すように、グラフが "連結" であっても異なる頂点から到達可能な頂点の集合が異なり、一部だけが重なることもあります。$\textsc{DFS}(v)$ を呼んだときに定義される親子関係を示すポインタの集合は $\mathit{reach}(v)$ の全域木を定義しますが、この全域木がグラフ全体の全域木になるとは限りません。

前章でも説明しましたが、この到達可能性アルゴリズムをラッパー関数で自然に拡張することで、入力されたグラフ全体に対する走査が可能です。この走査はグラフが非連結であったとしても成功します。次に示す疑似コードでは、$\textsc{PreVisit}$ と $\textsc{PostVisit}$ のために必要な前処理をブラックボックスなサブルーチン $\textsc{Preprocess}$ で行うようにしています:

もしグラフを改変することが許されているなら、ソース (source) の頂点 $s$ と $s$ から他の全ての頂点に伸びる辺を $G$ に追加すれば $\textsc{DFS}(s)$ 一回の呼び出しで全ての頂点を走査できます。こうした場合には親に向かうポインタの集合が拡張された入力グラフの全域木を必ず定義しますが、これは元のグラフに対する全域木ではありません。

procedure $\texttt{DFSAll}$($G$)

$\color{#2D2F91}{\textsc{Preprocess}(G)}$

for 頂点 $v$ do

$v$ の印を消す

for 頂点 $v$ do

if $v$ に印が付いていない then

$\texttt{DFS}$($v$)

procedure $\texttt{DFSALL}$($G$)

$\color{#2D2F91}{\textsc{Preprocess}(G)}$

新しい頂点 $s$ を $G$ に加える

for 頂点 $v$ do

辺 $s \rightarrow v$ を $G$ に加える

$v$ の印を消す

$\texttt{DFS}$($s$)

図 6.2

深さ優先探索に対する二つの一般的なラッパーアルゴリズム

出来上がる全域木が異なる点を除けば二つのラッパー関数は同じ動作をするので、好きな方を使うことができます¹。

このアルゴリズムも無向グラフと有向グラフに対する動作に違いがあります。前章で見た通り、無向グラフでは $\textsc{DFSAll}$ を使ってグラフの成分の数を簡単に数えることができます。具体的には、$\textsc{DFSAll}$ によって計算される親へのポインタの集合が入力グラフに対する全域森を計算し、全域森に含まれる木のそれぞれがグラフの成分の全域木に対応します。しかし有向グラフでは、グラフが "連結" だったとしても $\textsc{DFSAll}$ によって計算される "成分" の数は $1$ から $V$ までのどの数でもあり得ます。正確な数はグラフの構造とラッパーアルゴリズムにおいて頂点を選ぶ順序に依存します。

行きがけ順と帰りがけ順

根付き木に対する深さ優先探索によって行きがけ順 (preorder) および帰りがけ順 (postorder) が定義できることは知っているはずです。同じような走査順序は任意の (連結であるとは限らない) 有向グラフに対しても定義できます。次のようにカウンターを使います:

procedure $\texttt{DFSAll}$($G$)

$\color{#2D2F91}{\mathit{clock} \leftarrow 0}$

for 頂点 $v$ do

$v$ の印を消す

for 頂点 $v$ do

if $v$ に印が付いていない then

$\mathit{clock} \leftarrow$$\texttt{DFS}$($v, \mathit{clock}$)

procedure $\texttt{DFS}$($v, \mathit{clock}$)

$v$ に印を付ける

$\color{red}{\mathit{clock} \leftarrow \mathit{clock} + 1;\ \mathit{v.pre} \leftarrow \mathit{clock}}$

for $v \rightarrow w$ の形をした辺 do

if $w$ に印が付いていない then

$\mathit{parent}(w) \leftarrow v$

$\texttt{DFS}$($w$)

$\color{green}{\mathit{clock} \leftarrow \mathit{clock} + 1;\ \mathit{v.post} \leftarrow \mathit{clock}}$

図 6.3

深さ優先探索を使った行きがけ順と帰りがけ順の定義

一般的な深さ優先探索に対して $\textsc{Preprocess}$, $\textsc{PreVisit}$, $\textsc{PostVisit}$ を次のように定義しても同じアルゴリズムを得ることができます:

procedure $\texttt{Preprocess}$($G$)

$\color{#2D2F91}{\mathit{clock} \leftarrow 0}$

procedure $\texttt{PreVisit}$($v$)

$\color{red}{\mathit{clock} \leftarrow \mathit{clock} + 1}$

$\color{red}{\mathit{v.pre} \leftarrow \mathit{clock}}$

procedure $\texttt{PostVisit}$($v$)

$\color{green}{\mathit{clock} \leftarrow \mathit{clock} + 1}$

$\color{green}{\mathit{v.post} \leftarrow \mathit{clock}}$

このアルゴリズムは $v$ を再帰スタックに積んだときに $\mathit{v.pre}$ を代入し (そして $\mathit{clock}$ を進め)、再帰スタックから $v$ を取り出したときに $\mathit{v.post}$ を代入し (そして $\mathit{clock}$ を進め) ます。任意の二つの頂点 $u, v$ に対して、二つの区間 $[\mathit{u.pre}, \mathit{u.post}]$ と $[\mathit{v.pre}, \mathit{v.post}]$ は重ならないか、そうでなければ片方がもう一方に含まれることが示せます。さらに、$[\mathit{u.pre}, \mathit{u.post}]$ が $[\mathit{v.pre}, \mathit{v.post}]$ を含むことは $\textsc{DFS}(v)$ が $\textsc{DFS}(u)$ の実行中に呼ばれることと同値で、さらに親をたどるポインタの集合からできる森において $u$ が $v$ の祖先であることとも同値です。

$\textsc{DFSAll}$ がグラフの全ての頂点にラベルを付け終わると、$\mathit{v.pre}$ は頂点の行きがけ順序 (preordering) を定義し、$\mathit{v.post}$ は頂点の帰りがけ順序 (postordering) を定義します²。いくつかの自明な例外を除けば、グラフは複数の行きがけ順序と複数の帰りがけ順序を持ちます。$\textsc{DFS}$ がある頂点から出る辺を考えるときの順番や $\textsc{DFSAll}$ が頂点を考えるときの順番によって順序が変化するためです。

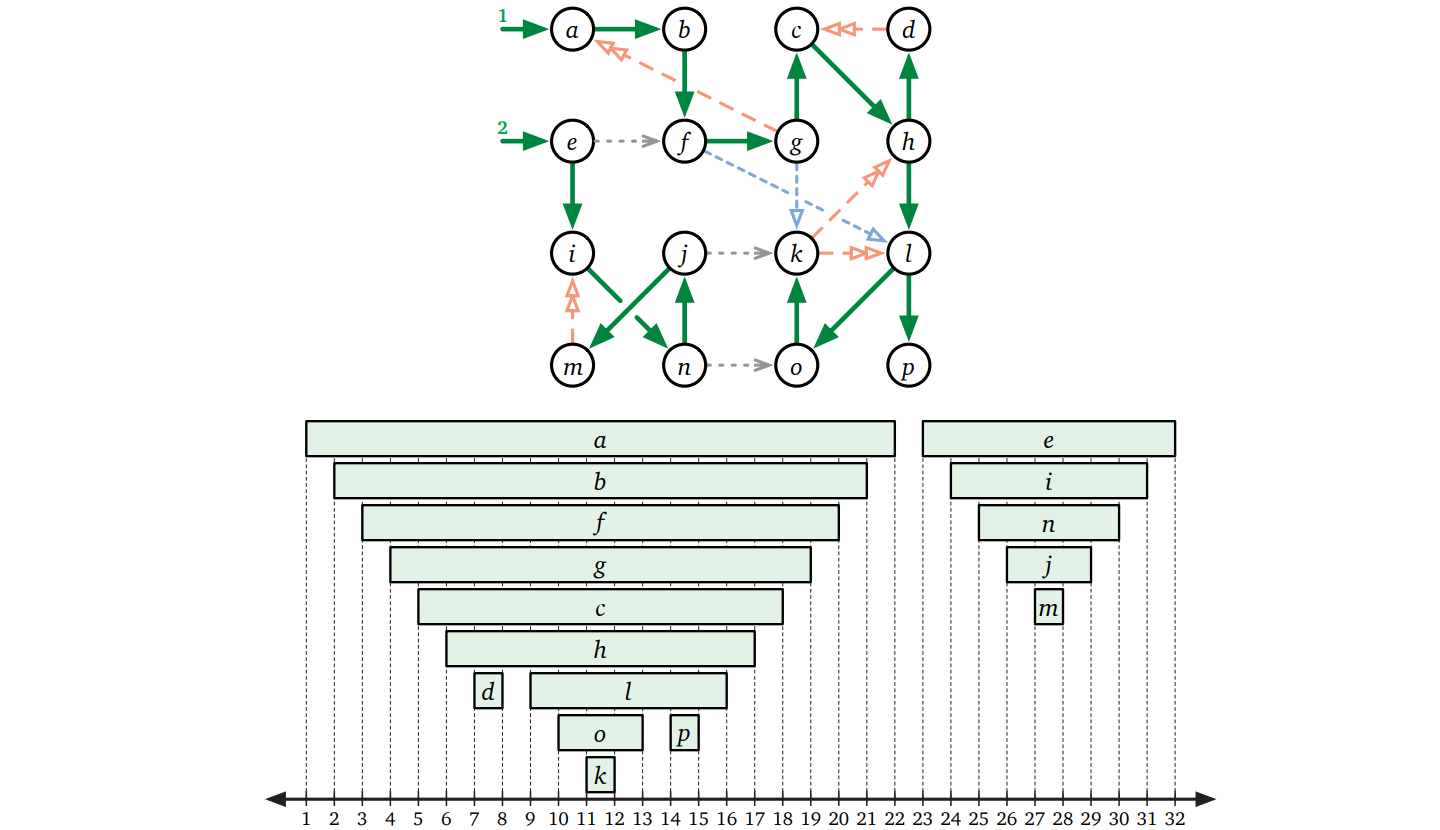
有向グラフの深さ優先探索と、それに対応する頂点のアクティブな区間。この探索によって行きがけ順序 <strong>abfgchdlokpeinjm</strong> と帰りがけ順序 <strong>dkoplhcgfbamjnie</strong> が定義される。森の辺が実践で表されている。破線の意味は次の図を参照。 — 図 6.4

有向グラフの深さ優先探索と、それに対応する頂点のアクティブな区間。この探索によって行きがけ順序 **abfgchdlokpeinjm** と帰りがけ順序 **dkoplhcgfbamjnie** が定義される。森の辺が実践で表されている。破線の意味は次の図を参照。

この章の残りの部分では、$\mathit{v.pre}$ を $\pmb{v}$ の開始時刻 (あるいは少しくだけて「$v$ が始まるとき」)、$\mathit{v.post}$ を $\pmb{\mathit{v}}$ の終了時刻 (あるいは少しくだけて「$v$ が終わるとき」)、開始時刻と終了時刻の間の区間をアクティブな区間 (あるいは少しくだけて「$v$ がアクティブな間」) と呼ぶことにします。

頂点と辺の分類

$\textsc{DFSAll}$ の実行中、入力グラフの各頂点 $v$ は次の状態のうちどれかにあります:

未処理: $\textsc{DFS}(v)$ が呼ばれていない。つまり $\mathit{clock} < \mathit{v.pre}$ が成り立つ。
アクティブ: $\textsc{DFS}(v)$ が呼ばれ、まだ返っていない。つまり $\mathit{v.pre} \leq$ $\mathit{clock} < \mathit{v.post}$ が成り立つ。
処理済: $\textsc{DFS}(v)$ が返った。つまり $\mathit{v.post} \leq \mathit{clock}$ が成り立つ。

開始時刻と終了時刻が再帰スタックのプッシュとプルに対応していることから、頂点がアクティブなのはそれが再帰スタックにあるときです。またアクティブな頂点の集合に含まれる全ての頂点を通る $G$ の有向路が常に存在することが示せます。

入力グラフの辺 $u \rightarrow v$ は、$u, v$ のアクティブな区間がどう交わるかによって次の四つに分類できます:

$\textsc{DFS}(u)$ が始まったときに $v$ が未処理な場合、$\textsc{DFS}(v)$ は $\textsc{DFS}(u)$ の実行中に直接または追加の再帰呼び出しを挟んで間接的に呼ばれる。どちらの場合においても、$u$ は $v$ の真の先祖であり、$\mathit{u.pre} < \mathit{v.pre} < \mathit{v.post} < \mathit{u.post}$ が成り立つ。
- $\textsc{DFS}(u)$ が $\textsc{DFS}(v)$ を直接呼ぶ場合、$u = \mathit{v.parent}$ であり、このような $u \rightarrow v$ を木辺 (tree edge) と呼ぶ。
- そうでなければ、$u \rightarrow v$ を前方辺 (forward edge) と呼ぶ。
$\textsc{DFS}(u)$ が始まった時に $v$ がアクティブな場合、$v$ は既に再帰スタックに載っている。したがって逆の包含関係 $\mathit{v.pre} < \mathit{u.pre} < \mathit{u.post} < \mathit{v.post}$ が成り立つ。加えて $G$ は $v$ から $u$ に向かう有向路を持つ。この条件を満たす辺 $u \rightarrow v$ を後方辺 (backward edge) と呼ぶ。
$\textsc{DFS}(u)$ が始まった時に $v$ が処理済みのとき、直ちに $\mathit{v.post} < \mathit{u.pre}$ が分かる。この条件を満たす辺 $u \rightarrow v$ を交差辺 (cross edge) と呼ぶ。
最後に、四つ目の順序 $\mathit{u.post} < \mathit{v.pre}$ はあり得ない。

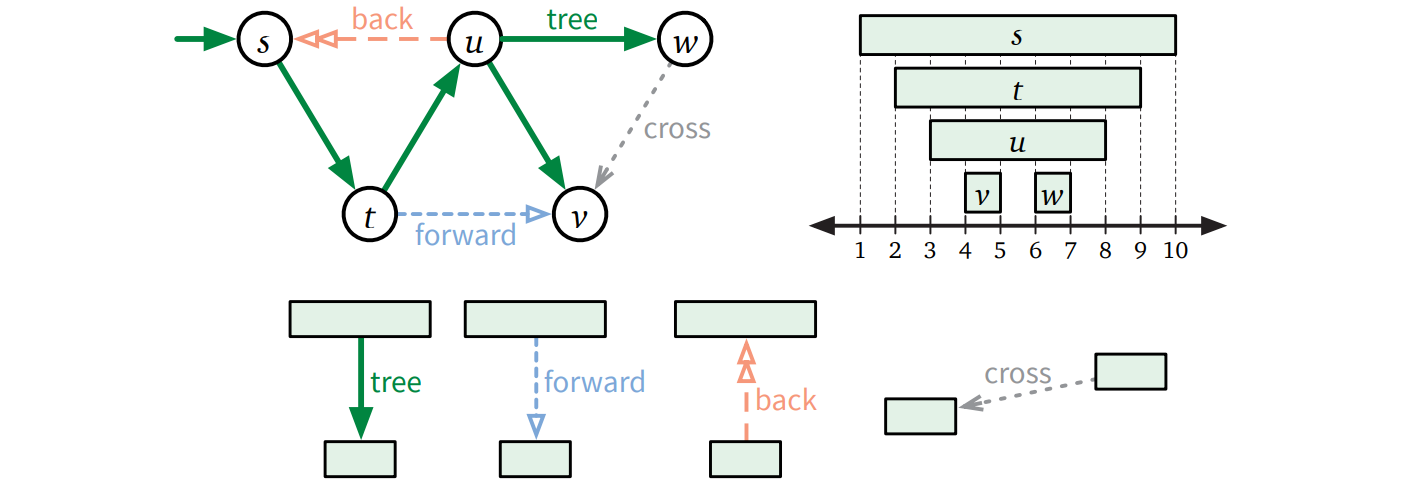
この辺の分類を下図に示します。ここでも、実際の辺の分類は $\textsc{DFSAll}$ が頂点を考える順番と $\textsc{DFS}$ が各頂点から出る辺を考える順番で変化します。

命題 6.1 有向グラフ $G$ の任意の深さ優先走査を一つ固定する。$G$ の任意の二つの頂点 $u, v$ について、次の命題は同値である。

深さ優先木において $u$ が $v$ の先祖である。
$\mathit{u.pre} \leq \mathit{v.pre} < \mathit{v.post} \leq \mathit{u.post}$
$\textsc{DFS}(v)$ が呼ばれたとき、$u$ はアクティブである。
$\textsc{DFS}(u)$ が呼ばれる直前、$u$ から $v$ への路であって $u, v$ を含む全ての頂点が未処理のものが存在する。

証明まず深さ優先木において $u$ が $v$ の先祖だと仮定する。定義により $u$ から $v$ への路 $P$ が存在する。路の長さに関する帰納法により、$\mathit{u.pre} \leq$ $\mathit{w.pre} <$ $\mathit{w.post} \leq \mathit{u.post}$ が $P$ に含まれる全ての頂点 $w$ について成り立ち、したがって $\textsc{DFS}(u)$ が呼ばれたとき $P$ の全ての頂点は未処理である。前述の不等式から $\mathit{u.pre} \leq$ $\mathit{v.pre} < $ $\mathit{v.post} \leq \mathit{u.post}$ が成り立ち、さらに $\textsc{DFS}(v)$ が実行されているとき $u$ はアクティブである。

親へ向かうポインタが再帰呼び出しを意味していることから、$\mathit{u.pre} \leq$ $\mathit{v.pre} <$ $\mathit{v.post} \leq$ $\mathit{u.post}$ は $u$ が $v$ の先祖であることを意味する。

$\textsc{DFS}(v)$ が呼ばれたとき $u$ がアクティブならば、直ちに $\mathit{u.pre} \leq$ $\mathit{v.pre} <$ $\mathit{v.post} \leq$ $\mathit{u.post}$ が分かる。

最後に、深さ優先探索木において $u$ が $v$ の先祖でないと仮定する。$u$ から $v$ への路 $P$ を固定し、$x$ を $P$ の頂点の中で $u$ の子孫でない最初の頂点、$w$ を $P$ における $x$ の前者とする。辺 $w \rightarrow x$ が存在するので $\mathit{x.pre} < \mathit{w.post}$ が成り立つ。また $w$ が $u$ の子孫であることから $\mathit{w.post} < \mathit{u.post}$ であり、よって $\mathit{x.pre} < \mathit{u.post}$ である。さらに $x$ が $u$ の子孫でないことから $\mathit{x.pre} < \mathit{u.pre}$ が分かる。アクティブな区間同士が共通部分を持つとき、片方がもう一方を真に含むことから、$u$ と $x$ の区間について二つの可能性がある:

$\mathit{u.post} < \mathit{x.post}$ の場合、$\textsc{DFS}(u)$ が呼ばれたとき $x$ はアクティブである。
$\mathit{x.post} < \mathit{u.pre}$ の場合、$\textsc{DFS}(u)$ が呼ばれたとき $x$ は終了している。

つまり $u$ から $v$ への任意の路には $\textsc{DFS}(u)$ が呼ばれた時点で未処理でない頂点が含まれる。 $\Box$

閉路の検出

閉路を含まない有向グラフを有向非巡回グラフ (directed acyclic graph, DAG)と呼びます。ある頂点に向かう辺が無い場合、その頂点をソース (source) と言い、ある頂点から出る辺が無い場合、その頂点をシンク (sink) と言います。辺が一つも付いていない孤立した頂点はソースかつシンクです。任意の DAG には少なくとも一つのソースとシンクがありますが、複数あることもあります: 例えば辺が無いグラフでは全ての頂点がソースかつシンクです。

図 6.6

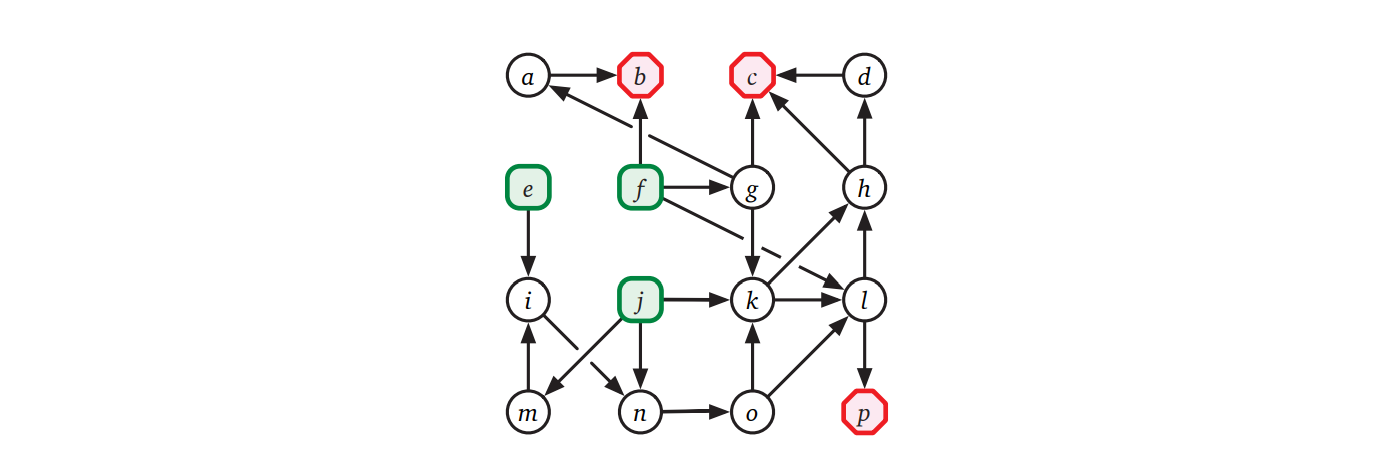
有向非巡回グラフ (頂点 $e, f, j$ がソース、頂点 $b,c,p$ がシンク)

前節で示した、$\mathit{u.post} < \mathit{v.post}$ を満たす任意の辺 $u \rightarrow v$ には $v$ から $u$ への有向路があるという事実を思い出してください。この事実を使えば、頂点を帰りがけ順に並べてから全ての辺を総当たりで調べることで与えられた有向グラフが DAG かどうかを $O(V+E)$ 時間で判定できます。

頂点に番号を振っていく代わりに頂点の状態を直接管理して、アクティブな頂点への辺が検出された時点で $\textsc{False}$ を返すようにしても同様に閉路を検出できます。このアルゴリズムの実行時間も $O(V+E)$ です。

procedure $\texttt{IsAcyclic}$($G$)

for 頂点 $v$ do

$\mathit{v.status} \leftarrow \textsc{New}$

for 頂点 $v$ do

if $\mathit{v.status} = \textsc{New}$ then

if $\texttt{IsAcyclicDFS}$($v$) $= \textsc{False}$ then

return $\textsc{False}$

return $\textsc{True}$

procedure $\texttt{IsAcyclicDFS}$($v$)

$\mathit{v.status} \leftarrow \textsc{Active}$

for $v \rightarrow w$ の形をした辺 do

if $\mathit{w.status} = \textsc{Active}$ then

return $\textsc{False}$

else if $\mathit{w.status} = \textsc{New}$ then

if $\texttt{IsAcyclicDFS}$($w$) $= \textsc{False}$ then

return $\textsc{False}$

$\mathit{v.status} \leftarrow \textsc{Finished}$

return $\textsc{True}$

図 6.7

グラフが非巡回かを判定する線形時間アルゴリズム

トポロジカルソート

有向グラフ $G$ のトポロジカル順序とは、頂点の間の全順序 $\prec$ であって全ての辺 $u \rightarrow v$ に対して $u \prec v$ が成り立つものを言います。くだけて言うと、トポロジカル順序とは全ての辺が右から左に行くように頂点を一列に並べたものです。$G$ が有向閉路を持っている場合にはトポロジカル順序が存在しないのは定義から明らかです ――閉路に含まれる頂点のうち一番右にある頂点からは左に向かう辺が出てしまいます！

有向グラフ $G$ の任意の帰りがけ順序を考えます。前述の解析より、$\mathit{u.post} < \mathit{v.post}$ を満たす任意の辺 $u \rightarrow v$ に対して $G$ には $v$ から $u$ への有向路が含まれます。したがってもし $G$ が非巡回ならば、全ての辺 $u \rightarrow v$ に対して $\mathit{u.post} > \mathit{v.post}$ です。ここから任意の有向非巡回グラフ $G$ がトポロジカル順序を持つことが言えます。具体的には、$G$ の任意の帰りがけ順序を逆にしたものが $G$ のトポロジカル順序です。

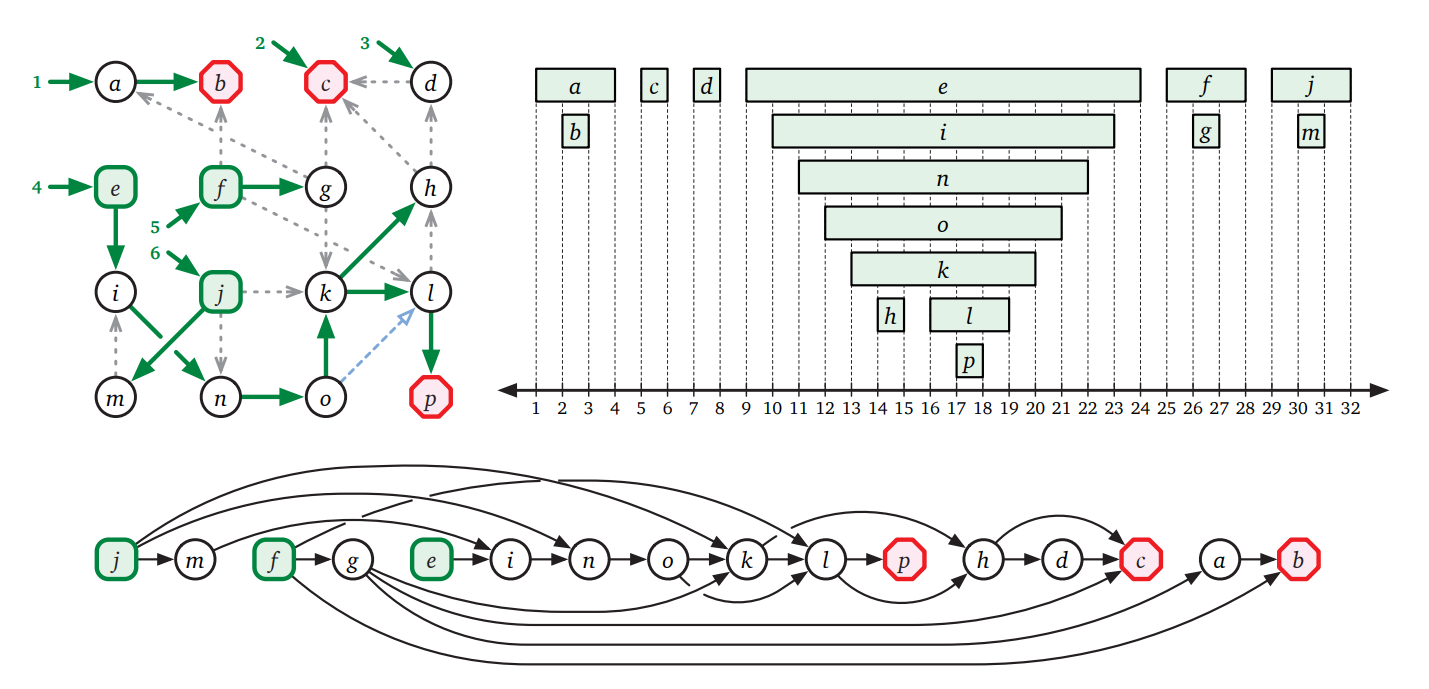
トポロジカル順序を別のデータ構造に書き出す必要があるなら、探索の途中で頂点をそのまま配列に書くことで $O(V+E)$ 時間で行えます:

procedure $\texttt{TopologicalSort}$($G$)

for 頂点 $v$ do

$\mathit{v.status} \leftarrow \textsc{New}$

$\color{red}{\mathit{clock} \leftarrow V}$

for 頂点 $v$ do

if $\mathit{v.status} = \textsc{New}$ then

${\color{red}{\mathit{clock}}} \leftarrow\,$$\texttt{TopSortDFS}$($v, \color{red}{\mathit{clock}}$)

return $\color{red}{S[1..V]}$

procedure $\texttt{TopSortDFS}$($v, \color{red}{\mathit{clock}}$)

$\mathit{v.status} \leftarrow \textsc{Active}$

for $v \rightarrow w$ の形をした辺 do

if $\mathit{w.status} = \textsc{New}$ then

${\color{red}{\mathit{clock}}} \leftarrow\,$$\texttt{TopSortDFS}$($w, \color{red}{\mathit{clock}}$)

$\mathit{v.status} \leftarrow \textsc{Finished}$

${\color{red}{S[\mathit{clock}]} \leftarrow v}$

${\color{red}{\mathit{clock}} \leftarrow \mathit{clock} - 1}$

return $\color{red}{\mathit{clock}}$

図 6.9

陽なトポロジカルソート

陰的なトポロジカルソート

しかしトポロジカル順序を別のデータ構造に格納するというのは多くの場合やりすぎです。トポロジカルソートの応用では頂点をトポロジカル順序に並べたリストが得たいのではなくて、トポロジカル順序 (あるいはその逆順) に沿って頂点ごとに何らかの計算を行いたい状況がほとんどであり、このような応用では、グラフのトポロジカル順序を記録する必要はありません！

有向非巡回グラフの頂点をトポロジカル順序の逆順で処理したいならば、頂点を再帰的深さ優先探索の最後で処理するようにすればそれで済みます。結局、トポロジカル順序とは帰りがけ順序の逆順なのですから！

procedure $\texttt{PostProcess}$($G$)

for 頂点 $v$ do

$\mathit{v.status} \leftarrow \textsc{New}$

for 頂点 $v$ do

if $\mathit{v.status} = \textsc{New}$ then

$\texttt{PostProcessDFS}$($v$)

procedure $\texttt{PostProcessDFS}$($v$)

$\mathit{v.status} \leftarrow \textsc{Active}$

for $v \rightarrow w$ の形をした辺 do

if $\mathit{w.status} = \textsc{New}$ then

$\texttt{PostProcessDFS}$($w$)

else if $\mathit{w.status} = \textsc{Active}$ then

エラーを出す

$\mathit{v.status} \leftarrow \textsc{Finished}$

$\texttt{Process}$($v$)

もし入力されるグラフが非巡回であることが事前に分かっているなら、頂点の状態を保存する代わりに印をつけるようしてこのアルゴリズムをさらに簡略化できます:

procedure $\texttt{PostProcessDag}$($G$)

for 頂点 $v$ do

$v$ の印を消す

for 頂点 $v$ do

if $v$ に印が付いていない then

$\texttt{PostProcessDagDFS}$($v$)

procedure $\texttt{PostProcessDagDFS}$($v$)

$v$ に印をつける

for $v \rightarrow w$ の形をした辺 do

if $w$ に印が付いていない then

$\texttt{PostProcessDFS}$($w$)

$\texttt{Process}$($v$)

これは一般的な深さ優先探索と全く同じで、 $\textsc{PostVisit}$ が $\textsc{Process}$ に変わっているだけです！

有向非巡回グラフに対する帰りがけ順の処理はとてもよく使われるので、私はこの処理を次のように省略して書くことがあります:

procedure $\texttt{PostProcessDAG}$($G$)

for 帰りがけ順の頂点 $v$ do

$\textsc{Process}(v)$

例えば先述の陽的なトポロジカルソートは次のように書けます:

procedure $\texttt{TopologicalSort}$($G$)

$\mathit{clock} \leftarrow V$

for 帰りがけ順の頂点 $v$ do

$S[\mathit{clock}] \leftarrow v$

$\mathit{clock} \leftarrow \mathit{clock} - 1$

return $S[1..V]$

DAG をトポロジカル順序通りに処理したい場合には、頂点をトポロジカル順序に配列に保存し、その配列に対して単純な for ループを回すことで行えます。順序を配列に書き出すことができない場合には、DAG $G$ の逆 (reversal) と呼ばれるグラフに対して深さ優先探索を行うことでも同じ処理を行えます。有向グラフ $G$ の逆とは $G$ の全ての辺 $u \rightarrow w$ を $u \leftarrow w$ に取り換えることで得られるグラフであり、$\mathit{rev}(G)$ と表されます。有向グラフ $G$ に含まれる閉路は $\mathit{rev}(G)$ でも閉路を作るので、DAG の逆は DAG です。$G$ におけるシンクは $\mathit{rev}(G)$ におけるソースとなります (逆も成り立ちます)。また $\mathit{rev}(G)$ におけるトポロジカル順序が $G$ のトポロジカル順序の逆順であることは帰納法によって示せます³。標準的な隣接リストで表された任意の有向グラフの逆は $O(V+E)$ で計算できます: 詳細は簡単な練習問題とします。

メモ化と動的計画法

トポロジカルソートを使うと多くの動的計画法のアルゴリズムを表現できます。ここでは例として依存グラフを考えます。以前触れた通り、再帰方程式の依存グラフ (dependency graph) とは、頂点が再帰的な小問題に対応する有向グラフであって、小問題同士を結ぶ辺があるのは始点の問題を解くときに終点の問題の答えが必要になるときだけであるものです。依存グラフに閉路があるとナイーブな再帰的アルゴリズムが停止しなくなるので、依存グラフは必ず非巡回です。

メモ化を使った再帰方程式の評価は依存グラフに対する深さ優先探索と全く同じです。具体的には、依存グラフの頂点に "印が付いている" ことが、その頂点の表す小問題の答えが計算されていることに対応し、ブラックボックスなサブルーチン $\textsc{PreVisit}$ と $\textsc{PostVisit}$ が実際の計算に対応します:

procedure $\texttt{Memoize}$($x$)

if $value[x]$ が未定義 then

$value[x]$ を初期化する

${}$

for $x$ が依存する小問題 $y$ do

$\texttt{Memoize}$($y$)

$value[y]$ で $value[x]$ を更新する

$value[x]$ の最終処理をする

procedure $\texttt{DFS}$($v$)

if $v$ に印が付いていない then

$v$ に印をつける

$\texttt{PreVisit}$($x$)

for 全ての辺 $v \rightarrow w$ do

$\texttt{DFS}$($w$)

${}$

$\texttt{PostVisit}$($x$)

図 6.10

メモ化再帰は深さ優先探索であり、深さ優先探索はメモ化再帰である

この対応関係についてさらに考えると、動的計画法を使った再帰方程式の評価が、依存グラフに対するトポロジカル順序の逆順の評価に対応することが分かります ――全ての小問題は依存する小問題が計算された後に計算されるからです。よって全ての動的計画法のアルゴリズムは、計算する再帰方程式の依存グラフの帰りがけ順走査に等しくなります！

procedure $\texttt{DynamicProgramming}$($G$)

for 帰りがけ順の小問題 $x$ do

$value[x]$ を初期化する

for $x$ が依存する小問題 $y$ do

$value[y]$ で $value[x]$ を更新する

$value[x]$ の最終処理をする

図 6.11

動的計画法は帰りがけ順の走査である

ただし動的計画法とトポロジカルソートの間には微妙な違いがあります。まず、ほとんどの動的計画法のアルゴリズムにおいて依存グラフは明示的に定義されません。つまり頂点と辺が実際にメモリ上に格納されるのではなく、再帰方程式によって陰に表されます。しかしある問題が依存する再帰的な小問題を定数時間で列挙できるという条件の下では依存グラフが存在するかのように処理を行えるので、実際のアルゴリズムがこの違いに大きく影響されることはありません。

もう一つのもっと重要な違いは、動的計画法の依存グラフのほとんどは構造化されているという点です。例えば五章で説明した編集距離問題に対する依存グラフは完全な格子に対角線が入ったものであり、最適二分探索木問題に対する依存グラフは直角三角形に右または上方向の辺が付いたものです。この周期的な構造のおかげで、動的計画法の依存グラフのトポロジカル順序 (の逆順) はネストされた for ループを使ってアルゴリズムの中に組み込むことができます。これまではこのトポロジカル順序のことを「破綻しない評価順序」と呼んでいました。

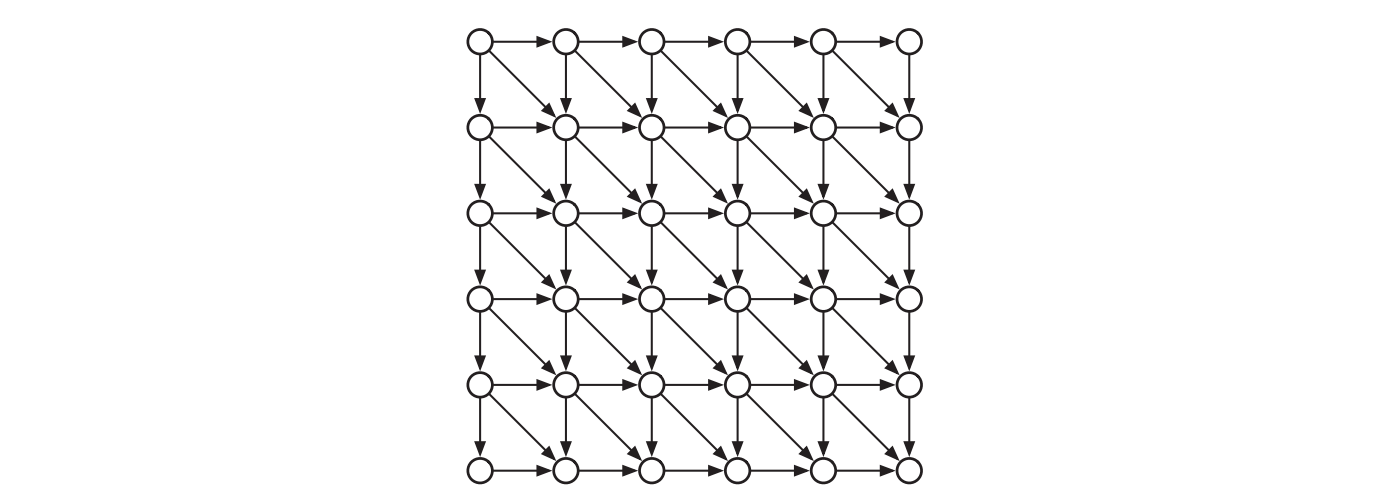
編集距離問題の再帰方程式に対する <strong>DAG</strong> — 図 6.12

編集距離問題の再帰方程式に対する **DAG**

DAG の上での動的計画法

逆に言えば、構造化されていない依存グラフを持つ問題に対する動的計画法のアルゴリズムを深さ優先探索を使って作ることができます。例として、辺が長さを持つ有向グラフ $G$ における頂点 $s$ から $t$ への有向路で長さが最大のものを求める最長路 (longest path) 問題を考えます。一般の有向グラフに対する最長路問題は巡回セールスマン問題からの簡単な帰着で NP 完全であることが示せますが、$G$ が非巡回の場合には線形時間の簡単な解法が存在します。

与えられた終点を $t$ とし、$v$ を任意の頂点とします。$G$ における $v$ から $t$ への最長路の長さを $LLP(v)$ とします。$G$ が DAG ならば、次の再帰方程式が成り立ちます: \[ LLP(v) = \begin{cases} 0 & \text{if } v = t \\ \max \lbrace l(v \rightarrow w) + LLP(w)\ |\ v \rightarrow w \in E \rbrace & \text{それ以外} \end{cases} \] ここで $l(v \rightarrow w)$ は辺 $v \rightarrow w$ の重み (ここでは"長さ") を表し、$\max \varnothing = - \infty$ です。例えば $v$ が $t$ と異なるシンク頂点なら $LLP(v) = -\infty$ です。

この再帰方程式に対する依存グラフは入力グラフ $G$ 自身です。なぜなら、小問題 $LLP(v)$ が $LLP(w)$ に依存することが辺 $v \rightarrow w$ が存在することと同値だからです。したがって頂点 $s$ から始まる $G$ の深さ優先探索を使えばこの再帰的関数を $O(V+E)$ 時間で評価できます。次のアルゴリズムは各頂点に対する最長の長さ $LLP(v)$ を追加のフィールド $LLP$ に保存します:

procedure $\texttt{LongestPath}$($v, t$)

if $v = t$ then

return 0

if $v.LLP$ が定義されていない then

$v.LLP \leftarrow - \infty$

for $v \rightarrow w$ の形をした辺 do

$v.LLP \leftarrow \max \lbrace v.LLP,\ l(v \leftarrow w) + \textsc{LongestPath}(w,t) \rbrace$

return $v.LLP$

今までに説明したことを使えば、このメモ化付き再帰的アルゴリズムをトポロジカルソートを使って書き直して、動的計画法のアルゴリズムを得ることができます。

procedure $\texttt{LongestPath}$($s, t$)

for 帰りがけ順の頂点 $v$ do

if $v = t$ then

$v.LLP \leftarrow 0$

else

$v.LLP \leftarrow - \infty$

for $v \rightarrow w$ の形をした辺 do

$v.LLP \leftarrow \max \lbrace v.LLP,\ l(v \rightarrow w) + w.LLP \rbrace$

return $s.LLP$

二つのアルゴリズムは同一と言ってもよいでしょう ――最初のアルゴリズムにおける再帰と、二つ目のアルゴリズムにおける for ループが "同じ" 深さ優先探索を表すのです！どちらを選ぶかは完全に好みの問題です。

動的計画法の問題のうち最適な決断の列 (decision sequence) を作るものはほとんど常に、特定の DAG における最適路を見つける問題に置き換えることができます。例えば二章と三章で扱った文字列分割、部分和、最長増加部分列、編集距離の問題は全て、頂点や辺に重みの付いた DAG において最長または最小の路を見つける問題に変形でき、その DAG とは元の問題の依存グラフです。一方で最適二分探索木や木の最大独立集合を見つける問題のような、"木の形をした" 動的計画法の問題は、DAG における最適路を見つける問題に変形できません。

強連結性

有向グラフにおける連結性の正式な定義に戻りましょう。有向グラフ $G$ の頂点 $u$ が他の頂点 $v$ に到達するとは、$G$ に $u$ から $v$ への有向路があることを言い、$\mathit{reach}(u)$ で $u$ から到達できる頂点全体の集合を表しました。二つの頂点 $u, v$ が強連結 (strongly connected) であるとは、$u$ が $v$ に到達し、かつ $v$ が $u$ に到達することを言います。有向グラフが強連結であるとは全ての頂点の組が強連結であることと同値です。

定義をうんざりするほどこねくり回すと、任意の有向グラフにおける強連結性が (無向グラフに対する接続性と同じように) 頂点集合に対する同値関係であることが示せます。この同値関係の同値類を、$G$ の強連結成分 (strongly connected component) あるいはもっと単純に強線分 (strong component) と呼びます。同じことを言い換えると、$G$ の強連結成分は $G$ の極大な強連結部分グラフです。有向グラフ $G$ が強連結であることは、$G$ がちょうど一つの強連結成分を持つことと同値です。もう一方の極を考えると、有向グラフ $G$ が DAG であることは $G$ の全ての強連結成分が一つの頂点からなることと同値です。

強連結成分グラフ (strong component graph) $\mathit{scc}(G)$ とは $G$ の強連結成分を一つの頂点にまとめ、強連結成分の間の辺を一つに束ねることで得られる有向グラフのことです (強連結成分グラフはメタグラフ (meta-graph) あるいは凝縮グラフ (condensation graph) とも呼ばれます)。$\mathit{scc}(G)$ が必ず DAG であることを示すのは難しくない (ヒント、ヒント) ので、少なくとも理論上は $G$ の強連結成分をトポロジカル順序に並べられます。つまり、全ての頂点を一列に並べて全ての後方辺が同じ強連結成分にある頂点を結ぶようにできるということです。

図 6.13

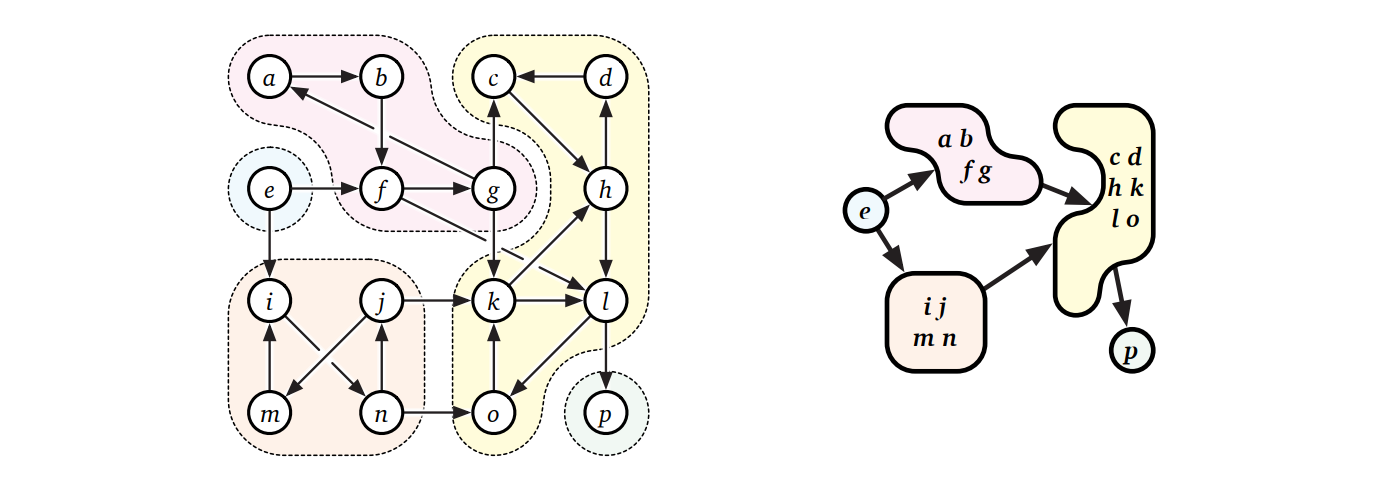
グラフ $G$ の強連結成分と強連結成分グラフ $\mathit{scc}(G)$

一つの頂点が属する強連結成分を $O(V+E)$ で計算するのは簡単です。まず何か優先探索で $\mathit{reach}(v)$ を計算し、次に $G$ の逆を探索することで $\mathit{reach}^{-1}(v) =$ $\lbrace u\ |\ v \in \mathit{reach}(u) \rbrace$ を計算します。こうすれば、 $v$ の強連結成分は二つの集合の交差 $\mathit{reach}(v) \cap \mathit{reach}^{-1}(v)$ となります。このアルゴリズムを使えば、グラフ全体が強連結かどうかを $O(V + E)$ 時間で判定できます。

同様に、このアルゴリズムを標準的なラッパー関数で包めば有向グラフの全ての強連結成分の計算できます。ただし、こうして出来上がるアルゴリズムの実行時間はグラフが DAG であったとしても $O(VE)$ です: 強連結成分は最大で $V$ 個あり、一つを計算するのに $O(E)$ 時間かかるからです。もちろんこれは改善できます！前述の通り、全ての強連結成分が一つの頂点からなるかどうかは (深さ優先探索を使って) $O(V + E)$ 時間で判定できるのですから。

線形時間で強連結成分を求める

有向グラフの強連結成分を $O(V+E)$ 時間で計算するアルゴリズムはいくつかありますが、どれも突き詰めれば次の観察に基づいています:

命題 6.2 任意の有向グラフ $G$ の深さ優先走査を一つ固定する。$G$ の任意の強連結成分 $C$ には $C$ の中に親を含まない頂点がちょうど一つ含まれる (この頂点の親は他の強連結成分に含まれるか、そうでなければ親を持たない)。

証明 $G$ の任意の強連結成分を $C$ とする。適当な頂点 $v \in C$ から $w \in C$ への任意の路を考える。この路上の全ての頂点は $w$ に到達でき、したがって $C$ の全ての頂点に到達できる。対称的に、この路上の全ての頂点は $v$ から到達でき、したがって $C$ の全ての頂点から到達できる。よってこの路上の全ての頂点も $C$ に属する。

$v$ を $C$ の中で一番早い開始時間を持つ頂点とする。$v$ の親 $\mathit{parent}(v)$ は $v$ よりも早く始まっているので $C$ に属さない。

$w$ を $C$ に属する $v$ と異なる頂点とする。 $\textsc{DFS}(v)$ が呼ばれる直前、$C$ の全ての頂点は未処理だから、未処理の頂点だけを通る $v$ から $w$ への路が存在する。命題 6.1より、深さ優先森において $w$ は $v$ の子孫である。よって木辺だけからなる $v$ から $w$ への路に含まれる頂点は全て $C$ に含まれる。特に $\mathit{parent}(w) \in C$ である。 $\Box$

この命題を使えば、有向グラフ $G$ の各強連結成分が $G$ の深さ優先探索森の連結部分木を定義することが示せます。具体的には各強連結成分 $C$ について、 $C$ の中で開始時間の最も早い頂点が $C$ の全ての頂点を子孫として持つ最も低い頂点 ($C$ の頂点の lowest common ancestor) となります。この頂点のことをこれから $C$ の根 (root) と呼びます。

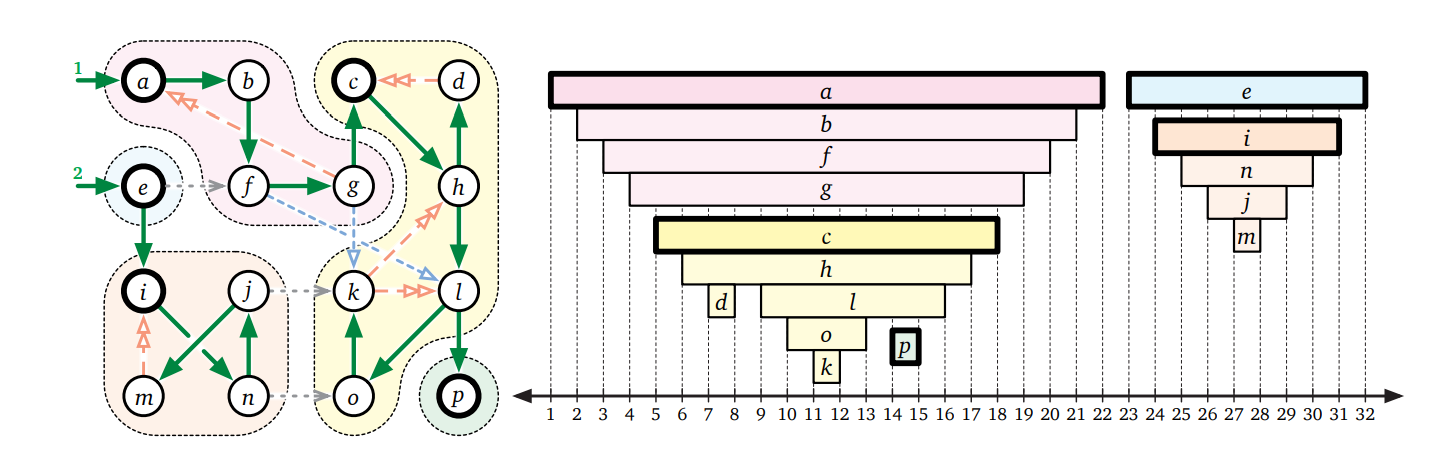
これから二つのアルゴリズムを示しますが、どちらもここに示す観察に基づいています: $G$ の強連結成分 $C$ であって $\mathit{scc}(G)$ でシンクであるものを考えます。このような $C$ をシンク成分 (sink component) と呼びます。同じことですが、$C$ がシンク成分なのは $C$ に含まれる頂点から到達できる頂点の集合が $C$ と同じときです。$G$ のシンク成分に含まれる頂点 $v$ を (何らかの方法で) 見つけることができれば、それを繰り返すことで $G$ の全ての強連結成分を計算できます。つまり、$v$ を見つけ、$v$ から到達できる頂点の集合 (シンク成分) を計算し、シンク成分をグラフから消すという処理を頂点が無くなるまで繰り返すということです。シンク成分に含まれる頂点を見つける方法が分からないので、この説明をアルゴリズムと呼ぶことはできませんが！

procedure $\texttt{StrongComponents}$($G$)

$count \leftarrow 0$

while $G$ が空でない do

$C \leftarrow \varnothing$

$count \leftarrow count + 1$

$\color{red}{v \leftarrow G}$ のシンク成分に含まれる適当な頂点 $\quad$ ⟨⟨マジック！⟩⟩

for $\mathit{reach}(v)$ に含まれる頂点 $w$ do

$\mathit{w.label} \leftarrow count$

$w$ を $C$ に加える

$C$ と $C$ に向かう辺を $G$ から削除する

図 6.15

強連結成分を計算するアルゴリズムに極めて近い何か

Kosaraju と Sharir のアルゴリズム

一目見ただけでは、グラフのシンク成分に含まれる頂点を素早く見つけるというのはとても難しく思えます。しかし、グラフのソース成分 ――$\mathit{scc}(G)$ におけるソースに対応する $G$ の強連結成分―― に含まれる頂点を見つけるという正反対の問題なら、実は深さ優先探索を使ってとても簡単に解くことができます。

命題 6.3 $G$ の帰りがけ順序で最後に来る頂点は $G$ のソース成分に含まれる。

証明適当な $G$ の深さ優先走査を固定し、その帰りがけ順序で最後に来る頂点を $v$ とする。このとき $\textsc{DFS}(v)$ という呼び出しはラッパーアルゴリズム $\textsc{DFSAll}$ が行う最後の $\textsc{DFS}$ 関数の呼び出しである。さらに $v$ は深さ優先全域木森の根だから、$\mathit{v.pre} < \mathit{x.post}$ を満たす任意の頂点 $x$ は $v$ の子孫である。そして、$v$ は自身が属する強連結成分 $C$ の根である。

背理法を使って、$x \notin C$ かつ $y \in C$ である辺 $x \rightarrow y$ が存在しないことを示す。$x \notin C$ かつ $y \in C$ である辺 $x \rightarrow y$ が存在すると仮定する。このとき $x$ は $y$ に到達でき、かつ $y$ は $v$ に到達できるので、$x$ は $v$ に到達できる。$v$ は $C$ の根であることから $y$ は $v$ の子孫であり、よって $\mathit{v.pre} < \mathit{y.pre}$ である。加えて辺 $x \rightarrow y$ の存在より $\mathit{y.pre} < \mathit{x.post}$ が言えるので、$\mathit{v.pre} < \mathit{x.post}$ が分かる。したがって $x$ は $v$ の子孫となるが、このとき $v$ は (木辺をたどって) $x$ に到達できるので $x \in C$ であり、 $x \notin C$ という仮定と矛盾する。 $\Box$

任意の有向グラフ $G$ に対して $\mathit{rev}(\mathit{scc}(G)) = \mathit{scc}(\mathit{rev}(G))$ となることは簡単に確認できる (ヒント、ヒント) ので、 $\mathit{rev}(G)$ の帰りがけ順序で最後の頂点が元のグラフ $G$ のシンク成分に含まれます。したがって、$\mathit{rev}(G)$ の帰りがけ順に頂点をたどるラッパー関数を使って二回目の走査を行えば、$\textsc{DFS}$ の各呼び出しはちょうど一つの $G$ の強連結成分を訪れます⁴。

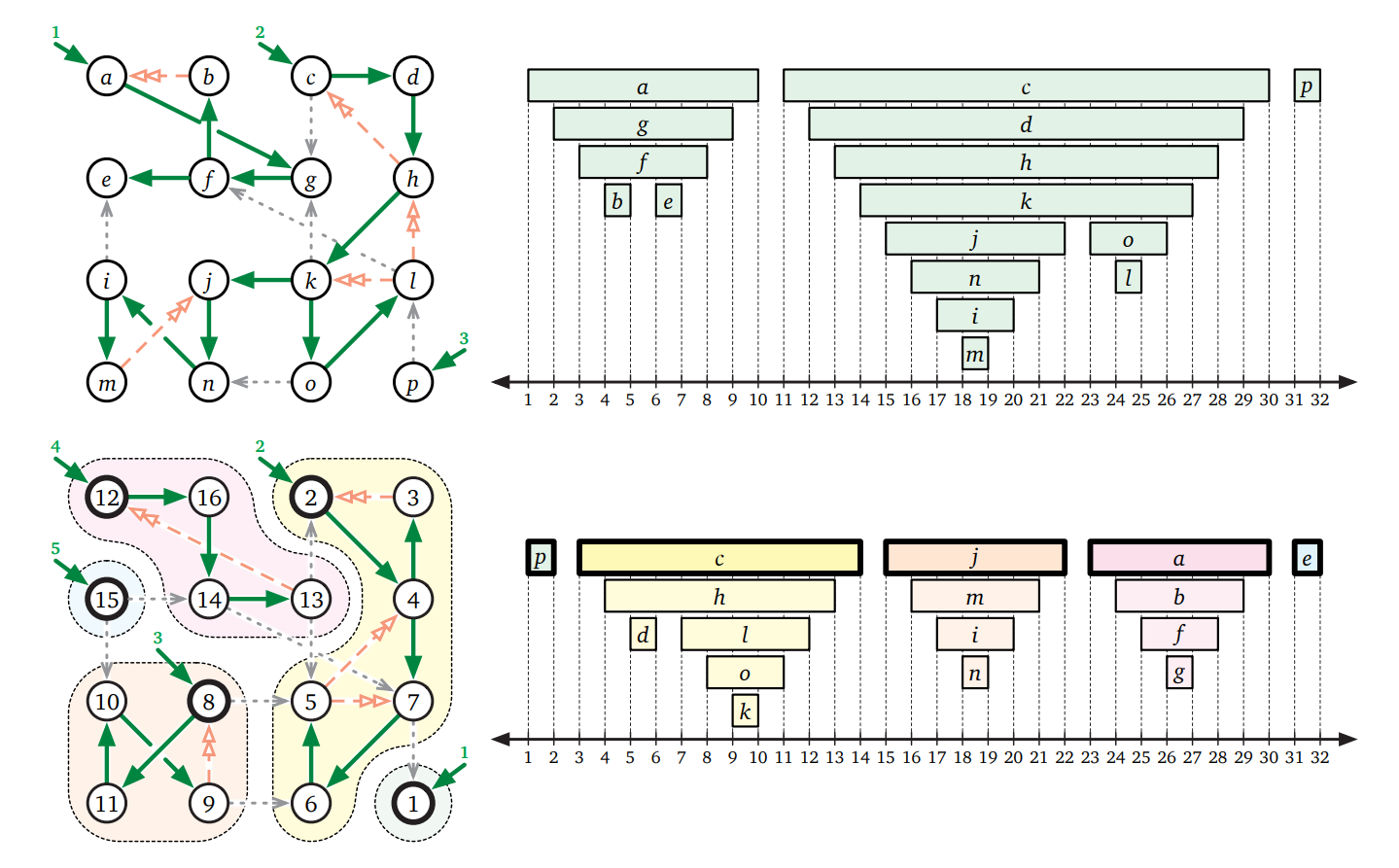
全てまとめると、次に示すアルゴリズムを得ます。このアルゴリズムは任意の有向グラフの強連結成分の数を数え、頂点を強連結成分の番号でラベル付けするという処理を $O(V+E)$ 時間で行います。このアルゴリズムは 1978 年に Rao Kosaraju (ラオ・コサラジュ) によって発見され (しかし公表はされず)、その後 1981 年⁵に Micha Sharir (ミカ・シャリア) によって独立に発見されました。Kosaraju-Sharir のアルゴリズムは二つのフェーズからなります。一つ目のフェーズは $\mathit{rev}(G)$ に対する深さ優先探索であり、探索が終わった頂点を順にスタックに積んでいきます。二つ目のフェーズは元のグラフ $G$ に対する何か優先探索であり、この探索はフェーズ 1 でスタックに積んだ頂点をポップしながら行います。このアルゴリズムは (二回目の深さ優先探索で) 各頂点を強連結成分の根でラベル付けします。

procedure $\texttt{KosarajuSharir}$($G$)

$S \leftarrow$ 空のスタック

for 頂点 $v$ do

$v$ の印を消す

$\mathit{v.root} \leftarrow \textsc{None}$

⟨⟨フェーズ 1: $\mathit{rev}(G)$ の帰りがけ順にプッシュする⟩⟩

for 頂点 $v$ do

if $v$ に印が付いていない then

$\texttt{PushPostRevDFS}$($v, S$)

⟨⟨フェーズ 2: スタックの順番に $G$ をもう一度 $\textsc{DFS}$ する⟩⟩

while $S$ が空でない do

$\color{#2D2F91}{v \leftarrow \textsc{Pop}(S)}$

if $\mathit{v.root} = \textsc{None}$ then

$\texttt{LabelOneDFS}$($v, v$)

procedure $\texttt{PushPostRevDFS}$($v, S$)

$v$ に印をつける

for $u \rightarrow v$ の形をした辺 ⟨⟨逆！⟩⟩ do

if $u$ に印が付いていない then

$\texttt{PushPostRevDFS}$($u, S$)

$\color{#2D2F91}{\textsc{Push}(v, S)}$

procedure $\texttt{LabelOneDFS}$($v, r$)

$\mathit{v.root} \leftarrow r$

for $v \rightarrow w$ の形をした辺 do

if $\mathit{w.root} = \textsc{None}$ then

$\texttt{LabelOneDFS}$($w, r$)

図 6.16

Kosaraju-Sharir の強連結成分アルゴリズム

Kosaraju-Sharir のアルゴリズムをこれまで使ってきた例のグラフに適用した様子を次の図に示します。このアルゴリズムをほんの少し変更すれば、強連結成分グラフ $\mathit{scc}(G)$ を $O(V+E)$ 時間で計算するアルゴリズムを得ることができます。

図 6.17

Kosaraju-Sharir のアルゴリズムの実行例。上: 逆グラフの深さ優先探索。下: 最初の走査で計算した帰りがけ順の逆順に根の頂点を訪ねながら行う深さ優先探索。

❤ Tarjan のアルゴリズム

1972 年⁶に Bob Tarjan (ボブ・タージャン) によって発表された強連結成分を計算する線形時間アルゴリズムは、Kosaraju-Sharir のアルゴリズムよりも早く発見されていますが、はるかに細かなテクニックを使います。直感的に説明すると、Tarjan のアルゴリズムは $G$ のソース成分を見つけ、"削除" し、"再帰的に" 残りの強連結成分を見つけます。そして重要なのが、この計算全体が一回の深さ優先探索で行われる点です。

有向グラフ $G$ の適当な深さ優先探索を固定します。各頂点 $v$ について、$v$ から木辺のみをたどって到達できる頂点からさらに一つ以下の木辺でない辺をたどって到達できる頂点の開始時間の中で最速のものを $\pmb{\mathit{low}(v)}$ で表すことにします。この定義から自明に分かることとして、$\mathit{low}(v) \leq \mathit{v.pre}$ です。なぜなら $v$ はゼロ個の木辺とゼロ個の木辺でない辺をたどることで $v$ から到達できる頂点だからです。Tarjan はこの $\mathit{low}$ 関数を使ったシンク成分の特徴付けを発見しました。

命題 6.4 頂点 $v$ が $G$ のシンク成分の根であることは、$\mathit{low}(v) = \mathit{v.pre}$ かつ $v$ の全ての真の子孫 $w$ について $\mathit{low}(w) < \mathit{w.pre}$ であることと同値である。

証明まず $\mathit{low}(v) = \mathit{v.pre}$ が成り立つ $v$ を選ぶ。$\mathit{low}(v) = \mathit{v.pre}$ より、$w$ を $v$ の任意の子孫とすると、辺 $w \rightarrow x$ であって $\mathit{x.pre} < \mathit{v.pre}$ が成り立つものは存在しない。一方で何か優先探索の定義より $\mathit{y.pre} > \mathit{v.post}$ を満たす頂点 $y$ には $v$ から到達できない。よって $v$ から到達できるのは $v$ の深さ優先探索森における子孫だけであり、$v$ の子孫が到達できるのは $v$ の子孫だけと分かる。加えて $v$ に親が存在したとしても到達できないので、$v$ は強連結成分の根である。

これに加えて $v$ の全ての真の子孫 $w$ に対して $\mathit{low}(w) < \mathit{w.pre}$ が成り立つとする。このとき、全ての $v$ の子孫 $w$ に対して、$w$ が到達できる (同じく $v$ の子孫である) 頂点 $x$ で $\mathit{x.pre} < \mathit{w.pre}$ を満たすものが存在する。よって帰納法により $v$ の任意の子孫は $v$ に到達できることが分かる。したがって $v$ の子孫は $v$ が根であるような強連結成分 $C$ を構成する。さらに $v$ からは $C$ でない頂点に到達できないことから、$C$ はシンク成分である。

逆に $v$ がシンク成分 $C$ の根であると仮定する。このとき $v$ が $w$ に到達できることは $w \in C$ と同値である。$v$ は $v$ の子孫全てに到達でき、$C$ に含まれる頂点は $v$ の子孫であるから、$v$ の子孫がちょうど $C$ となる。もしある $w \in C$ に対して $\mathit{low}(w) = \mathit{w.pre}$ ならば $w$ が $C$ のもう一つの根となるが、そんなことはあり得ない。 $\Box$

頂点 $w$ に対する $\mathit{low}(w)$ の計算は深さ優先探索を使って素直に行えます:

procedure $\texttt{FindLow}$($G$)

$\mathit{clock} \leftarrow 0$

for 頂点 $v$ do

$v$ の印を消す

for 頂点 $v$ do

if $v$ に印が付いていない then

$\texttt{FindLowDFS}$($v$)

procedure $\texttt{FindLowDFS}$($v$)

$v$ に印をつける

$\mathit{clock} \leftarrow \mathit{clock} + 1$

$\mathit{v.pre} \leftarrow \mathit{clock}$

$\mathit{v.low} \leftarrow \mathit{v.pre}$

for $v \rightarrow w$ の形をした辺 do

if $w$ に印が付いていない then

$\texttt{FindLowDFS}$($w$)

$\mathit{v.low} \leftarrow \min \lbrace \mathit{v.low},\ \mathit{w.low} \rbrace$

else

$\mathit{v.low} \leftarrow \min \lbrace \mathit{v.low},\ \mathit{w.pre} \rbrace$

図 6.18

各頂点 $v$ に対する $\mathit{low}(v)$ の計算

命題 6.4から、$\textsc{FindLow}$ 実行した後にグラフ全体に対する何か優先探索を行うことで全てのシンク成分の根を $O(V + E)$ 時間で計算できます。その後シンク成分に印をつけて削除するのは (根から始まる何か優先探索で) $O(V+E)$ 時間で行えます。以上の処理を再帰的に行えば強連結成分を計算できますが、残念ながらこのアルゴリズムでは反復ごとに頂点を一つしか取り除けない可能性があります。その場合反復が最大で $V$ 回行われるため、このナイーブなアルゴリズムの実行時間は $O(VE)$ となってしまいます。

この戦略を高速化するために、Tarjan のアルゴリズムは頂点のスタックを (再帰スタックとは別に) 管理します。新しい頂点の探索を始めるときに頂点をスタックにプッシュしていき、頂点 $v$ の探索が終わるたびに $\mathit{v.low}$ と $\mathit{v.pre}$ を比較します。初めて $\mathit{v.low} = \mathit{v.pre}$ となったとき、次の三つの条件が成り立ちます:

$v$ はシンク成分 $C$ の根である。
$C$ に含まれる頂点はスタックの頂上から連続して積まれている。
スタックの一番深くに積まれている $C$ の頂点は $v$ である。

よってスタックを $v$ が出てくるまでポップすれば、この時点で $C$ の頂点を特定できます。

特定した $C$ の頂点をグラフから削除して残りのグラフの強連結成分を再帰的に計算することもできますが、こうすると $v$ から始まる同じ探索をもう一度行うことになるので無駄があります。その代わり、$C$ の各頂点に強連結成分の根が $v$ であることを示すラベルを付け、それらの頂点を以降の深さ優先探索で無視するようにします。きちんと言うと、探索をこう改変することで、$\mathit{low}(v)$ の定義が「$v$ から木辺のみをたどって到達できる頂点からさらに一つ以下の木辺でない辺をたどって到達できる $\pmb{v}$ と同じ強連結成分に属する頂点の開始時間の中で最速のもの」となります。ただしアルゴリズムの正しさを証明するには、ラベルの付いた頂点を無視したときと実際にそれらの頂点を削除したときのアルゴリズムの振る舞いが同じことを示すだけで済みます。

これでようやく Tarjan のアルゴリズムを示せます。$\textsc{FindLow}$ からの変更を赤字で示します。アルゴリズムは二つの部分に分かれます。一つは各頂点が一回ずつスタック $S$ にプッシュおよびポップされる部分で、実行時間は $O(V)$ です。残りは標準的な深さ優先探索で、実行時間は $O(V+E)$ です。したがって、アルゴリズム全体の実行時間は $\pmb{O(V+E)}$ となります。

procedure $\texttt{Tarjan}$($G$)

$\mathit{clock} \leftarrow 0$

$S \leftarrow$ 新しい空のスタック

for 頂点 $v$ do

$v$ の印を消す

$\mathit{v.root} \leftarrow \textsc{None}$

for 頂点 $v$ do

if $v$ に印が付いていない then

$\texttt{TarjanDFS}$($v$)

procedure $\texttt{TarjanDFS}$($v$)

$v$ に印をつける

$\mathit{clock} \leftarrow \mathit{clock} + 1$

$\mathit{v.pre} \leftarrow \mathit{clock}$

$\mathit{v.low} \leftarrow \mathit{v.pre}$

$\color{red}{\textsc{Push}(S, v)}$

for $v \rightarrow w$ の形をした辺 do

if $w$ に印が付いていない then

$\texttt{FindLowDFS}$($w$)

$\mathit{v.low} \leftarrow \min \lbrace \mathit{v.low},\ \mathit{w.low} \rbrace$

else if $\color{red}{\mathit{w.root} = \textsc{None}}$ then

$\mathit{v.low} \leftarrow \min \lbrace \mathit{v.low},\ \mathit{w.pre} \rbrace$

if $\color{red}{\mathit{v.low} = \mathit{v.pre}}$ then

$\color{red}{w \leftarrow \textsc{Pop(S)}}$

while $\color{red}{w \neq v}$ do

$\color{red}{\mathit{w.root} \leftarrow v}$

$\color{red}{w \leftarrow \textsc{Pop}(S)}$

$\color{red}{\mathit{w.root} \leftarrow v}$

図 6.19

Tarjan の強連結成分アルゴリズム

練習問題

深さ優先探索・トポロジカルソート・強連結成分

1. 有向グラフ $G$ の逆 $\mathit{rev}(G)$ を $O(V+E)$ 時間で計算するアルゴリズムを説明してください。
2. 任意の有向グラフ $G$ について、強連結成分グラフ $\mathit{scc}(G)$ が非巡回であることを示してください。
3. 任意の有向グラフ $G$ について、$\mathit{scc}(\mathit{rev}(G)) = \mathit{rev}(\mathit{scc}(G))$ を示してください。
4. 有向グラフ $G$ を固定します。$G$ の任意の頂点 $v$ について、$S(v)$ で $v$ を含む $G$ の強連結成分を表すことにします。$G$ の任意の頂点 $u, v$ について、$G$ において $v$ が $u$ に到達可能なことと $\mathit{scc}(G)$ において $S(v)$ が $S(u)$ に到達可能なことが同値だと示してください。
5. 有向グラフ $G$ の二つの強連結成分を $S, T$ とします。任意の $u \in S$ と $v \in T$ に対して $\mathit{finish}(u) < \mathit{finish}(v)$ であるか、そうでなければ任意の $u \in S$ と $v \in T$ に対して $\mathit{finish}(u) > \mathit{finish}(v)$ であることを示してください。
有向グラフ $G$ が半接続 (semi-connected) であるとは、任意の頂点の組 $u, v$ について、$u$ が $v$ に到達可能であるか $v$ が $u$ に到達可能なことを言います (両方向に到達可能でも構いません)。
1. ソース頂点を一つだけ持つ DAG であって半接続でないものの例を一つ示してください。
2. 与えられた有向非巡回グラフが半接続かどうかを判定するアルゴリズムを説明、解析してください。
3. 制約のない任意の有向グラフが半接続かどうかを判定するアルゴリズムを説明、解析してください。
Sham-Poobanana 市警察署は市内全ての道路を一方通行にすることを決定しました。自動車を運転する人が困惑しきって大勢文句を言ったにもかかわらず、市長は Sham-Poobanana 市内の任意の交差点の間は合法的に行き来できると言って聞きません。
1. 市は市長の主張を検証または反証しなければなりません。この問題をグラフの問題として定式化し、その問題を解くアルゴリズムを説明、解析してください。
2. (a) のアルゴリズムを実行したところ、市長は ~~嘘をついていた~~ 情報が間違って伝わっていたことを渋々認めました。市長がこの暴露を受けて主張したことによると、 Sham-Poobanana 市内の交差点のうち 95 % 以上は良い交差点であるとのことです。交差点 $x$ が良いとは、$x$ から到達できる全ての交差点 $y$ について $y$ から $x$ に到達できることを言います。彼女の主張を検証または反証する効率の良いアルゴリズムを説明、解析してください。
満点のためには、両方のアルゴリズムが線形時間で実行できることが求められます。
有向非巡回グラフ $G$ が唯一のソース $s$ と唯一のシンク $t$ を持つとします。頂点 $v \notin \lbrace s, t \rbrace$ が $\pmb{(s, t)}$-切断点であるとは、$s$ から $t$ への任意の路が $v$ を通ることを言います。同じことを言い換えると、$v$ を削除すると $s$ から $v$ に到達できなくなるならば $v$ は $(s,t)$-切断点です。$G$ の $(s,t)$-切断点を全て見つけるアルゴリズムを説明してください。

$三つの $(s,t)$-切断頂点を持つ DAG$

図 6.20

三つの $(s,t)$-切断頂点を持つ DAG
連結無向グラフ $G$ の頂点 $v$ が切断点 (cut vertex) であるとは、部分グラフ $G - v$ ($G$ から $v$ を取り除いて得られるグラフ) が非連結であることを言います。

図 6.21

四つの切断点を持つ無向グラフ
1. グラフ $G$ と頂点 $v$ が与えられたときに、$v$ が切断点であるかを判定する線形時間アルゴリズムを説明してください。全ての頂点に対してそのアルゴリズムを試した場合、全ての切断点を見つけるのにどれだけ時間がかかりますか？
2. 無向グラフ $G$ の深さ優先全域木を $T$ とします。
  1. $T$ の根が $G$ の切断点であるのはその根が $T$ で二つ以上の子を持つときに限ることを示してください。
  2. 根でない頂点 $v$ が $G$ の切断点であるのは、$v$ の ($T$ における) 子の ($T$ における) 子孫が $v$ の ($T$ における) 真の先祖に ($G$ で) 隣接するときに限ることを示してください。
  [ヒント: $T$ が深さ優先探索探索木でなかったり、$G$ が有向グラフであったりするとこれらの命題は成り立たなくなります。]
3. 無向グラフに含まれる全ての切断点を $O(V + E)$ 時間で見つけるアルゴリズムを説明してください。
連結無向グラフ $G$ の辺 $e$ が切断辺であるとは、部分グラフ $G - e$ ($G$ から $e$ を取り除いて得られるグラフ) が非連結であることを言います。
1. グラフ $G$ と頂点 $e$ が与えられたときに、$e$ が切断辺であるかを判定する線形時間アルゴリズムを説明してください。全ての辺に対してそのアルゴリズムを試した場合、全ての切断辺を見つけるのにどれだけ時間がかかりますか？
2. $G$ の任意の全域木を $T$ とします。$G$ の切断辺が $T$ の切断辺でもあることを示してください。この命題から、$G$ の切断辺は最大でも $V-1$ 本であることが分かります。(a) で答えた全ての切断辺を見つけるアルゴリズムはこの情報によってどの程度改善されますか？
3. $T$ の根を適当な頂点 $r$ に固定したとします。各頂点 $v$ について、$T_{v}$ で $v$ を根とする $T$ の部分木を表すことにします。例えば $T_{r} = T$ です。$uv$ を $T$ の任意の辺とし、$u$ が $v$ の親であるとします。$uv$ が $G$ の切断辺であるのは $G$ の辺で端点のちょうど片方が $T_{v}$ に属する唯一の辺が $uv$ である場合に限ることを示してください。
4. $G$ に含まれる全ての切断辺を見つける線形時間アルゴリズムを説明してください。 [ヒント: $G$ の深さ優先探索木を $T$ とします。]
有向グラフ $G$ の推移閉包 (transitive closure) $G^{T}$ とは $G$ と同じ頂点を持つグラフであって、辺 $u \rightarrow v$ が存在するのが $G$ に $u$ から $v$ への有向路が存在するときに限るものです。$G$ の推移縮約 (transitive reduction) とは推移閉包が $G^{T}$ と等しくなる最小の辺の集合です。グラフに対する推移縮約は一つだけとは限りません。
1. 与えられた有向グラフの推移閉包を効率良く計算するアルゴリズムを説明してください。
2. 有向グラフ $G$ の推移縮約が唯一であるのは $G$ が非巡回な場合に限ることを示してください。
3. 与えられた有向グラフの推移縮約を効率良く計算するアルゴリズムを説明してください。
任意の接続グラフに適用できる最も古いアルゴリズムの一つは、1895 年に Gaston Tarry (ガストン・タリー) によって迷路を解くために提案されました。Tarry のアルゴリズムに対する入力は無向グラフ $G$ ですが、表現を簡単にするために辺 $uv$ を二つの有向辺 $u \rightarrow v$ と $v \rightarrow u$ に分割します。(実際のプログラムにはこの分割に対応する処理は存在しません。アルゴリズムは与えられた $G$ の隣接リストが有向であると思って処理を行うだけです)。

くだけて説明すると、Tarry のアルゴリズムは頂点 $v$ を "訪れる" たびに $v$ に印を付け、$v \rightarrow w$ を赤く塗って $\textsc{RecTarry}(w)$ を呼ぶことで "走査" を行います。これまでに見たグラフの走査アルゴリズムと違って、Tarry のアルゴリズムは同じ頂点に複数回印を付けることがあります。

procedure $\texttt{Tarry}$($G$)

$G$ の全ての頂点の印を消す

$G$ の全ての辺を白く塗る

$s \leftarrow G$ の適当な頂点

$\texttt{RecTarry}$($s$)

procedure $\texttt{RecTarry}$($v$)

⟨⟨$v$ を訪れる⟩⟩

$v$ に印をつける $\quad$

if 白い辺 $v \rightarrow w$ がある then

if $w$ に印が付いていない then

$w \rightarrow v$ を緑色に塗る

⟨⟨$v \rightarrow w$ を走査する⟩⟩

$v \rightarrow w$ を赤色に塗る

$\texttt{RecTarry}$($w$)

else if 緑色の辺 $v \rightarrow w$ がある then

⟨⟨$v \rightarrow w$ を走査する⟩⟩

$v \rightarrow w$ を赤色に塗る

$\texttt{RecTarry}$($w$)
1. $O(V+E)$ 時間で動作する Tarry のアルゴリズムの実装を説明してください。
2. 二回以上走査される $G$ の有向辺が存在しないことを示してください。
3. このアルゴリズムが頂点 $v$ を $k$ 回目に訪れたとき、$v$ に向かう赤い辺と $v$ から出る赤い辺はそれぞれ何本ですか？ [ヒント: 開始頂点 $s$ とそれ以外の頂点を分けて考えてください。]
4. このアルゴリズムが開始頂点 $s$ 以外の頂点 $v$ を最大でも $\deg (v)$ 回訪れることを示してください。なお開始頂点では最大 $\deg(s) + 1$ 回となります。このことから $\textsc{Tarry}(G)$ が停止することが直ちに分かります。
5. $\textsc{Tarry}(G)$ が最後に訪れる頂点は開始頂点 $s$ であることを示してください。
6. $\textsc{Tarry}(G)$ が終了したとき、 $\textsc{Tarry}(G)$ が訪れる全ての頂点 $v$ について、 $v$ に向かう辺と $v$ から出る辺が全て赤いことを示してください。 [ヒント: 開始頂点 $s$ から始まる最初に頂点に印が付く順番を考え、帰納法を使います。]
7. $\textsc{Tarry}(G)$ が $G$ の全ての頂点を訪れることを示してください。これと前問の主張を組み合わせると、$\textsc{Tarry}(G)$ が $G$ の全ての辺をちょうど一回ずつ走査することが分かります。
Tarry のグラフ走査アルゴリズムの次の変種を考えます。ここでは緑色の辺を走査してもその辺を赤く塗り直すことはせず、その代わり各頂点に二つの数値を割り振ります:

次の主張を証明または反証してください: 「$\textsc{Tarry2}(G)$ が停止したとき、緑色の辺は全域木を定義し、 $\mathit{v.pre}$ と $\mathit{v.post}$ のラベルはそれぞれ行きがけ順および帰りがけ順のラベルであり、全て $G$ のある深さ優先探索で得られるものと等しい」言い換えると、$\textsc{Tarry2}(G)$ が辺を訪れる順番は深さ優先探索と全く違うにもかかわらず、出力が深さ優先探索と同じであることを証明または反証してください。

procedure $\texttt{Tarry2}$($G$)

$G$ の全ての頂点の印を消す

$G$ の全ての辺を白く塗る

$s \leftarrow G$ の適当な頂点

$\texttt{RecTarry2}$($s, 1$)

procedure $\texttt{RecTarry2}$($v, \mathit{clock}$)

if $v$ に印が付いていない then

$\mathit{v.pre} \leftarrow \mathit{clock};\ \mathit{clock} \leftarrow \mathit{clock} + 1$

$v$ に印をつける

if 白い辺 $v \rightarrow w$ がある then

if $w$ に印が付いていない then

$w \rightarrow v$ を緑色に塗る

$v \rightarrow w$ を赤色に塗る

$\texttt{RecTarry2}$($w, \mathit{clock}$)

else if 緑色の辺 $v \rightarrow w$ がある then

$\mathit{v.post} \leftarrow \mathit{clock};\ \mathit{clock} \leftarrow \mathit{clock} + 1$

$\texttt{RecTarry2}$($w, \mathit{clock}$)
あなたは $n$ 個の鍵のかかった箱と $m$ 個の黄金の鍵を持っています。それぞれの鍵が開けられるのは多くとも一つですが、箱の中には一つの鍵で開けられるものも、複数の鍵で開けられるものも、どの鍵でも開かないものもあります。鍵のかかった箱を開ける方法は二つしかありません: 正しい鍵を使って鍵を開けるか、ハンマーを使って叩き壊すかです。

光るもので遊ぶのが大好きな赤ん坊 (あなたの兄弟) が鍵を全て箱の中に入れてしまいました！あなたは全ての黄金の鍵をどうにかして取り出さなくてはなりません。幸いにもホームセキュリティシステムが全てを記録していたので、どの鍵がどの箱に入っているかは分かります。明らかなこととして、少なくとも一つの箱を叩き壊す必要があります。
1. あなたの赤ん坊の兄弟がハンマーを見つけて熱心に一つの箱を見つめています。あなたの兄弟が選んだ箱だけを叩き壊して全ての鍵を入手できるかどうかを判定するアルゴリズムを説明、解析してください。
2. 全ての鍵を回収するために叩き壊さなければならない箱の数の最小値を求めるアルゴリズムを説明、解析してください。
アルゴリズムの講義を担当しているあなたは、与えられたグラフのある頂点を根とした幅優先探索木と深さ優先探索木を書きなさいという問題を二回目の中間試験で出題しました。しかし試験の採点を始めたところ、問題に出したグラフには全域木が何種類も ――列挙しきれないほど―― 存在することが分かりました。どうにかして生徒の回答があっているかどうかを判定しなくてはなりません！

次の問題では、接続グラフ $G$ と開始頂点 $s$、そして $G$ の全域木 $T$ が与えられるとします。
1. $G$ が無向グラフだとします。$T$ が $s$ を根とする深さ優先全域木であるかを判定するアルゴリズムを説明、解析してください。
2. $G$ が無向グラフだとします。$T$ が $s$ を根とする幅優先全域木であるかを判定するアルゴリズムを説明、解析してください。 [ヒント: $T$ が重み無し最短路木であることを示すだけでは不十分です。えぇ、この問題は相応しいのはこの章です！]
3. $G$ が有向グラフだとします。$T$ が $s$ を根とする幅優先全域木であるかを判定するアルゴリズムを説明、解析してください。 [ヒント: (b) を先に解いてください]
4. $G$ が有向グラフだとします。$T$ が $s$ を根とする深さ優先全域木であるかを判定するアルゴリズムを説明、解析してください。
JavaScript, Python, Perl, Ruby といった現代的なプログラミング言語には並列代入 (parallel assignment) という機能があります。並列代入を使うと複数の代入を一行で書くことができ、例えば $\color{maroon}{\texttt{x, y = 0, 1}}$ という Python コードは $\color{maroon}{\texttt{x}}$ に $0$ を、$\color{maroon}{\texttt{y}}$ に $1$ を同時に代入します。この代入において右辺の値は変数の古い値を使って計算されます。そのため $\color{maroon}{\texttt{a, b = b, a}}$ という Python コードは $\color{maroon}{\texttt{a}}$ と $\color{maroon}{\texttt{b}}$ の値を交換し、次の Python コードは $n$ 番目の Fibonacci 数を計算します: \[ \begin{aligned} \color{maroon}{\begin{array}{l} \texttt{def fib(n):} \\ \quad \texttt{prev, curr = 1, 0} \\ \quad \texttt{while n > 0:} \\ \quad \quad \texttt{prev, curr, n = curr, prev+curr, n-1} \\ \quad \texttt{return curr} \end{array}} \end{aligned} \]

あなたは言語のインタープリタを書いていて、全ての並列代入を単純な代入の列に変換する必要があるとします。例えば、並列代入 $\color{maroon}{\texttt{a, b = 0, 1}}$ は $\color{maroon}{\texttt{a=0; b=1}}$ または $\color{maroon}{\texttt{b=1; a=0}}$ という二つの方法で単純な代入に変換できます。しかし $\color{maroon}{\texttt{x, y = x + 1, x + y}}$ という並列代入は $\color{maroon}{\texttt{y=x+y; x=x+1}}$ という順番にしか変換できません。さらに、一つ以上の一時的な変数が必要になることもあります。例えば $\color{maroon}{\texttt{a, b = b, a}}$ の変換には一つの一時的な変数が必要になり、$\color{maroon}{\texttt{x, y = x+y, x-y}}$ の変換には二つの一時的な変数が必要になります。
1. 与えられた並列代入が一時的な変数を使わずに単純な代入の列に変換できるかどうかを判定するアルゴリズムを説明してください。
2. 与えられた並列代入が一時的な変数をちょうど一つだけ使って単純な代入の列に変換できるかどうかを判定するアルゴリズムを説明してください。
並列代入には整数の変数だけが使われ、ポインタや配列を使った間接参照は無いとしてください。また左辺に二回以上現れる変数は存在せず、右辺の式には副作用が無いとしてください。代入の文をパースする処理の詳細については気にしないで、代入が適切なグラフで表現されているとしてください (適切なグラフがどのようなものかは説明すること)。

${}$

動的計画法
有向非巡回グラフ $G$ が与えられ、頂点がジョブを表し、辺がジョブの優先順位に関する制約を表すとします。つまり、各辺 $u \rightarrow v$ がジョブ $v$ が始まる前にジョブ $u$ が終わらなければならないことを示します。また各頂点 $v$ には対応するジョブの実行時間を表す重さ $T(v)$ が付いています。
1. $G$ に含まれるジョブを全て終わらせる最小の時間を計算するアルゴリズムを説明してください。
2. 最初のジョブを時間 $0$ に始めるとします。各頂点 $v$ について、ジョブ $v$ を開始できる最も早い時間を計算するアルゴリズムを説明してください。
3. 各頂点 $v$ について、優先順位に関する制約を破ることも、((a) で計算される) ジョブ全体の終了時間を増やすこともせずに $v$ を開始できる最も遅い時間を計算するアルゴリズムを説明してください。ただし $v$ 以外のジョブは ((b) で計算される) 最速の開始時間に開始されるとします。
$G$ を有向非巡回グラフとし、$G$ が唯一のソース $s$ と唯一のシンク $t$ を持つとします。
1. $G$ のハミルトン路 (Hamiltonian path) とは $G$ の全ての頂点を通る有向路のことを言います。$G$ にハミルトン路が存在するかどうかを判定するアルゴリズムを説明してください。
2. $G$ の頂点に重みが付いているとします。$s$ から $t$ に向かう路で最大の重みを持つものを見つける効率の良いアルゴリズムを説明してください。
3. $G$ の他に整数 $l$ が与えられるとします。$s$ から $t$ に向かう長さが $l$ 以下の路で最大の重みを持つものを見つける効率の良いアルゴリズムを説明してください (そのような路が一つ以上存在すると仮定してください)。
4. $G$ の頂点のいくつかに重要であることを示す印が付いているとし、追加の入力 $k$ が与えられるとします。$s$ から $t$ に向かう、長さが $l$ 以下の、 $k$ 個以上の重要な点を通る路で最大の重みを持つものを見つける効率の良いアルゴリズムを説明してください (そのような路が一つ以上存在すると仮定してください)。
5. $G$ における $s$ から $t$ への路の数を計算するアルゴリズムを説明してください (任意に大きい整数の足し算を $O(1)$ で行えるとしてください)。
$G$ を有向非巡回グラフとし、固定されたアルファベットで頂点がラベル付けされているとします。$A[1..l]$ を同じアルファベットの文字列とします。$G$ の任意の路に対して、通る頂点のラベルを繋げて得られる文字列を路のラベルとして定義します。
1. ラベルが $A$ である $G$ の路を見つけるか、そのような路が無ければそうだと正しく報告するアルゴリズムを説明してください。
2. ラベルが $A$ である $G$ の路の数を計算するアルゴリズムを説明してください (任意に大きい整数の足し算を $O(1)$ で行えるとしてください)。
3. ラベルが $A$ の部分列である $G$ の路で最長なものを見つけるアルゴリズムを説明してください。
4. ラベルが $A$ の超配列である $G$ の路で最短なものを見つけるアルゴリズムを説明してください。
5. ラベルと $A$ との編集距離が最小となる $G$ の路を見つけるアルゴリズムを説明してください。
多角路 (polygonal path) とは線分の列であって隣り合う線分が同じ点でくっついているものを言います。多角路に含まれる線分の端点を多角路の頂点と言います。多角路の長さは含まれる線分の長さの和を言います。頂点 $(x_{1}, y_{1})$, $(x_{2}, y_{2})$, $\ldots$, $(x_{k}, y_{k})$ で表される多角路が単調増加であるとは、全ての添え字 $i$ について $x_{i} < x_{i+1}$ かつ $y_{i} < y_{i+1}$ が成り立つことを言います。形式ばらずに言うと、全ての頂点が一つ前の頂点よりも右上方向に続いているならばその多角路は単調増加です。

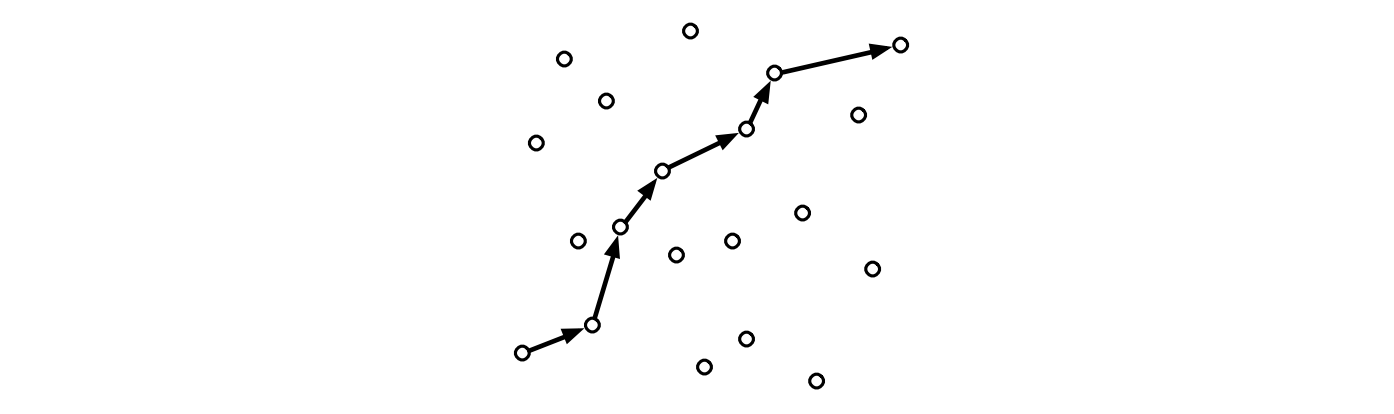図 6.22

点集合の中を通る 7 頂点の単調増加な多角路

$n$ 個の平面上の点の集合 $S$ が二つの配列 $X[1..n]$ と $Y[1..n]$ という形で与えられたとします。$S$ に含まれる最長の単調増加多角路を計算するアルゴリズムを説明、解析してください。二点 $x, y$ と $x^{\prime}, y^{\prime}$ の間の長さを計算するサブルーチン $\textsc{Length}(x, y, x^{\prime}, y^{\prime})$ が利用できるとしてください。
有向非巡回グラフ $G$ と任意の二つの頂点 $u, v$ について、$u$ から $v$ への全ての有向路の和集合を区間 $G[u,v]$ と言います。同じことを言い換えると、$G[u,v]$ は $x \in \mathit{reach}(u)$ かつ $v \in \mathit{reach}(x)$ を満たす頂点 $x$ とそれらの頂点を結ぶ $G$ の辺からなります。

辺に実数の重みが付いた有向非巡回グラフ $G$ が与えられたとします。
1. $G$ に含まれる区間で最大の重さを持つものを見つける効率の良いアルゴリズムを説明、解析してください。区間の重さとは含まれる頂点の重みの和です。辺の重みは負でもあり得ます。
2. $G$ に含まれる全ての区間に対して、その区間に含まれる一番重い頂点を計算する効率の良いアルゴリズムを説明してください。アルゴリズムが計算するのは二次元配列 $\mathit{MaxWt}[1..V, 1..V]$ であり、区間 $G[u,w]$ に含まれる中で一番重い頂点が $\mathit{MaxWt}[u,w]$ に含まれます。また $G[u,w]$ が空のときには $\mathit{MaxWt}[u,w] = -\infty$ であるべきです。
適当なアルファベットを固定し、頂点がそのアルファベットでラベル付けされた有向非巡回グラフを $G$ とします。$G$ の任意の路のラベルを、通る頂点のラベルを繋げて得られる文字列として定義します。また回文 (palindrome) とは逆に呼んでも同じになる文字列のことです。
1. $G$ の路が持つ回文のラベルで一番長いものの長さを計算するアルゴリズムを説明、解析してください。例えば次の図で表されるグラフに対するアルゴリズムの答えは $\color{maroon}{\texttt{HANNAH}}$ に対応する整数 $6$ です。
  
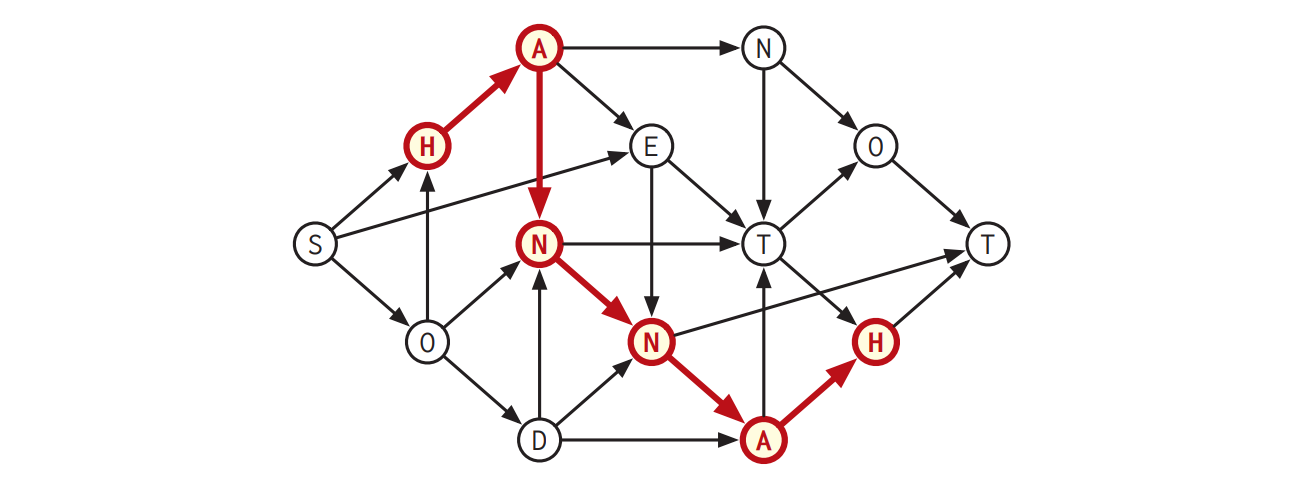  図 6.23
  
  ラベルが回文である最長の路の長さが 6 である DAG
2. $G$ に含まれる路のラベルの部分列である回文で最長のものを見つけるアルゴリズムを説明してください。
3. $G$ が単一のソース $s$ と単一のシンク $t$ を持つとします。$s$ から $t$ への路のラベルの超配列である回文で最長のものを見つけるアルゴリズムを説明してください。
二つの有向非巡回グラフ $G, H$ が与えられ、どちらの頂点も有限アルファベットでラベル付けされているとします (異なる頂点が同じラベルを持つことがあり得ます)。二つの DAG に含まれる任意の路のラベルを、通る頂点のラベルを繋げて得られる文字列として定義します。
1. $G$ の路のラベルであり $H$ の路のラベルでもあるような文字列のうち最長なものの長さを計算するアルゴリズムを説明、解析してください。
2. $G$ の路のラベルの部分列であり $H$ の路のラベルの部分列でもあるような文字列のうち最長なものの長さを計算するアルゴリズムを説明、解析してください。
3. $G$ の路のラベルの超配列であり $H$ の路のラベルの超配列でもあるような文字列のうち最短なものの長さを計算するアルゴリズムを説明、解析してください。 [ヒント: 見た目よりも簡単です。]
$G$ を任意の有向グラフとします (非巡回とは限りません)。$G$ の各頂点 $v$ は重み $w(v)$ を持つとします。
1. 含まれる頂点の重みの列が増加列である $G$ の有向路で最長なものを見つけるアルゴリズムを説明してください。
2. $G$ の全ての頂点に対して、その頂点から到達できる頂点の重みの最大値を計算するアルゴリズムを説明、解析してください。つまり、アルゴリズムは全ての頂点 $v$ に対して $\mathit{maxreach}(v) :=$ $\max \lbrace w(x)\ |\ x \in \mathit{reach}(v) \rbrace$ を計算します。
1. $n$ 個の頂点を持つ有向非巡回グラフ $G$ と整数 $k \leq n$ が与えられたとします。全ての頂点を覆う互いに頂点が重ならない最大 $k$ 個の路の集合を計算する効率の良いアルゴリズムを説明してください。
2. $n$ 個の頂点を持つ有向非巡回グラフ $G$ と整数 $k \leq n$ が与えられ、辺に (負でもあり得る) 重みが付いているとします。全ての頂点を覆う互いに頂点が重ならない最大 $k$ 個の路の集合であって重みの和が最小なものを計算する効率の良いアルゴリズムを説明してください。
答えのアルゴリズムの実行時間は小さな定数 $c$ に対して $O(n^{k+c})$ である必要があります。また一つの頂点の路としての重みは $0$ です (十一章で (a) に対するより効率的なアルゴリズムを見ます)。
プロのロッククライマー Kris は全米選手権に出場します。選手権ではクライミングウォールにあるホールドを使うときに許されている動きが審判によって設定され、そのルールの下で一番多くホールドを使った選手の勝ちです。

クライミングウォールには $n$ 個のホールドがあり、Kris には $(x, y)$ の形をした組が $m$ 個与えられ、各組が $y$ 番目のホールドから $x$ 番目のホールドへの移動が許されていることを表します。Kris は点数を最大化するために、なるべく長い許された移動の列を見つける必要があります。Kris は最初と最後のホールドを選ぶことができます。また同じホールドは何度でも使うことができますが、点数が増えるのは最初に訪れたときだけです。
1. 入力を表す自然なグラフを定義します。このグラフが DAG であることが保証されているときに、Kris のクライミング問題を解くアルゴリズムを説明、解析してください。
2. 入力グラフに制約が無い場合に Kris のクライミング問題を解くアルゴリズムを説明、解析してください。
両方のアルゴリズムの出力は Kris の獲得できる最大得点としてください。
$n$ 個の銀河を結ぶ $m$ 個の銀河間テレポートウェイがあります。各テレポートウェイは二つの銀河を結んでいて、双方向に使うことができます。テレポートウェイを管理している会社は自分たちにとても有利な料金体系を敷いています: 自分の銀河から遠ざかる方向に向かうテレポートは無料なのですが、自分の銀河に近づく方向のテレポートはとても高額です。

Judy は大学のサバティカルを使った旅行でできる限り多くの銀河を訪れることにしました。旅行は彼女の銀河から始まります。旅行代を浮かせるために、最後の一回を除いた全てのテレポートは自分の銀河から遠ざかる方向にしたいと彼女は考えています。
1. Judy が訪れることができる銀河の数の最大値を計算するアルゴリズムを説明、解析してください。アルゴリズムの入力はテレポートウェイのネットワークを表す $n$ 個の頂点と $m$ 個の辺を持つ無向グラフ $G$ と Judy の住む銀河を表す整数 $1 \leq s \leq n$、そして銀河 $s$ から各銀河への距離を表す配列 $D[1..n]$ です。
2. ❤ 銀河をめぐる旅行に出かけようとしたちょうどそのとき、Judy は宇宙宝くじに当選し、自分の銀河に向かうテレポート一回分の金額を手に入れました。これで Judy は自分の銀河に向かうテレポートを二回行えることになります。Judy が訪れることができる銀河の数の最大値を計算するアルゴリズムを説明、解析してください。同じ銀河を二回訪れても構いませんが、訪れた銀河の数に数えるのは最初の一回だけです。
ドクターと River Song は有向非巡回グラフ $G$ を使ったゲームをすることになりました。$G$ には一つのソース $s$ と一つのシンク $t$ が含まれます⁷。

二人のプレイヤーは $G$ の頂点に駒を置きます。ゲームの開始時ドクターの駒はソース頂点 $s$ に、River の駒はシンク頂点 $t$ にあり、プレイヤーはドクターから始めて交互に駒を動かします。各ターンでドクターは有向辺に沿って駒を進め、River は有向辺の逆方向に駒を勧めます。

二つの駒が一つの頂点で出会ったら River の勝ち ("Hello, Sweetie!") で、River の駒が $s$ に着くかドクターの駒が $t$ に着いたらドクターの勝ちです。

二人のプレイヤーが完璧にプレイしたときに誰がゲームに勝つかを判定するアルゴリズムを説明、解析してください。つまり、River がどんな動きをしたとしてもドクターが勝つことができるならアルゴリズムの出力は "Doctor" であり、ドクターがどんな動きをしたとしても River が勝つことができるならアルゴリズムの出力は "River" です (なぜこの二つの可能性しかないのでしょうか？)。アルゴリズムの入力はグラフ $G$ です。
♣ ❤ $x = x_{1} x_{2} \ldots x_{n}$ を適当な有限アルファベット上の $n$ 文字の文字列とし、$A$ を同じアルファベットに対する $m$ 状態の決定性有限状態機械とします。
1. $A$ によって受理される $x$ の部分列で最長のものの長さを求めるアルゴリズムを説明、解析してください。例えば、$A$ が言語 $\texttt{({\color{maroon}AR})}^{\ast}$ を受理する機械で $x = \texttt{\color{maroon}{\underline{A}B\underline{R}AC\underline{A}DAV\underline{R}A}}$ である場合、アルゴリズムの出力は文字列 $\texttt{\color{maroon}{ARAR}}$ に対応する $4$ です。
2. $A$ によって受理される $x$ の超配列で最短のものの長さを求めるアルゴリズムを説明、解析してください。例えば、$A$ が言語 $\texttt{({\color{maroon}ABCDR})}^{\ast}$ を受理する機械で $x = \texttt{\color{maroon}{ABRACADABRA}}$ である場合、アルゴリズムの出力は文字列 $\texttt{\color{maroon}\underline{AB}CD}$$\texttt{\color{maroon}\underline{RA}B\underline{C}}$$\texttt{\color{maroon}DR\underline{A}BC}$$\texttt{\color{maroon}\underline{D}R\underline{AB}}$$\texttt{\color{maroon}CD\underline{RA}}$$\texttt{\color{maroon}BCDR}$ に対応する $25$ です。
アルゴリズムの解析は入力文字列の長さ $n$ と有限状態機械の状態数 $m$ とアルファベット $\Sigma$ のサイズを使って行ってください。
全ての動的計画法の問題が有向非巡回グラフにおける最適路を見つける問題として表せるわけではありません。しかし全ての動的計画法のアルゴリズムはその問題に応じたなんらかの依存グラフを帰りがけ順で処理します。
1. 有向非巡回グラフ $G$ が与えられ、各頂点に探索の時に鍵となる数値が保存されているとします。二分探索木となっている $G$ の部分グラフで最大のものを見つけるアルゴリズムを説明、解析してください。
2. 有向非巡回グラフ $G$ と二つの頂点 $s, t$ が与えられたとします。$s$ から $t$ への路の数を計算するアルゴリズムを説明してください (算術計算は $O(1)$ 時間でできるとしてください)。
3. $G$ を次の条件を満たす有向非巡回グラフとします:
  - $G$ には一つのソース $s$ といくつかのシンク $t_{1}, t_{2}, \cdots, t_{k}$ がある。
  - 各辺 $v \rightarrow w$ には $0$ か $1$ の重み $p(v \rightarrow w)$ がある。
  - シンクでない全ての頂点 $v$ について、$v$ を始点とする辺の重みの和は $1$ である。つまり、$\sum_{v} p(v \rightarrow w) = 1$ が成り立つ。
  重み $p(v \rightarrow w)$ は $G$ における $s$ から $t$ へのランダムウォークを定義します: シンクでない頂点 $v$ についたとき、歩行者は確率 $p(v \rightarrow w)$ で $v \rightarrow w$ をたどります (全ての確率は互いに独立です)。全ての添え字 $i$ について、このランダムウォークが $t_{i}$ にたどり着く確率を計算するアルゴリズムを説明、解析してください (算術計算は $O(1)$ 時間でできるとしてください)。

これら二つのラッパー関数が同じになるのは深さ優先探索においてだけです。特に幅優先探索の場合、for ループで包んで全ての頂点を訪れるようにした探索と新しく追加したソース頂点から始める探索では頂点を訪れる順番が全く異なります。^[return]
紛らわしいことに、この二つの順序は両方とも「深さ優先順序 (depth-ordering)」と呼ばれることがあります。あなたはこういうことをしないでください。^[return]
$G$ の逆の帰りがけ順序が $G$ の帰りがけ順序の逆順であるとは限りませんが、$G$ のトポロジカル順序であることは言えます。^[return]
もう一度書いておきます: $\mathit{rev}(G)$ の帰りがけ順の逆順は $G$ の帰りがけ順と等しくはありません。^[return]
同じアルゴリズムが Kosaraju よりも前にロシアの文献に登場するという噂がありますが、この噂を裏付ける信頼できるソースを見つけることができませんでした。^[return]
伝説によると、Kosaraju はアルゴリズムの講義中にこのアルゴリズム発見したと言われています。彼は Tarjan のアルゴリズムを説明することになっていたのですが、ノートを忘れてしまったのでその場で埋め合わせをしなければならなかったそうです。この話について私が唯一驚くのは、誰も Sharir と Tarjan については同じことを言わない点です。^[return]
$s$ と $t$ というラベルは the Untempered Schism と the Time Vortex、あるいは the Shining World of the Seven Systems (Gallifrey としても知られる) と Trenzalore、あるいは Skaro と Telos、あるいは "Something else Timey-wimey" の頭文字をとったものです。とにかくすごく複雑なので、気にしないでください。^[return]