練習問題

深さ優先探索・トポロジカルソート・強連結成分

1. 有向グラフ $G$ の逆 $\mathit{rev}(G)$ を $O(V+E)$ 時間で計算するアルゴリズムを説明してください。
2. 任意の有向グラフ $G$ について、強連結成分グラフ $\mathit{scc}(G)$ が非巡回であることを示してください。
3. 任意の有向グラフ $G$ について、$\mathit{scc}(\mathit{rev}(G)) = \mathit{rev}(\mathit{scc}(G))$ を示してください。
4. 有向グラフ $G$ を固定します。$G$ の任意の頂点 $v$ について、$S(v)$ で $v$ を含む $G$ の強連結成分を表すことにします。$G$ の任意の頂点 $u, v$ について、$G$ において $v$ が $u$ に到達可能なことと $\mathit{scc}(G)$ において $S(v)$ が $S(u)$ に到達可能なことが同値だと示してください。
5. 有向グラフ $G$ の二つの強連結成分を $S, T$ とします。任意の $u \in S$ と $v \in T$ に対して $\mathit{finish}(u) < \mathit{finish}(v)$ であるか、そうでなければ任意の $u \in S$ と $v \in T$ に対して $\mathit{finish}(u) > \mathit{finish}(v)$ であることを示してください。
有向グラフ $G$ が半接続 (semi-connected) であるとは、任意の頂点の組 $u, v$ について、$u$ が $v$ に到達可能であるか $v$ が $u$ に到達可能なことを言います (両方向に到達可能でも構いません)。
1. ソース頂点を一つだけ持つ DAG であって半接続でないものの例を一つ示してください。
2. 与えられた有向非巡回グラフが半接続かどうかを判定するアルゴリズムを説明、解析してください。
3. 制約のない任意の有向グラフが半接続かどうかを判定するアルゴリズムを説明、解析してください。
Sham-Poobanana 市警察署は市内全ての道路を一方通行にすることを決定しました。自動車を運転する人が困惑しきって大勢文句を言ったにもかかわらず、市長は Sham-Poobanana 市内の任意の交差点の間は合法的に行き来できると言って聞きません。
1. 市は市長の主張を検証または反証しなければなりません。この問題をグラフの問題として定式化し、その問題を解くアルゴリズムを説明、解析してください。
2. (a) のアルゴリズムを実行したところ、市長は ~~嘘をついていた~~ 情報が間違って伝わっていたことを渋々認めました。市長がこの暴露を受けて主張したことによると、 Sham-Poobanana 市内の交差点のうち 95 % 以上は良い交差点であるとのことです。交差点 $x$ が良いとは、$x$ から到達できる全ての交差点 $y$ について $y$ から $x$ に到達できることを言います。彼女の主張を検証または反証する効率の良いアルゴリズムを説明、解析してください。
満点のためには、両方のアルゴリズムが線形時間で実行できることが求められます。
有向非巡回グラフ $G$ が唯一のソース $s$ と唯一のシンク $t$ を持つとします。頂点 $v \notin \lbrace s, t \rbrace$ が $\pmb{(s, t)}$-切断点であるとは、$s$ から $t$ への任意の路が $v$ を通ることを言います。同じことを言い換えると、$v$ を削除すると $s$ から $v$ に到達できなくなるならば $v$ は $(s,t)$-切断点です。$G$ の $(s,t)$-切断点を全て見つけるアルゴリズムを説明してください。

$三つの $(s,t)$-切断頂点を持つ DAG$

図 6.20

三つの $(s,t)$-切断頂点を持つ DAG
連結無向グラフ $G$ の頂点 $v$ が切断点 (cut vertex) であるとは、部分グラフ $G - v$ ($G$ から $v$ を取り除いて得られるグラフ) が非連結であることを言います。

図 6.21

四つの切断点を持つ無向グラフ
1. グラフ $G$ と頂点 $v$ が与えられたときに、$v$ が切断点であるかを判定する線形時間アルゴリズムを説明してください。全ての頂点に対してそのアルゴリズムを試した場合、全ての切断点を見つけるのにどれだけ時間がかかりますか？
2. 無向グラフ $G$ の深さ優先全域木を $T$ とします。
  1. $T$ の根が $G$ の切断点であるのはその根が $T$ で二つ以上の子を持つときに限ることを示してください。
  2. 根でない頂点 $v$ が $G$ の切断点であるのは、$v$ の ($T$ における) 子の ($T$ における) 子孫が $v$ の ($T$ における) 真の先祖に ($G$ で) 隣接するときに限ることを示してください。
  [ヒント: $T$ が深さ優先探索探索木でなかったり、$G$ が有向グラフであったりするとこれらの命題は成り立たなくなります。]
3. 無向グラフに含まれる全ての切断点を $O(V + E)$ 時間で見つけるアルゴリズムを説明してください。
連結無向グラフ $G$ の辺 $e$ が切断辺であるとは、部分グラフ $G - e$ ($G$ から $e$ を取り除いて得られるグラフ) が非連結であることを言います。
1. グラフ $G$ と頂点 $e$ が与えられたときに、$e$ が切断辺であるかを判定する線形時間アルゴリズムを説明してください。全ての辺に対してそのアルゴリズムを試した場合、全ての切断辺を見つけるのにどれだけ時間がかかりますか？
2. $G$ の任意の全域木を $T$ とします。$G$ の切断辺が $T$ の切断辺でもあることを示してください。この命題から、$G$ の切断辺は最大でも $V-1$ 本であることが分かります。(a) で答えた全ての切断辺を見つけるアルゴリズムはこの情報によってどの程度改善されますか？
3. $T$ の根を適当な頂点 $r$ に固定したとします。各頂点 $v$ について、$T_{v}$ で $v$ を根とする $T$ の部分木を表すことにします。例えば $T_{r} = T$ です。$uv$ を $T$ の任意の辺とし、$u$ が $v$ の親であるとします。$uv$ が $G$ の切断辺であるのは $G$ の辺で端点のちょうど片方が $T_{v}$ に属する唯一の辺が $uv$ である場合に限ることを示してください。
4. $G$ に含まれる全ての切断辺を見つける線形時間アルゴリズムを説明してください。 [ヒント: $G$ の深さ優先探索木を $T$ とします。]
有向グラフ $G$ の推移閉包 (transitive closure) $G^{T}$ とは $G$ と同じ頂点を持つグラフであって、辺 $u \rightarrow v$ が存在するのが $G$ に $u$ から $v$ への有向路が存在するときに限るものです。$G$ の推移縮約 (transitive reduction) とは推移閉包が $G^{T}$ と等しくなる最小の辺の集合です。グラフに対する推移縮約は一つだけとは限りません。
1. 与えられた有向グラフの推移閉包を効率良く計算するアルゴリズムを説明してください。
2. 有向グラフ $G$ の推移縮約が唯一であるのは $G$ が非巡回な場合に限ることを示してください。
3. 与えられた有向グラフの推移縮約を効率良く計算するアルゴリズムを説明してください。
任意の接続グラフに適用できる最も古いアルゴリズムの一つは、1895 年に Gaston Tarry (ガストン・タリー) によって迷路を解くために提案されました。Tarry のアルゴリズムに対する入力は無向グラフ $G$ ですが、表現を簡単にするために辺 $uv$ を二つの有向辺 $u \rightarrow v$ と $v \rightarrow u$ に分割します。(実際のプログラムにはこの分割に対応する処理は存在しません。アルゴリズムは与えられた $G$ の隣接リストが有向であると思って処理を行うだけです)。

くだけて説明すると、Tarry のアルゴリズムは頂点 $v$ を "訪れる" たびに $v$ に印を付け、$v \rightarrow w$ を赤く塗って $\textsc{RecTarry}(w)$ を呼ぶことで "走査" を行います。これまでに見たグラフの走査アルゴリズムと違って、Tarry のアルゴリズムは同じ頂点に複数回印を付けることがあります。

procedure $\texttt{Tarry}$($G$)

$G$ の全ての頂点の印を消す

$G$ の全ての辺を白く塗る

$s \leftarrow G$ の適当な頂点

$\texttt{RecTarry}$($s$)

procedure $\texttt{RecTarry}$($v$)

⟨⟨$v$ を訪れる⟩⟩

$v$ に印をつける $\quad$

if 白い辺 $v \rightarrow w$ がある then

if $w$ に印が付いていない then

$w \rightarrow v$ を緑色に塗る

⟨⟨$v \rightarrow w$ を走査する⟩⟩

$v \rightarrow w$ を赤色に塗る

$\texttt{RecTarry}$($w$)

else if 緑色の辺 $v \rightarrow w$ がある then

⟨⟨$v \rightarrow w$ を走査する⟩⟩

$v \rightarrow w$ を赤色に塗る

$\texttt{RecTarry}$($w$)
1. $O(V+E)$ 時間で動作する Tarry のアルゴリズムの実装を説明してください。
2. 二回以上走査される $G$ の有向辺が存在しないことを示してください。
3. このアルゴリズムが頂点 $v$ を $k$ 回目に訪れたとき、$v$ に向かう赤い辺と $v$ から出る赤い辺はそれぞれ何本ですか？ [ヒント: 開始頂点 $s$ とそれ以外の頂点を分けて考えてください。]
4. このアルゴリズムが開始頂点 $s$ 以外の頂点 $v$ を最大でも $\deg (v)$ 回訪れることを示してください。なお開始頂点では最大 $\deg(s) + 1$ 回となります。このことから $\textsc{Tarry}(G)$ が停止することが直ちに分かります。
5. $\textsc{Tarry}(G)$ が最後に訪れる頂点は開始頂点 $s$ であることを示してください。
6. $\textsc{Tarry}(G)$ が終了したとき、 $\textsc{Tarry}(G)$ が訪れる全ての頂点 $v$ について、 $v$ に向かう辺と $v$ から出る辺が全て赤いことを示してください。 [ヒント: 開始頂点 $s$ から始まる最初に頂点に印が付く順番を考え、帰納法を使います。]
7. $\textsc{Tarry}(G)$ が $G$ の全ての頂点を訪れることを示してください。これと前問の主張を組み合わせると、$\textsc{Tarry}(G)$ が $G$ の全ての辺をちょうど一回ずつ走査することが分かります。
Tarry のグラフ走査アルゴリズムの次の変種を考えます。ここでは緑色の辺を走査してもその辺を赤く塗り直すことはせず、その代わり各頂点に二つの数値を割り振ります:

次の主張を証明または反証してください: 「$\textsc{Tarry2}(G)$ が停止したとき、緑色の辺は全域木を定義し、 $\mathit{v.pre}$ と $\mathit{v.post}$ のラベルはそれぞれ行きがけ順および帰りがけ順のラベルであり、全て $G$ のある深さ優先探索で得られるものと等しい」言い換えると、$\textsc{Tarry2}(G)$ が辺を訪れる順番は深さ優先探索と全く違うにもかかわらず、出力が深さ優先探索と同じであることを証明または反証してください。

procedure $\texttt{Tarry2}$($G$)

$G$ の全ての頂点の印を消す

$G$ の全ての辺を白く塗る

$s \leftarrow G$ の適当な頂点

$\texttt{RecTarry2}$($s, 1$)

procedure $\texttt{RecTarry2}$($v, \mathit{clock}$)

if $v$ に印が付いていない then

$\mathit{v.pre} \leftarrow \mathit{clock};\ \mathit{clock} \leftarrow \mathit{clock} + 1$

$v$ に印をつける

if 白い辺 $v \rightarrow w$ がある then

if $w$ に印が付いていない then

$w \rightarrow v$ を緑色に塗る

$v \rightarrow w$ を赤色に塗る

$\texttt{RecTarry2}$($w, \mathit{clock}$)

else if 緑色の辺 $v \rightarrow w$ がある then

$\mathit{v.post} \leftarrow \mathit{clock};\ \mathit{clock} \leftarrow \mathit{clock} + 1$

$\texttt{RecTarry2}$($w, \mathit{clock}$)
あなたは $n$ 個の鍵のかかった箱と $m$ 個の黄金の鍵を持っています。それぞれの鍵が開けられるのは多くとも一つですが、箱の中には一つの鍵で開けられるものも、複数の鍵で開けられるものも、どの鍵でも開かないものもあります。鍵のかかった箱を開ける方法は二つしかありません: 正しい鍵を使って鍵を開けるか、ハンマーを使って叩き壊すかです。

光るもので遊ぶのが大好きな赤ん坊 (あなたの兄弟) が鍵を全て箱の中に入れてしまいました！あなたは全ての黄金の鍵をどうにかして取り出さなくてはなりません。幸いにもホームセキュリティシステムが全てを記録していたので、どの鍵がどの箱に入っているかは分かります。明らかなこととして、少なくとも一つの箱を叩き壊す必要があります。
1. あなたの赤ん坊の兄弟がハンマーを見つけて熱心に一つの箱を見つめています。あなたの兄弟が選んだ箱だけを叩き壊して全ての鍵を入手できるかどうかを判定するアルゴリズムを説明、解析してください。
2. 全ての鍵を回収するために叩き壊さなければならない箱の数の最小値を求めるアルゴリズムを説明、解析してください。
アルゴリズムの講義を担当しているあなたは、与えられたグラフのある頂点を根とした幅優先探索木と深さ優先探索木を書きなさいという問題を二回目の中間試験で出題しました。しかし試験の採点を始めたところ、問題に出したグラフには全域木が何種類も ――列挙しきれないほど―― 存在することが分かりました。どうにかして生徒の回答があっているかどうかを判定しなくてはなりません！

次の問題では、接続グラフ $G$ と開始頂点 $s$、そして $G$ の全域木 $T$ が与えられるとします。
1. $G$ が無向グラフだとします。$T$ が $s$ を根とする深さ優先全域木であるかを判定するアルゴリズムを説明、解析してください。
2. $G$ が無向グラフだとします。$T$ が $s$ を根とする幅優先全域木であるかを判定するアルゴリズムを説明、解析してください。 [ヒント: $T$ が重み無し最短路木であることを示すだけでは不十分です。えぇ、この問題は相応しいのはこの章です！]
3. $G$ が有向グラフだとします。$T$ が $s$ を根とする幅優先全域木であるかを判定するアルゴリズムを説明、解析してください。 [ヒント: (b) を先に解いてください]
4. $G$ が有向グラフだとします。$T$ が $s$ を根とする深さ優先全域木であるかを判定するアルゴリズムを説明、解析してください。
JavaScript, Python, Perl, Ruby といった現代的なプログラミング言語には並列代入 (parallel assignment) という機能があります。並列代入を使うと複数の代入を一行で書くことができ、例えば $\color{maroon}{\texttt{x, y = 0, 1}}$ という Python コードは $\color{maroon}{\texttt{x}}$ に $0$ を、$\color{maroon}{\texttt{y}}$ に $1$ を同時に代入します。この代入において右辺の値は変数の古い値を使って計算されます。そのため $\color{maroon}{\texttt{a, b = b, a}}$ という Python コードは $\color{maroon}{\texttt{a}}$ と $\color{maroon}{\texttt{b}}$ の値を交換し、次の Python コードは $n$ 番目の Fibonacci 数を計算します: \[ \begin{aligned} \color{maroon}{\begin{array}{l} \texttt{def fib(n):} \\ \quad \texttt{prev, curr = 1, 0} \\ \quad \texttt{while n > 0:} \\ \quad \quad \texttt{prev, curr, n = curr, prev+curr, n-1} \\ \quad \texttt{return curr} \end{array}} \end{aligned} \]

あなたは言語のインタープリタを書いていて、全ての並列代入を単純な代入の列に変換する必要があるとします。例えば、並列代入 $\color{maroon}{\texttt{a, b = 0, 1}}$ は $\color{maroon}{\texttt{a=0; b=1}}$ または $\color{maroon}{\texttt{b=1; a=0}}$ という二つの方法で単純な代入に変換できます。しかし $\color{maroon}{\texttt{x, y = x + 1, x + y}}$ という並列代入は $\color{maroon}{\texttt{y=x+y; x=x+1}}$ という順番にしか変換できません。さらに、一つ以上の一時的な変数が必要になることもあります。例えば $\color{maroon}{\texttt{a, b = b, a}}$ の変換には一つの一時的な変数が必要になり、$\color{maroon}{\texttt{x, y = x+y, x-y}}$ の変換には二つの一時的な変数が必要になります。
1. 与えられた並列代入が一時的な変数を使わずに単純な代入の列に変換できるかどうかを判定するアルゴリズムを説明してください。
2. 与えられた並列代入が一時的な変数をちょうど一つだけ使って単純な代入の列に変換できるかどうかを判定するアルゴリズムを説明してください。
並列代入には整数の変数だけが使われ、ポインタや配列を使った間接参照は無いとしてください。また左辺に二回以上現れる変数は存在せず、右辺の式には副作用が無いとしてください。代入の文をパースする処理の詳細については気にしないで、代入が適切なグラフで表現されているとしてください (適切なグラフがどのようなものかは説明すること)。

${}$

動的計画法
有向非巡回グラフ $G$ が与えられ、頂点がジョブを表し、辺がジョブの優先順位に関する制約を表すとします。つまり、各辺 $u \rightarrow v$ がジョブ $v$ が始まる前にジョブ $u$ が終わらなければならないことを示します。また各頂点 $v$ には対応するジョブの実行時間を表す重さ $T(v)$ が付いています。
1. $G$ に含まれるジョブを全て終わらせる最小の時間を計算するアルゴリズムを説明してください。
2. 最初のジョブを時間 $0$ に始めるとします。各頂点 $v$ について、ジョブ $v$ を開始できる最も早い時間を計算するアルゴリズムを説明してください。
3. 各頂点 $v$ について、優先順位に関する制約を破ることも、((a) で計算される) ジョブ全体の終了時間を増やすこともせずに $v$ を開始できる最も遅い時間を計算するアルゴリズムを説明してください。ただし $v$ 以外のジョブは ((b) で計算される) 最速の開始時間に開始されるとします。
$G$ を有向非巡回グラフとし、$G$ が唯一のソース $s$ と唯一のシンク $t$ を持つとします。
1. $G$ のハミルトン路 (Hamiltonian path) とは $G$ の全ての頂点を通る有向路のことを言います。$G$ にハミルトン路が存在するかどうかを判定するアルゴリズムを説明してください。
2. $G$ の頂点に重みが付いているとします。$s$ から $t$ に向かう路で最大の重みを持つものを見つける効率の良いアルゴリズムを説明してください。
3. $G$ の他に整数 $l$ が与えられるとします。$s$ から $t$ に向かう長さが $l$ 以下の路で最大の重みを持つものを見つける効率の良いアルゴリズムを説明してください (そのような路が一つ以上存在すると仮定してください)。
4. $G$ の頂点のいくつかに重要であることを示す印が付いているとし、追加の入力 $k$ が与えられるとします。$s$ から $t$ に向かう、長さが $l$ 以下の、 $k$ 個以上の重要な点を通る路で最大の重みを持つものを見つける効率の良いアルゴリズムを説明してください (そのような路が一つ以上存在すると仮定してください)。
5. $G$ における $s$ から $t$ への路の数を計算するアルゴリズムを説明してください (任意に大きい整数の足し算を $O(1)$ で行えるとしてください)。
$G$ を有向非巡回グラフとし、固定されたアルファベットで頂点がラベル付けされているとします。$A[1..l]$ を同じアルファベットの文字列とします。$G$ の任意の路に対して、通る頂点のラベルを繋げて得られる文字列を路のラベルとして定義します。
1. ラベルが $A$ である $G$ の路を見つけるか、そのような路が無ければそうだと正しく報告するアルゴリズムを説明してください。
2. ラベルが $A$ である $G$ の路の数を計算するアルゴリズムを説明してください (任意に大きい整数の足し算を $O(1)$ で行えるとしてください)。
3. ラベルが $A$ の部分列である $G$ の路で最長なものを見つけるアルゴリズムを説明してください。
4. ラベルが $A$ の超配列である $G$ の路で最短なものを見つけるアルゴリズムを説明してください。
5. ラベルと $A$ との編集距離が最小となる $G$ の路を見つけるアルゴリズムを説明してください。
多角路 (polygonal path) とは線分の列であって隣り合う線分が同じ点でくっついているものを言います。多角路に含まれる線分の端点を多角路の頂点と言います。多角路の長さは含まれる線分の長さの和を言います。頂点 $(x_{1}, y_{1})$, $(x_{2}, y_{2})$, $\ldots$, $(x_{k}, y_{k})$ で表される多角路が単調増加であるとは、全ての添え字 $i$ について $x_{i} < x_{i+1}$ かつ $y_{i} < y_{i+1}$ が成り立つことを言います。形式ばらずに言うと、全ての頂点が一つ前の頂点よりも右上方向に続いているならばその多角路は単調増加です。

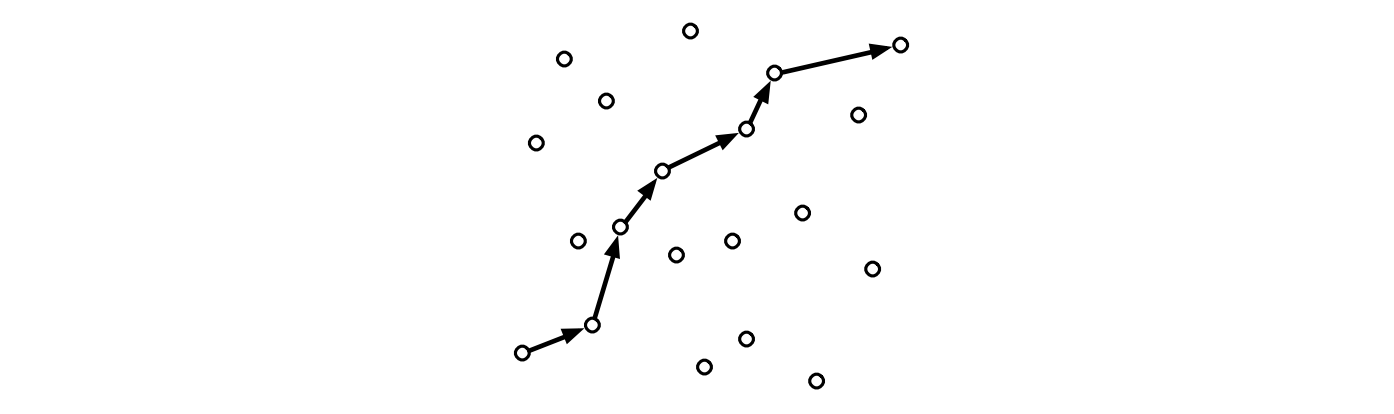図 6.22

点集合の中を通る 7 頂点の単調増加な多角路

$n$ 個の平面上の点の集合 $S$ が二つの配列 $X[1..n]$ と $Y[1..n]$ という形で与えられたとします。$S$ に含まれる最長の単調増加多角路を計算するアルゴリズムを説明、解析してください。二点 $x, y$ と $x^{\prime}, y^{\prime}$ の間の長さを計算するサブルーチン $\textsc{Length}(x, y, x^{\prime}, y^{\prime})$ が利用できるとしてください。
有向非巡回グラフ $G$ と任意の二つの頂点 $u, v$ について、$u$ から $v$ への全ての有向路の和集合を区間 $G[u,v]$ と言います。同じことを言い換えると、$G[u,v]$ は $x \in \mathit{reach}(u)$ かつ $v \in \mathit{reach}(x)$ を満たす頂点 $x$ とそれらの頂点を結ぶ $G$ の辺からなります。

辺に実数の重みが付いた有向非巡回グラフ $G$ が与えられたとします。
1. $G$ に含まれる区間で最大の重さを持つものを見つける効率の良いアルゴリズムを説明、解析してください。区間の重さとは含まれる頂点の重みの和です。辺の重みは負でもあり得ます。
2. $G$ に含まれる全ての区間に対して、その区間に含まれる一番重い頂点を計算する効率の良いアルゴリズムを説明してください。アルゴリズムが計算するのは二次元配列 $\mathit{MaxWt}[1..V, 1..V]$ であり、区間 $G[u,w]$ に含まれる中で一番重い頂点が $\mathit{MaxWt}[u,w]$ に含まれます。また $G[u,w]$ が空のときには $\mathit{MaxWt}[u,w] = -\infty$ であるべきです。
適当なアルファベットを固定し、頂点がそのアルファベットでラベル付けされた有向非巡回グラフを $G$ とします。$G$ の任意の路のラベルを、通る頂点のラベルを繋げて得られる文字列として定義します。また回文 (palindrome) とは逆に呼んでも同じになる文字列のことです。
1. $G$ の路が持つ回文のラベルで一番長いものの長さを計算するアルゴリズムを説明、解析してください。例えば次の図で表されるグラフに対するアルゴリズムの答えは $\color{maroon}{\texttt{HANNAH}}$ に対応する整数 $6$ です。
  
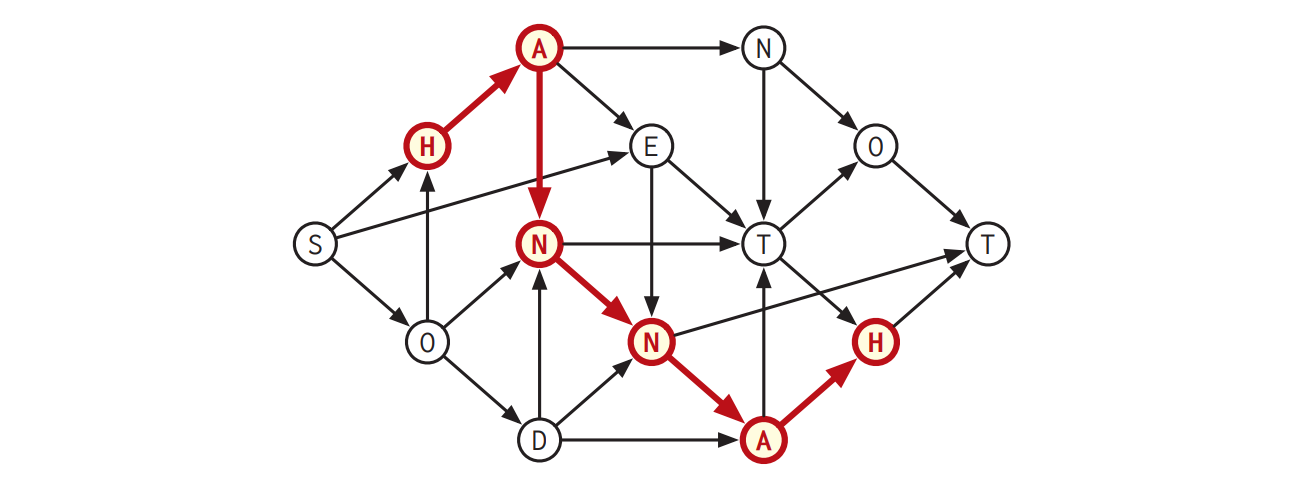  図 6.23
  
  ラベルが回文である最長の路の長さが 6 である DAG
2. $G$ に含まれる路のラベルの部分列である回文で最長のものを見つけるアルゴリズムを説明してください。
3. $G$ が単一のソース $s$ と単一のシンク $t$ を持つとします。$s$ から $t$ への路のラベルの超配列である回文で最長のものを見つけるアルゴリズムを説明してください。
二つの有向非巡回グラフ $G, H$ が与えられ、どちらの頂点も有限アルファベットでラベル付けされているとします (異なる頂点が同じラベルを持つことがあり得ます)。二つの DAG に含まれる任意の路のラベルを、通る頂点のラベルを繋げて得られる文字列として定義します。
1. $G$ の路のラベルであり $H$ の路のラベルでもあるような文字列のうち最長なものの長さを計算するアルゴリズムを説明、解析してください。
2. $G$ の路のラベルの部分列であり $H$ の路のラベルの部分列でもあるような文字列のうち最長なものの長さを計算するアルゴリズムを説明、解析してください。
3. $G$ の路のラベルの超配列であり $H$ の路のラベルの超配列でもあるような文字列のうち最短なものの長さを計算するアルゴリズムを説明、解析してください。 [ヒント: 見た目よりも簡単です。]
$G$ を任意の有向グラフとします (非巡回とは限りません)。$G$ の各頂点 $v$ は重み $w(v)$ を持つとします。
1. 含まれる頂点の重みの列が増加列である $G$ の有向路で最長なものを見つけるアルゴリズムを説明してください。
2. $G$ の全ての頂点に対して、その頂点から到達できる頂点の重みの最大値を計算するアルゴリズムを説明、解析してください。つまり、アルゴリズムは全ての頂点 $v$ に対して $\mathit{maxreach}(v) :=$ $\max \lbrace w(x)\ |\ x \in \mathit{reach}(v) \rbrace$ を計算します。
1. $n$ 個の頂点を持つ有向非巡回グラフ $G$ と整数 $k \leq n$ が与えられたとします。全ての頂点を覆う互いに頂点が重ならない最大 $k$ 個の路の集合を計算する効率の良いアルゴリズムを説明してください。
2. $n$ 個の頂点を持つ有向非巡回グラフ $G$ と整数 $k \leq n$ が与えられ、辺に (負でもあり得る) 重みが付いているとします。全ての頂点を覆う互いに頂点が重ならない最大 $k$ 個の路の集合であって重みの和が最小なものを計算する効率の良いアルゴリズムを説明してください。
答えのアルゴリズムの実行時間は小さな定数 $c$ に対して $O(n^{k+c})$ である必要があります。また一つの頂点の路としての重みは $0$ です (十一章で (a) に対するより効率的なアルゴリズムを見ます)。
プロのロッククライマー Kris は全米選手権に出場します。選手権ではクライミングウォールにあるホールドを使うときに許されている動きが審判によって設定され、そのルールの下で一番多くホールドを使った選手の勝ちです。

クライミングウォールには $n$ 個のホールドがあり、Kris には $(x, y)$ の形をした組が $m$ 個与えられ、各組が $y$ 番目のホールドから $x$ 番目のホールドへの移動が許されていることを表します。Kris は点数を最大化するために、なるべく長い許された移動の列を見つける必要があります。Kris は最初と最後のホールドを選ぶことができます。また同じホールドは何度でも使うことができますが、点数が増えるのは最初に訪れたときだけです。
1. 入力を表す自然なグラフを定義します。このグラフが DAG であることが保証されているときに、Kris のクライミング問題を解くアルゴリズムを説明、解析してください。
2. 入力グラフに制約が無い場合に Kris のクライミング問題を解くアルゴリズムを説明、解析してください。
両方のアルゴリズムの出力は Kris の獲得できる最大得点としてください。
$n$ 個の銀河を結ぶ $m$ 個の銀河間テレポートウェイがあります。各テレポートウェイは二つの銀河を結んでいて、双方向に使うことができます。テレポートウェイを管理している会社は自分たちにとても有利な料金体系を敷いています: 自分の銀河から遠ざかる方向に向かうテレポートは無料なのですが、自分の銀河に近づく方向のテレポートはとても高額です。

Judy は大学のサバティカルを使った旅行でできる限り多くの銀河を訪れることにしました。旅行は彼女の銀河から始まります。旅行代を浮かせるために、最後の一回を除いた全てのテレポートは自分の銀河から遠ざかる方向にしたいと彼女は考えています。
1. Judy が訪れることができる銀河の数の最大値を計算するアルゴリズムを説明、解析してください。アルゴリズムの入力はテレポートウェイのネットワークを表す $n$ 個の頂点と $m$ 個の辺を持つ無向グラフ $G$ と Judy の住む銀河を表す整数 $1 \leq s \leq n$、そして銀河 $s$ から各銀河への距離を表す配列 $D[1..n]$ です。
2. ❤ 銀河をめぐる旅行に出かけようとしたちょうどそのとき、Judy は宇宙宝くじに当選し、自分の銀河に向かうテレポート一回分の金額を手に入れました。これで Judy は自分の銀河に向かうテレポートを二回行えることになります。Judy が訪れることができる銀河の数の最大値を計算するアルゴリズムを説明、解析してください。同じ銀河を二回訪れても構いませんが、訪れた銀河の数に数えるのは最初の一回だけです。
ドクターと River Song は有向非巡回グラフ $G$ を使ったゲームをすることになりました。$G$ には一つのソース $s$ と一つのシンク $t$ が含まれます¹。

二人のプレイヤーは $G$ の頂点に駒を置きます。ゲームの開始時ドクターの駒はソース頂点 $s$ に、River の駒はシンク頂点 $t$ にあり、プレイヤーはドクターから始めて交互に駒を動かします。各ターンでドクターは有向辺に沿って駒を進め、River は有向辺の逆方向に駒を勧めます。

二つの駒が一つの頂点で出会ったら River の勝ち ("Hello, Sweetie!") で、River の駒が $s$ に着くかドクターの駒が $t$ に着いたらドクターの勝ちです。

二人のプレイヤーが完璧にプレイしたときに誰がゲームに勝つかを判定するアルゴリズムを説明、解析してください。つまり、River がどんな動きをしたとしてもドクターが勝つことができるならアルゴリズムの出力は "Doctor" であり、ドクターがどんな動きをしたとしても River が勝つことができるならアルゴリズムの出力は "River" です (なぜこの二つの可能性しかないのでしょうか？)。アルゴリズムの入力はグラフ $G$ です。
♣ ❤ $x = x_{1} x_{2} \ldots x_{n}$ を適当な有限アルファベット上の $n$ 文字の文字列とし、$A$ を同じアルファベットに対する $m$ 状態の決定性有限状態機械とします。
1. $A$ によって受理される $x$ の部分列で最長のものの長さを求めるアルゴリズムを説明、解析してください。例えば、$A$ が言語 $\texttt{({\color{maroon}AR})}^{\ast}$ を受理する機械で $x = \texttt{\color{maroon}{\underline{A}B\underline{R}AC\underline{A}DAV\underline{R}A}}$ である場合、アルゴリズムの出力は文字列 $\texttt{\color{maroon}{ARAR}}$ に対応する $4$ です。
2. $A$ によって受理される $x$ の超配列で最短のものの長さを求めるアルゴリズムを説明、解析してください。例えば、$A$ が言語 $\texttt{({\color{maroon}ABCDR})}^{\ast}$ を受理する機械で $x = \texttt{\color{maroon}{ABRACADABRA}}$ である場合、アルゴリズムの出力は文字列 $\texttt{\color{maroon}\underline{AB}CD}$$\texttt{\color{maroon}\underline{RA}B\underline{C}}$$\texttt{\color{maroon}DR\underline{A}BC}$$\texttt{\color{maroon}\underline{D}R\underline{AB}}$$\texttt{\color{maroon}CD\underline{RA}}$$\texttt{\color{maroon}BCDR}$ に対応する $25$ です。
アルゴリズムの解析は入力文字列の長さ $n$ と有限状態機械の状態数 $m$ とアルファベット $\Sigma$ のサイズを使って行ってください。
全ての動的計画法の問題が有向非巡回グラフにおける最適路を見つける問題として表せるわけではありません。しかし全ての動的計画法のアルゴリズムはその問題に応じたなんらかの依存グラフを帰りがけ順で処理します。
1. 有向非巡回グラフ $G$ が与えられ、各頂点に探索の時に鍵となる数値が保存されているとします。二分探索木となっている $G$ の部分グラフで最大のものを見つけるアルゴリズムを説明、解析してください。
2. 有向非巡回グラフ $G$ と二つの頂点 $s, t$ が与えられたとします。$s$ から $t$ への路の数を計算するアルゴリズムを説明してください (算術計算は $O(1)$ 時間でできるとしてください)。
3. $G$ を次の条件を満たす有向非巡回グラフとします:
  - $G$ には一つのソース $s$ といくつかのシンク $t_{1}, t_{2}, \cdots, t_{k}$ がある。
  - 各辺 $v \rightarrow w$ には $0$ か $1$ の重み $p(v \rightarrow w)$ がある。
  - シンクでない全ての頂点 $v$ について、$v$ を始点とする辺の重みの和は $1$ である。つまり、$\sum_{v} p(v \rightarrow w) = 1$ が成り立つ。
  重み $p(v \rightarrow w)$ は $G$ における $s$ から $t$ へのランダムウォークを定義します: シンクでない頂点 $v$ についたとき、歩行者は確率 $p(v \rightarrow w)$ で $v \rightarrow w$ をたどります (全ての確率は互いに独立です)。全ての添え字 $i$ について、このランダムウォークが $t_{i}$ にたどり着く確率を計算するアルゴリズムを説明、解析してください (算術計算は $O(1)$ 時間でできるとしてください)。

$s$ と $t$ というラベルは the Untempered Schism と the Time Vortex、あるいは the Shining World of the Seven Systems (Gallifrey としても知られる) と Trenzalore、あるいは Skaro と Telos、あるいは "Something else Timey-wimey" の頭文字をとったものです。とにかくすごく複雑なので、気にしないでください。^[return]