行きがけ順と帰りがけ順

根付き木に対する深さ優先探索によって行きがけ順 (preorder) および帰りがけ順 (postorder) が定義できることは知っているはずです。同じような走査順序は任意の (連結であるとは限らない) 有向グラフに対しても定義できます。次のようにカウンターを使います:

procedure \(\texttt{DFSAll}\)(\(G\))

\(\color{#2D2F91}{\mathit{clock} \leftarrow 0}\)

for 頂点 \(v\) do

\(v\) の印を消す

for 頂点 \(v\) do

if \(v\) に印が付いていない then

\(\mathit{clock} \leftarrow\)\(\texttt{DFS}\)(\(v, \mathit{clock}\))

procedure \(\texttt{DFS}\)(\(v, \mathit{clock}\))

\(v\) に印を付ける

\(\color{red}{\mathit{clock} \leftarrow \mathit{clock} + 1;\ \mathit{v.pre} \leftarrow \mathit{clock}}\)

for \(v \rightarrow w\) の形をした辺 do

if \(w\) に印が付いていない then

\(\mathit{parent}(w) \leftarrow v\)

\(\texttt{DFS}\)(\(w\))

\(\color{green}{\mathit{clock} \leftarrow \mathit{clock} + 1;\ \mathit{v.post} \leftarrow \mathit{clock}}\)

図 6.3

深さ優先探索を使った行きがけ順と帰りがけ順の定義

一般的な深さ優先探索に対して \(\textsc{Preprocess}\), \(\textsc{PreVisit}\), \(\textsc{PostVisit}\) を次のように定義しても同じアルゴリズムを得ることができます:

procedure \(\texttt{Preprocess}\)(\(G\))

\(\color{#2D2F91}{\mathit{clock} \leftarrow 0}\)

procedure \(\texttt{PreVisit}\)(\(v\))

\(\color{red}{\mathit{clock} \leftarrow \mathit{clock} + 1}\)

\(\color{red}{\mathit{v.pre} \leftarrow \mathit{clock}}\)

procedure \(\texttt{PostVisit}\)(\(v\))

\(\color{green}{\mathit{clock} \leftarrow \mathit{clock} + 1}\)

\(\color{green}{\mathit{v.post} \leftarrow \mathit{clock}}\)

このアルゴリズムは \(v\) を再帰スタックに積んだときに \(\mathit{v.pre}\) を代入し (そして \(\mathit{clock}\) を進め)、再帰スタックから \(v\) を取り出したときに \(\mathit{v.post}\) を代入し (そして \(\mathit{clock}\) を進め) ます。任意の二つの頂点 \(u, v\) に対して、二つの区間 \([\mathit{u.pre}, \mathit{u.post}]\) と \([\mathit{v.pre}, \mathit{v.post}]\) は重ならないか、そうでなければ片方がもう一方に含まれることが示せます。さらに、\([\mathit{u.pre}, \mathit{u.post}]\) が \([\mathit{v.pre}, \mathit{v.post}]\) を含むことは \(\textsc{DFS}(v)\) が \(\textsc{DFS}(u)\) の実行中に呼ばれることと同値で、さらに親をたどるポインタの集合からできる森において \(u\) が \(v\) の祖先であることとも同値です。

\(\textsc{DFSAll}\) がグラフの全ての頂点にラベルを付け終わると、\(\mathit{v.pre}\) は頂点の行きがけ順序 (preordering) を定義し、\(\mathit{v.post}\) は頂点の帰りがけ順序 (postordering) を定義します¹。いくつかの自明な例外を除けば、グラフは複数の行きがけ順序と複数の帰りがけ順序を持ちます。\(\textsc{DFS}\) がある頂点から出る辺を考えるときの順番や \(\textsc{DFSAll}\) が頂点を考えるときの順番によって順序が変化するためです。

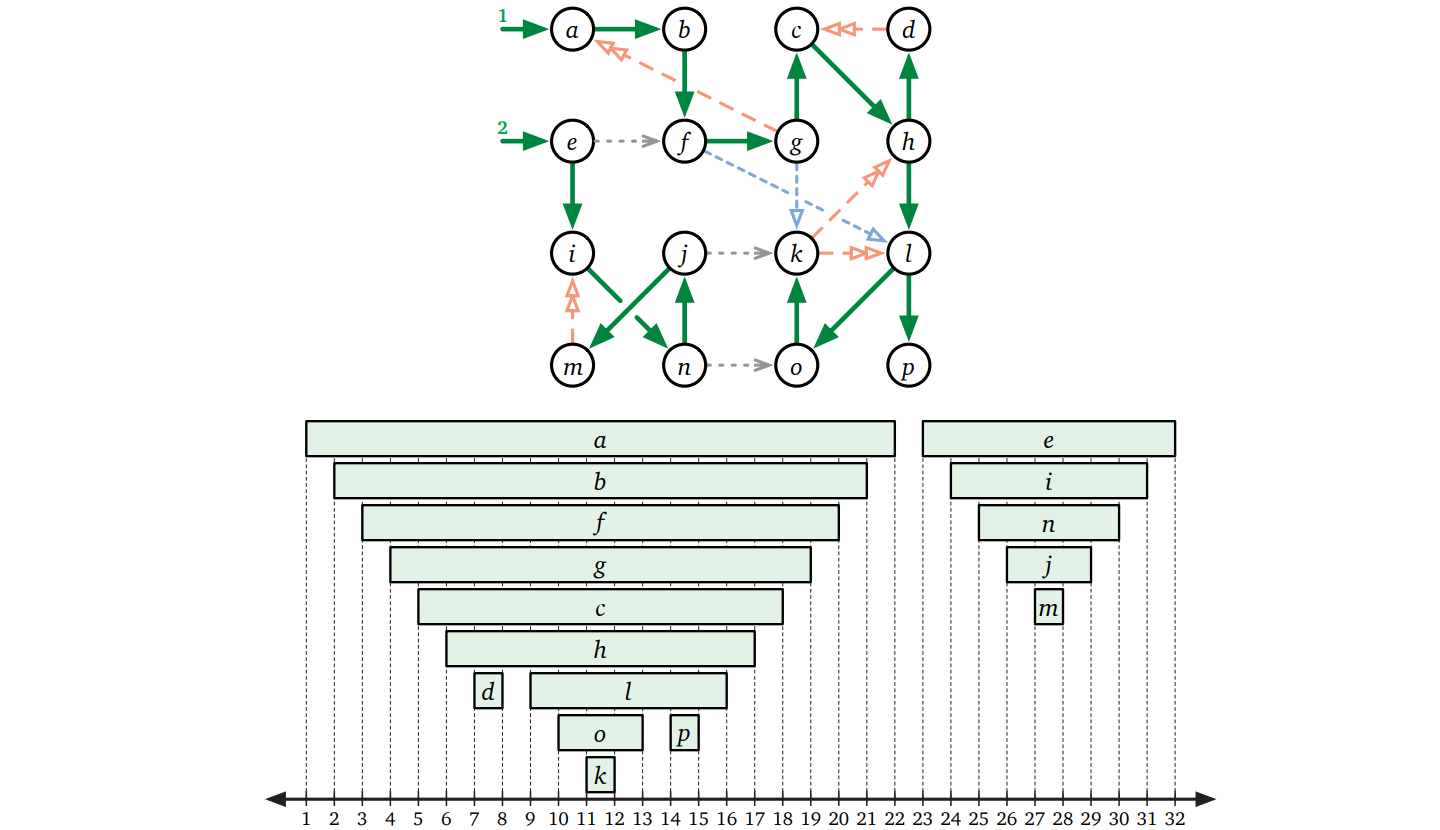
有向グラフの深さ優先探索と、それに対応する頂点のアクティブな区間。この探索によって行きがけ順序 <strong>abfgchdlokpeinjm</strong> と帰りがけ順序 <strong>dkoplhcgfbamjnie</strong> が定義される。森の辺が実践で表されている。破線の意味は次の図を参照。 — 図 6.4

有向グラフの深さ優先探索と、それに対応する頂点のアクティブな区間。この探索によって行きがけ順序 **abfgchdlokpeinjm** と帰りがけ順序 **dkoplhcgfbamjnie** が定義される。森の辺が実践で表されている。破線の意味は次の図を参照。

この章の残りの部分では、\(\mathit{v.pre}\) を \(\pmb{v}\) の開始時刻 (あるいは少しくだけて「\(v\) が始まるとき」)、\(\mathit{v.post}\) を \(\pmb{\mathit{v}}\) の終了時刻 (あるいは少しくだけて「\(v\) が終わるとき」)、開始時刻と終了時刻の間の区間をアクティブな区間 (あるいは少しくだけて「\(v\) がアクティブな間」) と呼ぶことにします。

頂点と辺の分類

\(\textsc{DFSAll}\) の実行中、入力グラフの各頂点 \(v\) は次の状態のうちどれかにあります:

未処理: \(\textsc{DFS}(v)\) が呼ばれていない。つまり \(\mathit{clock} < \mathit{v.pre}\) が成り立つ。
アクティブ: \(\textsc{DFS}(v)\) が呼ばれ、まだ返っていない。つまり \(\mathit{v.pre} \leq\) \(\mathit{clock} < \mathit{v.post}\) が成り立つ。
処理済: \(\textsc{DFS}(v)\) が返った。つまり \(\mathit{v.post} \leq \mathit{clock}\) が成り立つ。

開始時刻と終了時刻が再帰スタックのプッシュとプルに対応していることから、頂点がアクティブなのはそれが再帰スタックにあるときです。またアクティブな頂点の集合に含まれる全ての頂点を通る \(G\) の有向路が常に存在することが示せます。

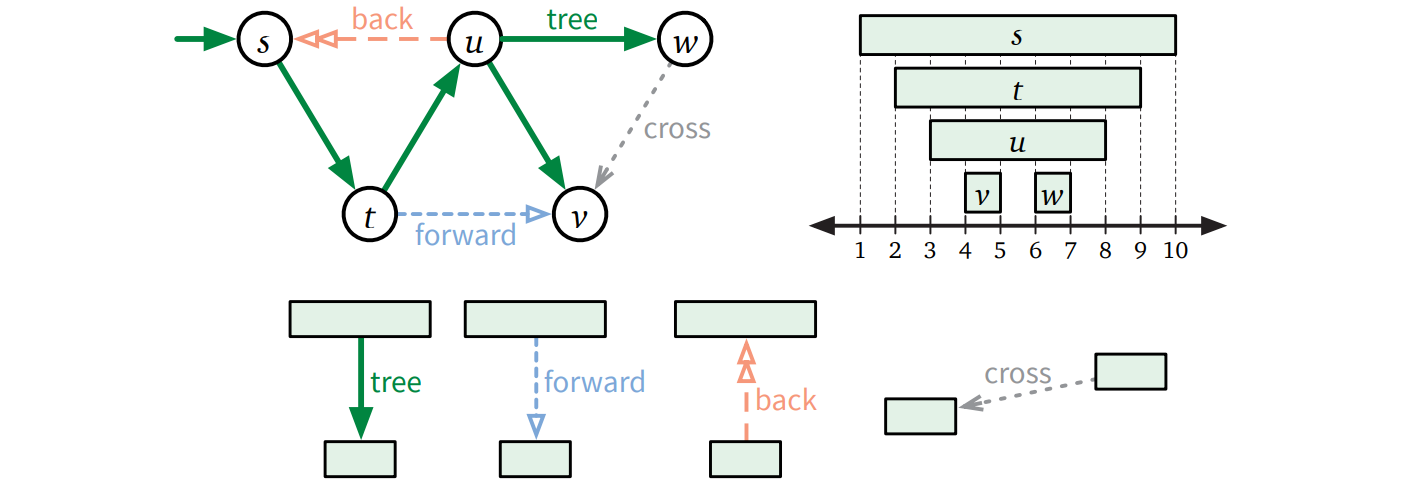
入力グラフの辺 \(u \rightarrow v\) は、\(u, v\) のアクティブな区間がどう交わるかによって次の四つに分類できます:

\(\textsc{DFS}(u)\) が始まったときに \(v\) が未処理な場合、\(\textsc{DFS}(v)\) は \(\textsc{DFS}(u)\) の実行中に直接または追加の再帰呼び出しを挟んで間接的に呼ばれる。どちらの場合においても、\(u\) は \(v\) の真の先祖であり、\(\mathit{u.pre} < \mathit{v.pre} < \mathit{v.post} < \mathit{u.post}\) が成り立つ。
- \(\textsc{DFS}(u)\) が \(\textsc{DFS}(v)\) を直接呼ぶ場合、\(u = \mathit{v.parent}\) であり、このような \(u \rightarrow v\) を木辺 (tree edge) と呼ぶ。
- そうでなければ、\(u \rightarrow v\) を前方辺 (forward edge) と呼ぶ。
\(\textsc{DFS}(u)\) が始まった時に \(v\) がアクティブな場合、\(v\) は既に再帰スタックに載っている。したがって逆の包含関係 \(\mathit{v.pre} < \mathit{u.pre} < \mathit{u.post} < \mathit{v.post}\) が成り立つ。加えて \(G\) は \(v\) から \(u\) に向かう有向路を持つ。この条件を満たす辺 \(u \rightarrow v\) を後方辺 (backward edge) と呼ぶ。
\(\textsc{DFS}(u)\) が始まった時に \(v\) が処理済みのとき、直ちに \(\mathit{v.post} < \mathit{u.pre}\) が分かる。この条件を満たす辺 \(u \rightarrow v\) を交差辺 (cross edge) と呼ぶ。
最後に、四つ目の順序 \(\mathit{u.post} < \mathit{v.pre}\) はあり得ない。

この辺の分類を下図に示します。ここでも、実際の辺の分類は \(\textsc{DFSAll}\) が頂点を考える順番と \(\textsc{DFS}\) が各頂点から出る辺を考える順番で変化します。

命題 6.1 有向グラフ \(G\) の任意の深さ優先走査を一つ固定する。\(G\) の任意の二つの頂点 \(u, v\) について、次の命題は同値である。

深さ優先木において \(u\) が \(v\) の先祖である。
\(\mathit{u.pre} \leq \mathit{v.pre} < \mathit{v.post} \leq \mathit{u.post}\)
\(\textsc{DFS}(v)\) が呼ばれたとき、\(u\) はアクティブである。
\(\textsc{DFS}(u)\) が呼ばれる直前、\(u\) から \(v\) への路であって \(u, v\) を含む全ての頂点が未処理のものが存在する。

証明まず深さ優先木において \(u\) が \(v\) の先祖だと仮定する。定義により \(u\) から \(v\) への路 \(P\) が存在する。路の長さに関する帰納法により、\(\mathit{u.pre} \leq\) \(\mathit{w.pre} <\) \(\mathit{w.post} \leq \mathit{u.post}\) が \(P\) に含まれる全ての頂点 \(w\) について成り立ち、したがって \(\textsc{DFS}(u)\) が呼ばれたとき \(P\) の全ての頂点は未処理である。前述の不等式から \(\mathit{u.pre} \leq\) \(\mathit{v.pre} < \) \(\mathit{v.post} \leq \mathit{u.post}\) が成り立ち、さらに \(\textsc{DFS}(v)\) が実行されているとき \(u\) はアクティブである。

親へ向かうポインタが再帰呼び出しを意味していることから、\(\mathit{u.pre} \leq\) \(\mathit{v.pre} <\) \(\mathit{v.post} \leq\) \(\mathit{u.post}\) は \(u\) が \(v\) の先祖であることを意味する。

\(\textsc{DFS}(v)\) が呼ばれたとき \(u\) がアクティブならば、直ちに \(\mathit{u.pre} \leq\) \(\mathit{v.pre} <\) \(\mathit{v.post} \leq\) \(\mathit{u.post}\) が分かる。

最後に、深さ優先探索木において \(u\) が \(v\) の先祖でないと仮定する。\(u\) から \(v\) への路 \(P\) を固定し、\(x\) を \(P\) の頂点の中で \(u\) の子孫でない最初の頂点、\(w\) を \(P\) における \(x\) の前者とする。辺 \(w \rightarrow x\) が存在するので \(\mathit{x.pre} < \mathit{w.post}\) が成り立つ。また \(w\) が \(u\) の子孫であることから \(\mathit{w.post} < \mathit{u.post}\) であり、よって \(\mathit{x.pre} < \mathit{u.post}\) である。さらに \(x\) が \(u\) の子孫でないことから \(\mathit{x.pre} < \mathit{u.pre}\) が分かる。アクティブな区間同士が共通部分を持つとき、片方がもう一方を真に含むことから、\(u\) と \(x\) の区間について二つの可能性がある:

\(\mathit{u.post} < \mathit{x.post}\) の場合、\(\textsc{DFS}(u)\) が呼ばれたとき \(x\) はアクティブである。
\(\mathit{x.post} < \mathit{u.pre}\) の場合、\(\textsc{DFS}(u)\) が呼ばれたとき \(x\) は終了している。

つまり \(u\) から \(v\) への任意の路には \(\textsc{DFS}(u)\) が呼ばれた時点で未処理でない頂点が含まれる。 \(\Box\)

紛らわしいことに、この二つの順序は両方とも「深さ優先順序 (depth-ordering)」と呼ばれることがあります。あなたはこういうことをしないでください。^[return]