編集距離
二つの文字列の間の編集距離 (edit distance)とは、一方の文字列をもう片方と同じ文字列に変形するために必要となる、文字の挿入、削除、置換の最小回数です。例えば \(\color{maroon}{\texttt{FOOD}}\) は次のように \(\color{maroon}{\texttt{MONEY}}\) に変形できるので、\(\color{maroon}{\texttt{FOOD}}\) と \(\color{maroon}{\texttt{MONEY}}\) の間の編集距離が最大でも \(4\) であることが分かります: \[ {\color{maroon}\texttt{FOOD}} \rightarrow {\color{maroon}\texttt{MOOD}} \rightarrow {\color{maroon}\texttt{MOND}} \rightarrow {\color{maroon}\texttt{MONED}} \rightarrow {\color{maroon}\texttt{MONEY}} \]
この距離関数は暗号理論を研究していた Vladimir Levenshtein (ウラジミール・レーベンシュタイン) によって 1965 年に、音声認識を研究していた Taras Vintsyuk (タラス・ヴィンチュク) によって 1968 年に、そして生物学的配列を研究していた Stanisław Ulam (スタニスワフ・ウラム) によって 1972 年に、それぞれ独立に提案されました。そのため編集距離は Levenshtein 距離あるいは Ulam 距離と呼ばれることがあります (なぜか "Vintsyuk 距離" と呼ばれることはありません)。
二つの文字列を上下に並べて書くと編集距離を可視化できます。このとき上の単語に含まれる空白は文字の挿入を、下の単語に含まれる空白は文字の削除を、上下の文字が異なる列は文字の置換を表します。このように表すと、必要となる編集の回数は同じ文字が並んでいない列の数となります: \[ \begin{aligned} \color{maroon}{\texttt{FOO D}} \\ \color{maroon}{\texttt{MONEY}} \end{aligned} \]
\(\color{maroon}{\texttt{FOOD}}\) を \(\color{maroon}{\texttt{MONEY}}\) に 3 ステップで変形させるのが不可能なのはほとんど明らかなので、\(\color{maroon}{\texttt{FOOD}}\) と \(\color{maroon}{\texttt{MONEY}}\) の間の編集距離は \(4\) となります。しかし残念ながら、一般の場合について編集の列が最短であるかどうかを判定するのはこれほど簡単ではありません。例えば次の表記からは二つの文字列 \(\color{maroon}{\texttt{ALGORITHM}}\) と \(\color{maroon}{\texttt{ALTRUISTIC}}\) の間の編集距離が最大で \(6\) なことが分かりますが、これが最小でしょうか? \[ \begin{aligned} \color{maroon}{\texttt{AL TRUISTIC}} \\ \color{maroon}{\texttt{ALGOR I THM}} \end{aligned} \]
再帰的な構造
編集距離を計算する動的計画法を使ったアルゴリズムを作るには、まず問題を再帰的に定式化する必要があります。編集距離を可視化するために文字列を上下に並べて書く今説明した表記には、「最適な小構造 (optimal substructure)」という重要な特徴があります。つまり、二つの文字列に対する最適な表記が手に入った場合、最後の列を取り除くと、残りの列が二つの接頭語に対する最小の編集回数を表すということです。この証明は簡単な帰納法です: もし二つの接頭語の間の編集距離がもっと小さかった場合、その編集の列を表す表記に取り除いた列を戻すことで、元の二つの文字列に対する編集距離よりも短い編集の列を作れますが、これは編集距離が最短の編集の列の長さであることに矛盾します。よって最後の列で何が起こるべきかが分かれば、あとは再帰の妖精が残りの最適な編集列を求めてくれます。
言い換えると、求めようとしている編集の列は右から左に並んだ編集操作によって表されます (右から左という順序に特別な意味はありません)。そして編集距離問題を解くとは、一列ごとに次の編集操作が何かを決断していくことに対応します。決断の列の途中では、二つの文字列の接尾部分が上下に並びます:

編集のコストは同じ文字が並んでいない列の数でしかないので、これからの決断にこれまでの決断が影響することはありません。これからの決断を決めるのは、まだ編集されていない接頭部分だけです。

よって \(A[1..m]\) と \(B[1..n]\) という文字列に対する編集距離問題を、次のように定式化できます: 「任意の添え字 \(i, j\) について、接頭辞 \(A[1..i]\) と \(B[1..j]\) の間の編集距離を \(\pmb{\mathit{Edit}(i, j)}\) とする。\(\mathit{Edit}(m, n)\) を求めよ」
再帰方程式
\(i, j\) を整数とします。\(A[1..i]\) と \(B[1..j]\) の最後の列に対する最適な編集を求めたい状況では、ちょうど三つの選択肢があります。
-
挿入: 最後の列の下段が空となる。このとき編集距離は \(\mathit{Edit}(i, j - 1) + 1\) である。 \(+1\) がこの挿入を表し、\(\mathit{Edit}(i, j - 1)\) が残りの部分の最適な編集回数を表す。

-
削除: 最後の列の上段が空となる。このとき編集距離は \(\mathit{Edit}(i - 1, j) + 1\) である。 \(+1\) がこの削除を表し、\(\mathit{Edit}(i - 1, j)\) が残りの部分の最適な編集回数を表す。

-
置換: どちらの段にも文字が入る。二つの文字が異なるなら編集距離は \(\mathit{Edit}(i - 1, j - 1) + 1\) である。二つの文字が同じならばこの置換は何もしないので、編集距離は \(\mathit{Edit}(i - 1, j - 1)\) である。

この解析は \(i = 0\) または \(j = 0\) のときに上手く行かなくなりますが、この場合は直接処理した方が簡単です:
-
空文字列を \(j\) 文字の文字列に変形するには \(j\) 回の挿入が必要なので、\(\mathit{Edit}(0, j) = j\)
-
\(i\) 文字の文字列を空文字列に変形するには \(i\) 回の削除が必要なので、\(\mathit{Edit}(i, 0) = i\)
検算として、二つのベースケースが両方とも空文字列同士の編集距離を正しく \(0\) と計算することを確認しておきましょう!
以上の解析から、\(\mathit{Edit}\) 関数が次の再帰方程式を満たすと言えます: \[ \mathit{Edit}(i, j) = \begin{cases} i & \text{if } j = 0 \\ j & \text{if } i = 0 \\ \min \left\lbrace \begin{array}{c} \mathit{Edit}(i, j - 1) + 1 \\ \mathit{Edit}(i - 1, j) + 1 \\ \mathit{Edit}(i - 1, j - 1) + [A[i] \neq B[j]] \end{array} \right\rbrace & \text{それ以外} \end{cases} \]
動的計画法
再帰方程式ができたので、これから動的計画法を使ったアルゴリズムを作ります。おなじみの機械的なステップを踏みます。
-
小問題: 再帰的に解く小問題は二つの添え字 \(0 \leq i \leq m\) と \(0 \leq j \leq n\) で特定できる。
-
メモ化のためのデータ構造: よって \(\mathit{Edit}(i, j)\) が取りうる全ての値は二次元配列 \(\mathit{Edit}[0..m, 0..n]\) に格納できる。
-
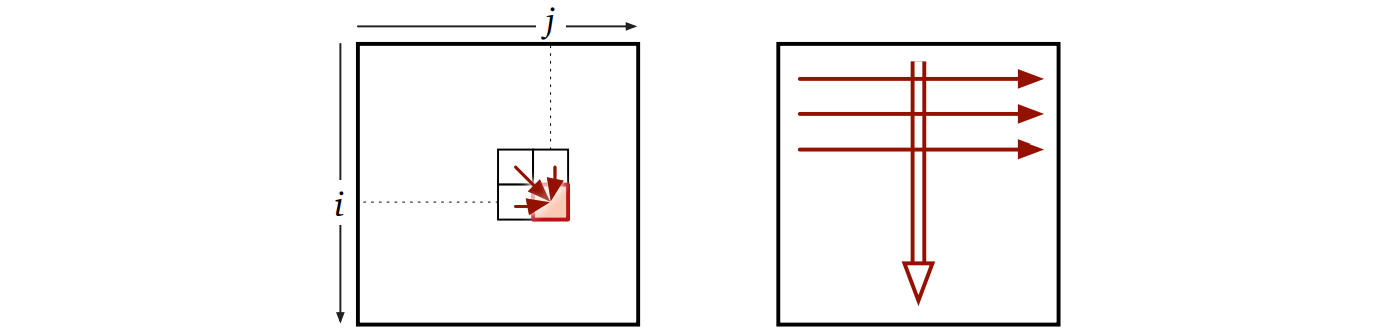
依存関係: \(\mathit{Edit}[i ,j]\) は隣り合った三つの要素 \(\mathit{Edit}[i - 1, j],\) \(\mathit{Edit}[i, j - 1],\) \(\mathit{Edit}[i - 1, j - 1]\) にのみ依存する。
-
評価順序: 配列を普通の列優先 (行は上から下、列は左から右) の順序で埋めていけば、各要素が依存する全ての値がその要素を計算するときまでに埋まる (条件を満たす評価順序はこれだけではないが、正しく動くので、これを使う)。
-
時間と空間: メモ化のためのデータ構造は空間を \(O(mn)\) だけ使う。 \(\mathit{Edit}[i, j]\) の計算はそれまでのメモが埋まっていれば \(O(1)\) でできるので、アルゴリズム全体の実行時間は \(\pmb{O(mn)}\) となる。
完成したアルゴリズムを次に示します:
procedure \(\texttt{EditDistance}\)(\(A[1..m], B[1..n]\))
for \(j \leftarrow 0\) to \(n\) do
\(\mathit{Edit}[0, j] \leftarrow j\)
for \(i \leftarrow 1\) to \(m\) do
\(\mathit{Edit}[i,0] \leftarrow i\)
for \(j \leftarrow 1\) to \(n\) do
\(\mathit{ins} \leftarrow \mathit{Edit}[i, j-1] + 1\)
\(\mathit{del} \leftarrow \mathit{Edit}[i-1, j] + 1\)
if \(A[i] = B[j]\) then
\(\mathit{rep} \leftarrow \mathit{Edit}[i-1, j-1]\)
else
\(\mathit{rep} \leftarrow \mathit{Edit}[i-1,j-1] + 1\)
\(\mathit{Edit}[i, j] \leftarrow \min \lbrace \mathit{ins},\ \mathit{del},\ \mathit{rep} \rbrace\)
return \(\mathit{Edit}[m, n]\)
このアルゴリズムは Robert Wagner (ロバート・ワグナー) と Michael Fischer (マイケル・フィッシャー) によって 1974 年に提案され、彼らのものとされることが最も多いです。しかしここでもエポニムに関するスティグラーの法則は働いていて、これと同じあるいはもっと一般的なアルゴリズムが 1968 年には Taras Vintsyuk によって、1970 年には N. G. Zagoruyko (G・G・ザゴルイコ) によって、 1972 年には David Sankoff (デイビット・サンコフ) によって、1974 年には Peter Sellers (ピーター・セラーズ) によってそれぞれ独立に発見され、他にも独立に発見したと思われる人物が何人かいます1。興味深いことに、ここにあげた研究者は誰一人として Levenshtein と Ulam に触れていません!
\(\color{maroon}{\texttt{ALGORITHM}}\) と \(\color{maroon}{\texttt{ALTRUISTIC}}\) に対してこのアルゴリズムを実行したときに出来上がるメモの表を次に示します。太字で書かれている部分は、注目している二つの文字が同じであることを表します。\(\color{maroon}{\texttt{ALGORITHM}}\) と \(\color{maroon}{\texttt{ALTRUISTIC}}\) の編集距離は本当に \(6\) でした!
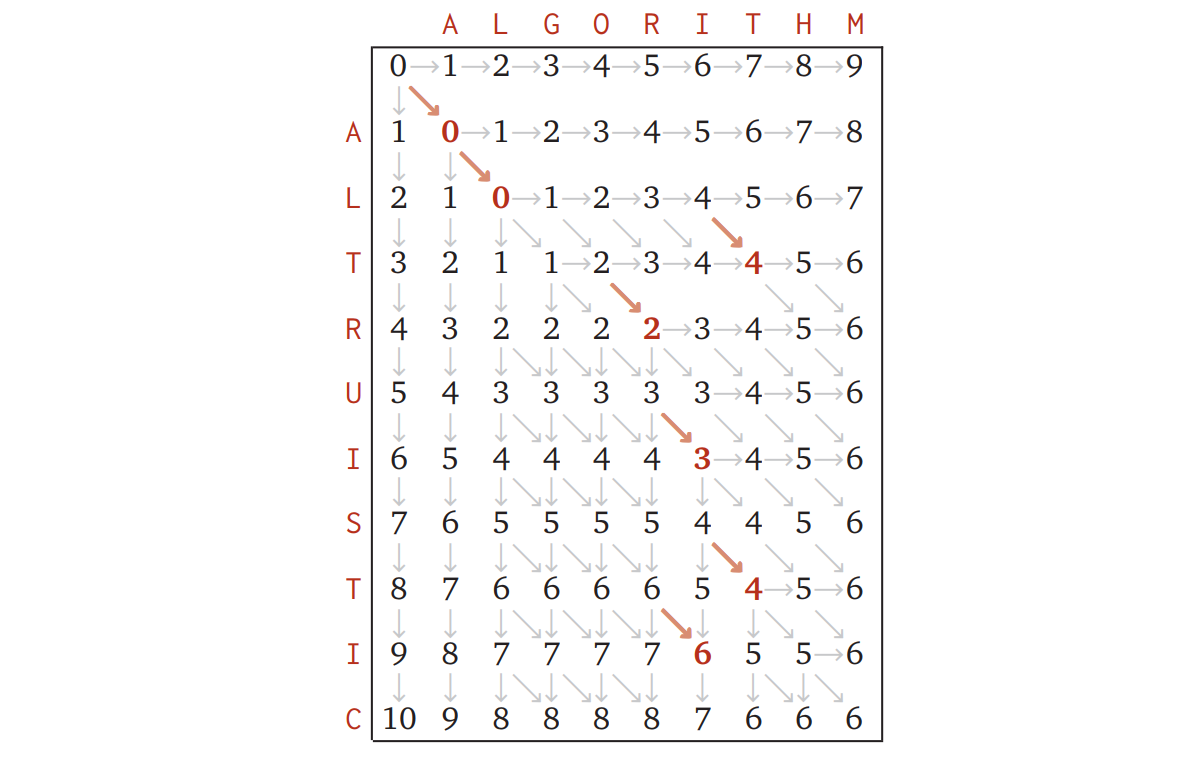
表の矢印を見れば各要素の一つ前の要素がどれかが分かるようになっており、矢印の向きは編集操作 (水平=削除, 垂直=挿入, 斜め=置換) を表します。赤くて太い斜めの矢印は二つの文字が同じであることで起こる "無料の" 置換であり、左上から右下への任意のパスが二つの文字列の間の最適な編集操作の列を表します。この例では左上から右下へのパスは三つあり、それぞれ以下の表記に対応します: \[ \begin{gathered} \color{maroon}{\texttt{ALTRUISTIC }} \\ \color{maroon}{\texttt{ALGORI THM }} \end{gathered} \] \[ \begin{gathered} \color{maroon}{\texttt{AL TRUISTIC}} \\ \color{maroon}{\texttt{ALGOR I THM}} \end{gathered} \] \[ \begin{gathered} \color{maroon}{\texttt{ALT RUISTIC}} \\ \color{maroon}{\texttt{ALGOR I THM}} \end{gathered} \]
\(\textsc{EditDistance}\) アルゴリズムはこの矢印の方向を計算したり表に保存したりしませんが、表の値が求まっていれば一つの矢印は \(O(1)\) 時間で計算できます。したがって表が全て埋まっていれば、最短の編集列は \(O(m+n)\) 時間を追加することで計算できます。
-
このアルゴリズムが Saul Needleman (ソール・ニードルマン) と Christian Wunsch (クリスチャン・ウンシュ) によって発見されたとされることがありますが、これは間違っています。また "Needleman-Wunsch のアルゴリズム" が、二つの文字列の最長共通部分列 (挿入と削除だけが許された時の編集距離) を計算する通常の動的計画法のアルゴリズムであると説明されることがありますが、これも間違っています。Needleman-Wunsch のアルゴリズムとは、重み付けされた、空白を許す最長共通部分列を \(O(m^{2}n^{2})\) 時間で計算するものであり、再帰方程式も異なります。 Sankoff は自身の \(O(mn)\) 時間のアルゴリズムが Needleman-Wunsch のアルゴリズムを改善したものであると明示的に説明していました。[return]