Mātrāvṛtta

人類が再帰処理を使った一番古い例は、2000 年以上前のインドにおける詩の歩格と韻律に関する研究に見ることができます。古典サンスクリット語の詩では、音節 (akṣara) を軽い (laghu) 音節と重い (guru) 音節の二つに区別していました。mātrāvṛtta (マトラブラッタ)、 mātrāchandas (マトラチャンダス) などと呼ばれる歩格の詩では各行が同じ数の拍 (mātrā) を持ち、軽い音節は一拍、重い音節は二拍の長さを持ちます。

mātrā-vṛtta に関するきちんとした研究をさかのぼると、紀元前 600 年から 200 年の間に韻律学者 Piṅgala (ピンガラ) によって書かれた Chandaḥśāstra (チャンダシャーストラ) という文献にたどり着きます。その文献で Piṅgala は、四拍の歩格が \(- \hspace{4pt} -,\ \)\(- \bullet \bullet,\ \)\(\bullet - \bullet,\ \)\(\bullet \bullet -,\ \)\(\bullet \bullet \bullet\ \bullet\) の五つしかないことを記しています (ここで \(-\) は重い音節を、\(\bullet\) は軽い音節を表します¹)。

与えられた拍が表現できる歩格の数を数える機械的な手続きについて Piṅgala は簡単なヒントを残しました²が、その問題がはっきりと表明されるのは約 1000 年後のことでした。紀元七世紀、インド人学者 Virahāṇka (ヴィラハーンカ) は Piṅgala の著作に対する注釈を執筆し、その中で \(n\) 拍で表現できる歩格の数が \(n-2\) 拍の歩格の数と \(n-1\) 拍の歩格の数の和であることを発見しました。現代的な表記を用いると、Virahāṇka が発見したのは \(n\) 拍の歩格の数 \(M(n)\) に関する次の再帰方程式です: \[ M(n) = M(n - 2) + M(n - 1) \] ベースケースの \(M(0) = 1\) (空の歩格が一つある) と \(M(1) = 1\) (一つの軽い音節からなる歩格が一つある) はすぐに分かります。

同じ再帰方程式は Virahāṇka から約 500 年後にヨーロッパで再発見されました。発見の場となったのは Leonardo of Pisa による 1202 年 の著作 Liber Abaci であり、これはヨーロッパ人による "algorism" に関する古い著作のうち最も影響力のあるものの一つです。エポニムに関するスティグラーの法則³に全く従って、Virahāṇka の再帰方程式を少し変更した次の式を、現代の私たちは Fibbonacci 数と呼んでいます。 \[ F_{n} = \begin{cases} 0 & \text{if } n = 0 \\ 1 & \text{if } n = 1 \\ F_{n-1} + F_{n-2} & \text{それ以外} \end{cases} \] 任意の \(n\) に対して \(M(n) = F_{n+1}\) が成り立ちます。

バックトラッキングは遅い

Fibbonacci 数の再帰的な定義から、\(F_{n}\) を計算する再帰的なアルゴリズムがすぐに分かります。疑似コードを次に示します:

残念ながら、このナイーブなアルゴリズムはひどく遅いです。このことを確認してみましょう。このアルゴリズムが行う再帰呼び出し以外の処理は、一度の比較と (無いこともある) 一度の加算です。そこで \(T(n)\) を \(\textsc{RecFibo}(n)\) を計算するときに \(\textsc{RecFibo}\) が呼び出される回数とすると、この関数は次の再帰方程式を満たします: \[ \begin{aligned} T(0) & = 1 \\ T(1) & = 1 \\ T(n) & = T(n - 1) + T(n - 2) + 1 \end{aligned} \] この方程式は Fibonacci 数の定義にそっくりです！ 最初のいくつかの項を書き出すと、閉じた答え \(\pmb{T(n) = 2 F_{n+1} - 1}\) を予想でき、帰納法 (ヒント、ヒント) によって正しいことが確かめられます。よってこのアルゴリズムを使って \(F_{n}\) を計算するとおよそ \(2 F_{n}\) の時間がかかります。さらにこの本の範囲を超える手法⁴を使うと黄金比 (golden-ratio) と呼ばれる数 \(\phi = (\sqrt{5} + 1) / 2\) を使って \(F(n) = \Theta(\phi^{n})\) と書けることが分かるので、このアルゴリズムの実行時間は \(n\) に対して指数的です。

アルゴリズムの実行時間が指数的であることは、次のように直接確かめることもできます: \(\textsc{RecFibo}\) の再帰木を、葉が 0 か 1 で頂点が加算を表す二分木として表します。最終的な出力が \(F_{n}\) なので、\(\textsc{RecFibo}(1)\) を表す値が \(1\) の葉はちょうど \(F_{n}\) 個あります。簡単な帰納法による (ヒント、ヒント) 議論によって、\(\textsc{RecFibo}(0)\) がちょうど \(F_{n-1}\) 回呼ばれることが分かります (漸近表記を得るだけなら、\(\textsc{RecFibo}(0)\) が多くとも \(\textsc{RecFibo}(1)\) と同じ回数しか呼ばれないことを確認すれば十分です)。よって再帰木は \(F_{n} + F_{n-1} =\) \(F_{n+1} =\) \(O(F_{n})\) 個の葉を持ち、二分木全体の葉は \(2F_{n+1} - 1 =\) \(O(F_{n})\) 個と分かります。

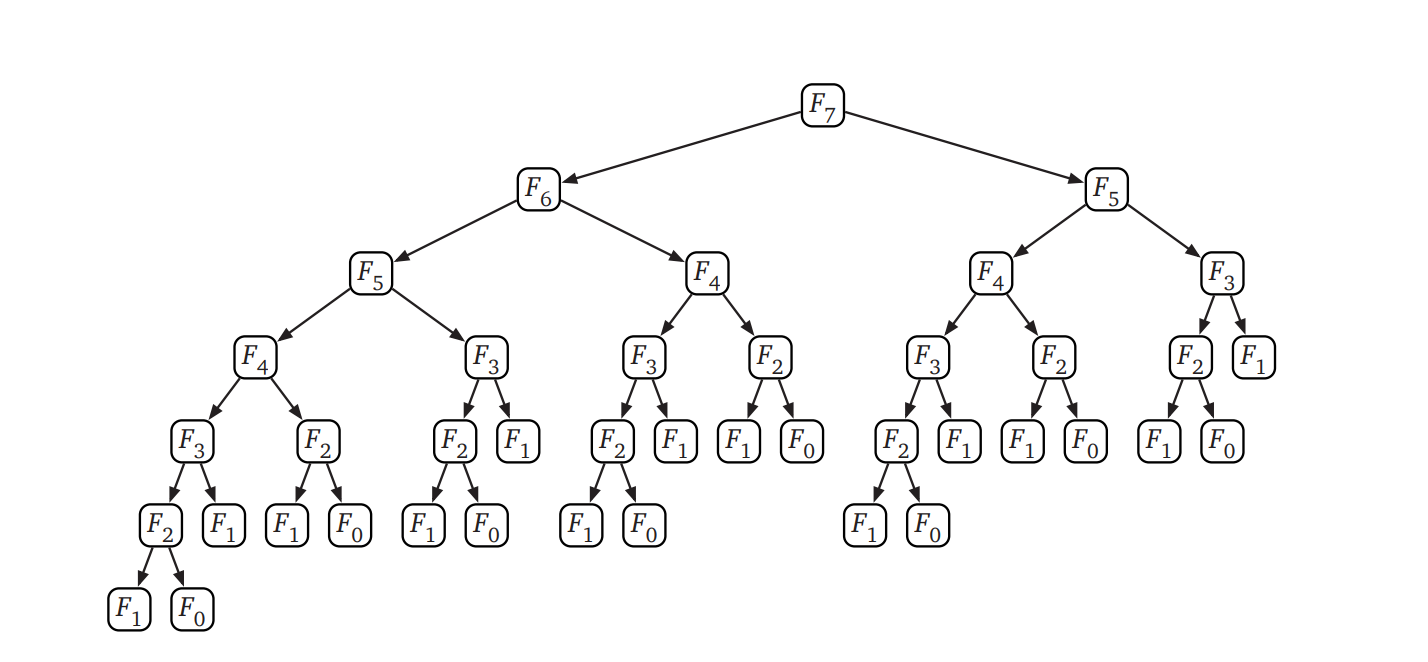
メモ化: 全てを覚える

この再帰的なアルゴリズムが遅い理由は明らかで、同じ Fibonacci 数を何度も何度も計算しているからです。\(\textsc{RecFibo}(n)\) を一度呼ぶと、再帰的な呼び出しによって \(\textsc{RecFibo}(n - 1)\) は一回、\(\textsc{RecFibo}(n - 2)\) は二回、\(\textsc{RecFibo}(n - 3)\) は三回、\(\textsc{RecFibo}(n - 4)\) は五回呼び出されます。一般的に言うと、\(0 \leq k \leq n\) について \(\textsc{RecFibo}(n - k)\) は \(F_{k-1}\) 回呼び出され、全ての呼び出しは Fibonacci 数を最初から計算します。

再帰呼び出しの結果を書き留めて後で同じ値が必要になった時にそれを参照するようにすれば、それだけでこの再帰的なアルゴリズムの実行速度を大きく向上させることができます。この最適化テクニックはメモ化 (memoization、r は付きません) と呼ばれます。メモ化は 1967 年に Donald Michie (ドナルド・ミッキー) よって提案されたとされることが多いですが、本質的に同じテクニックは 1959 年に Arthur Samuel (アーサー・サミュエル) によって提案されています⁵。

メモ化によって実行時間が小さくなるというのは明らかですが、正確にどれくらい小さくなるのでしょうか？ \(\textsc{MemFibo}\) の再帰呼び出しをたどって考えると、\(F[i]\) が埋まるのは \(F[i-1]\) が埋まったときだけなことが分かります。よって帰納法から配列 \(F[]\) は \(F[2], F[3], \ldots , F[n]\) と一番下から埋まることが示せます。Fibbonacci 数 \(F_{i}\) に関する再帰方程式の評価には再帰呼び出しにかかるコストを無視すれば定数時間しかかからず、問題の設定上 \(F_{i}\) は全ての添え字 \(i\) について計算される必要があるので、\(\textsc{MemFibo}(n)\) が実行する加算の回数は \(O(n)\) 回です。つまり、ナイーブな再帰的アルゴリズムと比べて指数的な高速化です！

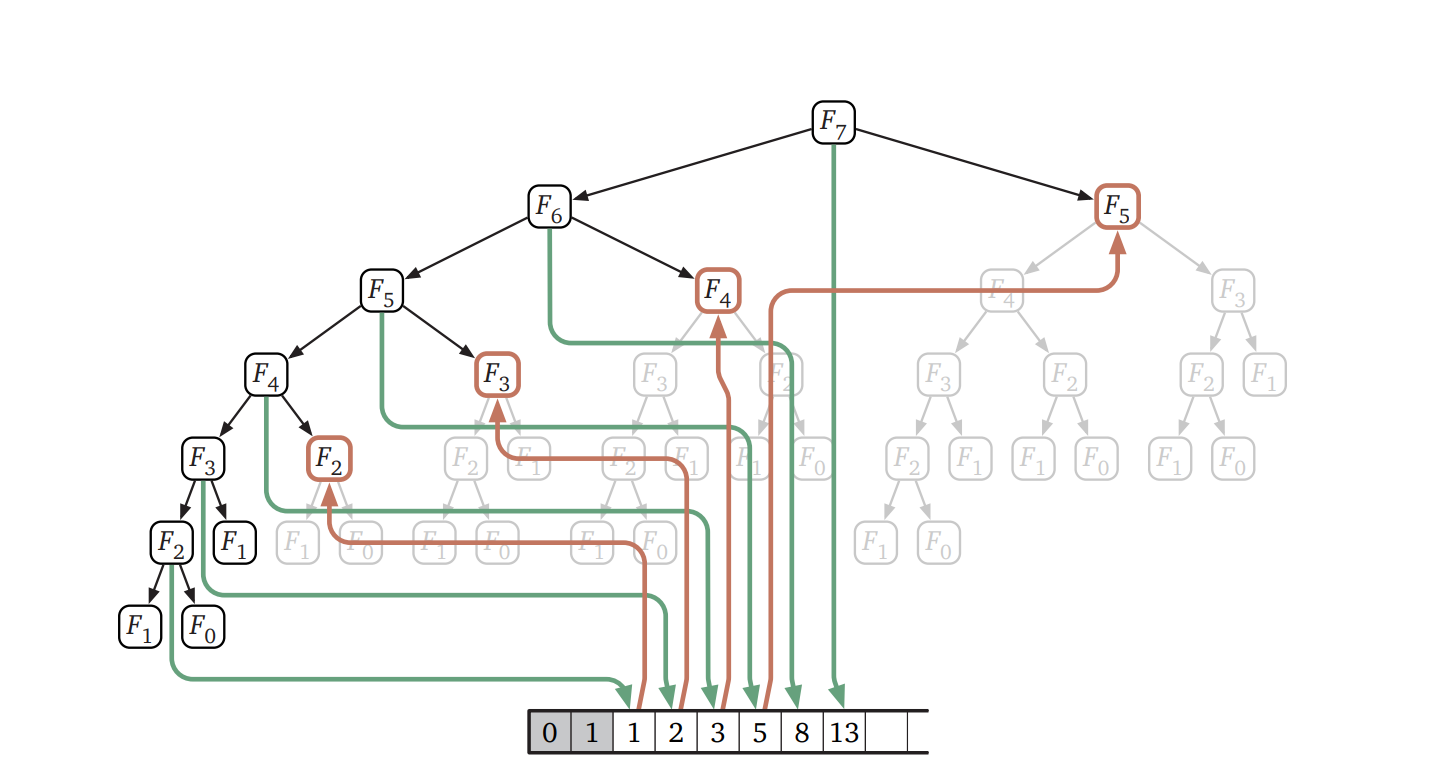
動的計画法: あらかじめ決められた順番で埋める

配列 \(F[]\) がどのように埋まるかが一度確認できてしまえば、メモ化を使う再帰的なアルゴリズムを変形して、for ループを使ってあらかじめ決められた順番で配列を埋めていくアルゴリズムを作ることができます。こうすれば、複雑な再帰呼び出しのせいで配列が埋まっていく順番が分かりにくくなっているアルゴリズム \(\textsc{MemFibo}\) を使わずにすみます。

実行時間は瞬時に分かります: \(\textsc{IterFibo}\) は \(\pmb{O(n)}\) 回の加算を行い、\(O(n)\) 個の整数を保存します。

これがこの本で出てくる最初の動的計画法 (dynamic programming) アルゴリズムです。動的計画法というパラダイムは 1950 年代の中頃に Richard Bellman (リチャード・ベルマン) によって定式化され、広まりました。彼はそのころランド研究所に勤めていましたが、彼がこのテクニックを最初に使った人物というわけでは決してありません。例えばちょうどいま紹介した Fibonacci 数をループを使って計算するアルゴリズムは Virahāṇka とその後のサンスクリット語の韻律学者に十二世紀には知られていましたし、Fibonacci も十三世紀初頭にはこのことに気付いていました⁶！

Bellman はこの古くから知られていた事実に対して「動的計画法」という名前を注意深く選ぶことで、数学の研究に見えるもの全てに反対していた軍部の上司にこのアルゴリズムの数学的な要素を隠すことに成功しました⁷。

ここで "program" という単語はコードを書くという意味ではなく、「計画を立てる (plan)」とか「スケジュールを立てる (schedule)」に近い古い意味で使われています。計画やスケジュールを立てるときに表を埋めることが多いためにこの単語が選ばれたのでしょう。例えばスポーツや映画館の program は重要なイベント (と広告) のスケジュールを立て、テレビ番組の program は利用可能な時間の枠を番組 (と広告) で埋め、学位 program は講義 (と広告) のスケジュールを立てます。空軍が Bellman たちに予算をつけて研究させたのは、訓練と兵站のスケジュール、つまり彼らが言うところの "program" を構築する方法でした。

"dynamic" という単語が使われたのは、最適化する処理が複数のステージと時間的な広がりを持っているためというのが理由の一つです。そしておそらくは、"dynamic" という単語が、第二次世界大戦後のアメリカが持っていた「未来には何でもできるようになる」という時代精神 (Futuristic Can-Do Zeitgeist™) に共鳴するバズワードであったためでもあります⁸。

Bellman の布教活動のおかげもあって、動的計画法は現代の経済学、ロボット工学、制御理論などの分野における多段階計画問題に対する標準的なツールとなりました。

全て覚え無くてもよい

動的計画法を使う問題の中には、計算の中間結果の全てを最後まで記憶しておく必要がないものも多くあります。例えば \(\textsc{IterFibo}\) では、配列の直近二つの要素だけを覚えておくようにすることで、空間消費量を大きく削減できます:

(このアルゴリズムは \(F_{-1} = 1\) というベースケースを使っています。これは通常の定義と異なりますが、\(\textsc{IterFibo}(0)\) が \(0\) を返すので以前の定義と矛盾しません。また空間消費量の抑制は実際のプログラムでとても重要になりますが、この本では空間の問題について深く議論しません)

1. モールス信号では "ツー" が "トン" の三倍の長さを持ち、"ツー" と "トン" 両方の後に空拍が続きます。そのため "トン" が laghu akṣara に、"ツー" が guru akṣara に対応すると言えます。実際、モールス信号には四つの mātrā からなる文字がちょうど五つ (M, D, R, U, H) あります。^[return]

2. Chandaḥśāstra には与えられた音節の数を持つ歩格を全て列挙する機械的な方法が二つ載っています。大まかに言うと数を二進法で表すことに対応し、一つは (ギリシャ人のように) 左から右に、もう一つは (エジプト人のように) 右から左に数を書いていきます。同じ部分にはこの他にも二乗を繰り返すことで \(2^{n}\) (\(n\) 音節に含まれる歩格の数) を計算する再帰的なアルゴリズム、そして二項係数 (\(k\) 個の軽い音節を含む、全体で \(n\) 音節の歩格の数) を計算する再帰的なアルゴリズムが含まれています (議論はありますが、おそらくは含まれています)。^[return]

3. 「実際の発見者の名前がつけられる科学的発見は存在しない」というのがスティグラー (Stigler) の法則です。この法則に名前が付けられた 1980 年の論文で、統計学者 Stephen Stigler (スティーブン・スティグラー) はこの法則を最初に発見したのは社会学者 Robert K. Merton (ロバート・K・マートン) であると冗談めかして書いています。しかし似たような発言はそれよりも前にされています: 1970 年代には Vladimir Arnol'd (ウラジーミル・アーノルド) によって (「発見が正しい人物に結びつけられることはほとんどない」)、1968 年には Carl Boyer (カール・ボイヤー) によって (「歴史の女神クレイオーは人名と定理を結び付けるときには気まぐれなことが多い」)、1917 年には Alfred North Whitehead (アルフレッド・ノース・ホワイトヘッド) によって (「重要なものはみな発見していない誰かによって言及されている」)、そして 1966 年にはなんと Stephen の父 George Stingler (ジョージ・スティグラー) によって (「定理に正しい人物の名前がつくことがもし万一あったら、特筆に値する」)。この本にはスティグラーの法則の例がたくさん出てきます。^[return]

4. バックトラッキングで生じる再帰方程式を解く方法については http://algorithms.wtf/ を見てください。^[return]

5. Michie は全てのプログラミング言語がサポートすべき抽象としてメモ関数 (memo function) を提案しました。メモ関数とは (通常の意味での) 関数 (rule) と辞書 (rote) という二つの要素からなり、ある入力に対する出力を初めて計算する場合には、出力を辞書にメモ (memorise、r が付く) してから値を返します。Michie はこのアイデアを、Samuel がチェッカーのゲーム木の再帰的な探索を高速化するために使った「暗記による学習 (rote learning)」 というテクニックから得ており、自身が行った一般的な提案を指して「プログラマーは好きな関数を "Samuelize" できるようになる」と説明しています (私が調べた限りでは、Michie 自身は "memoisation" という単語を一度も使っていません)。メモ化というテクニックは Samuel よりさらに前、1950 年に Claude Shannon (クロード・シャノン) が設計、構築した迷路を解く機械「テセウス (Theseus)」で使われています。^[return]

6. 動的計画法という一般的なテクニックは 1930 年代から 1940 年代にかけて独立に何度か発見されています。例えば Pierre Massé (ピエール・マス) はヴィシー政権のフランスにおいて、水力発電所の操業の最適化に動的計画法を使いました。John von Neumann (ジョン・フォン・ノイマン) と Oskar Morgenstern (オスカー・モルゲンシュテルン) は任意の二人対戦の完全情報ゲーム (例えばチェッカー) の勝者を判定するのに動的計画法を使いました。Alan Turing (アラン・チューリング) とその仲間たちはブレッチレー・パークで暗号を解読するときに同様の方法を使いました。Massé, von Neumann, Morgenstern が研究を最初に発表したのは 1944 年のことで、Bellman が "動的計画法" という言葉を思いつく 6 年前です。また Turing の "Banburismus" は 1980 年代中頃まで機密扱いでした。^[return]

7. Charles Erwin Wilson (チャールズ・アーウィン・ウィルソン) は 1953 年、長い間務めたゼネラルモーターズの社長としての職を離れて国防長官となりました。 "エンジンの Charlie" と知られた彼は国防総省を事業法人のようにすることを明確な目標とした改革を就任初年から開始し、予算を大幅に縮小しました。Bellman は Wilson について、1984 年の自伝でこう書いています:

   ワシントンには Wilson というとても興味深い紳士がいた。国防長官だった彼は、"研究" という単語に病理学的な恐怖と憎悪を抱いていた。私は "病理学的な" という言葉を軽々しく使っているつもりはない。彼の前で "研究" という単語を使おうものなら、彼の態度は一変して、顔は真っ赤になって、言葉遣いは乱暴になったものだ。彼が "数学" という単語についてどう感じていたか、簡単に想像が付くだろう。私がランド研究所で数学を研究していることを、どうにかして Wilson と空軍に隠さなければならないと私は感じていた。研究のタイトルは、そこで使う用語は、どうすればよいだろうか？

   ただし Bellman が最初に "動的計画法" という言葉を使ったのは 1952 年の Wilson が就任する数か月前なので、この話は少し装飾されています。^[return]

8. ...あるいは Charles Atlas による有名なエクササイズ番組に対して 1928 年に Charles Roman がつけた象徴的な名前 "Dynamic Tension" にかけただけかもしれません。^[return]