最適二分探索木

前章で最後に考えたのは最適二分探索木の問題でした。入力は探索のためのソートされた鍵 \(A[1..n]\) と頻度 \(f[1..n]\) であり、\(f[i]\) が \(A[i]\) に対する探索の回数を表します。出力は入力の鍵に対する二分探索木であって全ての探索の合計時間を最小にするものです。

頻度を表す配列 \(f\) を固定し、\(A[i..k]\) の最適探索時間を \(\mathit{OptCost}(i,k)\) とすると、次の再帰方程式が成り立つことを前章で見ました: \[ \mathit{OptCost}(i, k) = \begin{cases} 0 & \text{if } i > k \\ \displaystyle \sum_{j=i}^{k}f[j] + \min\limits_{i \leq r \leq k} \left \lbrace \begin{array}{l} \mathit{OptCost}(i, r-1) \\ \ + \mathit{OptCost}(r+1, k) \end{array} \right \rbrace & \text{それ以外} \end{cases} \] これから何をするのか想像がつくと思いますが、まずは和をどうにかします。

添え字の組 \(i,k\) (\(i \leq k\)) に対して、 鍵 \(A[i..k]\) に対応する頻度の合計を \(F(i, k)\) で表すことにします: \[ F(i, k) := \sum_{j=i}^{k}f[j] \] この関数は次の単純な再帰方程式を満たします: \[ F(i, k) := \begin{cases} f[i] & \text{if } i = k \\ F(i, k - 1) + f[k] & \text{それ以外} \end{cases} \] \(F(i, k)\) がとりうる全ての値は \(O(n^{2})\) 時間で計算できます。計算には、もちろん、動的計画法を使います。何度も使ってきた機械的なステップを踏めば、次のアルゴリズムとなります:

このアルゴリズムは初期化処理として利用します。\(F\) を初期化しておけば、再帰方程式を次のように単純化できます: \[ \mathit{OptCost}(i, k) = \begin{cases} 0 & \text{if } i > k \\ \displaystyle F[i, k] + \min\limits_{i \leq r \leq k} \left \lbrace \begin{array}{l} \mathit{OptCost}(i, r-1) \\ \ + \mathit{OptCost}(r+1, k) \end{array} \right \rbrace & \text{それ以外} \end{cases} \] さあ、準備は整いました。

• 小問題: 再帰的な小問題は二つの整数 \(i, k\) (\(1 \leq i \leq n + 1\), \(0 \leq k \leq n\)) で特定できる。

• メモ化: \(\mathit{OptCost}\) が取り得る値は二次元配列 \(\mathit{OptCost}[1..n+1, 0..n]\) に格納できる (実際に使われるのは \(j \geq i - 1\) を満たす \(\mathit{OptCost}[i,j]\) だけだが、気にしない)。

• 依存関係: \(\mathit{OptCost}[i, k]\) は全ての \(i\leq j \leq k\) について \(\mathit{OptCost}[i, j-1]\) と \(\mathit{OptCost}[j+1, k]\) に依存している。言い換えれば、表の任意の要素は下と左にある全ての要素に依存している:

  

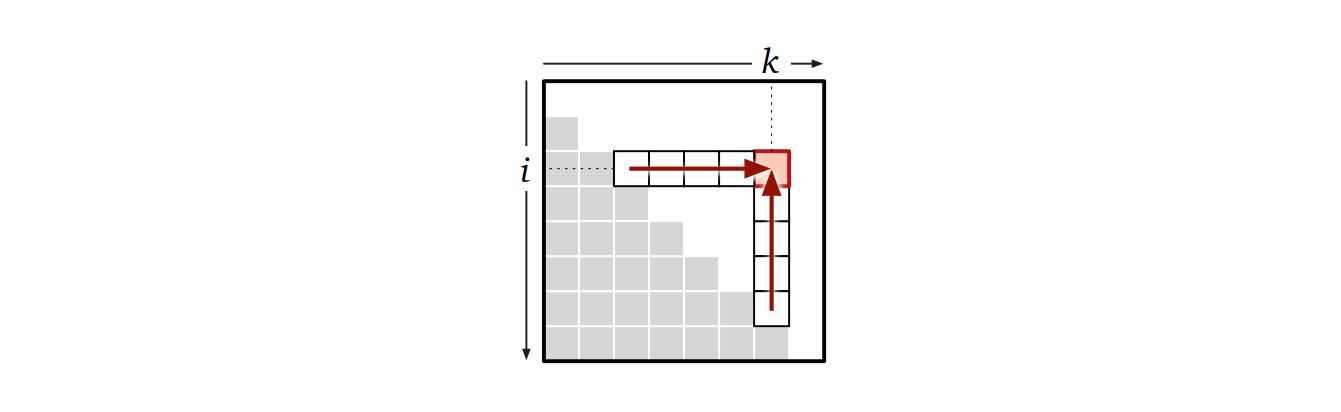
  依存する全ての値が計算されていると仮定すれば、\(\mathit{OptCost}[i,k]\) は次のサブルーチンで計算できる:

  procedure \(\texttt{ComputeOptCost}\)(\(i,k\))

  \(\mathit{OptCost}[i,k] \leftarrow \infty\)

  for \(r \leftarrow i\) to \(k\) do

  \(\mathit{tmp} \leftarrow \mathit{OptCost}[i, r-1] + \mathit{OptCost}[r+1,k]\)

  if \(\mathit{OptCost}[i,k] > \mathit{tmp}\) then

  \(\mathit{OptCost}[i,k] \leftarrow \mathit{tmp}\)

  \(\mathit{OptCost}[i,k] \leftarrow \mathit{OptCost}[i,k] + F[i,k]\)

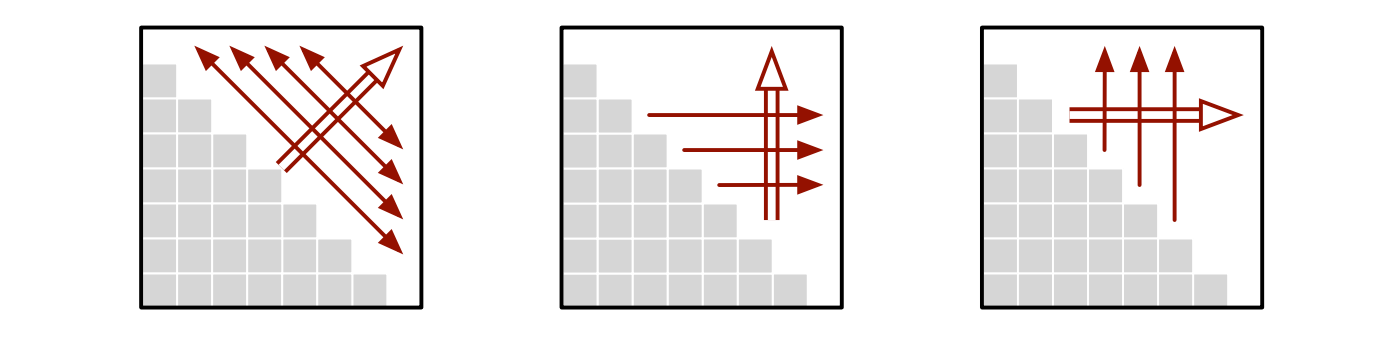
• 評価順序: 配列を埋めるのに使える順序は少なくとも三つはある。多くの生徒が最初に思いつくのは、ベースケース \(\mathit{OptCost}[i, i-1]\) から初めて対角線ごとに \(\mathit{OptCost}[1,n]\) に向かって埋めていくというものである:

  procedure \(\texttt{OptimalBST}\)(\(f[1..n]\))

  \(\texttt{InitF}\)(\(f(1..n)\))

  for \(i \leftarrow 1\) to \(n+1\) do

  \(\mathit{OptCost}[i,i-1] \leftarrow 0\)

  for \(d \leftarrow 0\) to \(n-1\) do

  for \(i \leftarrow 1\) to \(n - d\) ⟨⟨他の順序でもよい⟩⟩ do

  \(\texttt{ComputeOptCost}\)(\(i, i+d\))

  return \(\mathit{OptCost}[i,n]\)

  行優先で行を左からに右、列を下から上という順序、あるいは列優先で列を下から上、行を左から下という順序でも配列を埋めることができる:

  procedure \(\texttt{OptimalBST2}\)(\(f[1..n]\))

  \(\texttt{InitF}\)(\(f(1..n)\))

  for \(i \leftarrow n+1\) downto \(1\) do

  \(\mathit{OptCost}[i,i-1] \leftarrow 0\)

  for \(j \leftarrow i\) to \(n\) do

  \(\texttt{ComputeOptCost}\)(\(i, j\))

  return \(\mathit{OptCost}[i,n]\)

  procedure \(\texttt{OptimalBST3}\)(\(f[1..n]\))

  \(\texttt{InitF}\)(\(f(1..n)\))

  for \(j \leftarrow 0\) to \(n+1\) do

  \(\mathit{OptCost}[i,i-1] \leftarrow 0\)

  for \(i \leftarrow j\) downto \(1\) do

  \(\texttt{ComputeOptCost}\)(\(i, j\))

  return \(\mathit{OptCost}[i,n]\)

  三つの評価順序を図示すると以下のようになる。二重の矢印が外側のループを表し、一重の矢印が内側のループを表す。両方向の矢印はそのループの評価順序がどんなものでも構わないことを示す。

  

• 時間と空間 メモ化のためのデータ構造は空間を \(O(n^{2})\) だけ使う。どの評価順序を選んだとしても \(\mathit{OptCost}[i,k]\) の計算には \(O(n)\) 時間が必要なので、アルゴリズム全体の実行時間は \(\pmb{O(n^{3})}\) となる。

これまでの動的計画法を使ったアルゴリズムと同じように、消費空間と実行時間の上限は元の再帰方程式から見積ることもできます: \[ \mathit{OptCost}(i, k) = \begin{cases} 0 & \text{if } i > k \\ \displaystyle F[i, k] + \min\limits_{i \leq r \leq k} \left \lbrace \begin{array}{l} \mathit{OptCost}(i, r-1) \\ \ + \mathit{OptCost}(r+1, k) \end{array} \right \rbrace & \text{それ以外} \end{cases} \] \(\mathit{OptCost}\) 関数は二つの引数を取り、そのどちらもおおよそ \(n\) 個の異なる値を取るので、サイズが \(O(n^{2})\) のデータ構造が必要になると予想できます。また再帰方程式の本質的な部分には三つの変数 (\(i,k,r\)) があり、それぞれがおおよそ \(n\) 個の異なる値を取るので、全ての値を計算するには \(O(n^{3})\) の時間がかかると予想できます。