貪欲アルゴリズム

重要なのは、みなさん、貪欲は良いということです。貪欲であれば万事が上手く行く。貪欲であることは正しい。貪欲であれば物事は明確になり、道は開かれ、発展精神の本質が手に入る。命、金、愛、知識、全ての物事に対する貪欲さが、人類をここまで発展させました。そして貪欲さは、いいですか、Telbar Paper を救うだけではなく、機能不全に陥っているもう一つの企業 USA をも救うのです。

――Gordon Gekko [Michael Douglas], Wall Street (1987)

人間が抱えるどんな問題にも必ず簡単な答えがある ――

きちんとしていて、もっともらしくて、間違った答えが。

――H. L. Mencken, "The Divine Afflatus", New York Evening Mail (November 16, 1917)

テープへのファイルの保存

磁気テープ¹に $n$ 個のファイルを保存したいとします。テープに保存したファイルは後でユーザーが読み込みますが、テープからのファイルの読み込みはディスクからの読み込みのようにはいきません。磁気テープを読み込むときには、まず目的のファイルがあるところまでテープを送る必要があるからです。 $L[1..n]$ でファイルの長さを表すことにして、$i$ 番目のファイルの長さが $L[i]$ だとします。ファイルが $1$ から $n$ という順番で保存されていたとすると、$k$ 番目のファイルにアクセスするコストは次の式で表されます: \[ \mathit{cost}(k) = \sum_{i=1}^{k} L[i] \] $k$ 番目のファイルを読むには $k$ 番目までのファイルを送らなくてはいけないということが、この関数で表されています。それぞれのファイルに対する探索の頻度が同じだと仮定すれば、ランダムなファイルに対する探索コストの期待値を求められます: \[ E[\mathit{cost}] = \sum_{k=1}^{n} \frac{\mathit{cost}(k)}{n} = \sum_{k=1}^{n} \sum_{i=1}^{k} \frac{L[i]}{n} \]

テープ上のファイルの順番を変えると、各ファイルへのアクセスコストが変化し、読み込みが高速になるファイルもあれば遅くなるファイルもあります。この結果、探索コストの期待値も変化するはずです。つまり、$\pi(i)$ でテープで $i$ 番目に保存されているファイルの添え字を表すことにすると、置換 $\pi$ のコストの期待値は次の式で表されます: \[ E[\mathit{cost}(\pi)] = \sum_{k=1}^{n}\sum_{i=1}^{k} \frac{L[\pi(i)]}{n} \] このコストの期待値を最小化したい場合、どのような順番を使うべきでしょうか？直感的には答えは明らかです: 短いものから長いものに向かって並べるべきです。しかし直感というのは厄介な代物であり、この順番が正しいことを示すには ~~飛行機に乗り込んで核爆弾で全てを吹き飛ばす~~ 実際に証明しなければなりません！

命題 4.1 $E[\mathit{cost}(\pi)]$ は全ての $i$ で $L[\pi(i)] \leq L[\pi(i+1)]$ が成り立つとき最小となる。

証明ある添え字 $i$ で $L[\pi(i)] > L[\pi(i+1)]$ だったとする。簡単のため $a = \pi(i)$, $b = \pi(i+1)$ とする。 $a$ と $b$ を交換すると、$a$ へのアクセスコストは $L[b]$ 増え、$b$ へのアクセスコストは $L[a]$ 減る。よってこの交換で全体のコストの期待値は $(L[b] - L[a])/n$ だけ増える。 $L[b] < L[a]$ だったから、この交換によって元より良い順番が手に入っている。よって $L[\pi(i)] \leq L[\pi(i+1)]$ となっていない $i$ がある場合には、要素を交換することでコストを減少させることができる。したがって全ての $i$ で $L[\pi(i)] \leq L[\pi(i+1)]$ のときコストの期待値は最小となる。 $\Box$

これは私たちが最初に出会う貪欲アルゴリズム (greedy algorithm) です。ファイルアクセスにかかる全体コストの期待値を最小化するには、一番早くアクセスできるファイルを最初に書き込み、残りについて同じ処理を再帰的に行います。バックトラッキングも動的計画法もありません。ただ局所的に最良な選択肢を選んで盲目的に進むだけです。効率の良いソートアルゴリズムを使えば、順番を決める処理の実行時間は $O(n \log n)$ であり、この他にファイルへの書き込み時間がかかります。この貪欲アルゴリズムの証明では、他のアルゴリズムで作った順番が交換によって改善できてしまうことを示している点に注目してください。

このアイデアを推し進めてみましょう。新しい入力として各ファイルのアクセス頻度を表す $F[1..n]$ が加わり、ファイル $i$ はテープが使われなくなるまでにちょうど $F[i]$ 回アクセスされるとします。このときテープ上の全てのファイルに対するアクセスにかかる合計コストは次のようになります: \[ \begin{aligned} \Sigma \mathit{cost}(\pi) & = \sum_{k=1}^{n} \left(F[\pi(k)] \cdot \sum_{i=1}^{k} L[\pi(i)]\right) \\ & = \sum_{k=1}^{n} \sum_{i=1}^{k} (F[\pi(k)] \cdot L[\pi(i)]) \\ \end{aligned} \]

さてここでもファイルの順番を変えると探索にかかる合計コストが変化します。コストを最小化するには、どんな順番でファイルを保存すればよいでしょうか？ (この問題は最適二分探索木の問題と似ていると言うこともできるでしょう。しかしデータ構造とコスト関数がどちらも異なっているので、答えのアルゴリズムも異なっているはずです)

先ほど証明したのは、全てのファイルに対するアクセス頻度が等しいならファイルをサイズで昇順にソートすべきであるということです。またファイルのサイズ $L[i]$ が全て同じで頻度だけが異なっているならば、アクセス頻度で降順にソートすべきであるということは直感的に分かりますし、実際命題 4.1の証明を改変すれば証明も難しくありません。

ではサイズと頻度が両方とも変化したら？この場合、サイズと頻度の比 $L/F$ でソートすべきであるということが示せます:

命題 4.2 $\Sigma \mathit{cost}(\pi)$ は全ての $i$ に対して $\displaystyle \frac{L[\pi(i)]}{F[\pi(i)]} \leq \frac{L[\pi(i+1)]}{F[\pi(i+1)]}$ が成り立つとき最小となる。

証明ある添え字 $i$ で $L[\pi(i)]/F[\pi(i)] > L[\pi(i+1)]/F[\pi(i+1)]$ だったとする。簡単のため $a = \pi(i)$, $b = \pi(i+1)$ とする。 $a$ と $b$ を交換すると、$a$ へのアクセスコストは $L[b]$ 増え、$b$ へのアクセスコストは $L[a]$ 減る。よってこの交換で全体のコストの期待値は $(F[a] \cdot L[b] - F[b] \cdot L[a])/n$ だけ増える。ここで \[ \frac{L[a]}{F[a]} > \frac{L[b]}{F[b]} \Leftrightarrow L[b]F[a] - L[a]F[b] < 0 \] だから、この交換によって全体のコストは減少する。したがって、問題で示された順番に並んでいない任意の順番が与えられたとき、交換を行うことでその順番を改善できる。 $\Box$

講義のスケジューリング

次の例はもう少し複雑です。あなたは情報科学をドロップアウトして応用カオス理論を専攻することに決めたとします。応用カオス理論専攻では全ての講義が毎週同じ日に開校されており、この日は学生から「Soberday (素面日)」と呼ばれていました (興味深いことに、学部はこの名前を使いませんでした)。講義はそれぞれ異なった開始時刻と終了時刻を持ちます: 例えば AC 101 (トイレットペーパー景観設計 "Toilet Paper Landscape Architecture") は 10:27 pm に始まって 11:51 pm に終わり、AC 666 (終末の内在化 "Immanentizing the Eschaton") は 4:18 pm に始まって 4:22 pm に終わる、などです。できるだけ早く卒業したいあなたは、なるべく多くの講義を取りたいとします (応用カオス理論専攻の講義では履修さえすれば何もしなくても単位が取得できます)。大学の履修登録用コンピューターは時間が被っている講義を取らせてくれず、この "機能" を書き換えてくれる友達も見当たりません。取るべき講義はどれでしょうか？

きちんと言うと、講義の開始時刻と終了時刻が入った二つの配列 $S[1..n]$ と $F[1..n]$ が与えられ、ある実数 $M$ があって全ての $i$ に対して $0 \leq S[i] \leq F[i] \leq M$ が成り立つとします (例えば $M$ は Soberday の長さをピコ秒で表したものだったりします)。この問題で求めるのは $X \subset \lbrace 1,2,\ldots,n \rbrace$ であって任意の組 $(i,j) \in X$ に対して $S[i] > F[j]$ または $S[j] > F[i]$ が成り立つものの中で最大のものです。

この問題を図示すると以下のようになります。講義が長方形によって表され、$x$ 軸座標の左端と右端がそれぞれ講義の開始時刻と終了時刻を表します。垂直方向に重ならない長方形の部分集合で一番大きいものを見つけることが目標となります。

講義は取るか取らないかのどちらかなので、この問題には単純な再帰的解法があります。講義 $1$ が始まる前に終わる講義の集合を $B$ 、講義 $1$ が終わった後に始まる講義の集合を $A$ とします: \[ \begin{aligned} B & := \lbrace i \ | \ 2 \leq i \leq n \text{ かつ } F[i] < S[1] \rbrace \\ A & := \lbrace i \ | \ 2 \leq i \leq n \text{ かつ } F[1] < S[i] \rbrace \end{aligned} \] もし最適なスケジュールに講義 $1$ が含まれるならば、部分集合 $B$ と $A$ に対する最適スケジュールも全体の最適なスケジュールに含まれ、この二つの最適なスケジュールは再帰的に見つけることができます。もしそうでなくて最適なスケジュールに講義 $1$ が含まれないならば、全体の最適なスケジュールは $\lbrace 2, 3, \ldots, n \rbrace$ から再帰的に見つけることができます。この再帰的なアルゴリズムに対して動的計画法を適用すると実行時間が $O(n^{3})$ となりますが、ここでは詳細には踏み入りません。もっと速くできるからです²。

直感的に分かるのは、最初選ぶ講義はなるべく早く終わった方がその後に選択できる講義の選択肢が増えるということです。この直感を使うと、次の単純な貪欲アルゴリズムが作れます: 「全ての講義を終了時刻が早い順にチェックしていって、これまでの選択と矛盾しない講義を見つけたら、取る！」この貪欲アルゴリズムの動作を次に示します:

図 4.2

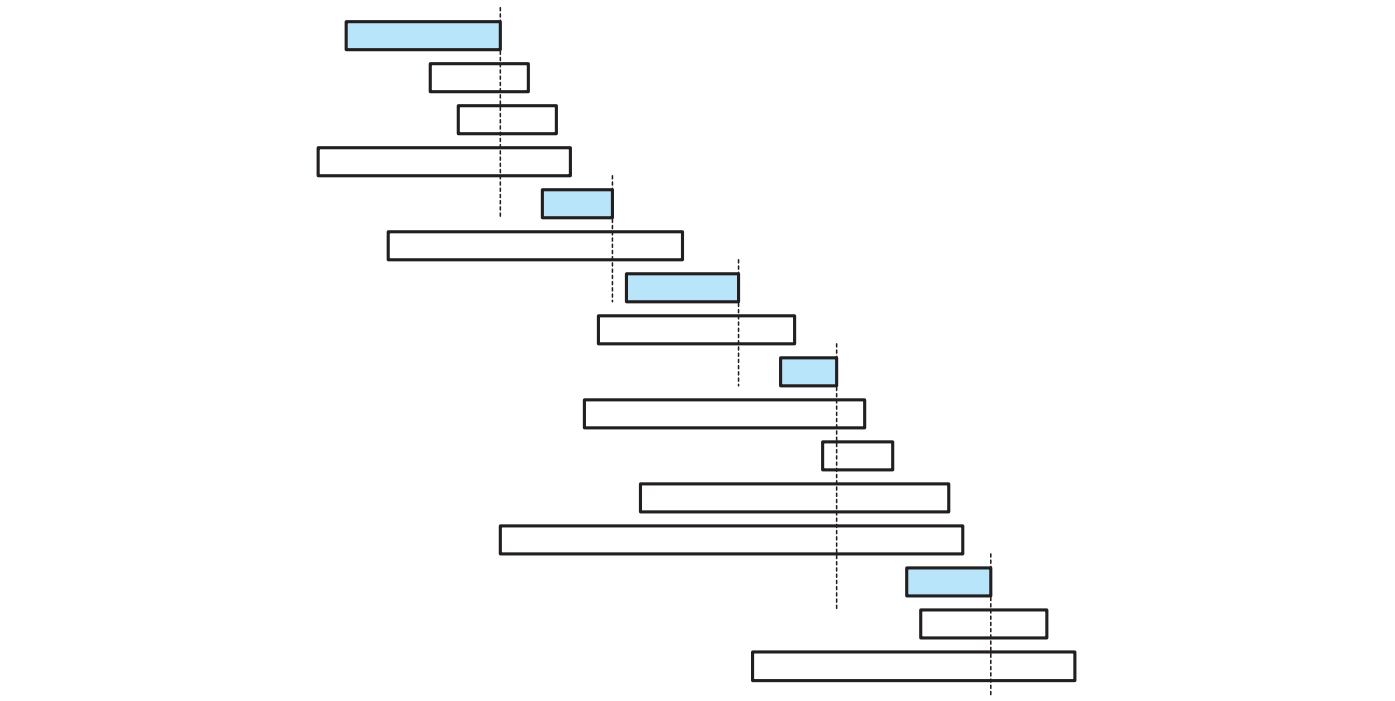
一つ前の図と同じ講義の集合を終了時刻でソートしたもの (水色の長方形が貪欲なスケジュールを表す)

このアルゴリズムをもう少しきちんと書くと次の疑似コードとなります (最初の行が理解できることを願います)。最初のソート後は線形時間で実行できる単純なループがあるだけなので、アルゴリズムの実行時間は最初のソートに支配されることになり、$O(n \log n)$ です。

procedure $\texttt{GreedySchedule}$($S[1..m], F[1..n]$)

$F$ をソートして $S$ をその結果に合うように並べ替える

$\mathit{count} \leftarrow 1$

$X[\mathit{count}] \leftarrow 1$

for $i \leftarrow 2$ to $n$ do

if $S[i] > F[X[\mathit{count}]]$ then

$\mathit{count} \leftarrow \mathit{count} + 1$

$X[\mathit{count}] \leftarrow i$

return $X[1..\mathit{count}]$

図 4.3

重ならない講義の最大集合を見つける貪欲アルゴリズム

$\textsc{GreedySchedule}$ が衝突しない最大のスケジュールを本当に計算することを示すには、テープのソートのときと同じような交換を使った議論 (exchange argument) を使います。ここで注意すべきなのは、示すべき命題が「貪欲なスケジュールが唯一の最大スケジュールである」ではない点です (上の二つの図を見比べてみてください！)。示すことができるのは「少なくとも一つの最適なスケジュールが貪欲アルゴリズムによって作られる」です。

命題 4.3 少なくとも一つの衝突しない最大スケジュールは一番早くに終了する講義を含む。

証明最初に終了する講義を $f$ とする。衝突しない最大スケジュールで $f$ を含まないものを $X$ 、$X$ で最初の講義を $g$ とする。 $f$ の終了時刻は $g$ よりも早いので、$f$ は $X \backslash \lbrace g \rbrace$ の任意の講義と衝突しない。よって $X^{\prime} = X \cup \lbrace f \rbrace \backslash \lbrace g \rbrace$ は衝突が起こらない。 $X^{\prime}$ は $X$ と同じサイズだから、同じく最大である。 $\Box$

アルゴリズム全体の正しさの証明には、私たちの旧友である帰納法の助けを借ります。

定理 4.4 貪欲なスケジュールは最適なスケジュールである。

証明 $f$ を一番早く終了する講義、$A$ を $f$ が終了した後に開始する講義の集合とする。一つ前の命題より最適なスケジュールで $f$ を含むものが存在する。 $f$ を含む最適なスケジュールは、$f$ と衝突しない講義すなわち $A$ に対する最適なスケジュールを持っていなければならない。貪欲なアルゴリズムは $f$ を選び、そして再帰法の仮定によって $A$ から最適なスケジュールを選ぶ。したがって貪欲なスケジュールは最適なスケジュールである。 $\Box$

この証明は帰納法を少し展開したほうが理解しやすいかもしれません。

証明貪欲アルゴリズムによって選ばれた講義を開始時間でソートして $\langle g_{1}, g_{2}, \ldots, g_{k} \rangle$ とする。衝突しない最大スケジュールであって開始時間でソートすると \[ S = \langle g_{1}, g_{2}, \ldots, g_{j-1}, c_{j}, c_{j+1}, \ldots, c_{m} \rangle \] と表せて、$c_{j}$ が $g_{j}$ と異なるものが存在すると仮定する (例えば $j=1$ とするとこのスケジュールは貪欲アルゴリズムが選ばない講義からスタートすることになる)。このスケジュールの構成から、$j$ 番目の貪欲な選択 $g_{j}$ はそれまでの講義 $g_{1}, g_{2}, \ldots, g_{j-1}$ と衝突しない。また $S$ は衝突しないことから、$c_{j}$ もそれまでの講義と衝突しない。さらに $g_{j}$ は $c_{j+1}, \ldots, c_{m}$ と衝突しないことも言えるので、変更したスケジュール \[ S = \langle g_{1}, g_{2}, \ldots, g_{j-1}, g_{j}, c_{j+1}, \ldots, c_{m} \rangle \] もまた衝突しないことが分かる (この議論は命題 4.3を一般化したものである。命題 4.3 では $j=1$ だった)。

帰納法によって、貪欲アルゴリズムが選択する講義を全て含む最適なスケジュール $\langle g_{1}, g_{2}, \ldots g_{k}, c_{k+1}, \ldots, c_{m} \rangle$ が存在することが言える。したがって $k=m$ でなければならない: もし貪欲アルゴリズムが選ぶ最初の $k$ 個の講義のどれとも衝突しない講義があるなら、貪欲アルゴリズムは $k$ 個より多い講義を選んでいなければならない！ $\Box$

共通するパターン

講義のスケジューリングに対する貪欲アルゴリズムの正しさの証明は、テープをソートするアルゴリズムの正しさの証明と同じ構造を持っています。つまり、帰納法を使った交換の議論 (exchange argument) です:

貪欲な解と異なる最適な解の存在を仮定する。
二つの解の "最初の" 違いを見つける。
最適な選択と貪欲な選択を交換しても解が悪くならないことを示す (良くならなくても構わない)。

この議論と帰納法を組み合わせると最適な解が貪欲な解を含むことを示すことができ、貪欲な解の性質からその二つが等しいことが言えます。スケジュールの問題のように、貪欲な解を狭義に改善する最適解が存在しないことを示すのに追加のステップが必要になることもあります。

Huffman 符号

二進符号 (binary code) は $0$ と $1$ からなる文字列 (符号) をアルファベットに対応させます。任意の符号が他の符号の接頭語になっていないとき、その二進符号は接頭独立 (prefix-free) であると言います (紛らわしいのですが、接頭独立な符号は接頭符号 (prefix code) と呼ばれることが多いです)。例えば 7 ビット ASCII コードと Unicode の UTF-8 はどちらも接頭独立な二進符号です。一方モールス信号は $\cdot$ と $-$ から構成されるものの、$\color{maroon}{\texttt{E}}$ (・) が $\color{maroon}{\texttt{I}}$ (・・) と $\color{maroon}{\texttt{S}}$ (・・・) と $\color{maroon}{\texttt{H}}$ (・・・・) の接頭語なので接頭独立ではありません³。

接頭独立な二進符号は葉が文字に対応する二分木を使って可視化でき、そのとき葉の文字に対する符号は根からその葉までの道によって表されます。つまり、根から葉へ向かう道をたどって行って、左に曲がったときに $0$ 、右に曲がったときに $1$ を書いていくと、出来上がる文字列がその文字に対する符号となります。ここから文字の符号の長さは対応する葉の深さと等しいことが分かります。二分符号木と二分探索木は外見では似ていますが、同じではありません。二分符号木では葉に対応する文字が並ぶ順番を全く気にしないからです。

$n$ 文字のアルファベットからなる文章を最小の符号で符号化したいとします。つまり、頻度を表す配列 $f[1..n]$ が与えられたときに、接頭独立な二進符号であって、次の式で表される符号化された文章の長さを最小にするものを求めたいということです: \[ \sum_{i=1}^{n} f[i] \cdot \mathit{depth}(i) \] このコスト関数は最適二分探索木のときに考えたものと全く同じですが、最適化問題における制約が異なっています。二分符号木では葉の順番に関する制約が全くありません。

MIT の Ph.D. 生だった David Huffman (デイヴィッド・ハフマン) は 1951 年、最適な符号を生成するための次の貪欲アルゴリズムを発見しました⁴:

Huffman: 頻度が最も低い二つの文字をマージし、残りは再帰的に処理する。

Huffman のアルゴリズムは例を使った方が分かりやすいでしょう。次に示すのは Lee Shallows (リー・サローズ) によって発見された、符号化を説明するのにとても都合がいい自己解説的 (self-descriptive) な文章です:⁵

This sentence contains three a's, three c's, two d's, twenty-six e's, five f's, three g's, eight h's, thirteen i's, two l's, sixteen n's, nine o's, six r's, twenty-seven s's, twenty-two t's, two u's, five v's, eight w's, four x's, five y's, and only one z.

解析を単純にするために 44 個のスペースと 19 個のアポストロフィと 19 個のコンマと 3 個のハイフンと 1 個のピリオドは無視して、さらに大文字だけを考えることにします。つまり、次の scriptio continua のような文字列だけを符号化の対象として考えるということです: \[ \begin{gathered} \color{maroon}{\texttt{THISSENTENCECONTAINSTHREEASTHREECSTWODSTWENTYSIXESFIVEFST}} \\ \color{maroon}{\texttt{HREEGSEIGHTHSTHIRTEENISTWOLSSIXTEENNSNINEOSSIXRSTWENTYSEV}} \\ \color{maroon}{\texttt{ENSSTWENTYTWOTSTWOUSFIVEVSEIGHTWSFOURXSFIVEYSANDONLYONEZ}} \end{gathered} \]

Sallow の文章に含まれる文字の頻度を表にすると次のようになります: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \color{maroon}{\texttt{A}} & \color{maroon}{\texttt{C}} & \color{maroon}{\texttt{D}} & \color{maroon}{\texttt{E}} & \color{maroon}{\texttt{F}} & \color{maroon}{\texttt{G}} & \color{maroon}{\texttt{H}} & \color{maroon}{\texttt{I}} & \color{maroon}{\texttt{L}} & \color{maroon}{\texttt{N}} & \color{maroon}{\texttt{O}} & \color{maroon}{\texttt{R}} & \color{maroon}{\texttt{S}} & \color{maroon}{\texttt{T}} & \color{maroon}{\texttt{U}} & \color{maroon}{\texttt{V}} & \color{maroon}{\texttt{W}} & \color{maroon}{\texttt{X}} & \color{maroon}{\texttt{Y}} & \color{maroon}{\texttt{Z}} \\ \hline 3 & 3 & 2 & 26 & 5 & 3 & 8 & 13 & 2 & 16 & 9 & 6 & 27 & 22 & 2 & 5 & 8 & 4 & 5 & 1 \\ \hline \end{array} \]

Huffman のアルゴリズムは最も頻度の低い二つの文字を選んでマージし、新しい文字とします。このとき頻度が同じ文字があるならどれを選んでも構いません。この例ではまず $\color{maroon}{\texttt{Z}}$ と $\color{maroon}{\texttt{D}}$ がマージされて新しく頻度 3 の文字 $\color{maroon}{\texttt{DZ}}$ となります。構築している木にこの新しい文字を表す頂点が加わり、$\color{maroon}{\texttt{Z}}$ と $\color{maroon}{\texttt{D}}$ がその頂点の子となります。このとき二つの子のどちらが $\color{maroon}{\texttt{Z}}$ でどちらが $\color{maroon}{\texttt{D}}$ かは出来上がる符号の最適性に関係ありません。マージの後 Huffman のアルゴリズムは頻度表を更新します: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \color{maroon}{\texttt{A}} & \color{maroon}{\texttt{C}} & \color{maroon}{\texttt{E}} & \color{maroon}{\texttt{F}} & \color{maroon}{\texttt{G}} & \color{maroon}{\texttt{H}} & \color{maroon}{\texttt{I}} & \color{maroon}{\texttt{L}} & \color{maroon}{\texttt{N}} & \color{maroon}{\texttt{O}} & \color{maroon}{\texttt{R}} & \color{maroon}{\texttt{S}} & \color{maroon}{\texttt{T}} & \color{maroon}{\texttt{U}} & \color{maroon}{\texttt{V}} & \color{maroon}{\texttt{W}} & \color{maroon}{\texttt{X}} & \color{maroon}{\texttt{Y}} & \color{maroon}{\texttt{DZ}} \\ \hline 3 & 3 & 26 & 5 & 3 & 8 & 13 & 2 & 16 & 9 & 6 & 27 & 22 & 2 & 5 & 8 & 4 & 5 & 3 \\ \hline \end{array} \]

再帰的に 19 回のマージを行うと 20 個の文字が一つの頂点にマージされ、マージされた様子を図示すると符号木となります。このアルゴリズムには何をするかを自由に選べる場面が何度もあるので、同じ頻度表に対する Huffman 符号はいくつも存在します。この例に対する Huffman 符号の一つを次に示します。葉でない頂点にはマージした文字の頻度の和が書かれています。例えば $\color{maroon}{\texttt{A}}$ に対する符号は $\color{#2D2F91}{\texttt{101000}}$ で、$\color{maroon}{\texttt{S}}$ に対する符号は $\color{#2D2F91}{\texttt{111}}$ です:

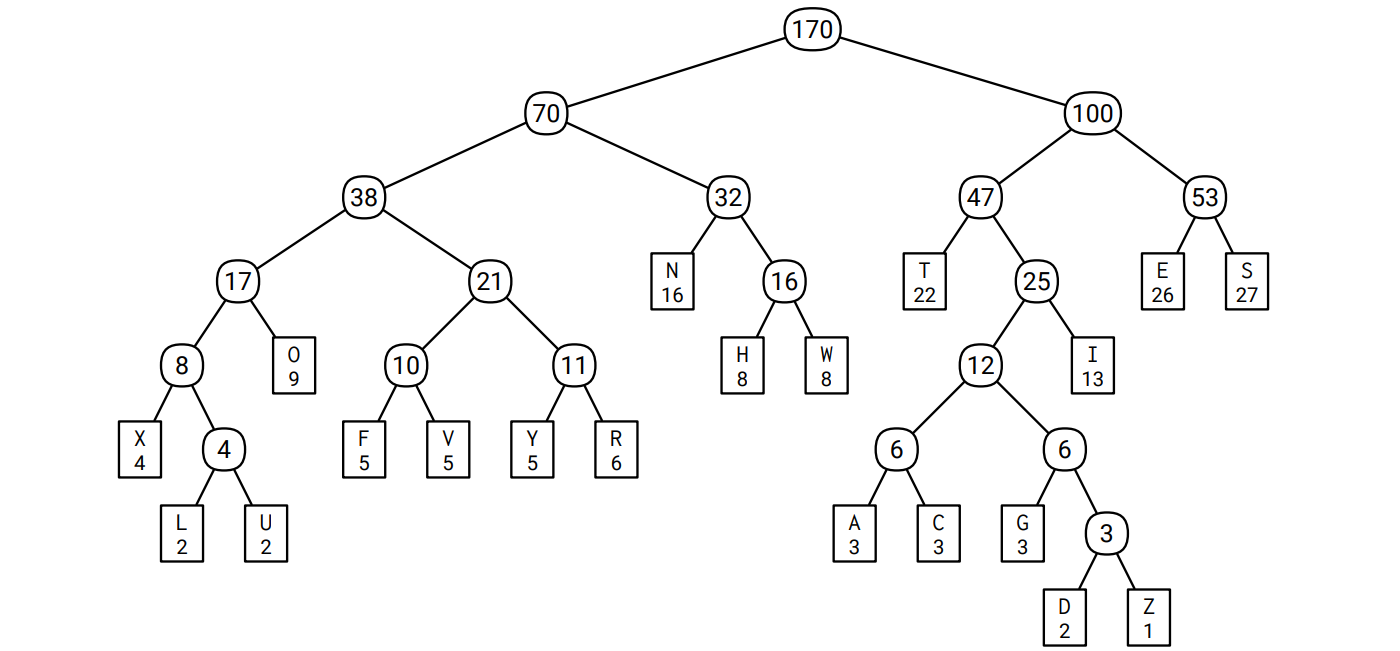
この Huffman 符号を使って Sallows の文章を符号化すると次のようになります: \[ \small \frac{\color{#2D2F91}\texttt{100}}{\color{#B52F1B}\texttt{T}} \frac{\color{#2D2F91}\texttt{0110}}{\color{#B52F1B}\texttt{H}} \frac{\color{#2D2F91}\texttt{1011}}{\color{#B52F1B}\texttt{I}} \frac{\color{#2D2F91}\texttt{111}}{\color{#B52F1B}\texttt{S}} \frac{\color{#2D2F91}\texttt{111}}{\color{#B52F1B}\texttt{S}} \frac{\color{#2D2F91}\texttt{110}}{\color{#B52F1B}\texttt{E}} \frac{\color{#2D2F91}\texttt{010}}{\color{#B52F1B}\texttt{N}} \frac{\color{#2D2F91}\texttt{100}}{\color{#B52F1B}\texttt{T}} \frac{\color{#2D2F91}\texttt{110}}{\color{#B52F1B}\texttt{E}} \frac{\color{#2D2F91}\texttt{010}}{\color{#B52F1B}\texttt{N}} \frac{\color{#2D2F91}\texttt{101001}}{\color{#B52F1B}\texttt{C}} \frac{\color{#2D2F91}\texttt{110}}{\color{#B52F1B}\texttt{E}} \frac{\color{#2D2F91}\texttt{101001}}{\color{#B52F1B}\texttt{C}} \frac{\color{#2D2F91}\texttt{0001}}{\color{#B52F1B}\texttt{O}} \frac{\color{#2D2F91}\texttt{010}}{\color{#B52F1B}\texttt{N}} \frac{\color{#2D2F91}\texttt{100}}{\color{#B52F1B}\texttt{T}} \cdots \]

各アルファベットの Sallows の文章での出現頻度、Huffman 符号におけるコスト、Sallows の文章全体を符号化したときの全体の長さへの寄与を次の表にまとめます: \[ \small \def\arraystretch{1.2} \begin{array}{|c|c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c|} \hline \text{char} & \texttt{\color{#B52F1B}A} & \texttt{\color{#B52F1B}C} & \texttt{\color{#B52F1B}D} & \texttt{\color{#B52F1B}E} & \texttt{\color{#B52F1B}F} & \texttt{\color{#B52F1B}G} & \texttt{\color{#B52F1B}H} & \texttt{\color{#B52F1B}I} & \texttt{\color{#B52F1B}L} & \texttt{\color{#B52F1B}N} & \texttt{\color{#B52F1B}O} & \texttt{\color{#B52F1B}R} & \texttt{\color{#B52F1B}S} & \texttt{\color{#B52F1B}T} & \texttt{\color{#B52F1B}U} & \texttt{\color{#B52F1B}V} & \texttt{\color{#B52F1B}W} & \texttt{\color{#B52F1B}X} & \texttt{\color{#B52F1B}Y} & \texttt{\color{#B52F1B}Z} \\ \hline \text{freq} & 3 & 3 & 2 & 26 & 5 & 3 & 8 & 13 & 2 & 16 & 9 & 6 & 27 & 22 & 2 & 5 & 8 & 4 & 5 & 1 \\ \hdashline \text{depth} & 6 & 6 & 7 & 3 & 5 & 6 & 4 & 4 & 6 & 3 & 4 & 5 & 3 & 3 & 6 & 5 & 4 & 5 & 5 & 7 \\ \hdashline \text{total} & 18 & 18 & 14 & 78 & 25 & 18 & 32 & 52 & 12 & 48 & 36 & 30 & 81 & 66 & 12 & 25 & 32 & 20 & 25 & \hspace{0.25em}7\hspace{0.25em} \\ \hline \end{array} \]

この Huffman 符号で文章全体を符号化したときの長さは 649 ビットです。異なる Huffman 符号では同じ文字に違う符号が割り当てられ、符号の長さが違うことさえあり得ます。しかしそれでも、全ての Huffman 符号は文章全体を 649 ビットという同じ長さで符号化します。

Huffman のアルゴリズムはとても単純なので、このアルゴリズムが最適な接頭独立二進符号を生成するというのは驚きです⁶。Sallows の文章をどんな接頭独立二進符号で符号化したとしても、最低 649 ビットかかるというのです！しかし幸いにもこのアルゴリズムは再帰的なので、これまでの最適性の証明で使ってきた交換の議論を使えば証明は簡単です。まずアルゴリズムの最初の選択が正しいことを示すことから始めます。

命題 4.5 $x, y$ を最も頻度の低い二つの文字とする (いくつかあるなら適当に選ぶ)。 $x, y$ が兄弟であるような最適符号木が存在する。

証明「$x, y$ が兄弟であり、かつ他のどの葉も $x, y$ と同じ深さであるか、$x,y$ よりも浅い最適符号木が存在する」という強い命題を示す。

$T$ を最適符号木とし、深さを $d$ とする。 $T$ は全二分木 (full binary tree) だから、深さ $d$ の葉の組であって兄弟であるものが存在する (帰納法で証明せよ！) 。この葉の組が $(x, y)$ ではなく $(a, b)$ だったと仮定する。

$T$ の $x$ と $a$ を交換して得られる符号木を $T^{\prime}$ とし、$\Delta = d - \mathit{depth}_{T}(x)$ とする。この交換によって $x$ の深さは $\Delta$ 増え、$a$ の深さは $\Delta$ 減る。したがって \[ \mathit{cost}(T^{\prime}) = \mathit{cost}(T) + \Delta \cdot (f[x] - f[a]) \] が成り立つ。$x$ の頻度が一番目または二番目に小さく $a$ はそうでないという仮定から $f[x] \leq f[a]$ であり、加えて $a$ の $T$ における深さが木の深さ $d$ と等しいことから $\Delta > 0$ である。よって $\mathit{cost}(T^{\prime}) \leq \mathit{cost}(T)$ となる。一方 $T$ は最適符号木だから $\mathit{cost}(T^{\prime}) \geq \mathit{cost}(T)$ である。したがって $\mathit{cost}(T^{\prime}) = \mathit{cost}(T)$ 、すなわち $T^{\prime}$ もまた最適符号木である。

同様に $T^{\prime}$ の $y$ と $b$ を交換しても最適符号木が得られる。この最適符号木は $(x, y)$ を一番深い兄弟に持つ。 $\Box$

ここまでくれば、最適性は私たちの親愛なる友人である再帰の妖精によって保証されます！再帰的な議論は次の少し変わった全二分木の定義によって行われます: 「全二分木はただ一つの頂点からなる木であるか、そうでなければ、全二分木の任意の葉を二つの葉を子として持つ頂点と交換した木である」

定理 4.6 任意の Huffman 符号は最適な接頭独立二進符号である。

証明文章に一つか二つの文字しか含まれていない場合、定理は明らかである。以下ではそうでないと仮定する。

元の問題に対する入力の頻度を $f[1..n]$ とし、一般性を失うことなく $f[1]$ と $f[2]$ が最も頻度の低い二つの文字だと仮定する。再帰的な小問題を組み立てるために、$f[n+1] = f[1] + f[2]$ とする。先に示した命題より、文字 $1$ と文字 $2$ は $f[1..n]$ に対する最適な符号木の少なくとも一つで兄弟である。

$T^{\prime}$ を $f[3..n+1]$ に対する Huffman 符号木とする。帰納法の仮定より、$T^{\prime}$ は $f[3..n+1]$ に対する最適な符号木である。最終的な答え $T$ を得るには、$T^{\prime}$ で $n+1$ とラベルの付いた木を、文字 $1$ と文字 $2$ とラベルの付いた子を持つ頂点で置き換えればよい。こうして作った $T$ が元の頻度配列 $f[1..n]$ に対する最適符号木であることを示す。

これを示すためには、$T$ のコストを $T^{\prime}$ のコストを使って次のように書き直す。式中では $\mathit{depth}(i)$ が $i$ とラベルが付いた頂点の $T$ および $T^{\prime}$ における深さを表す。 $T$ と $T^{\prime}$ 両方に表れる頂点が同じ深さを持つことは明らかである。 \[ \small \begin{aligned} \mathit{cost}(T) & = \sum_{i=1}^{n} f[i] \cdot \mathit{depth}(i) \\ & = \sum_{i=3}^{n+1} f[i] \cdot \mathit{depth}(i) + f[1] \cdot \mathit{depth}(1) + f[2] \cdot \mathit{depth}(2) - f[n+1] \cdot \mathit{depth}(n+1) \\ & = \mathit{cost}(T^{\prime}) + (f[1] + f[2]) \cdot \mathit{depth}(T) - f[n+1] \cdot (\mathit{depth}(T) - 1) \\ & = \mathit{cost}(T^{\prime}) + f[1] + f[2] + (f[1] + f[2] - f[n+1]) \cdot (\mathit{depth}(T) - 1) \\ & = \mathit{cost}(T^{\prime}) + f[1] + f[2] \end{aligned} \]

この式は $T$ のコストの最小化が $T^{\prime}$ の最小化と同じことであること、具体的には $T^{\prime}$ で $n+1$ 番目とラベルの付いた頂点に $1$ と $2$ の頂点をつけると元の頻度対する最適符号木が手に入ることを示している。 $\Box$

効率的に Huffman 符号を構築するには、文字の頻度を優先度とした優先度付きキューを使うと上手く行きます。また出来上がった符号木を表すには、各頂点の左の子、右の子、親、を格納した三つの添え字配列を使うと便利です。最終的な符号木における葉は $1$ から $n$ までの添え字で表され、根は $2n-1$ の添え字で表されます。

Huffman のアルゴリズムの疑似コードを以下に示します。 $\textsc{BuildHuffman}$ は $O(n)$ 回の優先度付きキューの操作を行います: 正確には $\textsc{Insert}$ を $2n-1$ 回、$\textsc{ExtractMin}$ を $2n-2$ 回です。優先度付きキューを通常の二分ヒープを使って実装すれば各操作の実行時間は $O(\log n)$ なので、アルゴリズム全体の実行時間は $\pmb{O(n \log n)}$ です。

procedure $\texttt{BuildHuffman}$($f[1..n]$)

for $i \leftarrow 1$ to $n$ do

$L[i] \leftarrow 0;\ R[i] \leftarrow 0$

$\texttt{Insert}$($i, f[i]$)

for $i \leftarrow n$ to $2n - 1$ do

$x \leftarrow$$\texttt{ExtractMin}$() $\quad$ ⟨⟨頻度の低い二つの文字を取り出す⟩⟩

$y \leftarrow$$\texttt{ExtractMin}$()

$f[i] \leftarrow f[x] + f[y]$ $\quad$ ⟨⟨マージして新しい文字とする⟩⟩

$\texttt{Insert}$($i, f[i]$)

$L[i] \leftarrow x;\ P[x] \leftarrow i$ $\quad$ ⟨⟨木のポインタを更新する⟩⟩

$R[i] \leftarrow y;\ P[y] \leftarrow i$

$P[2n-1] \leftarrow 0$

return $L[1..2n-1],\ R[1..2n-1],\ P[1..2n-1]$

図 4.3

Huffman 符号の構築

最後に、構築された符号木で文章の符号化/複合化を行う単純なアルゴリズムを示します。符号化後の文章の長さを $m$ とすると、実行時間はどちらも $O(m)$ です。

procedure $\texttt{HuffmanEncode}$($A[1..k]$)

$m \leftarrow 1$

for $i \leftarrow 1$ to $k$ do

$\texttt{HuffmanEncodeOne}$($A[i]$)

return $B[1..m-1]$

procedure $\texttt{HuffmanEncodeOne}$($x$)

if $x < 2n - 1$ then

$\texttt{HuffmanEncodeOne}$($P[x]$)

if $x = L[P[x]]$ then

$B[m] \leftarrow 0$

else

$B[m] \leftarrow 1$

$m \leftarrow m + 1$

procedure $\texttt{HuffmanDecode}$($B[1..m]$)

$k \leftarrow 1$

$v \leftarrow 2n-1$

for $i \leftarrow 1$ to $m$ do

if $B[i] = 0$ then

$v \leftarrow L[v]$

else

$v \leftarrow R[v]$

if $L[v] = 0$ then

$A[k] \leftarrow v$

$k \leftarrow k + 1$

$v \leftarrow 2n - 1$

return $A[1..k-1]$

図 4.4

Huffman 符号を使った符号化と複合アルゴリズム

安定マッチング

毎年数千人の新米医師が合衆国中の病院のインターンとなります。二十世紀の最初の 50 年の間に良い医師を求める病院同士の競争は激しさを増していき、医学学校にいる生徒へのインターンシップの勧誘はどんどん早くなっていきました。時には二年生の生徒にまで締め切りの短い勧誘が来ることがあったといいます。このような状況を受けて、1940 年代に全国の医学校は生徒が 4 年生の特定の日になるまではインターンの情報を解禁しないということで合意しました。

しかしこの結果として、病院側は勧誘に対する返答の締め切りを早めるようになりました。1950 年ごろまでは病院が新米の医師を呼び付け、インターンの勧誘を行い、即時の返答を要求することも稀ではありませんでした。選択肢として三番目の病院から連絡を受けた場合、インターンは後から来るもっと良い病院からのオファーが無駄になるリスクを取ってそれを受け入れるか、それともどこにも受け入れてもらえなくなるリスクを取って拒否するかというギャンブルを迫られることになります⁷。

1950 年代の初頭になってついに National Resident Matching Program (NRMP) が設立され、インターンの割り当てに関する情報はこの機関が管理するようになりました。毎年、医師はインターンに行きたいと思っている病院をランク付けしたものを提出し、病院はインターンとして受け入れたいと思っている医師をランク付けしたものを提出します。 NRMP は提出された情報を使って病院と医師のマッチングを計算しますが、このとき次の安定性 (stability) に関する条件が満たされるようにします。

マッチングが安定でない (unstable) とは、そのマッチングではマッチしていないある医師 $\alpha$ とある病院 $B$ があって、両者をマッチさせた方が両者とも現在よりも幸せになる、つまり:

医師 $\alpha$ は病院 $A$ とマッチしているが、病院 $B$ の方がランクが高い。
病院 $B$ は医師 $\beta$ とマッチしているが、医師 $\alpha$ の方がランクが高い。

という状況が生じていることを言います。このような場合、$(\alpha, B)$ を不安定ペア (unstable pair) と言います。 NRMP の目標は不安定ペアの無い安定マッチング (stable matching) を見つけることです。

問題を単純にするために、病院の数と医師の数は等しく、全ての病院はちょうど一つのインターンを募集し、全ての医師/病院は全ての病院/医師をランク付けし、病院と医師の作るランク付けに同着は無いものとします⁸。

上手く行かない例いくつか

一目見ただけでは、安定マッチングが必ず存在するかさえ分かりません！ただ、不安定な病院と医師のマッチングが存在することは確かです。例えば Dr. Quincy, Dr. Rotwang, Dr. Shephard という三人の医師 (小文字で表す) と Arkham Asylum, Bethlem Royal Hospital, County General Hospital という三つの病院 (大文字で表す) があり、それぞれを次のようにランク付けしたとします: \[ \begin{array}{cccc} q & r & s \\ \hline A & C & A \\ C & A & B \\ B & B & C \end{array} \quad \begin{array}{cccc} A & B & C \\ \hline r & s & q \\ q & q & r \\ s & r & s \end{array} \]

このときマッチング $\lbrace Aq, Br, Cs \rbrace$ は不安定です。なぜなら Arkham は Dr.Quincy よりも Dr.Rotwang を受け入れたがっていて、 Dr. Rotwang は Bedlam よりも Arkham で働きたがっているからです。つまりこのマッチングでは $(A, r)$ が不安定ペアです。

適当なマッチングから初めて、不安定ペアを貪欲に解消していって少しずつ解に近づくというアルゴリズムを考えるかもしれません。しかし残念ながら、不安定ペアを取り除くと新しく不安定ペアができてしまうことがあります。さらに、この段階的な "改善" が無限ループを起こす場合があります。例えば先ほどの不安定なマッチング $\lbrace Aq, Br, Cs \rbrace$ から始めて次のように (矢印の上に示した) 不安定ペアを交換して解消していくと、最初のマッチングに戻ってきます⁹: \[ \lbrace Aq, Br, Cs \rbrace \overset{Ar}{\rightarrow} \lbrace Ar, Bq, Cs \rbrace \overset{Cr}{\rightarrow} \lbrace As, Bq, Cr \rbrace \overset{Cq}{\rightarrow} \lbrace As, Br, Cq \rbrace \overset{Aq}{\rightarrow} \lbrace Aq, Br, Cs \rbrace \]

あるいは、次に示す多段階の貪欲アルゴリズムを考えるかもしれません: 各反復でまずマッチしていない病院がマッチしていない中で一番ランクの高い医師を獲得し、次にマッチしていない医師がマッチしていない中で一番ランクの高い病院からの勧誘を承諾するというものです。反復ごとに最低でも一人の新しい病院と医師のペアが作られることを示すのは難しくないので、このアルゴリズムはマッチングを計算します。先ほどの例を入力すると、最初の反復で安定マッチング $\lbrace Ar, Bs, Cq \rbrace$ が得られます！しかし、次の入力を考えてみてください: \[ \begin{array}{cccc} q & r & s \\ \hline C & A & A \\ B & C & B \\ A & B & C \end{array} \quad \begin{array}{cccc} A & B & C \\ \hline q & q & s \\ s & r & r \\ r & s & q \end{array} \]

最初の反復で Dr.Shephard は Country からのオファーを受け入れ、 Fr.Quincy は (Arkham からのオファーを断って) Bedlam からのオファーを受け入れます。この結果 Dr.Rotwang と Arkham がマッチせずに残ります。よって二回目の反復でこの両者がマッチされ、マッチング $\lbrace Ar, Bq, Cs \rbrace$ が出力されます。残念ながらこのマッチングでは Arkham と Dr. Shephard がお互いを現在のマッチ相手よりも好んでいるので、このマッチングは不安定です。

Boston Pool と Gale-Shapley のアルゴリズム

1952年、NRMP はインターンの割り当てにおいて「Boston Pool (ボストンプール)」アルゴリズムを利用することを決定しました。この名前は以前に同じアルゴリズムが Boston のとある地域手形交換所で使われていたことに由来します。それから 10 年後、David Gale (デイヴィッド・ゲール) と Lloyd Shapley (ロイド・シャープレー) は Boston Pool のアルゴリズムを一般化したものを提案し、詳細な解析を行いました。その結果として、このアルゴリズムが常に安定マッチングを計算することを証明しています。このとき Gale と Shapley は大学入試の比喩を使いました。

本質的に同じアルゴリズムは 1972 年に Elliott Peranson (エリオット・ペランソン) によって医学校の入試のために開発されています。また同様のアルゴリズムは様々なマッチング市場で利用されており、例えばフランスにおける学部教員の雇用、合衆国における経済学 Ph.D. の雇用、ドイツにおける大学入試、ニューヨークとボストンにおける公立校の入試、米海軍の船員に対する宿舎割り当て、そして腎臓のマッチングプログラムに使われています。

Shapley は 2012 年に安定マッチングに関する研究でノーベル賞を受賞しました。共同受賞者は Shapley の研究を大きく拡張し、現実世界への応用を示した Albin Roth (アルヴィン・ロス) です (Gale は 2008 年に亡くなっていたので、一緒に賞を受賞することはできませんでした)。

Gale-Shapley のアルゴリズムは、最後に示した上手く行かない貪欲アルゴリズムと同じように、反復ごとに少しずつマッチングを作成していきます。各反復は二つのステージからなります:

マッチしていない病院を適当に選んで $A$ とし、$A$ からのオファーを断っていない医師の中で一番ランクが高い医師 $\alpha$ にオファーを出す。
$\alpha$ がマッチしていない場合、$\alpha$ は $A$ からのオファーを (暫定的に) 受け入れる。 $\alpha$ が既にマッチを持っていて、$\alpha$ のマッチ相手のランクが $A$ のランクより低い場合、$\alpha$ は現在のマッチを解消して $A$ からのオファーを (暫定的に) 受け入れる。そうでない場合は、$\alpha$ は $A$ からの新しいオファーを拒否する。

この処理を反復すると全ての医師はランク付けに従って一番良い病院からのオファーを受けることになります¹⁰。このアルゴリズムを簡単に言うと、病院は貪欲にオファーを出し、医師はオファーを貪欲に受け入れるということです。双方が貪欲になるこの戦術が上手く行く鍵は、医師がより良いオファーを受け取った場合に現在持っているオファーを断れる点です。

例えば、四人の医師 (Dr. Quincy, Dr. Rotwang, Dr. Shephard, and Dr. Tam) と四つの病院 (Arkham Asylum, Bethlem Royal Hospital, County General Hospital, and The Dharma Initiative) が双方を次のようにランク付けしたとします: \[ \begin{array}{cccc} q & r & s & t \\ \hline A & A & B & D \\ B & D & A & B \\ C & C & C & C \\ D & B & D & A \end{array} \quad \begin{array}{cccc} A & B & C & D \\ \hline t & r & t & s \\ s & t & r & r \\ r & q & s & q \\ q & s & q & t \\ \end{array} \] この入力に対する Gale-Shapley のアルゴリズムの実行例は次のようになります:

Arkham が Dr. Tam にオファーを出す。Dr. Tam はこのオファーを受け入れる。
Bedlam が Dr. Rotwang にオファーを出す。Dr. Rotwang はこのオファーを受け入れる。
County が Dr. Tam にオファーを出す。 Dr. Tam は Arkham からのオファーを断って、このオファーを受け入れる。
Dharma が Dr. Shephard にオファーを出す。Dr. Shephard はこのオファーを受け入れる (ここから先マッチしていない医師と病院の組が一つだけになるので、処理に恣意性がなくなる)。
Arkham が Dr. Shephard にオファーを出す。Dr. Shephard は Dharma からのオファーを断って、このオファーを受け入れる。
Dharma が Dr. Rotwang にオファーを出す。Dr. Rotwang は Bedlam からのオファーを断って、このオファーを受け入れる。
Bedlam が Dr. Tam にオファーを出す。Dr. Tam は County からのオファーを断って、このオファーを受け入れる。
County が Dr. Rotwang にオファーを出す。Dr. Rotwang はこのオファーを断る。
County が Dr. Shephard にオファーを出す。Dr. Shephard はこのオファーを断る。
County が Dr. Quincy にオファーを出す。Dr. Quincy はこのオファーを受け入れる。

10 回目の反復が終わると暫定的な全てのオファーが受け入れられ、アルゴリズムはマッチング $\lbrace As, Bt, Cq, Dr \rbrace$ を出力します。このマッチングが安定であることは総当たりで確認できます (自分でやってみるべきです)。ここで注目してほしいのが、ランクが一位の病院に雇われた医師は一人もおらず、ランクが一位の医師を雇った病院も一つもない点です。さらに Country にいたっては三位にランク付けした病院に雇われています。しかしそれでもこのマッチングは安定です。またこの入力に対する安定マッチングはこれだけではなく、例えば $\lbrace Ar, Bs, Cq, Dt \rbrace$ も安定です。

実行時間

このアルゴリズムの実行中に出されるオファーの数を数えるのは比較的簡単です (なので最初にやってしまいます)。全ての病院は全ての医師に対して最大 1 回のオファーを出します。よって全体で $n^{2}$ 個のオファーが出されます。

オファーの数ではなくて実際の実行時間を解析するには、アルゴリズムをさらに細かく規定していく必要があります。ランク表はどのように与えられる？ある病院がマッチしていないことをどうやって判断する？マッチしていない病院を見つけるにはどうすれば？暫定的なマッチングをどうやって保存すれば良い？医師にとって今のマッチと新しいオファーのどちらがいいかをどうやって判断する？そして最も基本的なこととして: 医師と病院をどう表す？

医師と病院を表す一つの方法は、医師と病院を $1$ から $n$ の整数を使って表し、ランク表を二つの配列 $\mathit{Dpref}[1..n, 1..n]$ と $\mathit{Hpref}[1..n, 1..n]$ を使って表すというものです。ここで $\mathit{Dpref}[i,r]$ は $i$ 番目の医師が $r$ 番目にランク付けする病院を表し、$\mathit{Hpref}[j,r]$ は $j$ 番目の病院が $r$ 番目にランク付けする医師を表します。入力がこの形だとすれば、 Boston Pool のアルゴリズムは各オファーの処理を定数時間で行うことができ、それ以外に前処理が少しあるだけなので、全体の実行時間は $\pmb{O(n^{2})}$ となります。残りの詳細は簡単な練習問題として残しておきます。

もう少し難しい練習問題としては、アルゴリズムが終了するまでに $\Omega(n^{2})$ 回のオファーが必ず生じるような入力 (とオファーを出す病院の順番) を作る問題があります。この問題には答えがあることから、最悪ケースで $O(n^{2})$ という実行時間の上界は厳密です。

正しさ

いったいどうしてこのアルゴリズムは正しいのでしょうか？このアルゴリズムが安定マッチングを計算すること、さらに言えばそもそもアルゴリズムが停止して、出力が完全なマッチングであることだって、証明無しには分かりません。

医師が一度でもオファーを受け取ると、それ以降その医師は暫定的なマッチを持ち続けます。逆にマッチされていない医師がいる場合にはそれまでにどの病院もその医師にオファーを行っておらず、全ての医師にオファーを出した病院がないことが分かります。したがってこのアルゴリズムは (最大で $n^{2}$ ラウンドの後に) 停止し、そのとき全ての医師と病院がマッチされることが分かります。つまり、Gale-Shapley のアルゴリズムは医師と病院の間の完全なマッチングを計算します (ヒュー！)。後はこのマッチングが安定であることを示すだけです。

このアルゴリズムが最終的に医師 $\alpha$ と病院 $A$ をマッチさせた場合に、$\alpha$ が $A$ よりも $B$ を高くランク付けしていたとします。全ての医師は受け取ったオファーの中で一番いいものを選ぶことから、$\alpha$ は $A$ よりも良いオファーを受け取っていません。特に、$\alpha$ は $B$ からのオファーを受け取っていません。一方 $B$ は最終的なマッチ相手 $\beta$ を選ぶまでにそれよりランクの高い医師全員にオファーを出していることから、$B$ にとって $\alpha$ は $\beta$ よりもランクが下です。したがって $(\alpha, B)$ は不安定ペアではありません。以上より、アルゴリズムが出力するマッチングに不安定ペアはありません: つまり、安定です！

最適性！

驚くべきことに、Gale-Shapley アルゴリズムの正しさの証明は各反復でオファーを出す病院の選択に依存していません。実は、各反復でオファーを出す病院をどのように選んだとしても、アルゴリズムは必ず同じマッチングを計算します！

病院 $A$ と医師 $\alpha$ をマッチさせる安定マッチングが存在する場合、$\alpha$ は $A$ に対して適合 (feasible) であると言うことにします。このとき、次の命題が成り立ちます。

命題 4.7 Gale-Shapley のアルゴリズムにおいて、病院 $A$ のオファーは $A$ に対して不適合な医師によってのみ断られる。

証明反復の回数に関する帰納法で示す。アルゴリズムのある反復で、医師 $\alpha$ が病院 $A$ からのオファーを断って病院 $B$ のオファーを受け入れたとする。オファーを断ったことから、$\alpha$ は $A$ よりも $B$ を高くランク付けしている。また $B$ のランク付けで $\alpha$ よりも高い順位にある医師は全てこれまでの反復で $B$ からのオファーを断っており、帰納法の仮定から、そのような医師は全員 $B$ に対して不適合である。

$\alpha$ と $A$ をマッチさせる (同じ医師と病院の間の) 任意のマッチングを考える。 $\alpha$ が $A$ よりも $B$ を高くランク付けしていることは見た。もし $B$ が今のマッチ相手より $\alpha$ を高くランク付けするなら、このマッチングは不安定である。そうでなくて $B$ が今のマッチ相手よりも $\alpha$ を低くランク付けするなら、(前の段落の議論より) その相手は $B$ に対して不適合であり、マッチングは不安定となる。したがって $\alpha$ と $A$ をマッチさせるような安定マッチングは存在せず、$\alpha$ は $A$ に対して不適合である。 $\Box$

さらに、$\pmb{\mathit{best}(A)}$ で病院 $A$ に対して適合な医師の中で $A$ のランク付けが最上位の医師を表すことにします。命題 4.7 から、任意の病院のランク付けにおいて最終的なマッチ相手よりもランクが上にある医師はその病院に対して不適合であることが言えるので、次の命題は明らかです。

系 4.8 任意の病院 $A$ に対して、Gale-Shapley のアルゴリズムは $A$ と $\mathit{best}(A)$ をマッチさせる。

言い換えると、Gale-Shapley のアルゴリズムが計算するのは安定マッチングの中でも病院から見て最良のものであるということです。さらに、このマッチングは医師から見ると最悪のものであることが示せます！ $\pmb{\mathit{worst}(\alpha)}$ で医師 $\alpha$ に対して適合な病院の中でランク付けが最下位の病院を表すことにします。

系 4.9 任意の医師 $\alpha$ に対して、Gale-Shapley のアルゴリズムは $\alpha$ と $\mathit{worst}(\alpha)$ をマッチさせる。

証明 Gale-Shapley のアルゴリズムが医師 $\alpha$ を病院 $A$ にマッチさせたとする。 $A = \mathit{worst}(\alpha)$ を示せばよい。 $A$ が $\alpha$ ではない別の医師 $\beta$ とマッチしている任意の安定マッチングを考える。一つ前の系から、$A$ は $\beta$ よりも $\mathit{best}(A) = \alpha$ を高くランク付けする。マッチングが安定なことから、$\alpha$ は $A$ よりも現在のマッチ相手を高くランク付けしていなければならない。この議論は任意の安定マッチングに適用できるので、$\alpha$ は $A$ 以外の全ての適合な病院を $A$ よりも高くランク付けする。すなわち $A = \mathit{worst}(\alpha)$ である。 $\Box$

Lester Dubins (レスター・デュビンズ) と David Freedman (デイビット・フリードマン) によって 1981 年に示されたこの二つの系からの帰結によると、医師は自分のランク付けを偽ることでマッチング結果を改善できますが、病院にはできません (ただし複数の病院が結託すればその病院の一部のマッチングを改善できます)。このこともあって、National Residency Matching Program は今までの説明とは逆の、新米医師からランク付けに沿ってオファーを出して、病院がそれを受け入れるというアルゴリズムを 1998 年から採用しています。この方法では医師にとって最良、病院にとって最悪の安定マッチングとなります。実際のデータでは、この反転で生じるマッチングの変化は 1 % 以下です。また私の知っている限り、このアルゴリズムの変更で生じる患者への影響は誰も手を付けていない問題です。

練習問題

読者への注意: 貪欲アルゴリズムを使って解けない問題が混じっています！ また貪欲アルゴリズムを説明、解析するときには正しさの証明を必ず付けてください。証明は通常交換の議論の形をしているはずです。普通の問題では正しさの証明を要求しない (私の担当しているような) 講義において、この証明は特に重要となります。

講義のスケジューリング問題に対する $\textsc{GreedySchedule}$ アルゴリズムは、この問題に対する唯一の貪欲アルゴリズムであるというわけではありません。このアルゴリズムとは異なる貪欲な戦術をいくつか次に示します。それぞれについて、その戦術が常に最適なスケジュールを生成するならそのことを証明し、そうでないなら最適なスケジュールが出力されない入力のうちできる限り小さいものを示してください。アルゴリズムの途中で同着の講義が生じた場合にはランダムに選択する (あなたが選択を管理することはできない) と仮定してください。 [ヒント: 正しいアルゴリズムは三つだけです。]
1. 最も遅く終わる講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
2. 最も早く始まる講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
3. 最も遅く始まる講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
4. 最も短い講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
5. 衝突する講義の数が一番少ない講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
6. 考えている講義に衝突が無いなら、それらを全て選んで終了。そうでないなら、一番長い講義を除去して再帰的に処理する。
7. 考えている講義に衝突が無いなら、それらを全て選んで終了。そうでないなら、衝突する講義が最も多い講義 $x$ を除去して再帰的に処理する。
8. 一番早く始まる講義を $x$ 、二番目に早く始まる講義を $y$ とする。
  - $x$ と $y$ が衝突しないなら、$x$ を選んで $x$ 以外の講義について再帰的に処理する。
  - $x$ が $y$ を完全に含むなら、$x$ を除去して再帰的に処理する。
  - それ以外の場合は、$y$ を除去して再帰的に処理する。
9. ある講義 $x$ の時間が他の講義の時間を完全に含むなら、$x$ を除去して再帰的に処理する。そのような講義が無いなら、最も遅く終了する講義 $y$ を選び、$y$ と衝突する講義を取り除き、再帰的に処理する。
重み付きの講義スケジューリング問題を考えます。各講義はそれぞれ単位時間 (講義の時間とは無関係) を持っており、衝突しない講義の集合で単位時間を最大化するものの計算が目標です。入力は講義の開始時間、終了時間、単位時間を表す三つの配列です。
1. この章の最初に説明した貪欲アルゴリズム ――一番早く終わるものを選んで再帰的に処理する―― が常に最適なスケジュールを返すわけではないことを示してください。
2. 練習問題 4.1 で説明したアルゴリズムはどれも常に最適なスケジュールを返すわけではないことを示してください。 [ヒント: 練習問題 4.1 を先に解いてください。この問題で上手く行かないアルゴリズムはここでも上手く行きません。]
3. 常に最適なスケジュールを計算するアルゴリズムを説明、解析してください。 [ヒント: 答えは貪欲アルゴリズムではありません。]
数直線上の $n$ 個の区間の集合を $X$ とします。 $X$ の部分集合 $Y$ が $X$ を覆う (cover する) とは、$Y$ に含まれる区間の和集合が $X$ に含まれる区間の和集合と等しいことを言います。$X$ を覆う $X$ の部分集合で最小のものを計算する効率の良いアルゴリズムを説明、解析してください。入力は $X$ に含まれる区間の始点と終点を表す配列 $L[1..n]$ と $R[1..n]$ とします。もし貪欲アルゴリズムを使うなら、その正しさを必ず証明してください。

区間の集合とそれを覆う大きさ $7$ の部分集合 (色の付いている区間)
数直線上の $n$ 個の区間の集合を $X$ とします。数直線上の点の集合 $P$ が $X$ を貫く (stab する) とは、 $X$ に含まれる全ての区間が少なくとも一つの $P$ の点を含むことを言います。 $X$ を貫く最小の点集合を求める効率の良いアルゴリズムを説明、解析してください。入力は $X$ に含まれる区間の始点と終点を表す配列 $L[1..n]$ と $R[1..n]$ とします。もし貪欲アルゴリズムを使うなら、いつも通りその正しさを証明してください。

四つの点 (垂直な線分) で貫かれる区間の集合
数直線上の $n$ 個の区間の集合を $X$ とします。 $X$ の真の彩色 (proper coloring) とは、$X$ に含まれる全ての区間に対する色の割り当てであって重なり合うどの区間も同じ色で塗られないものを言います。 $X$ の真の彩色の持つ最小の色数を計算する効率の良いアルゴリズムを説明、解析してください。入力は $X$ に含まれる区間の始点と終点を表す配列 $L[1..n]$ と $R[1..n]$ とします。もし貪欲アルゴリズムを使うなら、いつも通りその正しさを証明してください。

区間の集合に対する五つの色を使った正しい彩色
1. 任意の整数 $n$ に対して、 Huffman 符号木の高さが $n-1$ となるような頻度配列 $f[1..n]$ であって最大の頻度が最小のものを求めてください。
2. 符号化前の文章の長さ $N$ がアルファベットのサイズ $n$ の多項式で抑えられているとします。この文章の頻度配列 $f[1..n]$ に対する Huffman 符号木の高さが $O(\log n)$ であることを示してください。
❤ 頻度配列 $f[1..n]$ が次の二つの条件を満たすとき、$\pmb{\alpha}$-heavy であると言います。
- 任意の $i > 1$ に対して $f[1] > f[i]$; つまり、記号 $1$ が狭義に最も頻度の高い記号である。
- $f[1] \geq \alpha \sum_{i=1}^{n} f[i]$; つまり、メッセージに含まれる全ての記号のうち、記号 $1$ の割合が $\alpha$ よりも大きい。
任意の $\alpha$-heavy な頻度配列に対する全ての Huffman 符号において文字 $1$ が一ビットで表されるような実数 $\alpha$ の最小値を求めてください。 [ヒント: まず $1 / 3 \leq \alpha \leq 1 / 2$ を示してください。]
与えられた頻度配列 $f[1..n]$ に対する最適な線形独立三進符号を求めるアルゴリズムを説明、解析してください。全ての $n$ に対して正しいことを示すのを忘れないでください。
先述したGale-Shapley のアルゴリズムの、最悪実行時間が $O(n^{2})$ である実装を詳細に説明してください。
1. Gale-Shapley のアルゴリズムが停止するまでに $\Omega(n^{2})$ 回のオファーを出すことがあり得ることを証明してください (アルゴリズムに対する実際の入力とそれに対する $\Omega(n^{2})$ 個の正しいオファーの列を示してください)。
2. 任意の $n$ に対して、Gale-Shapley のアルゴリズムを実行したときに各反復でどんなオファーが出されたとしても停止するまでに $\Omega(n^{2})$ 回の反復を要するような、$n$ 人の医師と $n$ 個の病院のランク付けを示してください。 [ヒント: (b) が示せれば自動的に (a) も示せます。]
与えられた医師と病院のランク付けに対する安定マッチングが唯一であるかどうかを判定する効率の良いアルゴリズムを説明、解析してください。
次の一般化した安定マッチング問題を考えます: 医師と病院は全ての病院/医師をランク付けせず、医師と病院がマッチするのはお互いがお互いをランク付けしているときだけとします。この条件では、マッチングが不安定となる状況が三つ加わります:
- マッチ相手がいる病院が、現在のマッチ相手よりもマッチせずに残っている医師を高くランク付けしている。
- マッチ相手がいる医師が、現在のマッチ相手よりもマッチせずに残っている病院を高くランク付けしている。
- マッチしていない医師とマッチしていない病院がお互いのランク付けに現れる。
この条件における安定マッチングでは、ランク付けが空でないにもかかららずマッチしていない医師や病院があっても構いません。例えば全ての医師が Harvard だけを一位にランク付けし、全ての病院が Dr. House だけを受け入れるインターンとしてランク付けした場合、Harvard と Dr. House だけがマッチされます。

この一般化された問題に対する安定マッチングを計算する効率の良いアルゴリズムを説明、解析してください。 [ヒント: 全ての医師と病院が互いをランク付けしているような小さいインスタンスに帰着させ、Gale-Shapley のアルゴリズムを使ってください。]
スカンジナビアの家具会社 Fürni は $n$ 個の同じ荷物をデラウェア州ウィルミントン内の $n$ 箇所の異なる住所に届けるために、$n$ 人のドライバーを雇いました。各ドライバーはウィルミントン内の $n$ 箇所の住所を回るこだわりの配送ルートを持っており、配送のときには必ずそのルートに従うとします。

何も条件が無ければ $n$ 人のドライバーが $n$ 個の住所のうちどこに荷物を届けても問題は無いのですが、厄介なことが起こりました。ドライバーの一人が全ての Johannshamn のソファ (Strinne グリーンストライプパターン入り) に近接センサーと爆弾を仕掛けたのです。二つのソファが同じ時間に同じ場所にあると、両方のソファは爆発し、配送トラックと建物を吹き飛ばしてしまいます。爆発が起こるのは二人のドライバーが同じ住所に荷物を届けた場合、あるいはあるドライバーがソファを届けたあとに他のドライバーがソファを持ったままその住所を訪れた場合です。

爆発が起きないようにドライバーに届け先住所を割り当てるのが Fürni の配送管理人としてのあなたの仕事です。 $n$ 個の住所が荷物を受け取り、かつ爆発が起きないようなドライバーの住所への割り当てを計算するアルゴリズムを説明してください。

例えば、 Jack のルートは 6 pm に 537 Paper Street 、8 pm に 1888 Franklin Street に訪れるものであり、 Marla のルートは 7 pm に 537 Paper Street 、 9 pm に 1888 Franklin Street を訪れるものだとします。このとき Jack は 1888 Franklin に、 Marla は 537 Paper に配送させるのが正解の割り当てとなります。そうでない割り当てでは 8 pm に 1888 Franklin で爆発が起きてしまいます (Cue the Pixies)。 [ヒント: Jack と Marla はある意味で不安定です。]
あなたは小さな商店の店主です。あなたの住んでいる国には $n$ 種類のコインがあり、それぞれの価値は $1 = c[1] < c[2] < \cdots < c[n]$ だとします (例えば合衆国では $n=6$ で $c = [1,5,10,25,40,100]$ です)。王室大蔵省で働く公務員たちが丹精込めて硬貨に刻んだ皆から愛される慈愛に満ちた元首 El Generalissimo の肖像をすり減らしてしまわないように、店員がお釣りを渡すときにはなるべく少ない枚数の硬貨を使わなければならないという法令が制定されています。
1. 合衆国では貪欲アルゴリズムを使うと必ず最小の数の硬貨を渡すことができます。つまり、お釣りの額を超えない最大の硬貨を渡し、残りの額について再帰的に同じことをするという方法です。El Generalissimo はこの資本主義的な貪欲さを気に入りませんでした。この貪欲アルゴリズムが最小の硬貨の集合を計算するのに失敗するようなコインの価値の集合を示してください。
2. El Generalissimo は決断を下し、硬貨の単位を整数の連続するべき $b^{0},$ $b^{1},$ $b^{2},$ $\ldots,$ $b^{k}$ $(b \geq 2)$ にするとしました。この通貨制度だと El Generalissimo が嫌う貪欲アルゴリズムを使って最適なお釣りを計算できてしまうことを示してください。
3. お釣りの額 $T$ とソートされた通貨の単位 $c[1..n]$ が与えられたときに、合計が $T$ となる最小の硬貨の集合を求める効率の良いアルゴリズムを説明、解析してください。 $c[1] = 1$ であってどんな $T$ に対してもちょうどお釣りを渡せるとします。
正でもゼロでも負でもありうる整数の配列 $A[1..n]$ が与えられたとします。 $A$ の連続する部分配列 $A[i..j]$ が正の区間 (positive interval) であるとは、その和がゼロより大きいことを言います。 $A$ に含まれる全ての正の整数を覆うような正の区間の集合の大きさの最小値を求めるアルゴリズムを説明、解析してください。例えば、以下の配列が与えられたときのアルゴリズムの出力は $3$ です。また入力配列が全て負だった場合の出力は $0$ です。
次の処理を考えます。最初 $x=1$ であり、各ステップで行えるのは $x$ を $1$ 増やす increment と二倍する doubling のどちらかです。目標は整数 $n$ を作ることです。例えば、$10$ は次の 4 ステップで作ることができます: \[ 1 \overset{+1}{\longrightarrow} 2 \overset{\times 2}{\longrightarrow} 4 \overset{+1}{\longrightarrow} 5 \overset{\times 2}{\longrightarrow} 10 \] $n$ を $n-1$ 回の increment で作ることができるのは明らかですが、ほとんどの $n$ についてもっと効率的な作り方があります。与えられた整数 $n$ を作るための最小ステップ数を計算するアルゴリズムを説明、解析してください。
$n$ 人のスキーヤーの背の高さが配列 $P[1..n]$ で表され、$n$ 個のスキー板の長さが配列 $S[1..n]$ で表されるとします。スキー板とスキーヤーの高さの差の平均値が最小になるようにスキー板をスキーヤーに割り当てるアルゴリズムを説明、解析してください。アルゴリズムが計算するのは置換 $\sigma$ であって次の値を最小にするものです: \[ \frac{1}{n} \sum_{i=1}^{n} |P[i] - S[\sigma[i]]| \]
Alice はパーティを開くことになり、誰を招待しようか考えています。彼女には招待できる知り合いが $n$ 人いて、そのうち誰と誰がお互いに知り合いであるかを彼女は知っています。 Alice は次の制約の下でなるべく多くの人を招待することにしました:
- どの招待客も他の招待客の中に少なくとも 5 人の知り合いがいる。
- どの招待客も他の招待客の中に少なくとも 5 人の知り合いでない人がいる。
Alice が招待できる最大の人数を計算するアルゴリズムを説明、解析してください。アルゴリズムの入力は $n$ 人の名前と誰と誰が知り合いかを表す名前の組の配列です。
二つの正の整数の配列 $R[1..n]$ と $C[1..n]$ が与えられたとします。要素が $0$ または $1$ である $n \times n$ の行列が $R$ と $C$ の組と適合 (agree) するとは、全ての添え字 $i$ について $i$ 行目が $R[i]$ 個の $1$ を含み、$i$ 列目が $C[i]$ 個の $1$ を含むことを言います。$R$ と $C$ が与えられたときに、適合する行列を構築するか、適合する行列が存在しないならばそのことを正しく報告するアルゴリズムを説明、解析してください。
あなたはブリトーをサンフランシスコからニューヨークまで配達する仕事を Elon Musk から受託しました。あなたはブリトー配達車両を運転して最近 Elon が建設した大陸横断ブリトー配達地下トンネル¹¹を走ることになります。このトンネルは二つの都市を直線で結んでいます。

ブリトー配達車両には使い捨てのバッテリーがついており、100 マイル走るごとに取り換えなければなりません。燃料は実質無料なのですが、バッテリー自体が高価で壊れやすいために、バッテリーの交換作業を行えるのは大陸横断ブリトー配達地下トンネル車両バッテリー交換連合の正規職員¹²だけです。そのためバッテリーの残量がまだあったとしても、新しいバッテリーに交換すると料金が満額かかります。加えてあなたの車両はとても小さいので、予備のバッテリーを載せておくことができません。

トンネル内にはいくつか燃料補給所があり、場所によってバッテリーの交換にかかる料金が異なります。旅を始めるに先立って、あなたはトンネル内の全ての燃料補給所とそこでのバッテリー交換料金をリストにした Wikipedia ページを印刷しておきました。どこで燃料を補給するかをどうやって決めればよいでしょうか？

きちんと言うと、こうなります: 二つの配列 $D[1..n]$ と $C[1..n]$ が与えられ、$D[i]$ がトンネルの入口から $i$ 番目の燃料補給所までの距離を表し、$C[i]$ が $i$ 番目の燃料補給所でバッテリーを交換したときにかかる料金を表しているとします。あなたの旅は最初の燃料補給所から始まって最後の燃料補給所で終わり (つまり $D[1]=0$ で、$D[n]$ が旅の総距離を表し)、最初車両には燃料が入っていない (一番目の燃料補給所には必ず停まる) とします。
1. 旅を完了するために停車すべき燃料補給所の数の最小値を求める貪欲アルゴリズムを説明、解析してください。アルゴリズムが正しいことの証明を忘れないでください。
2. 本当に最小化したいのは停車する燃料補給所の数ではなく全体のコストです。(a) の貪欲アルゴリズムが常に最適な解を出力するわけではないことを示してください。
3. 旅の全体コストを最小化する場合に、停車すべき燃料補給所を計算する効率の良いアルゴリズムを説明してください。
あなたは $n$ 冊の本を保管する図書館に雇われました。本は索引システムに基づいて一列に並んでおり、この順番を変えることはできません: つまり、全ての棚は並んだ本の連続する一区間だけを保存できます。二つの配列 $H[1..n]$ と $T[1..n]$ が与えられ、$H[i]$ と $T[i]$ がそれぞれ $i$ 個目の本の高さと厚さを表しているとします。図書館にある全ての棚は同じ幅 $L$ を持ち、棚に入っている本の厚さの合計は $L$ を超えてはいけません。
1. 全ての本の高さが $h$ で、棚の高さは $h$ よりも大きいとします。このときどの本も棚に並べられます。最小限の棚を使って全ての本を棚に入れる貪欲アルゴリズムを説明、解析してください。 [ヒント: アルゴリズムは明らかです。でもなぜそれが正しいのでしょうか？]
2. いい準備運動でしたね。さぁ本物の問題を考えましょう。現実の図書館にある棚は異なる高さを持ちます。ただしその高さは調整でき、棚に収められている本の高さの最大値になるまで棚を低くできます (空の棚の高さを 0 にすることもできます)。棚の高さの合計が最小になるように本を棚に収めるのがあなたの仕事です。(a) の貪欲アルゴリズムが常に最適な解を出力するわけではないことを示してください。
3. (b) で説明された棚に対する最良の本の収め方を見つけるアルゴリズムを説明、解析してください。
丸括弧 $\color{green}{(}$ と $\color{#B52F1B}{)}$ からなる文字列 $w$ のバランスが取れているとは、次の条件のどれかを満たすことを言います:
- $w$ は空文字列である。
- あるバランスの取れた文字列 $x$ を使って $w = {\color{green}(} x \color{#B52F1B}{)}$ と表せる。
- あるバランスの取れた文字列 $x,y$ を使って $w = xy$ と表せる。
例えば文字列 \[ w = {\color{green}{(}}{\color{green}{(}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}} \] はバランスが取れています。なぜなら次のように $x, y$ を定義すると $w = xy$ であり、 $x$ と $y$ はバランスが取れているからです。 \[ x = {\color{green}{(}}{\color{green}{(}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}},\quad y = {\color{green}{(}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}} \]
1. 丸括弧からなる文字列が与えられたときに、その文字列のバランスが取れているかを判定するアルゴリズムを説明、解析してください。
2. 丸括弧からなる文字列が与えられたときに、その文字列に含まれるバランスの取れた部分列で最長のものの長さを計算する貪欲アルゴリズムを説明、解析してください。いつものように、正しさの証明を忘れないでください。
両方の問題について入力は $w[1..n]$ であり、$w[i] = \color{green}{(}$ または $w[i] = \color{#B52F1B}{)}$ だとします。両方のアルゴリズムの実行時間は $O(n)$ になるはずです。
ある日、ジムの壁を登るのに飽きた Alex はクライマーの友達を大勢誘って屋外の壁を登りに行きました。彼らが訪れたクライミングエリアはとても横にとても長い岩で、あまり高くはありませんでした。岩には手足を掛ける場所 (ホールド) がたくさんありましたが、それを見た Alex は友達と話し合って、"許されている" 動きを設定しました。次のホールドに移動するときには、このルールに従わなければなりません。

ホールドと許されている動きは $n$ 頂点の根付き木 $T$ で表され、頂点がホールドに、辺が許されているホールド間の動きを表します。岩を上る道は上に行くほど小さくなり、最終的にホールド一つになります。このホールドが $T$ の根に対応します。

Alex とその友達 (みな優秀なクライマーです) はなるべく多い人数で岩を同時に上るというゲームをすることになりました。ただしクライマーはちょうど $k$ 回だけ岩を上に向かって登らないといけません。つまり、クライマーは $T$ の中で根に向かって長さ $k$ の道を描きます。加えて、一つのホールドを使えるのは一人のクライマーだけです。つまりクライマーの軌跡が交差してはいけません。
1. このゲームをプレイできる最大人数を計算する貪欲アルゴリズムを説明、解析してください。アルゴリズムの入力は根付き木 $T$ と整数 $k$ であり、出力は $T$ の根に向かう長さ $k$ の互いに重ならない $T$ の路からなる集合の最大の大きさです。 $T$ が二分木だと仮定しないでください。次の例では $k=3$ であり、アルゴリズムの出力は整数 $8$ です。
  
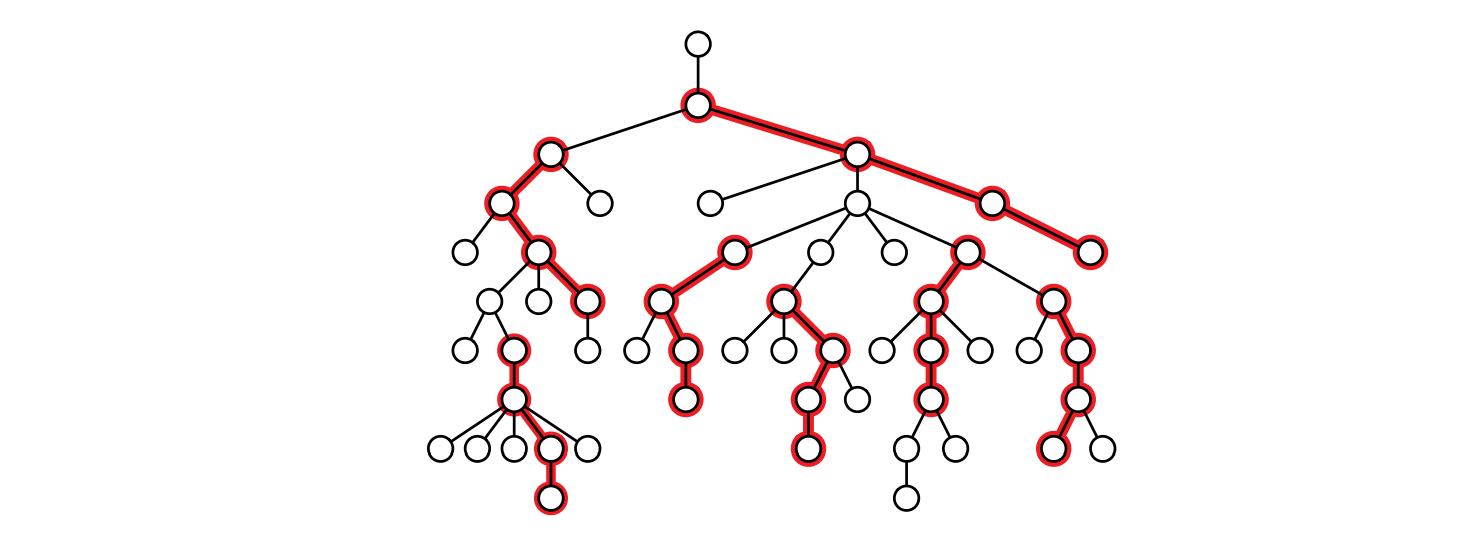  $長さが $k=3$ である重ならない 7 つの道 (これはこの木で条件を満たす最大の道の集合ではない)$
  
  図 4.6
  
  長さが $k=3$ である重ならない 7 つの道 (これはこの木で条件を満たす最大の道の集合ではない)
2. $T$ の頂点に報酬が付いているとします。この問題の目標は道の集合の大きさではなく道の集合に含まれる頂点の報酬の和を最大化することです。(a) の貪欲なアルゴリズムが常に最適な報酬を返すわけではないことを示してください。
3. (b) で説明した報酬の最大値を計算する効率の良いアルゴリズムを説明してください。
おめでとうございます！あなたは Camelot を征服しました！腐敗しきった世襲君主制は無政府組合主義のコミューンにとって代わり、市民は順番に "今週の行政官" となり、重要な決断は隔週の特別な会議で行われ、純粋に内政に関するものは過半数の賛成で、そうでない重要なものは三分の二の賛成をもって...

この征服を締めくくる象徴的な行為として、あなたは円卓 (驚くことに本当に丸い机でした) をピザのように楔形に切って、戦利品として Camelot の市民に配ることにしました。あなたは全ての市民に対して円卓のどの角度が欲しいかを聞いて回り、市民の要求を二つの角度としてまとめました。例えば Sir Robin the Brave は $17.23^{\circ}$ から $42^{\circ}$ を、 Sir Lancelot the Pure は $359^{\circ}$ から $1^{\circ}$ (の二度)を、などです。市民は要求とちょうど同じ形を受け取らない限り満足しませんが、市民の要求は重なっているので全員を満足させるのは不可能です。政治へようこそ。

満足させることができる市民の数の最大値を計算するアルゴリズムを説明、解析してください。角度が整数だと仮定しないでください。 [ヒント: アルゴリズムの出力はテーブルを回転させても変わらないはずです。]
あなたは巨大な風船に取り囲まれていて、手には真新しい Acme 印の Zap-O-Matic™ を握っています。 Zap-O-Matic™ を撃つと直進する高エネルギーレーザービームが放たれ、進路上にある風船が全て割れます。現在位置から移動することなく Zap-O-Matic™ を使って全ての風船を割るのがあなたの目標です。ただしこの銃は一発撃つのに小国が一年で消費するのと同じぐらいの電力を必要とするので、なるべく少ない銃撃で全ての風船を割らなくてはなりません。

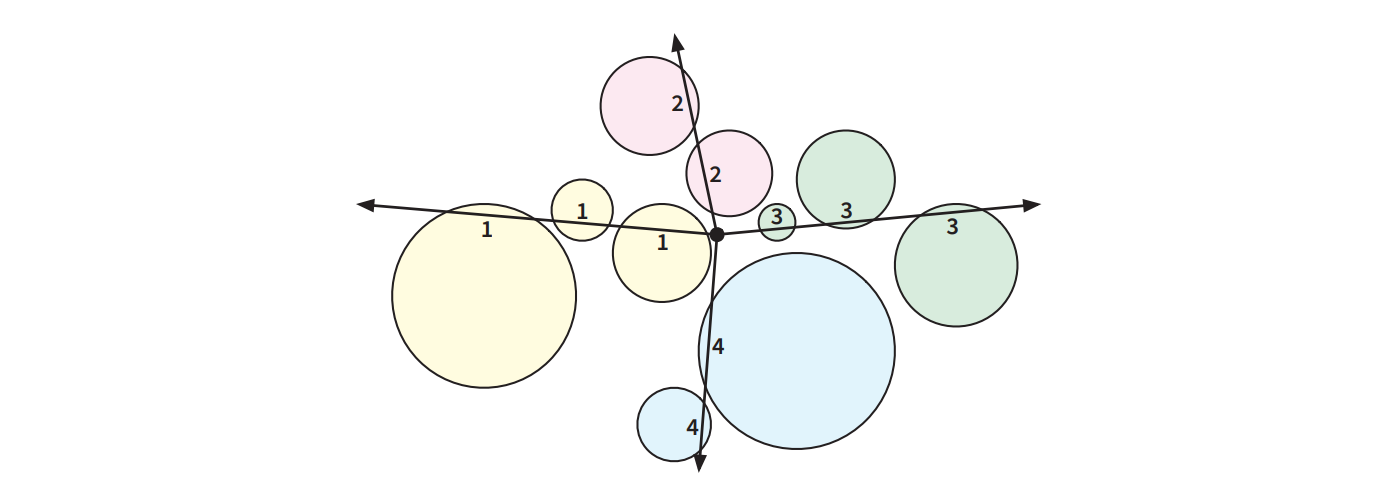図 4.7

Zap-O-Matic™ の四回の銃撃で割られる 9 個の風船

この最小 zap 問題は次のように定義できます: 「平面上の $n$ 個の円の集合 $C$ が与えられ、円が中心座標 $(x, y)$ と半径で表されるときに、原点を始点とするレイ (半直線) の集合であって全ての円がどれかと交わるものの大きさの最小値を求めよ」この問題に対する効率の良いアルゴリズムを見つけるのがこの練習問題の目標です。
1. どの風船とも交差しないレイを放つことができるとします。この最小 zap 問題の特殊ケースに対する貪欲アルゴリズムを説明、解析してください。 [ヒント: 練習問題 4.2]
2. 最適解との差が $1$ 以内であるような答えを出力する貪欲アルゴリズムを説明、解析してください。つまり、最適の場合 $m$ 個のレイで全ての風船を割ることができるときに、出力が $m$ または $m+1$ となる貪欲アルゴリズムを答えてください (もちろんこの事実を証明してください)。
3. 最小 zap 問題を $O(n^{2})$ 時間で解くアルゴリズムを説明してください。
4. ❤ 最小 zap 問題を $O(n \log n)$ 時間で解くアルゴリズムを説明してください。
任意の円 $c$ と交わるレイの角度の範囲を $O(1)$ で計算できるサブルーチンが利用可能であるとしてください。このサブルーチンを実際に書くのは難しくありませんが、これを実際に書くことがこの問題の狙いではありません。

磁気テープなんて何十年も前にお役御免になっているだろうと言いかけた人は、近くのスーパーコンピューター施設を見学に行ってテープロボットを見てくることをお勧めします。そのような施設が近くに無いなら、代わりに図書館の本棚に本を並べる処理を想像してもいいでしょう。ええ、あの木の死体とインクからできているレンガみたいな形をした奇妙な物体です。^[return]
ただしそれでも、自分で詳細を詰めてみるべきです。動的計画法を使えば異なる "良い" 基準に沿った "最良" スケジュールを見つけることができますが、貪欲アルゴリズムが見つけられるのは "良い" が "要素の数が多い" を意味するときだけです。また異なる再帰的関係を使えば実行時間を $O(n^{2})$ にできます。^[return]
このことから、モールス信号は・, $-$, ポーズの三つの符号からなる接頭独立な三進符号と言った方がより良い説明になります。あるいはモールス信号が一拍の音/光/流れ/高電圧/煙/ガス ($\blacksquare$) と一拍の無音/暗闇/地面/低電圧/空気/液体 ($\square$) からなる二進符号で、"トン" が $\blacksquare \square$ 、"ツー" が $\blacksquare \blacksquare \blacksquare \square$ に対応しているとみなせば、この符号は接頭独立となります。例えば文字列 "MORSE CODE" は次のように曖昧さ無しに符号化できます: ${\tiny \blacksquare\blacksquare\blacksquare\square\blacksquare\blacksquare\blacksquare}$${\tiny\square\square\square\blacksquare\blacksquare\blacksquare\square\blacksquare\blacksquare\blacksquare\square\blacksquare}$${\tiny\blacksquare\blacksquare\square\square\square\blacksquare\square\blacksquare\blacksquare\blacksquare\square\square\square}$${\tiny\blacksquare\square\blacksquare\square\blacksquare\square\square\square\blacksquare\square\square\square\square\square}$${\tiny\square\square\blacksquare\blacksquare\blacksquare\square\blacksquare\square\blacksquare\blacksquare\blacksquare\square}$${\tiny\blacksquare\square\square\square\blacksquare\blacksquare\blacksquare\square\blacksquare\blacksquare\blacksquare\square}$${\tiny\blacksquare\blacksquare\blacksquare\square\square\square\blacksquare\blacksquare\blacksquare\square\blacksquare\square}$${\tiny\blacksquare\square\square\square\blacksquare}$^[return]
Huffman は当時 Robert Fano (ロバート・ファノ) が担当する情報理論の講義の学生でした。Robert Fano は情報理論の父でもある Claude Shannon (クロード・シャノン) と親しい同僚であり、二人はそれまでに接頭符号を構築する別の貪欲アルゴリズム ――頻度配列をなるべく公平に二つに分け、それぞれについて符号を生成するというもの―― を考案していましたが、この Fano-Shannon 符号は最適でないことが知られていました。Fano は自分の講義で最適接頭符号を見つける問題を紹介し、それを見た Huffman は最終試験を受ける代わりにこの問題を講義の最終課題として解くことを決めたのですが、彼はこの問題が未解決であることも、 Fano と Shannon が解こうとして失敗していたことも知りませんでした。彼は数か月に渡って試行錯誤しましたが成果は上がらず、ついに諦めて最終試験を受けることに決めてノートをゴミ箱に入れたちょうどそのとき、解がひらめいたと言います。Huffman は後にこのひらめきのことを「突然の解明をもたらす決定的な稲妻 (the absolute lightning of sudden realization)」と表現しています。^[return]
この文章が最初に発表されたのは Alexander Dewdney (アレクサンダー・デュードニー) によって書かれ 1984 年に Scientific American に掲載された "Computer Recreations" コラムです。 Sallows 自身もこの文章の発見に関する興味深い物語を、いくつかの自己解説的な文章と共に 1985 年に出版しています。Sallows の論文は彼のウェブサイトで見ることができます。VAX 11 / 780 で自分のコードを実行したときの実行速度が気に入らなかった Sallows は、少しずつ文章を変えながら総当たりで ("This pangram has..." や "This sentence contains exactly..." など) 自己解説的な文章を探索する専用ハードウェアの設計さえ行いました。さらに注意深い理論的な解析によって探索空間が 60 億程度まで落ちたので、1-MHz で動く彼の Pangram Machine は二時間もかからずに全てチェックできたと言います。^[return]
Huffman と Fano にとっても驚きだったのは間違いありません！^[return]
アメリカの (少なくとも情報科学の) アカデミアにおける求人市場でも似たようなギャンブルが生じます。早くも二月から決断のための締め切りが二週間の勧誘を開始する機関もあれば、三月まで面接も始めない機関もありますし、悪名高い MIT のように五月になって全ての面接が終了するまで全ての学部が一切のオファーを行わない機関もあります。言うまでもなく、勧誘とその決断の締め切りが統一されていないのは求職者と機関にとって大きなストレスです。似たような理由から、1965 年以降アメリカの大学は 4 月 15 日という共通の日付を将来の大学院生の経済的支援 (および入学) の申し込みを受け付ける締め切りとしています。^[return]
現実ではほとんどの病院は複数のインターンを募集し、医師/病院は病院/医師の一部に対してだけランク付けを行い (この例を練習問題で見ます)、医師の数より募集されるインターンの方が多くなります。そのため問題はもっと複雑になります。^[return]
この例は Donald Knuth によって発見されました。^[return]
Boston Pool のアルゴリズムは Gale-Shapley のアルゴリズムの特殊ケースであり、オファーを特定の順番で出すようにしたものです。一言で言うと、次にオファーを出す病院は「まだオファーを断っていない医師の中で一番ランクが高い医師からのランク付けが一番高い病院」と決まっています。この方法だと次にオファーを出す病院がランク表全体に依存するので、アルゴリズムは必ず中央機関によって実行される必要があります。これに対して Gale-Shapley のアルゴリズムはランク表全体を事前に知っておく必要がなく、さらに言えば各病院/医師が事前にランク付けを完成させる必要さえありません。実行中に出されるクエリに対して一貫して答えるなら、それだけでアルゴリズムは正しく動きます。^[return]
このトンネルが参考にしたのはもちろん、Maciej Cegłowski が構想した Alameda-Weehauken ブリトートンネルです (https://idlewords.com/2007/04/the_alameda_weehawken_burrito_tunnel.htm)。^[return]
ドイツ語で言うなら Die Transkontinentaluntergrundburritolieferfahrzeugbatteriewechseltechnikervereinigung です。^[return]