Huffman 符号

二進符号 (binary code) は \(0\) と \(1\) からなる文字列 (符号) をアルファベットに対応させます。任意の符号が他の符号の接頭語になっていないとき、その二進符号は接頭独立 (prefix-free) であると言います (紛らわしいのですが、接頭独立な符号は接頭符号 (prefix code) と呼ばれることが多いです)。例えば 7 ビット ASCII コードと Unicode の UTF-8 はどちらも接頭独立な二進符号です。一方モールス信号は \(\cdot\) と \(-\) から構成されるものの、\(\color{maroon}{\texttt{E}}\) (・) が \(\color{maroon}{\texttt{I}}\) (・・) と \(\color{maroon}{\texttt{S}}\) (・・・) と \(\color{maroon}{\texttt{H}}\) (・・・・) の接頭語なので接頭独立ではありません¹。

接頭独立な二進符号は葉が文字に対応する二分木を使って可視化でき、そのとき葉の文字に対する符号は根からその葉までの道によって表されます。つまり、根から葉へ向かう道をたどって行って、左に曲がったときに \(0\) 、右に曲がったときに \(1\) を書いていくと、出来上がる文字列がその文字に対する符号となります。ここから文字の符号の長さは対応する葉の深さと等しいことが分かります。二分符号木と二分探索木は外見では似ていますが、同じではありません。二分符号木では葉に対応する文字が並ぶ順番を全く気にしないからです。

\(n\) 文字のアルファベットからなる文章を最小の符号で符号化したいとします。つまり、頻度を表す配列 \(f[1..n]\) が与えられたときに、接頭独立な二進符号であって、次の式で表される符号化された文章の長さを最小にするものを求めたいということです: \[ \sum_{i=1}^{n} f[i] \cdot \mathit{depth}(i) \] このコスト関数は最適二分探索木のときに考えたものと全く同じですが、最適化問題における制約が異なっています。二分符号木では葉の順番に関する制約が全くありません。

MIT の Ph.D. 生だった David Huffman (デイヴィッド・ハフマン) は 1951 年、最適な符号を生成するための次の貪欲アルゴリズムを発見しました²:

Huffman のアルゴリズムは例を使った方が分かりやすいでしょう。次に示すのは Lee Shallows (リー・サローズ) によって発見された、符号化を説明するのにとても都合がいい自己解説的 (self-descriptive) な文章です:³

解析を単純にするために 44 個のスペースと 19 個のアポストロフィと 19 個のコンマと 3 個のハイフンと 1 個のピリオドは無視して、さらに大文字だけを考えることにします。つまり、次の scriptio continua のような文字列だけを符号化の対象として考えるということです: \[ \begin{gathered} \color{maroon}{\texttt{THISSENTENCECONTAINSTHREEASTHREECSTWODSTWENTYSIXESFIVEFST}} \\ \color{maroon}{\texttt{HREEGSEIGHTHSTHIRTEENISTWOLSSIXTEENNSNINEOSSIXRSTWENTYSEV}} \\ \color{maroon}{\texttt{ENSSTWENTYTWOTSTWOUSFIVEVSEIGHTWSFOURXSFIVEYSANDONLYONEZ}} \end{gathered} \]

Sallow の文章に含まれる文字の頻度を表にすると次のようになります: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \color{maroon}{\texttt{A}} & \color{maroon}{\texttt{C}} & \color{maroon}{\texttt{D}} & \color{maroon}{\texttt{E}} & \color{maroon}{\texttt{F}} & \color{maroon}{\texttt{G}} & \color{maroon}{\texttt{H}} & \color{maroon}{\texttt{I}} & \color{maroon}{\texttt{L}} & \color{maroon}{\texttt{N}} & \color{maroon}{\texttt{O}} & \color{maroon}{\texttt{R}} & \color{maroon}{\texttt{S}} & \color{maroon}{\texttt{T}} & \color{maroon}{\texttt{U}} & \color{maroon}{\texttt{V}} & \color{maroon}{\texttt{W}} & \color{maroon}{\texttt{X}} & \color{maroon}{\texttt{Y}} & \color{maroon}{\texttt{Z}} \\ \hline 3 & 3 & 2 & 26 & 5 & 3 & 8 & 13 & 2 & 16 & 9 & 6 & 27 & 22 & 2 & 5 & 8 & 4 & 5 & 1 \\ \hline \end{array} \]

Huffman のアルゴリズムは最も頻度の低い二つの文字を選んでマージし、新しい文字とします。このとき頻度が同じ文字があるならどれを選んでも構いません。この例ではまず \(\color{maroon}{\texttt{Z}}\) と \(\color{maroon}{\texttt{D}}\) がマージされて新しく頻度 3 の文字 \(\color{maroon}{\texttt{DZ}}\) となります。構築している木にこの新しい文字を表す頂点が加わり、\(\color{maroon}{\texttt{Z}}\) と \(\color{maroon}{\texttt{D}}\) がその頂点の子となります。このとき二つの子のどちらが \(\color{maroon}{\texttt{Z}}\) でどちらが \(\color{maroon}{\texttt{D}}\) かは出来上がる符号の最適性に関係ありません。マージの後 Huffman のアルゴリズムは頻度表を更新します: \[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \color{maroon}{\texttt{A}} & \color{maroon}{\texttt{C}} & \color{maroon}{\texttt{E}} & \color{maroon}{\texttt{F}} & \color{maroon}{\texttt{G}} & \color{maroon}{\texttt{H}} & \color{maroon}{\texttt{I}} & \color{maroon}{\texttt{L}} & \color{maroon}{\texttt{N}} & \color{maroon}{\texttt{O}} & \color{maroon}{\texttt{R}} & \color{maroon}{\texttt{S}} & \color{maroon}{\texttt{T}} & \color{maroon}{\texttt{U}} & \color{maroon}{\texttt{V}} & \color{maroon}{\texttt{W}} & \color{maroon}{\texttt{X}} & \color{maroon}{\texttt{Y}} & \color{maroon}{\texttt{DZ}} \\ \hline 3 & 3 & 26 & 5 & 3 & 8 & 13 & 2 & 16 & 9 & 6 & 27 & 22 & 2 & 5 & 8 & 4 & 5 & 3 \\ \hline \end{array} \]

再帰的に 19 回のマージを行うと 20 個の文字が一つの頂点にマージされ、マージされた様子を図示すると符号木となります。このアルゴリズムには何をするかを自由に選べる場面が何度もあるので、同じ頻度表に対する Huffman 符号はいくつも存在します。この例に対する Huffman 符号の一つを次に示します。葉でない頂点にはマージした文字の頻度の和が書かれています。例えば \(\color{maroon}{\texttt{A}}\) に対する符号は \(\color{#2D2F91}{\texttt{101000}}\) で、\(\color{maroon}{\texttt{S}}\) に対する符号は \(\color{#2D2F91}{\texttt{111}}\) です:

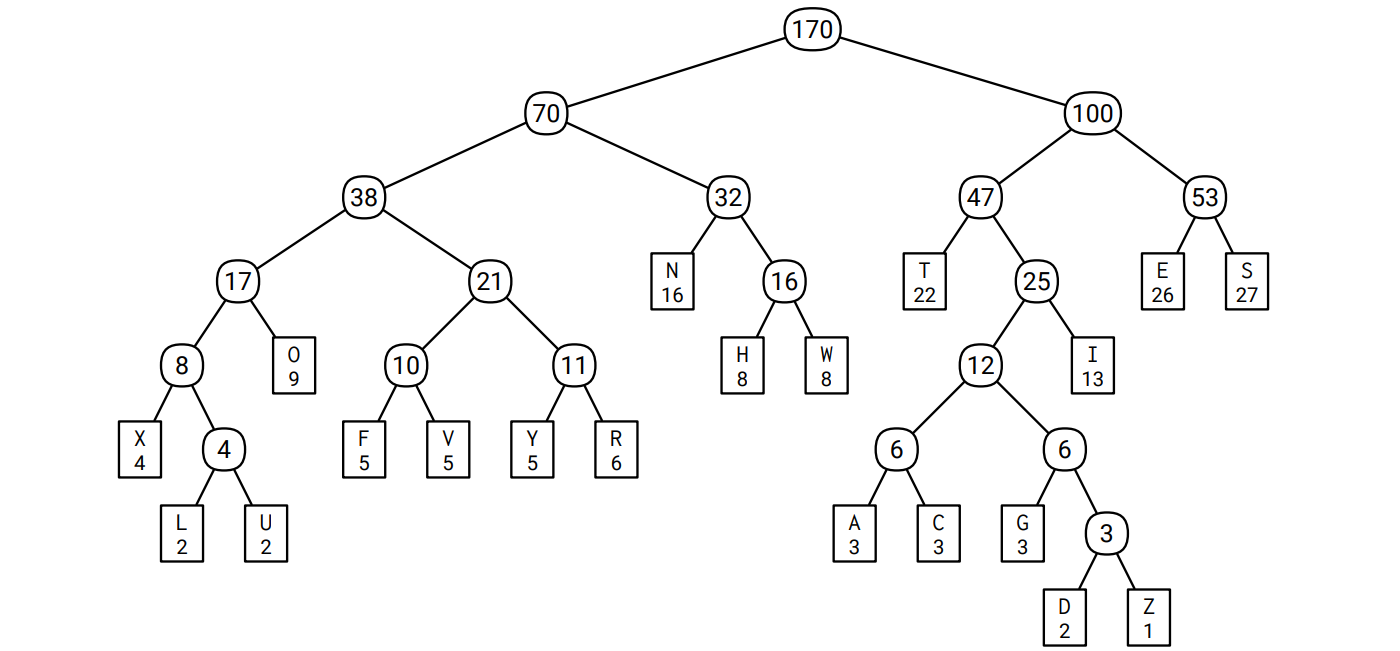
この Huffman 符号を使って Sallows の文章を符号化すると次のようになります: \[ \small \frac{\color{#2D2F91}\texttt{100}}{\color{#B52F1B}\texttt{T}} \frac{\color{#2D2F91}\texttt{0110}}{\color{#B52F1B}\texttt{H}} \frac{\color{#2D2F91}\texttt{1011}}{\color{#B52F1B}\texttt{I}} \frac{\color{#2D2F91}\texttt{111}}{\color{#B52F1B}\texttt{S}} \frac{\color{#2D2F91}\texttt{111}}{\color{#B52F1B}\texttt{S}} \frac{\color{#2D2F91}\texttt{110}}{\color{#B52F1B}\texttt{E}} \frac{\color{#2D2F91}\texttt{010}}{\color{#B52F1B}\texttt{N}} \frac{\color{#2D2F91}\texttt{100}}{\color{#B52F1B}\texttt{T}} \frac{\color{#2D2F91}\texttt{110}}{\color{#B52F1B}\texttt{E}} \frac{\color{#2D2F91}\texttt{010}}{\color{#B52F1B}\texttt{N}} \frac{\color{#2D2F91}\texttt{101001}}{\color{#B52F1B}\texttt{C}} \frac{\color{#2D2F91}\texttt{110}}{\color{#B52F1B}\texttt{E}} \frac{\color{#2D2F91}\texttt{101001}}{\color{#B52F1B}\texttt{C}} \frac{\color{#2D2F91}\texttt{0001}}{\color{#B52F1B}\texttt{O}} \frac{\color{#2D2F91}\texttt{010}}{\color{#B52F1B}\texttt{N}} \frac{\color{#2D2F91}\texttt{100}}{\color{#B52F1B}\texttt{T}} \cdots \]

各アルファベットの Sallows の文章での出現頻度、Huffman 符号におけるコスト、Sallows の文章全体を符号化したときの全体の長さへの寄与を次の表にまとめます: \[ \small \def\arraystretch{1.2} \begin{array}{|c|c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c:c|} \hline \text{char} & \texttt{\color{#B52F1B}A} & \texttt{\color{#B52F1B}C} & \texttt{\color{#B52F1B}D} & \texttt{\color{#B52F1B}E} & \texttt{\color{#B52F1B}F} & \texttt{\color{#B52F1B}G} & \texttt{\color{#B52F1B}H} & \texttt{\color{#B52F1B}I} & \texttt{\color{#B52F1B}L} & \texttt{\color{#B52F1B}N} & \texttt{\color{#B52F1B}O} & \texttt{\color{#B52F1B}R} & \texttt{\color{#B52F1B}S} & \texttt{\color{#B52F1B}T} & \texttt{\color{#B52F1B}U} & \texttt{\color{#B52F1B}V} & \texttt{\color{#B52F1B}W} & \texttt{\color{#B52F1B}X} & \texttt{\color{#B52F1B}Y} & \texttt{\color{#B52F1B}Z} \\ \hline \text{freq} & 3 & 3 & 2 & 26 & 5 & 3 & 8 & 13 & 2 & 16 & 9 & 6 & 27 & 22 & 2 & 5 & 8 & 4 & 5 & 1 \\ \hdashline \text{depth} & 6 & 6 & 7 & 3 & 5 & 6 & 4 & 4 & 6 & 3 & 4 & 5 & 3 & 3 & 6 & 5 & 4 & 5 & 5 & 7 \\ \hdashline \text{total} & 18 & 18 & 14 & 78 & 25 & 18 & 32 & 52 & 12 & 48 & 36 & 30 & 81 & 66 & 12 & 25 & 32 & 20 & 25 & \hspace{0.25em}7\hspace{0.25em} \\ \hline \end{array} \]

この Huffman 符号で文章全体を符号化したときの長さは 649 ビットです。異なる Huffman 符号では同じ文字に違う符号が割り当てられ、符号の長さが違うことさえあり得ます。しかしそれでも、全ての Huffman 符号は文章全体を 649 ビットという同じ長さで符号化します。

Huffman のアルゴリズムはとても単純なので、このアルゴリズムが最適な接頭独立二進符号を生成するというのは驚きです⁴。Sallows の文章をどんな接頭独立二進符号で符号化したとしても、最低 649 ビットかかるというのです！ しかし幸いにもこのアルゴリズムは再帰的なので、これまでの最適性の証明で使ってきた交換の議論を使えば証明は簡単です。まずアルゴリズムの最初の選択が正しいことを示すことから始めます。

ここまでくれば、最適性は私たちの親愛なる友人である再帰の妖精によって保証されます！再帰的な議論は次の少し変わった全二分木の定義によって行われます: 「全二分木はただ一つの頂点からなる木であるか、そうでなければ、全二分木の任意の葉を二つの葉を子として持つ頂点と交換した木である」

効率的に Huffman 符号を構築するには、文字の頻度を優先度とした優先度付きキューを使うと上手く行きます。また出来上がった符号木を表すには、各頂点の左の子、右の子、親、を格納した三つの添え字配列を使うと便利です。最終的な符号木における葉は \(1\) から \(n\) までの添え字で表され、根は \(2n-1\) の添え字で表されます。

Huffman のアルゴリズムの疑似コードを以下に示します。 \(\textsc{BuildHuffman}\) は \(O(n)\) 回の優先度付きキューの操作を行います: 正確には \(\textsc{Insert}\) を \(2n-1\) 回、\(\textsc{ExtractMin}\) を \(2n-2\) 回です。優先度付きキューを通常の二分ヒープを使って実装すれば各操作の実行時間は \(O(\log n)\) なので、アルゴリズム全体の実行時間は \(\pmb{O(n \log n)}\) です。

最後に、構築された符号木で文章の符号化/複合化を行う単純なアルゴリズムを示します。符号化後の文章の長さを \(m\) とすると、実行時間はどちらも \(O(m)\) です。

1. このことから、モールス信号は ・, \(-\), ポーズの三つの符号からなる接頭独立な三進符号と言った方がより良い説明になります。あるいはモールス信号が一拍の音/光/流れ/高電圧/煙/ガス (\(\blacksquare\)) と一拍の無音/暗闇/地面/低電圧/空気/液体 (\(\square\)) からなる二進符号で、"トン" が \(\blacksquare \square\) 、"ツー" が \(\blacksquare \blacksquare \blacksquare \square\) に対応しているとみなせば、この符号は接頭独立となります。例えば文字列 "MORSE CODE" は次のように曖昧さ無しに符号化できます: \({\tiny \blacksquare\blacksquare\blacksquare\square\blacksquare\blacksquare\blacksquare}\)\({\tiny\square\square\square\blacksquare\blacksquare\blacksquare\square\blacksquare\blacksquare\blacksquare\square\blacksquare}\)\({\tiny\blacksquare\blacksquare\square\square\square\blacksquare\square\blacksquare\blacksquare\blacksquare\square\square\square}\)\({\tiny\blacksquare\square\blacksquare\square\blacksquare\square\square\square\blacksquare\square\square\square\square\square}\)\({\tiny\square\square\blacksquare\blacksquare\blacksquare\square\blacksquare\square\blacksquare\blacksquare\blacksquare\square}\)\({\tiny\blacksquare\square\square\square\blacksquare\blacksquare\blacksquare\square\blacksquare\blacksquare\blacksquare\square}\)\({\tiny\blacksquare\blacksquare\blacksquare\square\square\square\blacksquare\blacksquare\blacksquare\square\blacksquare\square}\)\({\tiny\blacksquare\square\square\square\blacksquare}\)^[return]

2. Huffman は当時 Robert Fano (ロバート・ファノ) が担当する情報理論の講義の学生でした。Robert Fano は情報理論の父でもある Claude Shannon (クロード・シャノン) と親しい同僚であり、二人はそれまでに接頭符号を構築する別の貪欲アルゴリズム ――頻度配列をなるべく公平に二つに分け、それぞれについて符号を生成するというもの―― を考案していましたが、この Fano-Shannon 符号は最適でないことが知られていました。Fano は自分の講義で最適接頭符号を見つける問題を紹介し、それを見た Huffman は最終試験を受ける代わりにこの問題を講義の最終課題として解くことを決めたのですが、彼はこの問題が未解決であることも、 Fano と Shannon が解こうとして失敗していたことも知りませんでした。彼は数か月に渡って試行錯誤しましたが成果は上がらず、ついに諦めて最終試験を受けることに決めてノートをゴミ箱に入れたちょうどそのとき、解がひらめいたと言います。Huffman は後にこのひらめきのことを「突然の解明をもたらす決定的な稲妻 (the absolute lightning of sudden realization)」と表現しています。^[return]

3. この文章が最初に発表されたのは Alexander Dewdney (アレクサンダー・デュードニー) によって書かれ 1984 年に Scientific American に掲載された "Computer Recreations" コラムです。 Sallows 自身もこの文章の発見に関する興味深い物語を、いくつかの自己解説的な文章と共に 1985 年に出版しています。Sallows の論文は彼のウェブサイトで見ることができます。VAX 11 / 780 で自分のコードを実行したときの実行速度が気に入らなかった Sallows は、少しずつ文章を変えながら総当たりで ("This pangram has..." や "This sentence contains exactly..." など) 自己解説的な文章を探索する専用ハードウェアの設計さえ行いました。さらに注意深い理論的な解析によって探索空間が 60 億程度まで落ちたので、1-MHz で動く彼の Pangram Machine は二時間もかからずに全てチェックできたと言います。^[return]

4. Huffman と Fano にとっても驚きだったのは間違いありません！^[return]