最大フローと最小カット
処理を止めてしまってはそれを理解することはできない。処理の理解はその流れとともに形を変え、流れと共に流れなければならない。
予想に反して、フローは余暇や娯楽でリラックスしているときには起きない。精神的・肉体的な能力が試されるような難しい仕事に積極的に取り組んでいるときにこそ、フローは訪れる...フローを努力無しに達成するのは難しい。フローは "時間の無駄" ではない。
道を知っていても、道を歩いたことにはならない。
1950 年代の中頃、米空軍の研究者 Theodore E. Harris (セオドア・E・ハリス) と米陸軍退役将校 Frank S. Ross (フランク・S・ロス) は、ソ連とその衛星国を結ぶ東ヨーロッパの鉄道ネットワークに関する機密レポートを作成しました。ネットワークは頂点を 44 個持つ辺に重みの付いたグラフとしてモデル化され、頂点が地域を、辺の重みが地域の間を輸送できる資源の量を表します。彼らは本質的には総当たりと変わらない方法を使って、ネットワークにおいてロシアからヨーロッパへ輸送できる資源の最大量、および最低限の辺を削除 (具体的に言うと、線路を爆破) してネットワークを崩壊させる方法を発見しました。この爆破すべき線路のことは「ボトルネック (bottleneck)」と呼ばれました。彼らのレポートに含まれる図を次に示します。このレポートの機密指定が解かれたのはやっと 1999 年のことです1。
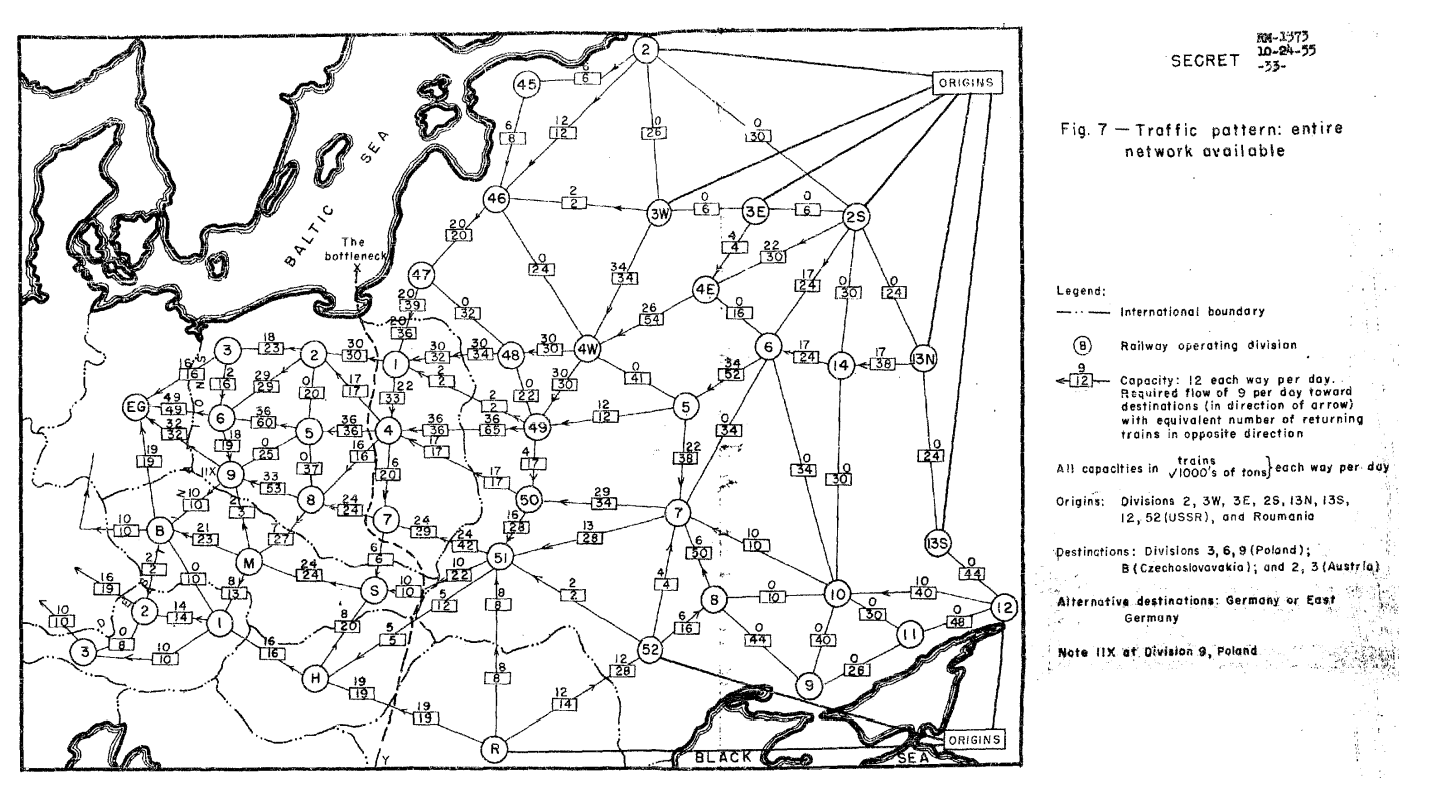
これは最大フロー (maximum flow) 問題と最小カット (minimum cut) 問題の記録に残っている範囲で最も古い応用の一つです。両方の問題において入力は有向グラフ \(G=(V,E)\) とソース (source) 頂点 \(s\) と シンク (sink) 頂点 \(t\) の三つです。直感的に言えば、最大フロー問題は \(s\) から \(t\) に輸送できる資源の最大量を計算し、最小カット問題は \(s\) と \(t\) を切り離すために必要なダメージの最小値を計算します。
フロー
\(\pmb{(s, t)}\)-フロー (ソースとシンクが明らかな場合には単にフロー) とは、関数 \(f:E \rightarrow \mathbb{R}\) であって \(s,t\) 以外の全ての頂点 \(v\) において次の保存条件 (conservation constraint) が満たされるものを言います: \[ \sum_{u} f(u \rightarrow v) = \sum_{w} f(v \rightarrow w) \]
保存条件を言葉を使って言い換えれば、全ての頂点 \(v\) に対して \(v\) に入るフローと \(v\) から出るフローが等しいということです。記法を単純にするために、辺 \(u \rightarrow v\) が存在しない場合には \(f(u \rightarrow v) = 0\) と定義します。フロー \(f\) の値 (value) \(|f|\) とはソース頂点 \(s\) から出るフローの和です: \[ |f| := \sum_{w} f(s \rightarrow w) - \sum_{u} f(u \rightarrow s) \]
\(|f|\) がシンク頂点 \(t\) へ向かうフローの和とも等しいことを示すのは難しくありません。記法を単純にするために、\(\pmb{\partial f(v)}\) で頂点 \(v\) から出るフローを表すことにします: \[ \partial f (v) := \sum_{w} f(v \rightarrow w) - \sum_{u} f(u \rightarrow v) \] 保存条件から \(s, t\) 以外の頂点 \(v\) について \(\partial f(v) = 0\) であり、したがって \[ \sum_{v} \partial f(v) = \partial f(s) + \partial f(t) \] です。一方で全てのフローはある頂点から出て他の頂点に入るので \(\sum_{v} \partial f (v) = 0\) であり、したがって \(|f| = \partial f(s) = - \partial f(t)\) が成り立ちます。
ここでグラフの辺に非負の容量 (capacity) を割り当てるもう一つの関数 \(c: E \rightarrow \mathbb{R}_{\geq 0}\) が追加で与えられたとします。フロー \(f\) が容量 \(c\) に対して実現可能 (feasible) であるとは、全ての辺 \(e\) に対して \(0 \leq f(e) \leq c(e)\) が成り立つことを言います。フローを考えると言った場合に通常考えるのは、何らかの固定された容量関数 \(c\) に対する実現可能なフローです。またフロー \(f\) と容量関数 \(c\) について、辺 \(e\) で \(f(e) = c(e)\) が成り立つならば \(f\) は \(e\) を 飽和 (saturate) させると言い、\(f(e) = 0\) ならば \(f\) は \(e\) を避ける (avoid) と言います。
最大フロー問題 (maximum flow problem) とは、与えられた有向グラフと容量関数に対する実現可能な \((s,t)\)-フローであって値が最大のものを計算する問題です。
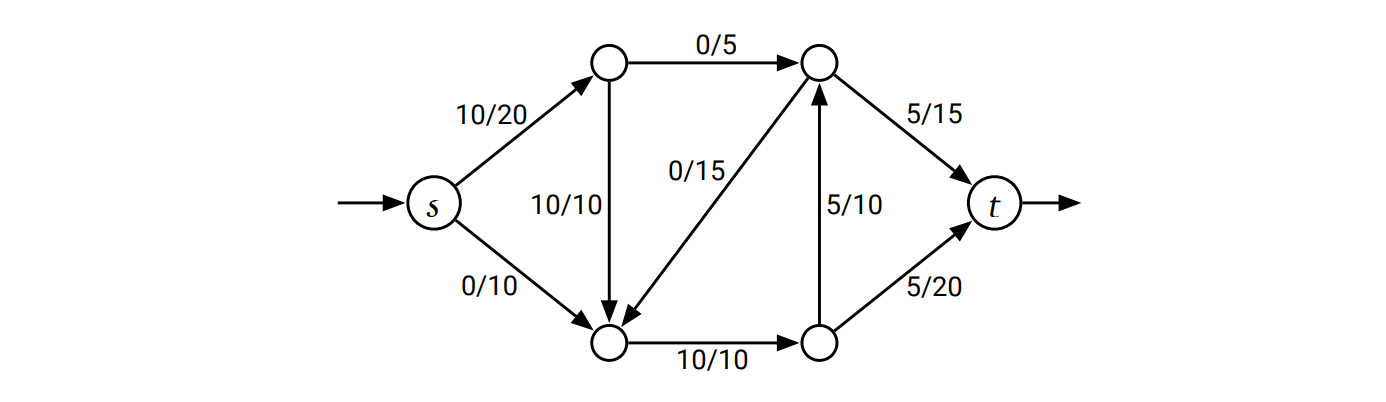
カット
\(\pmb{(s, t)}\)-カット (ソースとシンクが明らかな場合は単にカット) とは、頂点集合の互いに素な二つの部分集合 \(S, T\) への分解であって \(s \in S\) かつ \(t \in T\) を満たすものを言います。\(S\) と \(T\) が互いに素とは \(S \cup T = V\) かつ \(S \cap V = \varnothing\) ということです。
容量関数 \(c:E \rightarrow \mathbb{R}_{\geq 0}\) が与えられたとき、カットの容量 (capacity) が \(S\) から \(T\) に向かう辺の容量の和として定義されます: \[ \| S, T \| = \sum_{s \in S} \sum_{t \in T} c(s \rightarrow t) \] (ここでも辺 \(v \rightarrow w\) が存在しない場合には \(c(v \rightarrow w) = 0\) とします) この定義が非対称なことに注意してください。\(T\) から \(S\) に向かう辺はカウントしません。
最小カット問題 (minimum cut problem) とは、容量が最小の \((s,t)\)-カットを計算する問題です。
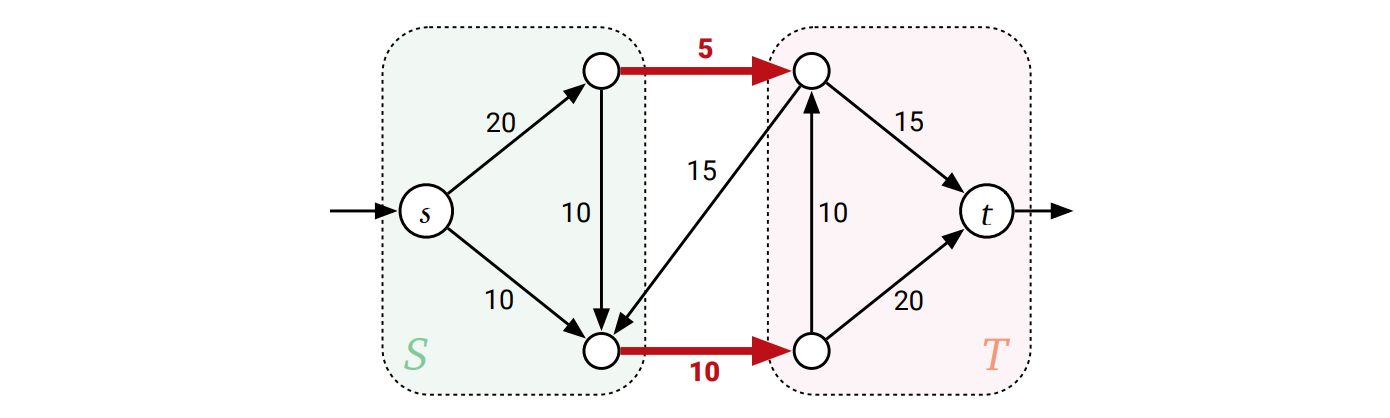
直感的に言えば、最小カットとは \(s\) から \(t\) への全てのフローを断ち切るための一番安価な方法です。フローとカットに関する次の関係を示すのは難しくありません:
命題 10.1 \(f\) を実現可能な任意の \((s,t)\)-フロー、\((S, T)\) を任意の \((s, t)\)-カットとする。このとき \(f\) の値は \((S, T)\) の容量以下である。また \(f\) が \(S\) から \(T\) へ向かう辺を全て飽和させてかつ \(T\) から \(S\) への全ての辺を避けることは \(|f| = \| S, T \|\) と同値である。
証明 任意の実現可能なフロー \(f\) とカット \((S, T)\) を取ると、次の不等式が成り立つ: \[ \begin{aligned} |f| & = \partial f (s) & [\text{定義}] \\ & = \sum_{v \in S} \partial f(v) & [\text{保存条件}] \\ & = \sum_{v \in S}\sum_{w} f(v \rightarrow w) - \sum_{v \in S} \sum_{u} f(u \rightarrow v) & [\partial \text{ の定義}] \\ & = \sum_{v \in S}\sum_{w \notin S} f(v \rightarrow w) - \sum_{v \in S} \sum_{u \notin S} f(u \rightarrow v) & [S \text{ から } S \text{ への辺を削除}] \\ & = \sum_{v \in S}\sum_{w \in T} f(v \rightarrow w) - \sum_{v \in S} \sum_{u \in T} f(u \rightarrow v) & [\text{カットの定義}] \\ & {\color{red}\leq} \sum_{v \in S}\sum_{w \in T} f(v \rightarrow w) & [f(u \rightarrow v) \geq 0] \\ & {\color{red}\leq} \sum_{v \in S}\sum_{w \in T} c(v \rightarrow w) & [f(u \rightarrow v) \leq c(v \rightarrow w)] \\ & = \|S, T \| & [\text{定義}] \end{aligned} \]
二つ目のステップでは、全ての頂点 \(v \in S \backslash \lbrace s \rbrace\) において \(\partial f(v) = 0\) なことからゼロを足しているだけである。また四つ目のステップでは全ての \(x, y \in S\) に対するフローの値 \(f(x \rightarrow y)\) を削除しているが、これが可能なのはこの値が二つの和の両方で出現するためである。つまり、\(v = x\) と \(w = y\) のときに一度、\(v = y\) と \(u = x\) のときに一度出現する。
式変形中の最初の不等号は \(f\) が \(T\) から \(S\) への辺を全て避けるときに限って等号となる。同様に二つ目の不等号は \(f\) が \(T\) から \(S\) への辺を全て飽和させるときに限って等号となる。 \(\Box\)
この命題から、もし \(|f| = \| S, T \|\) ならば \(f\) が最大フローで \((S, T)\) が最小カットであることが分かります。
最大フロー最小カット定理
意外なことに、任意のフローネットワークは \(|f| = \| S, T \|\) を満たす \((s,t)\)-フロー \(f\) と \((s,t)\)-カット \((S, T)\) を必ず持ちます。これが有名な最大フロー最小カット定理 (Maxflow-Mincut Theorem) です。この定理は Lester Ford (レスター・フォード、最短路アルゴリズムで知られる) と Delbert Fulkerson (デルバート・ファルカーソン) によって 1954 年に初めて証明され、1956 年には Peter Elias (ピーター・イライアス) と Amiel Feinstein (アミエイ・ファインスタイン) と Claude Shannon (クロード・シャノン、迷路を解くロボットと情報理論で知られる) によって独立に証明されています。
最大フロー最小カット定理 ソース \(s\) からシンク \(t\) への任意のフローネットワークにおいて、\((s,t)\)-フローの最大値と \((s,t)\)-カットの最小容量は等しい。
これから示すのは Ford と Fulkerson が行った証明です。\(G\) を任意のグラフ、\(s, t\) を \(G\) の適当な頂点、\(c:E \rightarrow \mathbb{R}_{\geq 0}\) を容量関数とします。証明はグラフが既約 (reduced) であること、つまり \(u\) と \(v\) の間には最大でも一つの辺しかないことを仮定すると簡単になります。既約という条件を言い換えると、任意の \(u \rightarrow v\) について \(c(u \rightarrow v) = 0\) または \(c( v \rightarrow u) = 0\) の少なくとも一方が必ず成り立つということです。この仮定は任意のグラフに対して簡単に強制できます: \(G\) の全ての辺に対して新しい頂点 \(x\) を追加し、 \(u \rightarrow v\) という辺を \(u \rightarrow x \rightarrow v\) という路に入れ替え、\(c(u \rightarrow x) =\) \(c (x \rightarrow v) = \) \(c(u \rightarrow v)\) と定義すると、改変されたグラフは元のグラフと同じ最大フローの値と最小カットの容量を持つ既約なグラフとなるためです。

\(G\) における任意の実現可能な \((s,t)\)-フローを \(f\) とし、\(f\) に対応する新しい容量関数 \(c_{f} : V \times V \rightarrow \mathbb{R}\) を次のように定義します。この容量関数を残余容量 (residual capacity) と呼びます: \[ c_{f} (u \rightarrow v) = \begin{cases} c(u \rightarrow v) - f (u \rightarrow v) & \text{if } u \rightarrow v \in E \\ f(v \rightarrow u) & \text{if } v \rightarrow u \in E \\ 0 & \text{それ以外} \end{cases} \] 直感的に言えば、ある辺の残余容量は現在その辺に流れている値に追加して流すことのできるフローの量を表します。\(f \geq 0\) かつ \(f \leq c\) なので残余容量の値は非負です。
元のグラフ \(G\) に辺 \(u \rightarrow v\) が存在しなかったとしても \(c_{f}(u \rightarrow v) > 0\) となることがあり得ます。そのため \(E_{f}\) を残余容量が正である辺の集合とすると、\(G_{f} = (V, E_{f})\) は (\(G\) と異なるグラフである)残余グラフ (residual graph) を定義します。ほとんどの場合において、残余グラフは既約ではありません。具体的には \(0 < f ( u \rightarrow v) < c(u \rightarrow v) \) が成り立つとき、残余グラフ \(G_{f}\) には辺 \(u \rightarrow v\) と辺 \(v \rightarrow u\) の両方が含まれます。
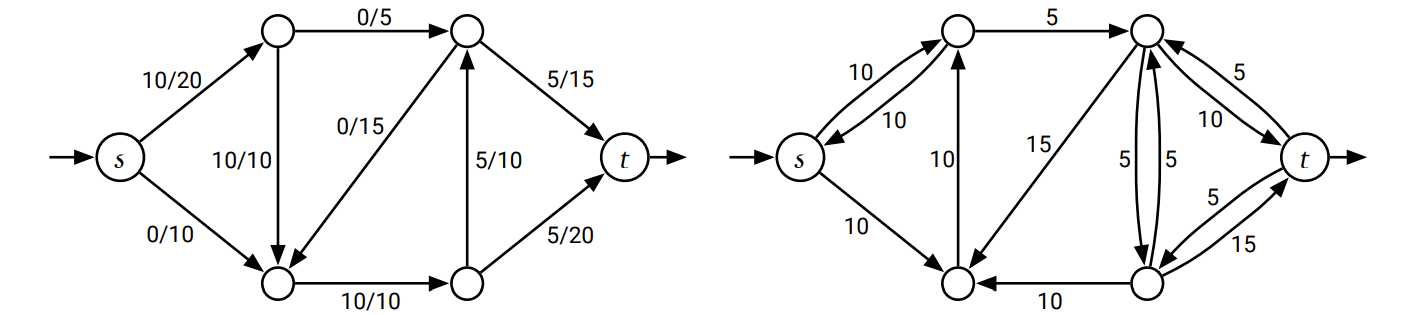
ここで考えるべきケースが二つあります。一つは残余グラフに \(G_{f}\) にソース頂点 \(s\) からシンク頂点 \(t\) までの有向路が存在する場合で、もう一つはそのような有向路が存在しない場合です。
まず残余グラフ \(G_{f}\) に \(s\) から \(t\) への有向路 \(P\) が存在するとします。このような路 \(P\) を増加路 (augumenting path) と呼びます。\(P\) に流せる最大のフローを \(\displaystyle F = \min_{u \rightarrow v \in P} c_{f} (u \rightarrow v)\) とし、(元のグラフにおける) 新しいフロー \(f^{\prime}: E \rightarrow \mathbb{R}\) を次のように定義します: \[ f^{\prime}(u \rightarrow v) = \begin{cases} f(u \rightarrow v) + F & \text{if } u \rightarrow v \in P \\ f(u \rightarrow v) - F & \text{if } v \rightarrow u \in P \\ f(u \rightarrow v) & \text{それ以外} \end{cases} \]
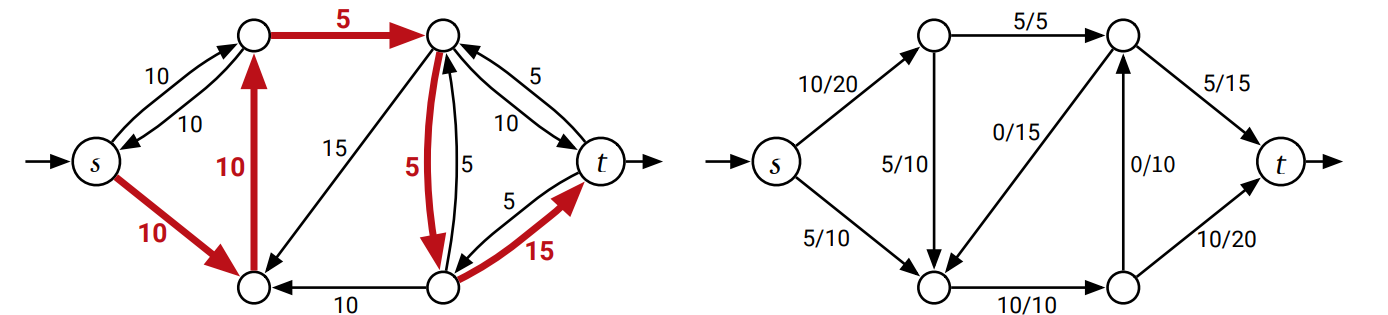
この新しいフロー \(f^{\prime}\) が元の容量 \(c\) に対して実現可能であること、つまり全ての辺に対して \(f^{\prime} \geq 0\) かつ \(f^{\prime} \leq c\) であることをこれから示します。元のグラフ \(G\) における辺 \(u \rightarrow v\) に対する三つのケースを考えます:
-
\(P\) が \(u \rightarrow v\) を含むならば、\(f\) が実現可能なことより \[ f^{\prime} (u \rightarrow v) = f(u \rightarrow v) + F > f(u \rightarrow v) \geq 0 \] であり、また \[ \begin{aligned} f^{\prime} (u \rightarrow v) & = f(u \rightarrow v) + F && [f^{\prime} \text{ の定義}] \\ & \leq f(u \rightarrow v) + c_{f}(u \rightarrow v) && [F \text{ の定義}] \\ & = f(u \rightarrow v) + c(u \rightarrow v) - f(u \rightarrow v) && [c_{f} \text{ の定義}] \\ & = c(u \rightarrow v) && [\text{やったぜ}] \end{aligned} \] も成り立つ。
-
\(P\) が \(u \rightarrow v\) の逆 \(v \rightarrow u\) を含むならば、ここでも \(f\) が実現可能なことから \[ f^{\prime} (u \rightarrow v) = f(u \rightarrow v) - F < f(u \rightarrow v) \leq c(u \rightarrow v) \] であり、また \[ \begin{aligned} f^{\prime}(u \rightarrow v) & = f(u \rightarrow v) - F && [f^{\prime} \text{ の定義}] \\ & \geq f(u \rightarrow v) - c_{f}(v \rightarrow u) && [F \text{ の定義}] \\ & = f(u \rightarrow v) - f(u \rightarrow v) && [c_{f} \text{ の定義}] \\ & = 0 && [\text{やったぜ}] \end{aligned} \] も成り立つ。
-
最後に \(u \rightarrow v\) も \(v \rightarrow u\) も増加路に含まれないなら \(f^{\prime}(u \rightarrow v) = f(u \rightarrow v)\) だから、 \(f\) が実現可能なことより \(0 \leq f^{\prime}(u \rightarrow v) \leq c(u \rightarrow v)\) が成り立つ。
よって \(f^{\prime}\) は実現可能です。
最後に、増加路で \(s\) から離れる辺は最初の辺だけなので \(|f^{\prime}| = |f| + F > |f|\) であり、したがって \(f^{\prime}\) は \(f\) よりも大きな値を持つ実現可能なフローです。以上より、残余グラフ \(G_{f}\) に \(s\) から \(t\) への路が存在するならば \(f\) は最大フローではないと言えます。
一方で残余グラフ \(G_{f}\) に \(s\) から \(t\) への有向路が含まれないとします。このとき \(G_{f}\) で \(s\) から到達可能な頂点の集合を \(S\) とし、さらに \(T = V \backslash S\) と定めると、分割 \((S, T)\) は明らかに \((s,t)\)-カットとなります。さらに任意の \(u \in S\) と \(v \in T\) について \(c_{f}(u \rightarrow v) = 0\) なことから \[ \begin{cases} c(u \rightarrow v) - f (u \rightarrow v) = 0 & \text{if } u \rightarrow v \in E \\ f(v \rightarrow u) = 0 & \text{if } v \rightarrow u \in E \end{cases} \] が成り立ちます。これを言い換えると、考えているフロー \(f\) は \(S\) から \(T\) へ向かう辺を全て飽和させ、\(T\) から \(S\) に向かう辺を全て避けるということです。よって 命題 10.1 より \(|f| = \|S,T\|\) であり、 \(f\) が最大フローで \((S, T)\) が最小カットであることが分かります。
証明はこれで完了です! \(\Box\)
Ford と Fulkerson の増加路アルゴリズム
Ford と Fulkerson が示した最大フロー最小カット定理の証明から、最大フローを計算するアルゴリズムが直ちに手に入ります: 空のフローから始め、残余グラフにおける \(s\) から \(t\) への任意の増加路を使ってフローを増加させる処理を増加路が無くなるまで繰り返すというものです。
このアルゴリズムについての次の系は簡単に示せますが、重要です:
整数性定理 フローネットワークの辺の容量が全て整数ならば、全ての辺に流れるフローが整数の最大フローが存在する。
証明 増加路アルゴリズムの各反復が終わった時点における全ての残余容量が整数であることを帰納法で示す。
-
最初の反復の始まる前、フローの値は \(0\) (整数) であり、残余容量は元のネットワークの容量と等しい。元のネットワークの容量が整数であるという問題の仮定より残余容量は整数である。
-
各反復が始まる時点において、帰納法の仮定から増加路の容量 \(F\) は整数である。よって増加路を使ってフローを増加させたときの任意の辺のフローおよび残余容量の変化は必ず整数である。
したがって増加路アルゴリズムは各反復においてフローの値を正の整数分だけ増加させる。よってアルゴリズムは停止し、その出力が最大フローである。 \(\Box\)
実際の最大フローを \(f^{\ast}\) とすると、辺の容量が整数のネットワークに対する Ford-Fulkerson のアルゴリズムは大きく見積もっても最大 \(|f^{\ast}|\) 回の反復の後に停止します。各反復においてこのアルゴリズムは増加路を見つけるための何か優先探索と残余グラフ \(G_{f}\) の構築を \(O(E)\) 時間で行うので、この設定における最悪実行時間は \(\pmb{O(E|f^{\ast}|)}\) です。
Jack Edmonds と Richard Karp はこの実行時間解析が本質的に厳密であることを証明しました。次の図にある四つの頂点を持つネットワークを考えます。ここで \(X\) はとても大きい整数を表します。このネットワークにおける最大フローの値は明らかに \(2X\) です。しかし Ford-Fulkerson のアルゴリズムは増加路 \(s \rightarrow u \rightarrow v \rightarrow t\) を使って \(1\) だけフローを増加させ、その後増加路 \(s \rightarrow v \rightarrow u \rightarrow t\) を使って \(1\) だけフローを増加させるという処理を繰り返すかもしれません。この場合実行時間は \(\Theta(X) = \Omega(|f^{\ast}|)\) となります。
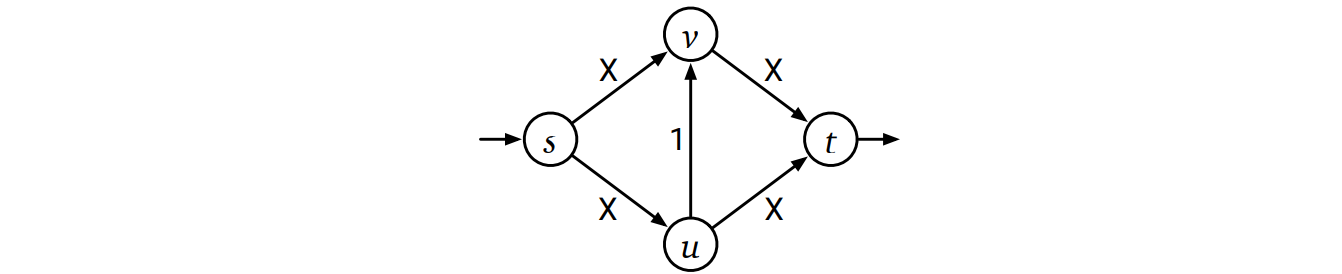
現実のデータから作られるグラフの多く、あるいは \(|f^{\ast}|\) が小さいという条件においては、Ford-Fulkerson のアルゴリズムはとても高速に動作します。しかし増加路に制限を設けなければ、最悪計算時間が効率的だとは言えません。Edmonds と Karp が示した上記のネットワークは \(O(\log X)\) ビットで表現できるので、Ford-Fulkerson の実行時間は実は入力サイズに対して指数的だからです。
無理数の容量
では容量が整数でなかったら? 容量に (正の) 定数をかければ最大フローは同じだけ大きくなるので、辺の重みが有理数の場合には Ford-Fulkerson のアルゴリズムを使って最大フローを求められます。ただしこの場合でも計算時間は (入力を表現するためのビット長に対して) 指数的です。
一方で無理数の容量がある場合、アルゴリズムがどんどん小さくなる増加路を選び続けて停止しないことがあります。さらに悪いことに、この増加していくフローの無限列が最大フローに収束しない、さらには最大フローからかけ離れた値に収束することがあります! この悪い振る舞いをするネットワークの最小の例は 1993 年に Uri Zwick (ユリ・ツウィック) によって発見されました3:
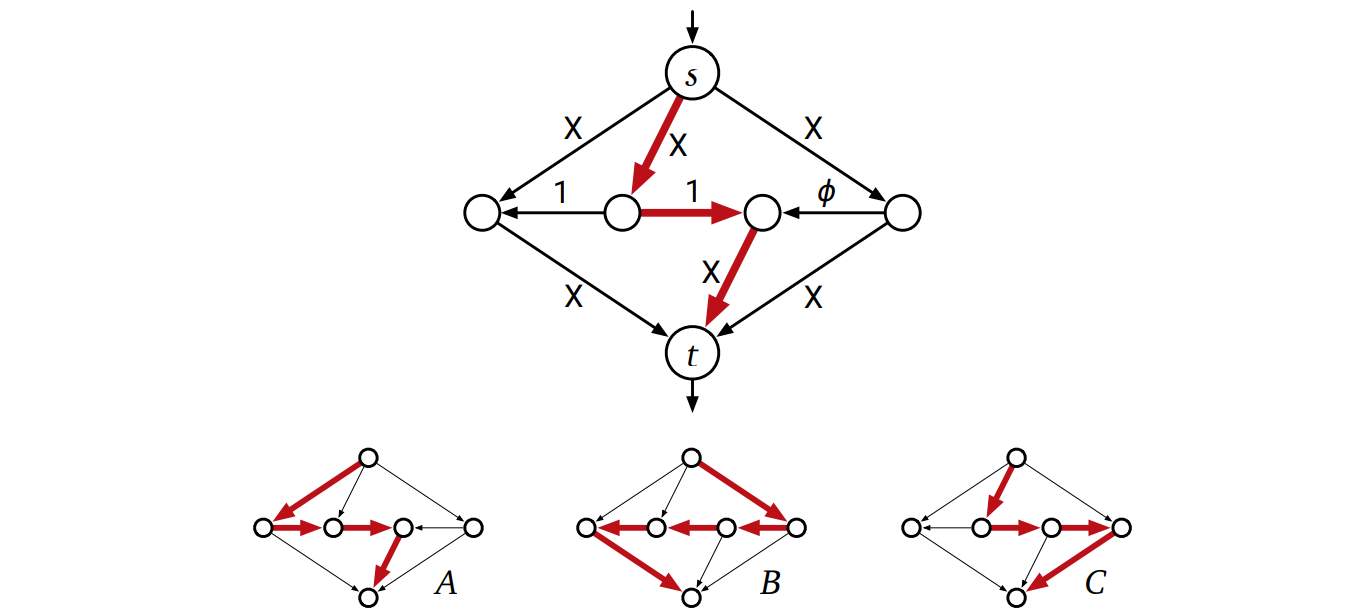
このネットワークに含まれる 9 個の辺のうち 6 個にはとても大きい整数の重み \(X\) が付いており、2 個には重み \(1\) が、1 個には重み \(\phi = (\sqrt{5} - 1) / 2 \approx 0.618034\) が付いています。\(\phi\) は \(1 - \phi = \phi^{2}\) を満たすように選ばれています。Ford-Fulkerson のアルゴリズムがスタックすることを示すために、アルゴリズムが進行するにつれて三つの水平な辺の残余容量がどのように変化するかに注目します (他の 6 つの辺の残余容量は常に \(X - 1\) 以上です)。
Ford-Fulkerson のアルゴリズムが最初に上図の上部にある増加路を選んだとします。このとき三つの水平な辺の残余容量は左から順に 1, 0, \(\phi\) となります。ある整数 \(k\) に対して三つの水平な辺の残余容量が \(\phi^{k-1}\), \(0\), \(\phi^{k}\) であると帰納的に仮定すると、このとき
-
増加路 \(B\) に沿ってフローを \(\phi^{k}\) だけ増加させると、残余容量は \(\phi^{k+1}\), \(\phi^{k}\), \(0\) となる。
-
続いて増加路 \(C\) に沿ってフローを \(\phi^{k}\) だけ増加させると、残余容量は \(\phi^{k+1}\), \(0\), \(\phi^{k}\) となる。
-
続いて増加路 \(B\) に沿ってフローを \(\phi^{k+1}\) だけ増加させると、残余容量は \(0\), \(\phi^{k+1}\), \(\phi^{k+2}\) となる。
-
続いて増加路 \(A\) に沿ってフローを \(\phi^{k+1}\) だけ増加させると、残余容量は \(\phi^{k+1}\), \(0\), \(\phi^{k+2}\) となる。
が成り立ちます。よって帰納法により、\(4n + 1\) 回の増加ステップの後には残余容量が \(\phi^{2n-2}\), \(0\), \(\phi^{2n-1}\) となることが分かります。増加の回数を無限大にすると、フローの値は \[ 1 + 2 \sum_{i=1}^{\infty} \phi^{i} = 1 + \frac{2}{1 - \phi} = 4 + \sqrt{5} < 7 \] に収束します。しかし最大フローの値は明らかに \(2X + 1 \gg 7\) です。
実際の実装を考える読者は、なぜそもそも無理数の容量なんてものを考えるのかと不思議に思うかもしれません。コンピューターが正確に表現できるのは (小さな) 整数と (小さい、二進の) 分数だけなのにどうして、と。いい質問です! この質問に対する数学者の答えは「容量の整数への制限は文字通り人工的だから」です。容量が整数にしかならないというのはコンピューターのハードウェア (あるいはハードウェアに関連する物理法則) が作り出した人為的な制限であって、抽象的な計算問題が持つ本質的な特徴ではありません。より実際的な理由としては、無理数の入力に対するアルゴリズムの振る舞いを見ることで、浮動小数点数を含んだ入力に対する最悪ケースにおける振る舞いが分かるからというのがあります ――つまり、ひどいのです。常識的な容量を持つインスタンスであっても、よく考えずに Ford-Fulkerson のアルゴリズムを実装すると、浮動小数の切り捨て誤差だけが原因で無限ループに入ってしかも正しい答えに近づかないことがあります。
フローの合成と分解
フローの定義は頂点における保存条件が満たされるグラフの辺を入力とする関数であるのが普通ですが、他の定式化もあります。この定式化の方がより自然で有用なこともあります。
任意のグラフ \(G\) とソース頂点 \(s\) とシンク頂点 \(t\) が与えられたとして、\(G\) の適当な \((s,t)\)-フロー \(f, g\) と実数 \(\alpha, \beta\) を取り、次の関数 \(h: E \rightarrow \mathbb{R}\) を考えます: \[ h(u \rightarrow v) := \alpha \cdot f(u \rightarrow v) + \beta \cdot g(u \rightarrow v) \] ここで \(u \rightarrow v\) は任意の辺です。この定義は単純に \(h = \alpha f + \beta g\) とも書けます。定義を追っていくと、\(h\) もまた \((s,t)\)-フローでありその値は \(|h| = \alpha |f| + \beta |g|\) であることが分かります。これをより一般的に言うと、\((s,t)\)-フローの線形結合は \((s,t)\)-フローだということです。
よって任意の \((s,t)\)-フローは特殊な構造を持つフローの重み付き和として表現できます。\(s\) から \(t\) への任意の有向路 \(P\) について、対応する路フロー (path flow) を次のように定義します: \[ P(u \rightarrow v) = \begin{cases} 1 & \text{if } u \rightarrow v \in P \\ -1 & \text{if } v \rightarrow u \in P \\ 0 & \text{それ以外} \end{cases} \] 定義を追っていくと \(P: E \rightarrow \mathbb{R}\) は値が \(1\) の \((s, t)\) フローであることが簡単に示せます。ここでは路に流す一単位のフローとその路の両方を意図的に同じ記号 \(P\) で表しています。
同様に、任意の閉路 \(C\) に対応する閉路フロー (cycle flow) を次のように定義します: \[ C(u \rightarrow v) = \begin{cases} 1 & \text{if } u \rightarrow v \in C \\ -1 & \text{if } v \rightarrow u \in C \\ 0 & \text{それ以外} \end{cases} \] ここでも \(C: E \rightarrow \mathbb{R}\) が値の \(0\) の \((s, t)\) フローであることは簡単に示せます。
前述の議論から任意の路フローと閉路フローの線形結合もまたフローとなることが証明でき、この線形和をフロー分解 (flow decomposition) と呼びます。さらに、任意の非負フローには次の構造を持つフロー分解が存在します:
フロー分解定理 (Flow Decomposition Theorem) 全ての非負 \((s,t)\)-フローは有向 \((s,t)\)-路と有向閉路の正の線形和として書ける。そのとき有向辺 \(u \rightarrow v\) が分解の路または閉路に現れるのは \(f(u \rightarrow v) > 0\) のときに限られ、分解に含まれる路と閉路の数は \(f(e) > 0\) を満たす辺 \(e\) の数以下である。
証明 \(f\) に含まれるゼロでないフローを持つ辺の数に関する帰納法で示す。直感的に言うと、Ford-Fulkerson のアルゴリズムを逆回しにしたのがこの証明である。
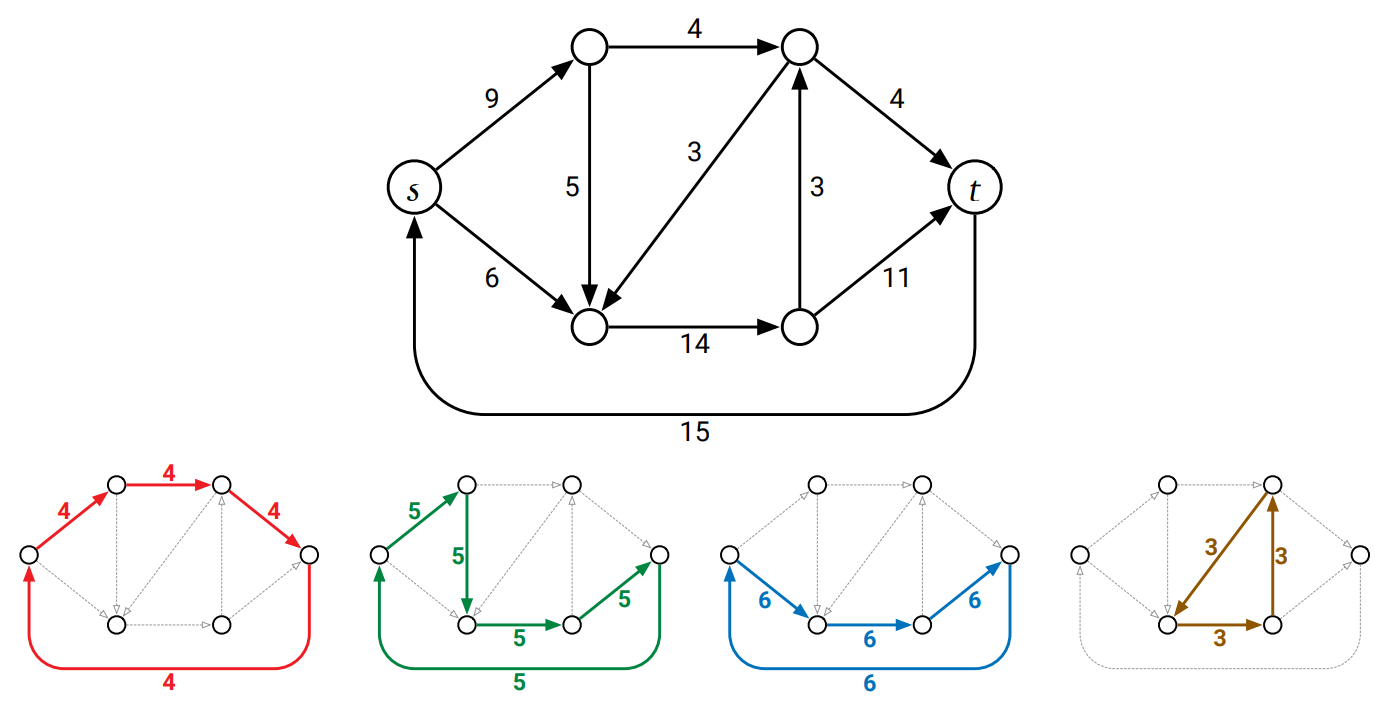
\(f\) において少なくとも一つの辺が正のフローを持っているならば、その辺を通る \((s,t)\)-路あるいは負閉路が存在する。よってその路または閉路を \(f\) から引けるだけ引くことで少なくとも一つの辺を \(f\) から消すことができる。こうするとゼロでないフローを持つ辺の数が減るので、あとは再帰の妖精が残りの分解をしてくれる。
この議論をきちんと行うために、 \(f\) が循環 (circulation) である特殊ケースを考える。フローが循環であるとは、値が \(0\) で \(s,t\) を含む全ての頂点において保存条件が成り立つことを言う。任意のフローネットワークとそれに含まれる循環 \(f\) を固定し、\(f(u \rightarrow v) > 0\) を満たす辺 \(u \rightarrow v\) の数を \(\#f\) とする。\(f\) が最大でも \(\max \lbrace 0, \# f - 1 \rbrace\) 個の閉路の正の線形結合に分解できることを、これから \(\# f\) に関する帰納法で示す。考えるべきケースは三つある:
-
\(\# f = 0\) の場合、\(f\) はゼロ個の閉路の線形結合である。
-
\(f (u \rightarrow v) > 0\) である辺 \(u \rightarrow v\) 全体が有向閉路を作る場合、\(f\) は一つの閉路の線形結合として表せる。
-
そうでない場合、\(f(u \rightarrow v) > 0\) である辺 \(u \rightarrow v\) について、任意の歩道 \(u = v_{0} \rightarrow\) \(v = v_{1} \rightarrow\) \(v_{2} \rightarrow \cdots \) であって全ての添え字 \(i\) について \(f(v_{i-1} \rightarrow v_{i} ) > 0\) であるものを考える。フローの保存条件から全ての頂点に出るフローと入るフローがあるので、この歩道は任意に長くできる。そうした場合二回以上訪れる頂点が存在するので、そのような頂点で一番添え字が若いものを \(v_{j} = v_{k}\) \((j < k)\) とする。このとき \(v_{j} \rightarrow v_{j-1} \rightarrow \cdots \rightarrow v_{k}\) は単純閉路 \(C\) となる。
\(\displaystyle F := \min_{e \in C} f(e)\) とし、新しい関数 \(f^{\prime}\) を \(f^{\prime} := f - F \cdot C\)、省略せずに書くと \[ f^{\prime}(u \rightarrow v) := \begin{cases} f(u \rightarrow v) - F & \text{if } u \rightarrow v \in C \\ f(u \rightarrow v) & \text{それ以外} \end{cases} \] と定義する。定義を追っていくと \(f^{\prime}\) は値が \(0\) で実現可能な \(G\) の循環であることが分かる。\(F\) の定義よりある \(e \in C\) において \(f(e) = F\) となるので、その \(e\) に対して \(f^{\prime}(e) = 0\) であり、したがって \(\# f^{\prime} \leq \# f - 1\) である。\(f^{\prime}\) は \(f\) より少ない辺しか持たないことから、帰納法の仮定より \(f^{\prime}\) には \(\# f^{\prime} - 1 \leq \# f - 2\) 個以下の閉路を使った分解が存在する。よってこの分解に \(C\) に沿って \(F\) だけフローを流したフローを追加すれば、\(\# f - 1\) 個の路または閉路を使った \(f\) の分解が手に入る。このことを簡潔に書けば \(f = f^{\prime} + F \cdot C\) である。
以上より \(f\) が最大でも \(\max \lbrace 0, \# f - 1 \rbrace\) 個の閉路の正の線形結合に分解できることが示せた。
\(f\) を任意のフローネットワークに対する \(|f| > 0\) を満たす任意の \((s,t)\)-フローとする。ネットワークに \(t \rightarrow s\) という辺を追加し、新しい循環 \(f^{\prime}\) を \(f^{\prime} (t \rightarrow s) = |f|\) およびそれ以外の辺に対しては \(f^{\prime} (u \rightarrow v) = f(u \rightarrow v)\) として定義する。ここで \(\# f^{\prime} = \# f + 1 \geq 2\) である。前述の議論より \(f^{\prime}\) は最大でも \(\#f^{\prime} - 1\) 個の有向閉路の正の線形結合に分解できる。この分解から辺 \(t \rightarrow s\) を取り除いたときに得られるのはフロー \(f\) に対する分解であり、最大でも \(\# f^{\prime} - 1 \leq \# f\) 個の \((s,t)\)-路および閉路しか持たない。具体的には、\(f^{\prime}\) における \(s \rightarrow t\) を含む閉路は \(f\) における \((s,t)\)-路となり、\(f^{\prime}\) における \(s \rightarrow t\) 閉路を含まない閉路は \(f\) においても閉路のままとなる。 \(\Box\)
フロー分解定理の証明から、次の特殊な場合に対する強い結果が得られます:
- 任意の循環は閉路の重み付き和に分解できる。路は必要ない。
- 任意の非巡回 \((s,t)\)-フローは \((s,t)\)-路の重み付き和に分解できる。閉路は必要ない。
さらに、任意のフローから閉路を削除すると同じ値を持つ非巡回フローが手に入ることも分かります。つまり全てのフローネットワークには最大非巡回 \((s,t)\)-フローが存在します。
この証明は \((s,t)\)-フローを路と閉路に分解するアルゴリズムとしても読むことができます。つまり \((s,t)\)-路または有向閉路を現在のフローから見つけてそれをできる限り取り除くという処理をフローが空になるまで繰り返すアルゴリズムであり、 Ford-Fulkerson のアルゴリズムに似ています。次のようにすれば路フローまたは閉路フローを \(O(V)\) 時間で見つけられます:
-
\(s\) から出る辺に正のフローを持つものがあるなら、\(s\) から始めて \(t\) に到達する (路フローが手に入る) か同じ頂点に二度到達する (閉路フローが手に入る) まで任意の辺をたどる。
-
\(s\) から出る辺に正のフローを持つものが無いなら、正のフローを持つ辺の始点となっている頂点 \(v\) を見つけて \(v\) から始めて同じ頂点に二度到達する (閉路フローが手に入る) まで任意の辺をたどる。
両方の場合においてアルゴリズムがスタックしないことは保存条件から分かります。各反復は \(O(V)\) 時間で行うことができ、フローを引くという処理で少なくとも一つの辺がフローから消えるので、フロー分解アルゴリズム全体の実行時間は \(\pmb{O(VE)}\) です。
フロー分解定理を使うと、路または閉路を一つずつ作る処理を反復する任意の最大フローアルゴリズムの実行時間の下界が分かります。全てのフローは最大でも \(E\) 個の路と閉路に分解でき、それぞれの路と閉路は最大でも \(V\) 個の辺を持つことから、フロー分解全体の複雑性は \(O(VE)\) です。さらに任意のフロー分解が \(\Theta(VE)\) の複雑性を持つフローは簡単に構築できるので、各反復ごとに一つの路または閉路を実際に構築する最大フローアルゴリズム ――具体的には、Ford と Fulkerson の増加路アルゴリズムの全ての実装―― は最悪ケースにおける実行時間が \(\Theta(VE)\) となります。
Edmonds と Karp のアルゴリズム
Ford と Fulkerson のアルゴリズムは残余グラフのどの路を増加させるかを指定しません。このアルゴリズムの最悪計算時間がひどいのは、増加路の選び方をいくらでも悪くできるのが原因です。1970 年代前半、Jack Edmonds (ジャック・エドモンズ) と Richard Karp (リチャード・カープ) は増加路を選ぶための二つの自然な方法を解析し、どちらを使った場合でもより効率の良いアルゴリズムが得られることを示しました。
最幅増加路
Edmonds と Karp が解析した一つ目の規則を次に示します。この規則を使ったアルゴリズムは本質的に貪欲アルゴリズムとなります:
ボトルネックの値が一番大きい増加路を選ぶ。
Jarník の最小全域木アルゴリズムまたは Dijkstra のアルゴリズムに似た "最良優先探索" アルゴリズムを使えば、有向グラフの最大ボトルネック \((s,t)\)-路を \(O(E \log V)\) 時間で計算できます。このアルゴリズムは \(T = \lbrace s \rbrace\) から始めて \(T\) から伸びる容量の一番大きい辺を \(T\) に加えていくことで \(s\) を根とする有向木 \(T\) を成長させ、\(T\) に \(t\) が追加されたらその時点で終了するというものです。あるいは Kruskal のアルゴリズムに似たもの ――容量の降順に辺を木に追加していき、\(s\) から \(t\) への路が完成するまで続ける―― を使っても同じ処理はできますが、グラフが有向である場合にはこのアプローチは低速になります。
フローアルゴリズムの実行時間解析を完了させるには、アルゴリズムが停止するまでの反復回数の上限が必要です。実は、容量が実数だとこのアルゴリズムが停止しない場合があります (練習問題 10.19 で扱います)。しかし容量が整数なら、実行時間は最大フローの値 \(|f^{\ast}|\) を使うことで次のように解析できます。
\(f\) を \(G\) の任意のフローとし、\(f^{\prime}\) を現在の残余グラフ \(G_{f}\) における最大フローとします (例えばアルゴリズムが始まった時点では \(G_{f} = G\) および \(f^{\prime} = f^{\ast}\) です)。前に示した \(f^{\prime}\) が最大 \(E\) 個の路と閉路に分解できるという事実と平均値を使った簡単な議論から、この分解に含まれる少なくとも一つの路には \(|f^{\prime}| / E\) 以上のフローが流れることが分かります。よって \(G_{f}\) に含まれる最も幅の大きい \((s,t)\)-路は \(|f^{\prime}| / E\) 以上の幅を持ちます。
したがって \(G_{f}\) に含まれる最大ボトルネック路で \(f\) を増加させると、残余グラフ \(G_{f}\) の最大フローの値は \(1 - 1/E\) 倍以下になります。これを言い換えると、残余最大フローの値は反復回数に対して指数的に小さくなるということです。\(E \cdot \ln |f^{\ast}|\) 回の反復の後、\(G_{f}\) に含まれる最大フローの値は \[ |f^{\ast}| \cdot (1 - 1/E)^{E \cdot \ln |f^{\ast}|} < |f^{\ast}| e^{-\ln |f^{\ast}|} = 1 \] を満たすので (この \(e\) は Euler の定数です。ごめんなさい)、\(E \cdot |f^{\ast}|\) 回の反復によって残余最大フローの値は \(1\) より小さくなります。もし容量が整数ならば残余最大フローの値も整数となるので、この値は \(0\) 、すなわち \(f\) は最大フローです!
まとめると、整数の容量を持つグラフに対する Edmonds-Karp の "最幅路" アルゴリズムの実行時間は \(\pmb{O(E^{2} \log E \log |f^{\ast}|)}\) となります。何も工夫をしない Ford-Fulkerson の最悪実行時間と違って、このアルゴリズムの実行時間は入力サイズの多項式で抑えられます。
Ford-Fulkerson のアルゴリズムと同じように、この "最幅路" アルゴリズムに任意の実数の容量を持つネットワークを入力すると無限ループになってスタックすることがあります。しかしここで述べた解析から、アルゴリズムが止まらない場合でもフロー \(f\) が極限において最大フローに限りなく近づくことが分かります。
最短増加路
Edmonds と Karp が解析した二つ目の規則を次に示します。この規則は Ford と Fulkerson が最大フローアルゴリズムを示した論文においても実用上のヒューリスティックとして提案されていました。またロシア人数学者 Yefim Dinitz (イェフィム・ディニッツ) も同じ規則に対する考察を Edmonds と Karp とは独立に 1979 年に発表しています4。
辺の数が最小の増加路を選ぶ。
残余グラフに含まれる最短の増加路は幅優先探索によって \(O(E)\) 時間で見つけられます。意外にも、この規則を使ったアルゴリズムは辺の容量の値に関係なく多項式回の反復の後に停止します!
\(f_{i}\) を \(i\) 回の増加ステップの後のフローとし、\(G_{i}\) を \(f_{i}\) に対応する残余グラフとします。例えば \(f_{0}\) は全てがゼロのフローであり、\(G_{0} = G\) です。全ての頂点 \(v\) に対して、\(G_{i}\) における \(s\) から \(v\) への重み無し最短路の長さを \(\pmb{level_{i}(v)}\) とします。同じことですが、\(level_{i}(v)\) を \(s\) を根とする \(G_{i}\) の幅優先探索木における \(v\) の「高さ (level)」と定義することもできます。\(G_{i}\) において \(s\) から \(v\) への路が無い場合には \(level_{i}(v) = \infty\) となります (\(\min \varnothing = \infty\) だからです)。アルゴリズムの多項式上界の証明は残余グラフの変化に関する二つの観察を利用します。
一つ目の観察は \(level\) の非減少性です。
命題 10.2 全ての頂点 \(v\) と整数 \(i > 0\) について \(level_{i}(v) \geq level_{i-1}(v)\)。
証明 \(i > 0\) を任意の整数、\(v\) を適当な頂点とする。\(level_{i}(v)\) に対する帰納法で示す (\(i\) に対する帰納法ではない)。帰納法の仮定から、\(level_{i} (u) < level_{i} (v)\) を満たす任意の頂点 \(u\) について \(level_{i} (u) \geq level_{i-1} (u)\) が成り立つ。\(v\) について考えるべきケースは三つある:
-
\(v = s\) の場合、 \(level_{i}(s) = 0 \geq 0 = level_{i-1}(s)\) となって成り立つ。
-
\(G_{i}\) に \(s\) から \(v\) への路が無い場合、\(level_{i} (v) = \infty \geq level_{i-1}(v)\) となって成り立つ。
-
それ以外の場合、\(G_{i}\) における \(s\) から \(v\) への任意の最短路を \(s \rightarrow\) \(\cdots \rightarrow\) \(u \rightarrow v\) とする。この路が最短路であることから \(level_{i}(v) = level_{i}(u) + 1\) であり、帰納法の仮定から \(level_{i} (u) \geq level_{i-1} (u)\) なので、\(level_{i-1}(u) \geq level_{i-1}(v) - 1\) を示せばよい。\(u \rightarrow v\) について考えるべきケースがさらに二つある。
-
\(G_{i-1}\) において \(u \rightarrow v\) が辺の場合、\(level_{i-1}(\cdot)\) は幅優先探索によって定義されることから \(level_{i-1}(v) \leq level_{i-1} (u) + 1\) が成り立つ。
-
そうでなくて \(u \rightarrow v\) が \(G_{i-1}\) において辺でない場合、その逆 \(v \rightarrow u\) は \(i\) 番目の増加路に含まれる。今考えている規則からこの増加路は \(G_{i-1}\) における \(s\) から \(t\) への最短路だから、\(level_{i-1} (v) = \) \(level_{i-1} (u) {\color{red}{}-{}} 1 \leq \) \(level_{i-1} (u) {\color{red}{}+{}} 1\) が分かる。
-
よっていずれの場合でも \(level_{i} (v) = \) \(level_{i} (u) + 1 \geq \) \(level_{i-1} (u) + 1 \geq \) \(level_{i-1}(v)\) が成り立つ。 \(\Box\)
この証明で重要なのは、フローを追加すると増加路のボトルネック辺が残余グラフから消失し、増加路に含まれる辺のいくつかはその逆が残余グラフに (再び) 出現するという事実です。二つ目の観察はこの消失と出現の回数の上界に関するものです。
命題 10.3 Edmonds-Karp の最短増加路アルゴリズムにおいて、任意の辺 \(u \rightarrow v\) は最大でも \(V/2\) 回しか \(G_{f}\) から消失しない。
証明 \(u \rightarrow v\) が二つの残余グラフ \(G_{i}\) と \(G_{j+1}\) \((i < j)\) に現れ、その間の残余グラフ \(G_{i+1},\ldots, G_{j}\) には表れないとする。このとき \(u \rightarrow v\) が \(i\) 番目の増加路に含まれることから \(level_{i} (v) = level_{i} (u) + 1\) であり、\(v \rightarrow u\) が \(j\) 番目の増加路に含まれることから \(level_{j}(v) = level_{j}(u) - 1\) である。これと 命題 10.2 より \[ level_{j}(u) = level_{j} (v) + 1 \leq level_{i} (v) + 1 = level_{i} (u) + 2 \] つまり \(u \rightarrow v\) が消失してもう一度出現すると、\(s\) から \(u\) への距離は少なくとも 2 増える。全ての頂点 \(v\) に対して \(level_{i} (v)\) は \(V\) より小さいかそうでなければ無限大なので、消失の回数は最大でも \(V/ 2\) 回である。 \(\Box\)
以上の観察から反復の回数の上界を求められます。全ての辺は最大でも \(V/2\) 回消失することから、全ての辺の消失の回数は \(EV/2\) 回以下です。一度の反復で消失することが保証されている辺は一本だけなので、このアルゴリズムは停止するまでに最大 \(EV/2\) 回だけ反復します。各反復には \(O(E)\) 時間がかかることから、アルゴリズム全体の実行時間は \(\pmb{O(VE^{2})}\) です。
さらなる進展
最大フローアルゴリズムの物語はこれで終わりでは決してありません。何十年にも渡る高速なアルゴリズムの研究の成果を次の表にまとめます5。ここにあるアルゴリズムは全て反復によって最大フローを計算するものであり、ほとんどのアルゴリズムには二つのバージョンがあります: 一つは各反復で総当たりを使う単純なバージョンで、もう一つは洗練されたデータ構造を使ってフローネットワークの全域木を管理することで反復と全域木の更新を対数時間で行うバージョンです。これまでに知られている最速のアルゴリズムが最適であると思ってはいけません。最大フローは現在でも活発に研究が行われている領域です。
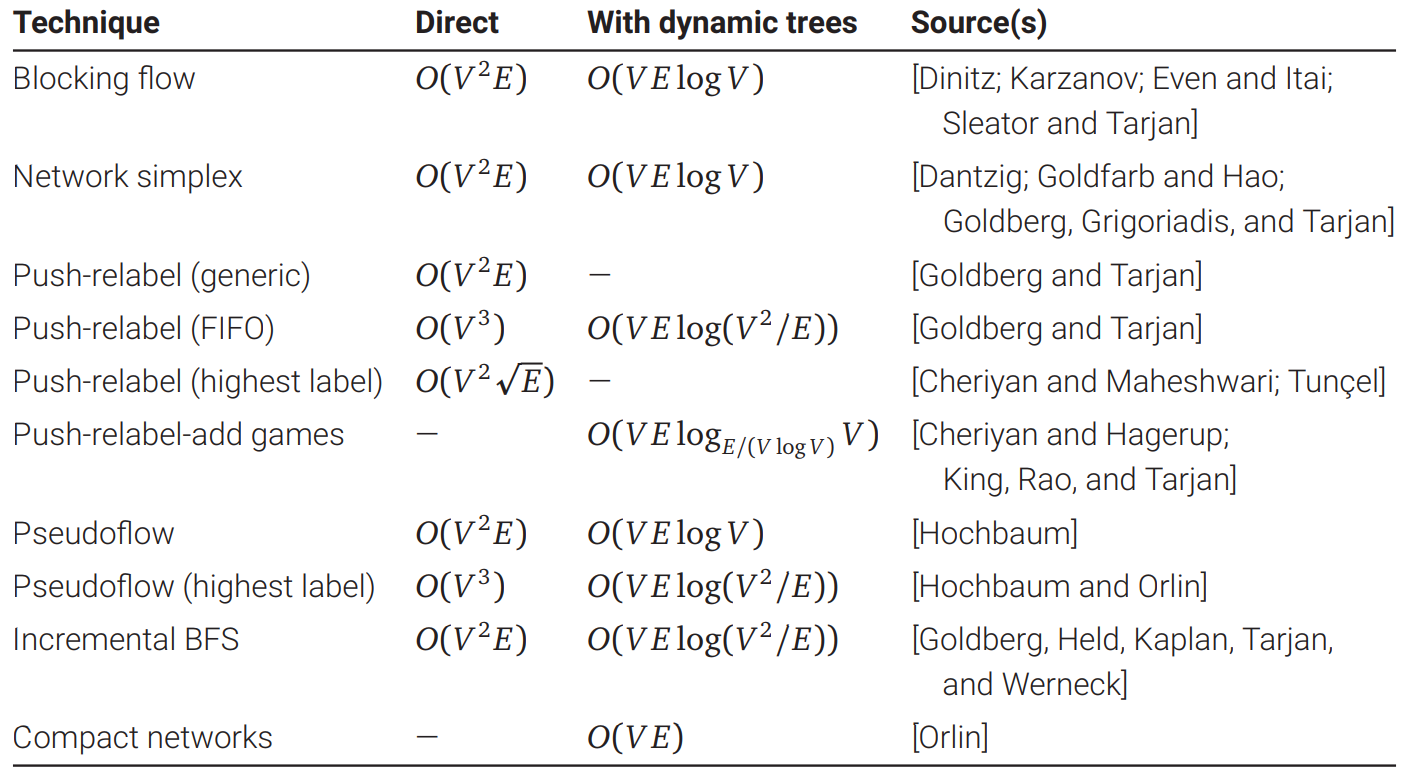
現在知られている (purely combinatorial な) 最速の最大フローアルゴリズムは、2012 年に James Orlin (ジェームス・オーリン) によって発表されたものです。実行時間は \(\pmb{O(VE)}\) であり、フロー分解の最悪計算時間と同じです。このアルゴリズムはそれまでに発見されたアルゴリズムやデータ構造をブラックボックスとして使っており、それらのほとんどがとても複雑なので、Orlin のアルゴリズムの詳細はこの本の範囲を大きく超えます。また Orlin のアルゴリズムを拡張すると、具体的なフロー分解を構築しないアルゴリズムが得られます。実際このアルゴリズムは \(O(V)\) 個しか辺を持たないグラフに対しては実行時間が \(O(V^{2} / \log V)\) となります!
しかしもちろん、最大フローアルゴリズムを使うアルゴリズムの解析においては、この実行時間の上界を使って構いません。次の文章をチートシートに書いておいて宿題で使いましょう:
最後に、全ての辺の容量が \(1\) であるような "単位容量" ネットワークに対するさらに高速な最大フローアルゴリズムを紹介します。1973 年、Alexander Karzanov (アレキサンダー・カルザノフ) は Dinitz (ディニッツ) の blocking-flow アルゴリズム ――上の表で一番上にあるもの―― が単位容量という条件の下では \(O(\min \lbrace V^{2 / 3}, E^{1 / 2} \rbrace E)\) 時間で実行されることを示しました (この実行時間はフロー分解に \(\Omega(VE)\) 時間かかるという事実と矛盾するように見えますが、Karzanov の解析からは単位容量のネットワークは \(O(\min \lbrace V^{2 / 3}, E^{1 / 2} \rbrace E)\) 時間で路に分解できることが分かります)。このアルゴリズムは 40 年以上にわたって単位容量のネットワークに対する最速の最大フローアルゴリズムでしたが、この記録は 2014 年 に Aleksander Mądry (アレクサンダー・モドリー) よって破られました。Mądry が示した真に驚くべきアルゴリズムの実行時間は \(O(E^{10/7} \text{polylog } E)\) です。ここでも Mądry のアルゴリズムの詳細はこの本の範囲を大きく超え、正直なところ著者の技量も追いついていません。
練習問題
-
有向グラフ \(G = (V, E)\) と二つの頂点 \(s, t\) と容量関数 \(c: E \rightarrow \mathbb{R}^{+}\) と \(f: E \rightarrow \mathbb{R}\) が与えられたとします。\(f\) が \(G\) の最大 \((s,t)\)-フローであるかを判定するアルゴリズムを説明してください。
-
フローネットワーク \(G\) の実現可能な \((s,t)\)-フローを二つ取って \(f, f^{\prime}\) \((|f^{\prime}| > |f|)\) とします。残余グラフ \(G_{f}\) に実現可能な \((s,t)\)-フローであって値が \(|f^{\prime}| - |f|\) であるものが存在することを示してください。
-
\(G\) を適当なフローネットワーク、\(u \rightarrow v\) を \(G\) の適当な辺とします。最小 \((s,t)\)-カット \((S, T)\) であって \(u \in S\) かつ \(v \in T\) となるものが存在するならば、最小カット \((S^{\prime}, T^{\prime})\) であって \(u \in T^{\prime}\) かつ \(v \in S^{\prime}\) となるものは存在しないことを証明してください。
-
\((S, T)\) と \((S^{\prime}, T^{\prime})\) が適当なフローネットワーク \(G\) の最小 \((s,t)\)-カットであるとき、\((S \cap S^{\prime}, T \cup T^{\prime})\) と \((S \cup S^{\prime}, T \cap T^{\prime})\) も \(G\) の最小 \((s,t)\)-カットであることを証明してください。
-
フローネットワーク \(G\) に逆向きの辺の組 \(u \rightarrow v\) と \(v \rightarrow u\) が両方含まれ、どちらも正の容量を持つとします。この二つの辺の容量を \(\min \lbrace c(u \rightarrow v), c(v \rightarrow u) \rbrace\) だけ減少させたフローネットワークを \(G^{\prime}\) とします。つまり \(G\) に対して次の操作を行って得られるグラフが \(G^{\prime}\) です:
-
\(c(u \rightarrow v) > c (v \rightarrow u)\) ならば、 \(u \rightarrow v\) の容量を \(c(u \rightarrow v) - c(v \rightarrow u)\) として \(v \rightarrow u\) を削除する。
-
\(c(u \rightarrow v) < c (v \rightarrow u)\) ならば、 \(v \rightarrow u\) の容量を \(c(v \rightarrow u) - c(u \rightarrow v)\) として \(u \rightarrow v\) を削除する。
-
\(c(u \rightarrow v) = c(v \rightarrow u)\) ならば、\(u \rightarrow v\) と \(v \rightarrow u\) の両方を削除する。
-
\(G^{\prime}\) における最大 \((s,t)\)-フローは全て \(G\) における最大 \((s,t)\)-フローでもあることを証明してください (このことから、\(G\) に含まれる逆向きの辺の組を全て削除して得られるフローネットワークが、\(G\) と同じ最大フローを持つ逆向きの辺の組を持たないグラフであることが言えます)。
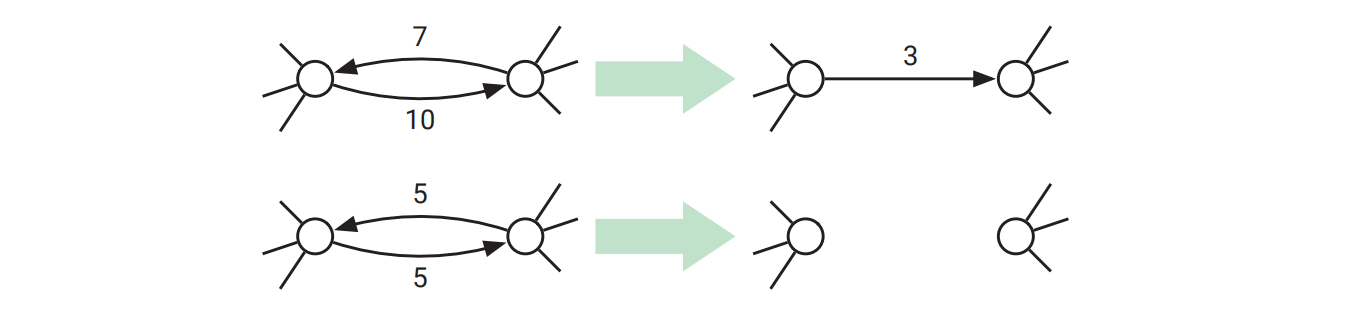 図 10.11辺が一方向にしかないという仮定を強制する
図 10.11辺が一方向にしかないという仮定を強制する -
\(G^{\prime}\) における最小 \((s,t)\)-カットは全て \(G\) における最小 \((s,t)\)-カットでもあること、およびその逆を証明してください。
-
\(G\) における最大 \((s,t)\)-フローであって \(G^{\prime}\) における最大 \((s,t)\)-フローでないものが少なくとも一つ存在することを示してください。
-
-
-
与えられたフローネットワークが唯一の最大 \((s,t)\)-フローを持つかどうかを判定する効率の良いアルゴリズムを説明してください。
-
与えられたフローネットワークが唯一の最小 \((s,t)\)-カットを持つかどうかを判定する効率の良いアルゴリズムを説明してください。
-
唯一の最大 \((s,t)\)-フローと複数の最小 \((s,t)\)-カットを持つフローネットワークを示してください。
-
複数の最大 \((s,t)\)-フローと唯一の最小 \((s,t)\)-カットを持つフローネットワークを示してください。
-
-
ネットワーク \(G\) の \((s,t)\)-フローが非巡回 (acyclic) であるとは、正のフローを持つ辺からなる有向閉路が存在しないことを言います。つまり、正のフローを持つ辺からなる部分グラフが DAG ならばそのフローは非巡回です。
-
非巡回最大 \((s,t)\)-フローを計算するアルゴリズムを説明、解析してください。アルゴリズムの実行時間は漸近的に Ford-Fulkerson のアルゴリズムと同じであるべきです。
-
全ての \((s,t)\)-フローが非巡回であるかどうかを判定するアルゴリズムを説明、解析してください。
-
-
\(G=(V,E)\) を辺の容量が全て \(1\) であるフローネットワークとし、\(s\) から \(t\) への最短路の長さが \(d\) 以下とします。
-
最大 \((s,t)\)-フローの値が \(E/d\) 以下であることを示してください。
-
\(G\) が単純である、つまり任意の頂点 \(u\) と \(v\) の間には最大でも一つの辺しかないと仮定します (定義上はフローネットワークに平行辺が含まれていても構わないことに注意してください)。最大 \((s, t)\) -フローの値が \(O(V^{2}/d^{2})\) 以下であることを示してください。 [ヒント: 根が \(s\) である BFS 木において、平均の高さにある頂点はいくつですか?]
-
-
辺の容量が全て \(1\) であるフローネットワーク \(G=(V,E)\) と整数 \(k\) が与えられたとします。\(G\) から \(k\) 本の辺を削除してグラフに含まれる最大 \((s,t)\)-フローの値を最小にしたいときに、削除すべき \(k\) 本の辺を特定するアルゴリズムを説明、解析してください。
-
フロー分解定理 の証明で行った解析はもっと厳密に行うことができます。 \(G = (V, E)\) を任意のフローネットワーク、\(f\) を \(G\) に含まれる任意の \((s,t)\)-フローとします。
-
\(|f| = 0\) ならば \(f\) は最大でも \(E - V + 1\) 個の有向閉路の重み付き和であることを示してください。ただし和に現れる有向閉路に含まれる全ての辺 \(e\) は \(f(e) > 0\) を満たすとします。
-
\(|f| > 0\) ならば \(f\) は最大でも \(E - V + 2\) 個の有向路または有向閉路の重み付き和であることを示してください。ただし和に現れる路と有向閉路に含まれる全ての辺 \(e\) は \(f(e) > 0\) を満たすとします。
-
前問の上界が厳密であることを示してください。つまり \(E-V+1\) 個より少ない有向閉路で分解できない循環と \(E - V + 2\) 個より少ない有向路と有向閉路で分解できないフローを示してください。 [ヒント: この問題は簡単です。]
-
-
♣ 任意の \((s,t)\)-フローの線形結合もまた \((s,t)\)-フローであるという観察から、任意のグラフにおける (実現可能でないものを含む) 全ての \((s,t)\)-フローは実線形空間をなすことが分かります。この線形空間のことをグラフのフロー空間 (flow space) と言います。
-
任意の連結グラフ \(G=(V, E)\) のフロー空間の次元は \(E - V + 2\) であることを示してください。
-
\(T\) を \(G\) の任意の全域木とします。次の路と閉路の集合がフロー空間の基底となることを示してください。
-
\(T\) における \(s\) から \(t\) への (唯一の) 路。
-
全ての \(e \notin T\) に対する、\(T \cup \lbrace e \rbrace\) に含まれる (唯一の) 閉路。
-
-
\(T\) を \(G\) の任意の全域木、\(F\) を \(T\) の適当な辺を一つ削除して得られる森とします。次の路と閉路の集合がフロー空間の基底となることを示してください。
-
\(F\) の二つの成分を繋いでいる全ての \(e \notin F\) に対する、\(F \cup \lbrace e \rbrace\) に含まれる (唯一の) \(s\) から \(t\) への路。
-
\(F\) の同じ成分を繋いでいる全ての \(e \notin F\) に対する、\(F \cup \lbrace e \rbrace\) に含まれる (唯一の) 閉路。
-
-
次の主張を証明または反証してください: 「任意の連結フローネットワークには、\(s\) から \(t\) への単純路だけからなるフロー空間の基底が存在する」
-
-
カットが頂点の分割ではなくてグラフの辺の部分集合として定義されることもあります。この問題ではこの二つの定義がほぼ同値であることを示します。
有向辺の集合 \(X\) が \(s\) と \(t\) を分離するとは、\(s\) から \(t\) への任意の有向路が少なくとも一つの \(X\) の要素を含むことを言います。また任意の頂点集合 \(S\) について、\(S\) から出る辺の集合を \(\pmb{\delta S}\) で表すことにします。つまり \(\delta S :=\) \(\lbrace u \rightarrow v\ |\ u \in S, v \notin S \rbrace\) です。
-
\((S, T)\) が \((s,t)\)-カットならば \(\delta S\) が \(s\) と \(t\) を分離することを示してください。
-
\(s\) と \(t\) を分離する任意の辺集合を \(X\) とします。\((s,t)\)-カット \((S, T)\) であって \(\delta S \subseteq X\) を満たすものが存在することを示してください。
-
\(s\) と \(t\) を分離する最小の辺集合を \(X\) とします (このような辺集合を帯 (bond) と呼ぶこともあります)。\((s,t)\)-カット \((S, T)\) であって \(\delta S = X\) を満たすものが存在することを示してください。
-
-
ネットワークの各辺 \(u \rightarrow v\) に付いているのが容量ではなくて非負の需要 (demand) であるとします。このとき \((s,t)\)-フロー \(f\) が実現可能とは、任意の辺 \(u \rightarrow v\) に対して \(f(u \rightarrow v) \geq d(u \rightarrow v)\) であることを言います。この設定における問題として自然なのは、実現可能な \((s,t)\)-フローであって値が最小のものを考える問題です。
-
グラフと需要関数と \(s,t\) が与えられたときに、実現可能な最小 \((s,t)\)-フローを計算する効率の良いアルゴリズムを説明してください。 [ヒント: 全ての辺においてゼロでないフローを見つけ、実現可能になるまで大きくする。]
-
辺に容量の付いたグラフの最大フローを計算するサブルーチン \(\textsc{MaxFlow}\) を使えると仮定したときに、与えられたグラフと辺の需要に対する最小フローを計算する効率の良いアルゴリズムを説明してください。アルゴリズムが \(\textsc{MaxFlow}\) を使うのは一度だけとしてください。
-
需要という言葉を使って最大フロー最小カット定理に似たものを述べ、それを証明してください。(最小フローが最大カットと対応しますか?)
-
-
任意のフローネットワーク \(G\) と頂点 \(u, v\) について、\(u\) から \(v\) への任意の路に含まれる辺の最小容量の最大値を \(\mathit{bottleneck}_{G}(u, v)\) とします。
-
\(\mathit{bottleneck}_{G}(s, t)\) の値を \(O(E \log V)\) 時間で求めるアルゴリズムを説明、解析してください。この値は Edmonds-Karp の "最幅増加路" アルゴリズム の最初の反復において追加されるフローの値です。
-
\(G\) が無向である、あるいは全ての辺に対して \(c(u \rightarrow v) = c(v \rightarrow u)\) であるとします。\(\mathit{bottleneck}_{G}(u, v)\) を \(O(V + E)\) 時間で計算するアルゴリズムを説明、解析してください。有向グラフに対してこのアルゴリズムを適用できないのはどうしてですか? [ヒント: 辺容量の中央値を見つける。]
-
❤ フローネットワーク \(G\) が無向であると仮定します。\(G\) の全域木 \(T\) であって任意の頂点 \(u, v\) について \(\mathit{bottleneck}_{T} (u, v) = \mathit{bottleneck}_{G} (u,v)\) であるものを構築するアルゴリズムを説明、解析してください (\(T\) の辺の容量は \(G\) と同じです)。満点のためには、アルゴリズムの実行時間が \(O(E)\) 時間であることが求められます。
-
-
辺に整数の重みのついたフローネットワークを \(G\) とし、\(G\) の整数最大フローを \(f^{\ast}\) とします。次の操作に対するアルゴリズムを説明してください:
- \(\textsc{Increment}(e)\): 辺 \(e\) の容量を \(1\) 増やし、最大フローを更新する。
- \(\textsc{Decrement}(e)\): 辺 \(e\) の容量を \(1\) 減らし、最大フローを更新する。
二つのアルゴリズムは \(f^{\ast}\) を使って最大フロー(再)計算し、実行時間は最大フローを最初から計算するよりも短くあるべきです。
-
辺に整数の容量がついたネットワークを \(G\) とします。\(G\) の辺が upper-binding であるとは、その辺の容量を \(1\) 増やすと \(G\) の最大フローの値が増加することを言います。同様に \(G\) の辺が lower-binding であるとは、その辺の容量を減らすと \(G\) の最大フローの値が減少することを言います。
-
どんなネットワーク \(G\) にも upper-binding な辺が含まれますか? 答えが正しいことを証明してください。
-
どんなネットワーク \(G\) にも lower-binding な辺が含まれますか? 答えが正しいことを証明してください。
-
\(G\) に含まれる upper-binding な辺を全て見つけるアルゴリズムを説明してください。入力は \(G\) と \(G\) の最大フローで、実行時間は \(O(E)\) としてください。
-
\(G\) に含まれる lower-binding な辺を全て見つけるアルゴリズムを説明してください。入力は \(G\) と \(G\) の最大フローで、実行時間は \(O(EV)\) としてください。
-
-
与えられたフローネットワーク \(G\) が複数の最小 \((s,t)\)-カットを持つとします。最良の最小 \((s,t)\)-カット \((S, T)\) を、最小 \((s,t)\)-カットの中で \(S\) から \(T\) に向かう辺の数が最小なものとして定義します。
-
辺の容量が整数のときに、最良の最小 \((s,t)\)-カットを見つける効率の良いアルゴリズムを説明してください。
-
辺の容量が任意の実数のときに、最良の最小 \((s,t)\)-カットを見つける効率の良いアルゴリズムを説明してください。
-
与えられたネットワークの最良の最小 \((s,t)\)-カットが唯一であるかどうかを判定する効率の良いアルゴリズムを説明してください。
-
-
最大フローを初めて教えることになった新米の助教授は、Ford-Fulkerson の一般的な増加路アルゴリズムを "貪欲に" した次のアルゴリズムを生徒に示しました。このアルゴリズムを使えば残余グラフを作る代わりに増加路に沿って辺の容量を減らすだけ6で済みます! 辺を飽和させるときにはただグラフから取り除けばいいのです。残余グラフとかいう、わけの分からないものなんて考えなくていいでしょう?
procedure \(\texttt{GreedyFlow}\)(\(G,c,s,t\))
for \(G\) の辺 \(e\) do
\(f(e) \leftarrow 0\)
while \(G\) に \(s\) から \(t\) への路がある do
\(\pi \leftarrow s\) から \(t\) への適当な路
\(F \leftarrow \pi\) に含まれる容量が最小の辺
for \(e \in \pi\) do
\(f(e) \leftarrow f(e) + F\)
if \(c(e) = F\) then
\(e\) を \(G\) から削除する
else
\(c(e) \leftarrow c(e) - F\)
-
\(\textsc{GreedyFlow}\) が常に最大フローを計算するわけではないことを示してください。
-
\(\textsc{GreedyFlow}\) が最大フローの良い近似を計算することさえ保証されていないことを示してください。つまり、任意の \(\alpha > 1\) についてあるフローネットワーク \(G\) が存在して、\(G\) の最大フローの値が \(\textsc{GreedyFlow}\) の計算するフローの値の \(\alpha\) 倍よりも大きくなることを示してください。 [ヒント: \(\textsc{GreedyFlow}\) の各反復において最悪の路 \(\pi\) が選ばれると仮定してください。]
-
-
Maurice Queyranne (モーリス・クイラン) は 1980 年、Edmonds と Karp の"最幅路" ヒューリスティックが停止しないようなネットワークの例を発表しました。オリジナルの Ford-Fulkerson のアルゴリズムに対する Zwick の例 と同じように、この例でも \(\phi = (\sqrt{5} - 1) / 2\) が使われます。下図における三つの垂直な辺が Zwick の例における三つの水平な線と本質的に同じ役目を果たします。
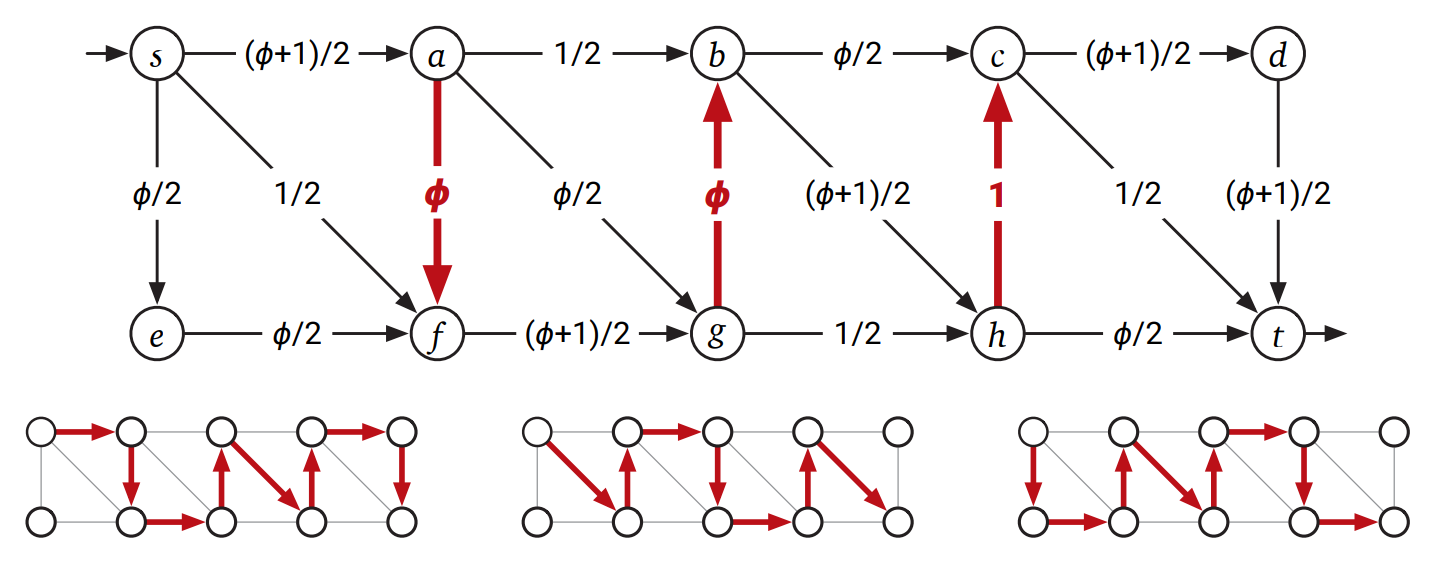 図 10.12Queyranne のネットワークとその「最幅」増加路
図 10.12Queyranne のネットワークとその「最幅」増加路-
次の操作の無限列が Edmonds-Karp の "最幅路" アルゴリズムの実行したときの操作列として正しいことを示してください (図の下部も参照)。
procedure \(\texttt{QueyranneFatPaths}\)()
for \(i \leftarrow 1\) to \(\infty\) do
\(\phi^{3i-2}\) のフローを \(s \rightarrow a \rightarrow f \rightarrow g \rightarrow b \rightarrow h \rightarrow c \rightarrow d \rightarrow t\) に流す
\(\phi^{3i-1}\) のフローを \(s \rightarrow f \rightarrow a \rightarrow b \rightarrow g \rightarrow h \rightarrow c \rightarrow t\) に流す
\(\phi^{3i}\) のフローを \(s \rightarrow e \rightarrow f \rightarrow a \rightarrow g \rightarrow b \rightarrow c \rightarrow h \rightarrow t\) に流す
-
Queyranne のネットワークにおいて最大フローを出力する \(O(1)\) 個の増加路の列を示してください。
-
-
❤ \(\pmb{(s, t)}\)-直列-並列グラフ とは、特別な二つの頂点 \(s,t\) を持つ有向非巡回グラフであって次の条件のうちどれかを満たすものを言います:
-
ベースケース: \(s\) から \(t\) への有向辺だけからなるグラフ。
-
直列: \((s,u)\)-直列-並列グラフと \((u,t)\)-直列-並列グラフの和集合。ただし二つのグラフに共通する頂点は \(u\) だけ。
-
並列: 二つの \((s,t)\)-直列-並列グラフの和集合。ただし二つのグラフに共通する頂点は \(s\) と \(t\) だけ。
任意の \((s,t)\)-直列-並列グラフ \(G\) は分解木 (decomposition tree) を使って表すことができます。分解木の頂点には三つの種類があり、それぞれ (\(G\) の辺を表す) 葉と (\(s\) と \(t\) 以外の頂点を表す) 直列頂点および並列頂点です。一つの直列-並列グラフに複数の分解木が存在することがあり得ます。
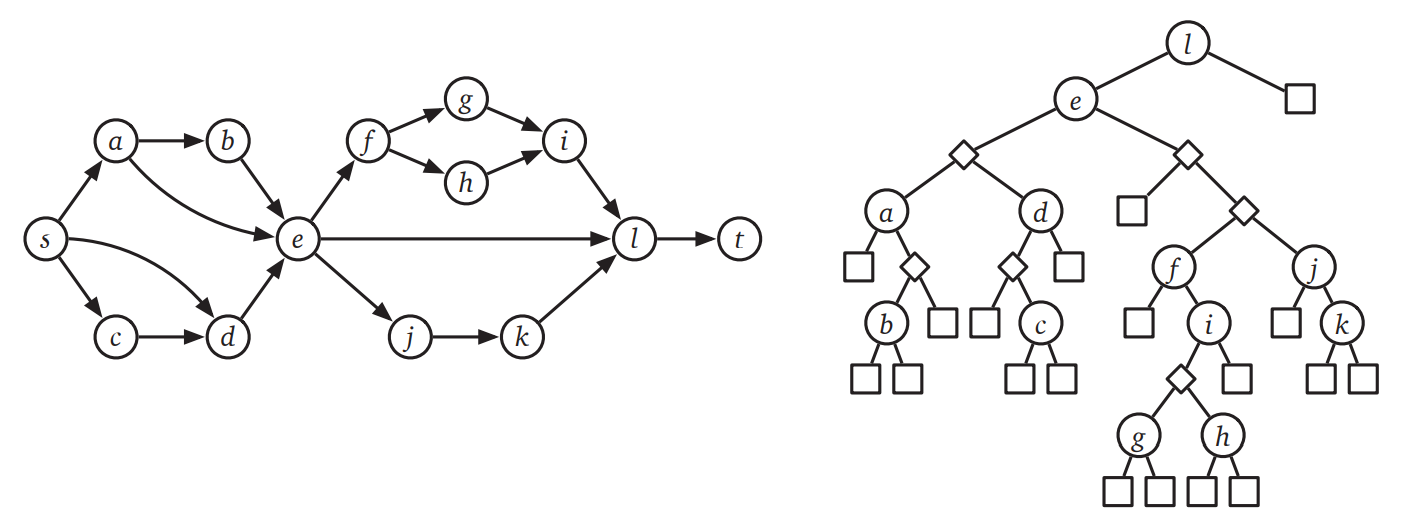 図 10.13直列-並列グラフと対応する分解木 (分解木において四角の頂点が葉を、ダイアモンドが並列頂点を表す)
図 10.13直列-並列グラフと対応する分解木 (分解木において四角の頂点が葉を、ダイアモンドが並列頂点を表す)-
有向グラフ \(G\) と二つの頂点 \(s, t\) が与えられたとします。\(G\) が \((s,t)\)-直列-並列グラフなら \(G\) の分解木を構築し、そうでない場合には分解木を構築できないと正しく報告するアルゴリズムを説明、解析してください。 [ヒント: 木を下から順に作ってください。]
-
辺が任意の実数で重み付されたフローネットワークの \((s,t)\)-直列-並列グラフが与えられたときに、そのネットワークの最大 \((s,t)\)-フローを計算するアルゴリズムを説明、解析してください。 [ヒント: (a) を使えば分解木が与えられたと考えることができます。まず最大フローの値を計算してから実際の最大フローを計算します。]
-
-
ネットワークの容量が小さな整数だけからなる場合には、増加路についての条件を緩和することで Edmonds-Karp の "最幅路" ヒューリスティックを高速化できます。つまりボトルネックの容量が最大の増加路を選ぶのではなく、次に示す容量縮小 (capacity scaling) アルゴリズムを使ってボトルネックの容量が最大値の半分以上の増加路を選ぶようにします (このアルゴリズムは Edmonds と Karp によって提案されました)。
辺容量が全て正の整数で、\(U = 2^{k}\) 以下であると仮定します (\(k\) はある整数)。このアルゴリズムはボトルネックの閾値 \(\Delta\) を管理します。最初 \(\Delta \leftarrow U\) とし、アルゴリズムは各フェーズにおいて残余グラフに含まれる有向路で最小容量が \(\Delta\) 以上であるものを探し、そのような有向路が無ければ \(\Delta \leftarrow \lfloor \Delta / 2 \rfloor\) として新しいフェーズを始めます。\(\Delta = 0\) となったらアルゴリズムは停止します。
-
辺の重みが整数の場合、最悪ケースにおいてアルゴリズムが実行するフェーズ数はいくつですか?
-
\(\Delta = \Delta\) であるフェーズが終わったときのフローが \(f\) だとします。残余グラフ \(G_{f}\) における最小カットの容量が最大でも \(E \cdot \Delta\) であることを示してください。
-
容量縮小の各フェーズにおける増加路は最大でも \(2E\) 個しかないことを示してください。
-
このアルゴリズム全体の実行時間はいくつですか?
-
-
私はこの話を Alexander Schrijver (アレキサンダー・シュライバー) による素晴らしいサーベイ "On the history of combinatorial optimization (till 1960)" で知りました。Harris-Ross レポートの機密指定は Schrijver による請求があって初めて解かれました。これからすぐに言及することになる Ford と Fulkerson は最大フロー最小カット問題を定式化した人物として Harris をあげていますが、本当に正確な歴史はよく分からない部分があります。というのも、Harris と Ross は "問題の定式化において助力を受けた" として George Danzig をあげているのです。[return]
-
T[homas] E. Harris and F[rank] S. Ross. Fundamentals of a method for evaluating rail net capacities. The RAND Corporation, Research Memorandum RM-1517, October 24, 1955. 米政府の著作によりパブリックドメイン (http://www.dtic.mil/dtic/tr/fulltext/u2/093458.pdf)[return]
-
Ford と Fulkerson も 1962 年に同じ悪い振る舞いをするネットワークを示しています。彼らのネットワークは 10 個の頂点と 48 個の辺からなります。[return]
-
Dinitz が発見した最大フローアルゴリズムはこれよりももっと複雑です。当時彼は Georgy Adelson-Velsky (ゲオルギー・アデルソン・ヴェルスキー、AVL 木の"AV") が担当するアルゴリズムの講義を受ける学生であり、Dinitz はそのアルゴリズムを練習問題の答として考案しました。このアルゴリズムも最短路に沿ってフローを追加していきますが、 追加の情報を保持することで実行時間を \(O(VE^{2})\) から \(O(V^{2}E)\) に落としています。[return]
-
表を小さくまとめるために、実行時間が辺の容量や最大フローの値に依存しているアルゴリズムは意図的に除外しました。この制限を考えたとしても、この表は全く不完全です![return]
-
もし just (...だけ) という副詞を使ったなら、あなたは無意識のうちに「私が詳細を詰める気にならないのでこれはまず間違いなく間違っているのだが、まぁとにかく私を信じてくれ」という言葉、あるいは「これはたぶん間違っている」という言葉を省略したと思うべきです。次の言葉にも注意: merely (ただ...)、simply (単純に...)、clearly (明らかに...)、obviously (自明に...)[return]