練習問題

  1. 有向グラフ \(G = (V, E)\) と二つの頂点 \(s, t\) と容量関数 \(c: E \rightarrow \mathbb{R}^{+}\) と \(f: E \rightarrow \mathbb{R}\) が与えられたとします。\(f\) が \(G\) の最大 \((s,t)\)-フローであるかを判定するアルゴリズムを説明してください。

  2. フローネットワーク \(G\) の実現可能な \((s,t)\)-フローを二つ取って \(f, f^{\prime}\) \((|f^{\prime}| > |f|)\) とします。残余グラフ \(G_{f}\) に実現可能な \((s,t)\)-フローであって値が \(|f^{\prime}| - |f|\) であるものが存在することを示してください。

  3. \(G\) を適当なフローネットワーク、\(u \rightarrow v\) を \(G\) の適当な辺とします。最小 \((s,t)\)-カット \((S, T)\) であって \(u \in S\) かつ \(v \in T\) となるものが存在するならば、最小カット \((S^{\prime}, T^{\prime})\) であって \(u \in T^{\prime}\) かつ \(v \in S^{\prime}\) となるものは存在しないことを証明してください。

  4. \((S, T)\) と \((S^{\prime}, T^{\prime})\) が適当なフローネットワーク \(G\) の最小 \((s,t)\)-カットであるとき、\((S \cap S^{\prime}, T \cup T^{\prime})\) と \((S \cup S^{\prime}, T \cap T^{\prime})\) も \(G\) の最小 \((s,t)\)-カットであることを証明してください。

  5. フローネットワーク \(G\) に逆向きの辺の組 \(u \rightarrow v\) と \(v \rightarrow u\) が両方含まれ、どちらも正の容量を持つとします。この二つの辺の容量を \(\min \lbrace c(u \rightarrow v), c(v \rightarrow u) \rbrace\) だけ減少させたフローネットワークを \(G^{\prime}\) とします。つまり \(G\) に対して次の操作を行って得られるグラフが \(G^{\prime}\) です:

    • \(c(u \rightarrow v) > c (v \rightarrow u)\) ならば、 \(u \rightarrow v\) の容量を \(c(u \rightarrow v) - c(v \rightarrow u)\) として \(v \rightarrow u\) を削除する。

    • \(c(u \rightarrow v) < c (v \rightarrow u)\) ならば、 \(v \rightarrow u\) の容量を \(c(v \rightarrow u) - c(u \rightarrow v)\) として \(u \rightarrow v\) を削除する。

    • \(c(u \rightarrow v) = c(v \rightarrow u)\) ならば、\(u \rightarrow v\) と \(v \rightarrow u\) の両方を削除する。

    1. \(G^{\prime}\) における最大 \((s,t)\)-フローは全て \(G\) における最大 \((s,t)\)-フローでもあることを証明してください (このことから、\(G\) に含まれる逆向きの辺の組を全て削除して得られるフローネットワークが、\(G\) と同じ最大フローを持つ逆向きの辺の組を持たないグラフであることが言えます)。

      辺が一方向にしかないという仮定を強制する
      図 10.11
      辺が一方向にしかないという仮定を強制する

    2. \(G^{\prime}\) における最小 \((s,t)\)-カットは全て \(G\) における最小 \((s,t)\)-カットでもあること、およびその逆を証明してください。

    3. \(G\) における最大 \((s,t)\)-フローであって \(G^{\prime}\) における最大 \((s,t)\)-フローでないものが少なくとも一つ存在することを示してください。

    1. 与えられたフローネットワークが唯一の最大 \((s,t)\)-フローを持つかどうかを判定する効率の良いアルゴリズムを説明してください。

    2. 与えられたフローネットワークが唯一の最小 \((s,t)\)-カットを持つかどうかを判定する効率の良いアルゴリズムを説明してください。

    3. 唯一の最大 \((s,t)\)-フローと複数の最小 \((s,t)\)-カットを持つフローネットワークを示してください。

    4. 複数の最大 \((s,t)\)-フローと唯一の最小 \((s,t)\)-カットを持つフローネットワークを示してください。

  7. ネットワーク \(G\) の \((s,t)\)-フローが非巡回 (acyclic) であるとは、正のフローを持つ辺からなる有向閉路が存在しないことを言います。つまり、正のフローを持つ辺からなる部分グラフが DAG ならばそのフローは非巡回です。

    1. 非巡回最大 \((s,t)\)-フローを計算するアルゴリズムを説明、解析してください。アルゴリズムの実行時間は漸近的に Ford-Fulkerson のアルゴリズムと同じであるべきです。

    2. 全ての \((s,t)\)-フローが非巡回であるかどうかを判定するアルゴリズムを説明、解析してください。

  8. \(G=(V,E)\) を辺の容量が全て \(1\) であるフローネットワークとし、\(s\) から \(t\) への最短路の長さが \(d\) 以下とします。

    1. 最大 \((s,t)\)-フローの値が \(E/d\) 以下であることを示してください。

    2. \(G\) が単純である、つまり任意の頂点 \(u\) と \(v\) の間には最大でも一つの辺しかないと仮定します (定義上はフローネットワークに平行辺が含まれていても構わないことに注意してください)。最大 \((s, t)\) -フローの値が \(O(V^{2}/d^{2})\) 以下であることを示してください。 [ヒント: 根が \(s\) である BFS 木において、平均の高さにある頂点はいくつですか？]

  9. 辺の容量が全て \(1\) であるフローネットワーク \(G=(V,E)\) と整数 \(k\) が与えられたとします。\(G\) から \(k\) 本の辺を削除してグラフに含まれる最大 \((s,t)\)-フローの値を最小にしたいときに、削除すべき \(k\) 本の辺を特定するアルゴリズムを説明、解析してください。

  10. フロー分解定理 の証明で行った解析はもっと厳密に行うことができます。 \(G = (V, E)\) を任意のフローネットワーク、\(f\) を \(G\) に含まれる任意の \((s,t)\)-フローとします。

    1. \(|f| = 0\) ならば \(f\) は最大でも \(E - V + 1\) 個の有向閉路の重み付き和であることを示してください。ただし和に現れる有向閉路に含まれる全ての辺 \(e\) は \(f(e) > 0\) を満たすとします。

    2. \(|f| > 0\) ならば \(f\) は最大でも \(E - V + 2\) 個の有向路または有向閉路の重み付き和であることを示してください。ただし和に現れる路と有向閉路に含まれる全ての辺 \(e\) は \(f(e) > 0\) を満たすとします。

    3. 前問の上界が厳密であることを示してください。つまり \(E-V+1\) 個より少ない有向閉路で分解できない循環と \(E - V + 2\) 個より少ない有向路と有向閉路で分解できないフローを示してください。 [ヒント: この問題は簡単です。]

  11. ♣ 任意の \((s,t)\)-フローの線形結合もまた \((s,t)\)-フローであるという観察から、任意のグラフにおける (実現可能でないものを含む) 全ての \((s,t)\)-フローは実線形空間をなすことが分かります。この線形空間のことをグラフのフロー空間 (flow space) と言います。

    1. 任意の連結グラフ \(G=(V, E)\) のフロー空間の次元は \(E - V + 2\) であることを示してください。

    2. \(T\) を \(G\) の任意の全域木とします。次の路と閉路の集合がフロー空間の基底となることを示してください。

      1. \(T\) における \(s\) から \(t\) への (唯一の) 路。

      2. 全ての \(e \notin T\) に対する、\(T \cup \lbrace e \rbrace\) に含まれる (唯一の) 閉路。

    3. \(T\) を \(G\) の任意の全域木、\(F\) を \(T\) の適当な辺を一つ削除して得られる森とします。次の路と閉路の集合がフロー空間の基底となることを示してください。

      1. \(F\) の二つの成分を繋いでいる全ての \(e \notin F\) に対する、\(F \cup \lbrace e \rbrace\) に含まれる (唯一の) \(s\) から \(t\) への路。

      2. \(F\) の同じ成分を繋いでいる全ての \(e \notin F\) に対する、\(F \cup \lbrace e \rbrace\) に含まれる (唯一の) 閉路。

    4. 次の主張を証明または反証してください: 「任意の連結フローネットワークには、\(s\) から \(t\) への単純路だけからなるフロー空間の基底が存在する」

  12. カットが頂点の分割ではなくてグラフの辺の部分集合として定義されることもあります。この問題ではこの二つの定義がほぼ同値であることを示します。

    有向辺の集合 \(X\) が \(s\) と \(t\) を分離するとは、\(s\) から \(t\) への任意の有向路が少なくとも一つの \(X\) の要素を含むことを言います。また任意の頂点集合 \(S\) について、\(S\) から出る辺の集合を \(\pmb{\delta S}\) で表すことにします。つまり \(\delta S :=\) \(\lbrace u \rightarrow v\ |\ u \in S, v \notin S \rbrace\) です。

    1. \((S, T)\) が \((s,t)\)-カットならば \(\delta S\) が \(s\) と \(t\) を分離することを示してください。

    2. \(s\) と \(t\) を分離する任意の辺集合を \(X\) とします。\((s,t)\)-カット \((S, T)\) であって \(\delta S \subseteq X\) を満たすものが存在することを示してください。

    3. \(s\) と \(t\) を分離する最小の辺集合を \(X\) とします (このような辺集合を帯 (bond) と呼ぶこともあります)。\((s,t)\)-カット \((S, T)\) であって \(\delta S = X\) を満たすものが存在することを示してください。

  13. ネットワークの各辺 \(u \rightarrow v\) に付いているのが容量ではなくて非負の需要 (demand) であるとします。このとき \((s,t)\)-フロー \(f\) が実現可能とは、任意の辺 \(u \rightarrow v\) に対して \(f(u \rightarrow v) \geq d(u \rightarrow v)\) であることを言います。この設定における問題として自然なのは、実現可能な \((s,t)\)-フローであって値が最小のものを考える問題です。

    1. グラフと需要関数と \(s,t\) が与えられたときに、実現可能な最小 \((s,t)\)-フローを計算する効率の良いアルゴリズムを説明してください。 [ヒント: 全ての辺においてゼロでないフローを見つけ、実現可能になるまで大きくする。]

    2. 辺に容量の付いたグラフの最大フローを計算するサブルーチン \(\textsc{MaxFlow}\) を使えると仮定したときに、与えられたグラフと辺の需要に対する最小フローを計算する効率の良いアルゴリズムを説明してください。アルゴリズムが \(\textsc{MaxFlow}\) を使うのは一度だけとしてください。

    3. 需要という言葉を使って最大フロー最小カット定理に似たものを述べ、それを証明してください。(最小フローが最大カットと対応しますか？)

  14. 任意のフローネットワーク \(G\) と頂点 \(u, v\) について、\(u\) から \(v\) への任意の路に含まれる辺の最小容量の最大値を \(\mathit{bottleneck}_{G}(u, v)\) とします。

    1. \(\mathit{bottleneck}_{G}(s, t)\) の値を \(O(E \log V)\) 時間で求めるアルゴリズムを説明、解析してください。この値は Edmonds-Karp の "最幅増加路" アルゴリズム の最初の反復において追加されるフローの値です。

    2. \(G\) が無向である、あるいは全ての辺に対して \(c(u \rightarrow v) = c(v \rightarrow u)\) であるとします。\(\mathit{bottleneck}_{G}(u, v)\) を \(O(V + E)\) 時間で計算するアルゴリズムを説明、解析してください。有向グラフに対してこのアルゴリズムを適用できないのはどうしてですか？ [ヒント: 辺容量の中央値を見つける。]

    3. ❤ フローネットワーク \(G\) が無向であると仮定します。\(G\) の全域木 \(T\) であって任意の頂点 \(u, v\) について \(\mathit{bottleneck}_{T} (u, v) = \mathit{bottleneck}_{G} (u,v)\) であるものを構築するアルゴリズムを説明、解析してください (\(T\) の辺の容量は \(G\) と同じです)。満点のためには、アルゴリズムの実行時間が \(O(E)\) 時間であることが求められます。

  15. 辺に整数の重みのついたフローネットワークを \(G\) とし、\(G\) の整数最大フローを \(f^{\ast}\) とします。次の操作に対するアルゴリズムを説明してください:

    1. \(\textsc{Increment}(e)\): 辺 \(e\) の容量を \(1\) 増やし、最大フローを更新する。
    2. \(\textsc{Decrement}(e)\): 辺 \(e\) の容量を \(1\) 減らし、最大フローを更新する。

    二つのアルゴリズムは \(f^{\ast}\) を使って最大フロー(再)計算し、実行時間は最大フローを最初から計算するよりも短くあるべきです。

  16. 辺に整数の容量がついたネットワークを \(G\) とします。\(G\) の辺が upper-binding であるとは、その辺の容量を \(1\) 増やすと \(G\) の最大フローの値が増加することを言います。同様に \(G\) の辺が lower-binding であるとは、その辺の容量を減らすと \(G\) の最大フローの値が減少することを言います。

    1. どんなネットワーク \(G\) にも upper-binding な辺が含まれますか？ 答えが正しいことを証明してください。

    2. どんなネットワーク \(G\) にも lower-binding な辺が含まれますか？ 答えが正しいことを証明してください。

    3. \(G\) に含まれる upper-binding な辺を全て見つけるアルゴリズムを説明してください。入力は \(G\) と \(G\) の最大フローで、実行時間は \(O(E)\) としてください。

    4. \(G\) に含まれる lower-binding な辺を全て見つけるアルゴリズムを説明してください。入力は \(G\) と \(G\) の最大フローで、実行時間は \(O(EV)\) としてください。

  17. 与えられたフローネットワーク \(G\) が複数の最小 \((s,t)\)-カットを持つとします。最良の最小 \((s,t)\)-カット \((S, T)\) を、最小 \((s,t)\)-カットの中で \(S\) から \(T\) に向かう辺の数が最小なものとして定義します。

    1. 辺の容量が整数のときに、最良の最小 \((s,t)\)-カットを見つける効率の良いアルゴリズムを説明してください。

    2. 辺の容量が任意の実数のときに、最良の最小 \((s,t)\)-カットを見つける効率の良いアルゴリズムを説明してください。

    3. 与えられたネットワークの最良の最小 \((s,t)\)-カットが唯一であるかどうかを判定する効率の良いアルゴリズムを説明してください。

  18. 最大フローを初めて教えることになった新米の助教授は、Ford-Fulkerson の一般的な増加路アルゴリズムを "貪欲に" した次のアルゴリズムを生徒に示しました。このアルゴリズムを使えば残余グラフを作る代わりに増加路に沿って辺の容量を減らすだけ1で済みます！ 辺を飽和させるときにはただグラフから取り除けばいいのです。残余グラフとかいう、わけの分からないものなんて考えなくていいでしょう？

    procedure \(\texttt{GreedyFlow}\)(\(G,c,s,t\))

    for \(G\) の辺 \(e\) do

    \(f(e) \leftarrow 0\)

    while \(G\) に \(s\) から \(t\) への路がある do

    \(\pi \leftarrow s\) から \(t\) への適当な路

    \(F \leftarrow \pi\) に含まれる容量が最小の辺

    for \(e \in \pi\) do

    \(f(e) \leftarrow f(e) + F\)

    if \(c(e) = F\) then

    \(e\) を \(G\) から削除する

    else

    \(c(e) \leftarrow c(e) - F\)

    1. \(\textsc{GreedyFlow}\) が常に最大フローを計算するわけではないことを示してください。

    2. \(\textsc{GreedyFlow}\) が最大フローの良い近似を計算することさえ保証されていないことを示してください。つまり、任意の \(\alpha > 1\) についてあるフローネットワーク \(G\) が存在して、\(G\) の最大フローの値が \(\textsc{GreedyFlow}\) の計算するフローの値の \(\alpha\) 倍よりも大きくなることを示してください。 [ヒント: \(\textsc{GreedyFlow}\) の各反復において最悪の路 \(\pi\) が選ばれると仮定してください。]

  19. Maurice Queyranne (モーリス・クイラン) は 1980 年、Edmonds と Karp の"最幅路" ヒューリスティックが停止しないようなネットワークの例を発表しました。オリジナルの Ford-Fulkerson のアルゴリズムに対する Zwick の例 と同じように、この例でも \(\phi = (\sqrt{5} - 1) / 2\) が使われます。下図における三つの垂直な辺が Zwick の例における三つの水平な線と本質的に同じ役目を果たします。

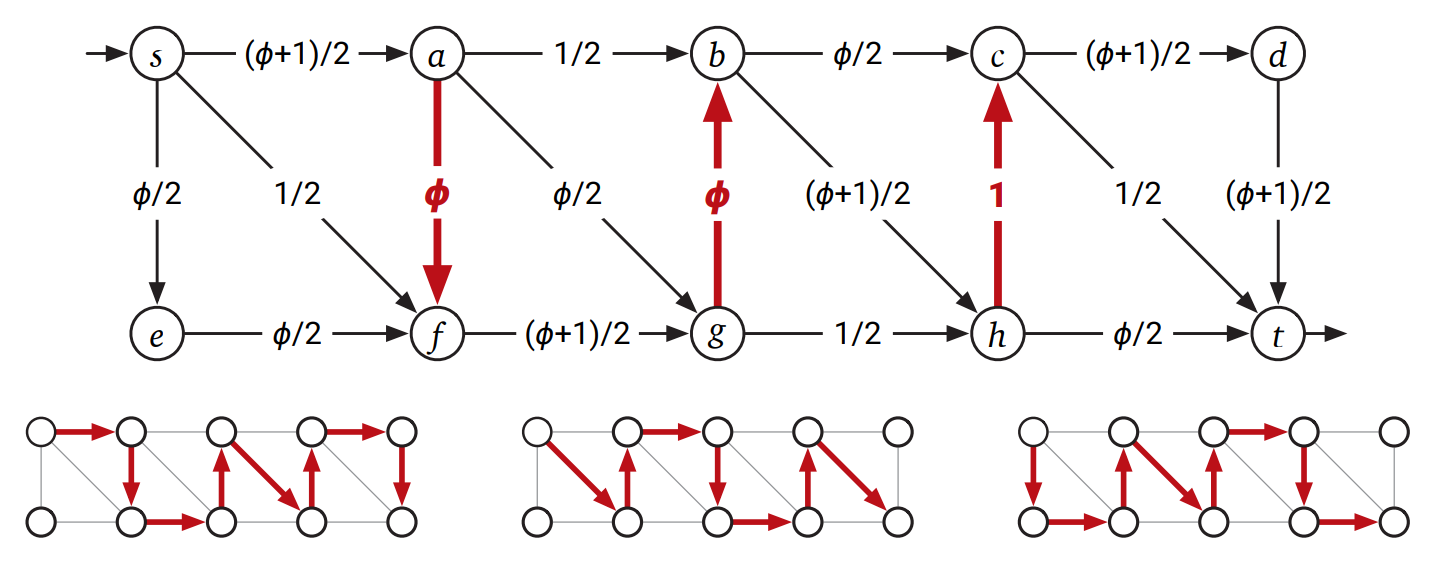    Queyranne のネットワークとその「最幅」増加路
    図 10.12
    Queyranne のネットワークとその「最幅」増加路

    1. 次の操作の無限列が Edmonds-Karp の "最幅路" アルゴリズムの実行したときの操作列として正しいことを示してください (図の下部も参照)。

      procedure \(\texttt{QueyranneFatPaths}\)()

      for \(i \leftarrow 1\) to \(\infty\) do

      \(\phi^{3i-2}\) のフローを \(s \rightarrow a \rightarrow f \rightarrow g \rightarrow b \rightarrow h \rightarrow c \rightarrow d \rightarrow t\) に流す

      \(\phi^{3i-1}\) のフローを \(s \rightarrow f \rightarrow a \rightarrow b \rightarrow g \rightarrow h \rightarrow c \rightarrow t\) に流す

      \(\phi^{3i}\) のフローを \(s \rightarrow e \rightarrow f \rightarrow a \rightarrow g \rightarrow b \rightarrow c \rightarrow h \rightarrow t\) に流す

    2. Queyranne のネットワークにおいて最大フローを出力する \(O(1)\) 個の増加路の列を示してください。

  20. ❤ \(\pmb{(s, t)}\)-直列-並列グラフ とは、特別な二つの頂点 \(s,t\) を持つ有向非巡回グラフであって次の条件のうちどれかを満たすものを言います:

    • ベースケース: \(s\) から \(t\) への有向辺だけからなるグラフ。

    • 直列: \((s,u)\)-直列-並列グラフと \((u,t)\)-直列-並列グラフの和集合。ただし二つのグラフに共通する頂点は \(u\) だけ。

    • 並列: 二つの \((s,t)\)-直列-並列グラフの和集合。ただし二つのグラフに共通する頂点は \(s\) と \(t\) だけ。

    任意の \((s,t)\)-直列-並列グラフ \(G\) は分解木 (decomposition tree) を使って表すことができます。分解木の頂点には三つの種類があり、それぞれ (\(G\) の辺を表す) 葉と (\(s\) と \(t\) 以外の頂点を表す) 直列頂点および並列頂点です。一つの直列-並列グラフに複数の分解木が存在することがあり得ます。

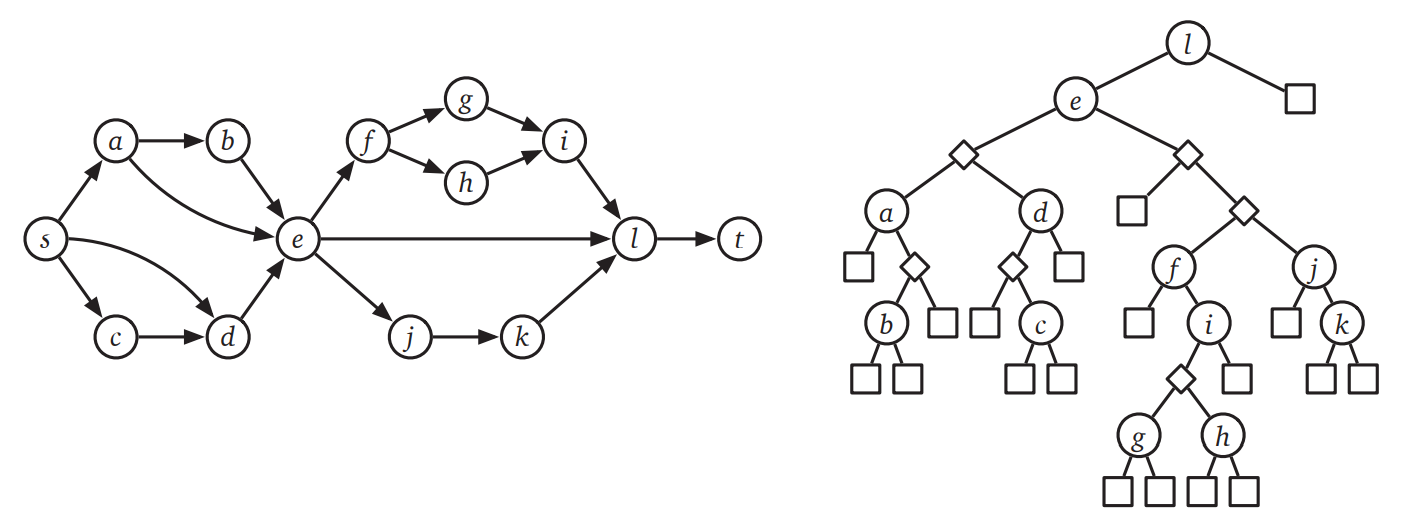    直列-並列グラフと対応する分解木 (分解木において四角の頂点が葉を、ダイアモンドが並列頂点を表す)
    図 10.13
    直列-並列グラフと対応する分解木 (分解木において四角の頂点が葉を、ダイアモンドが並列頂点を表す)

    1. 有向グラフ \(G\) と二つの頂点 \(s, t\) が与えられたとします。\(G\) が \((s,t)\)-直列-並列グラフなら \(G\) の分解木を構築し、そうでない場合には分解木を構築できないと正しく報告するアルゴリズムを説明、解析してください。 [ヒント: 木を下から順に作ってください。]

    2. 辺が任意の実数で重み付されたフローネットワークの \((s,t)\)-直列-並列グラフが与えられたときに、そのネットワークの最大 \((s,t)\)-フローを計算するアルゴリズムを説明、解析してください。 [ヒント: (a) を使えば分解木が与えられたと考えることができます。まず最大フローの値を計算してから実際の最大フローを計算します。]

  21. ネットワークの容量が小さな整数だけからなる場合には、増加路についての条件を緩和することで Edmonds-Karp の "最幅路" ヒューリスティックを高速化できます。つまりボトルネックの容量が最大の増加路を選ぶのではなく、次に示す容量縮小 (capacity scaling) アルゴリズムを使ってボトルネックの容量が最大値の半分以上の増加路を選ぶようにします (このアルゴリズムは Edmonds と Karp によって提案されました)。

    辺容量が全て正の整数で、\(U = 2^{k}\) 以下であると仮定します (\(k\) はある整数)。このアルゴリズムはボトルネックの閾値 \(\Delta\) を管理します。最初 \(\Delta \leftarrow U\) とし、アルゴリズムは各フェーズにおいて残余グラフに含まれる有向路で最小容量が \(\Delta\) 以上であるものを探し、そのような有向路が無ければ \(\Delta \leftarrow \lfloor \Delta / 2 \rfloor\) として新しいフェーズを始めます。\(\Delta = 0\) となったらアルゴリズムは停止します。

    1. 辺の重みが整数の場合、最悪ケースにおいてアルゴリズムが実行するフェーズ数はいくつですか？

    2. \(\Delta = \Delta\) であるフェーズが終わったときのフローが \(f\) だとします。残余グラフ \(G_{f}\) における最小カットの容量が最大でも \(E \cdot \Delta\) であることを示してください。

    3. 容量縮小の各フェーズにおける増加路は最大でも \(2E\) 個しかないことを示してください。

    4. このアルゴリズム全体の実行時間はいくつですか？

  1. もし just (...だけ) という副詞を使ったなら、あなたは無意識のうちに「私が詳細を詰める気にならないのでこれはまず間違いなく間違っているのだが、まぁとにかく私を信じてくれ」という言葉、あるいは「これはたぶん間違っている」という言葉を省略したと思うべきです。次の言葉にも注意: merely (ただ...)、simply (単純に...)、clearly (明らかに...)、obviously (自明に...)[return]

広告
このページの文章はテキストゆれないくんを使って校正されました。