フロー

\(\pmb{(s, t)}\)-フロー (ソースとシンクが明らかな場合には単にフロー) とは、関数 \(f:E \rightarrow \mathbb{R}\) であって \(s,t\) 以外の全ての頂点 \(v\) において次の保存条件 (conservation constraint) が満たされるものを言います: \[ \sum_{u} f(u \rightarrow v) = \sum_{w} f(v \rightarrow w) \]

保存条件を言葉を使って言い換えれば、全ての頂点 \(v\) に対して \(v\) に入るフローと \(v\) から出るフローが等しいということです。記法を単純にするために、辺 \(u \rightarrow v\) が存在しない場合には \(f(u \rightarrow v) = 0\) と定義します。フロー \(f\) の値 (value) \(|f|\) とはソース頂点 \(s\) から出るフローの和です: \[ |f| := \sum_{w} f(s \rightarrow w) - \sum_{u} f(u \rightarrow s) \]

\(|f|\) がシンク頂点 \(t\) へ向かうフローの和とも等しいことを示すのは難しくありません。記法を単純にするために、\(\pmb{\partial f(v)}\) で頂点 \(v\) から出るフローを表すことにします: \[ \partial f (v) := \sum_{w} f(v \rightarrow w) - \sum_{u} f(u \rightarrow v) \] 保存条件から \(s, t\) 以外の頂点 \(v\) について \(\partial f(v) = 0\) であり、したがって \[ \sum_{v} \partial f(v) = \partial f(s) + \partial f(t) \] です。一方で全てのフローはある頂点から出て他の頂点に入るので \(\sum_{v} \partial f (v) = 0\) であり、したがって \(|f| = \partial f(s) = - \partial f(t)\) が成り立ちます。

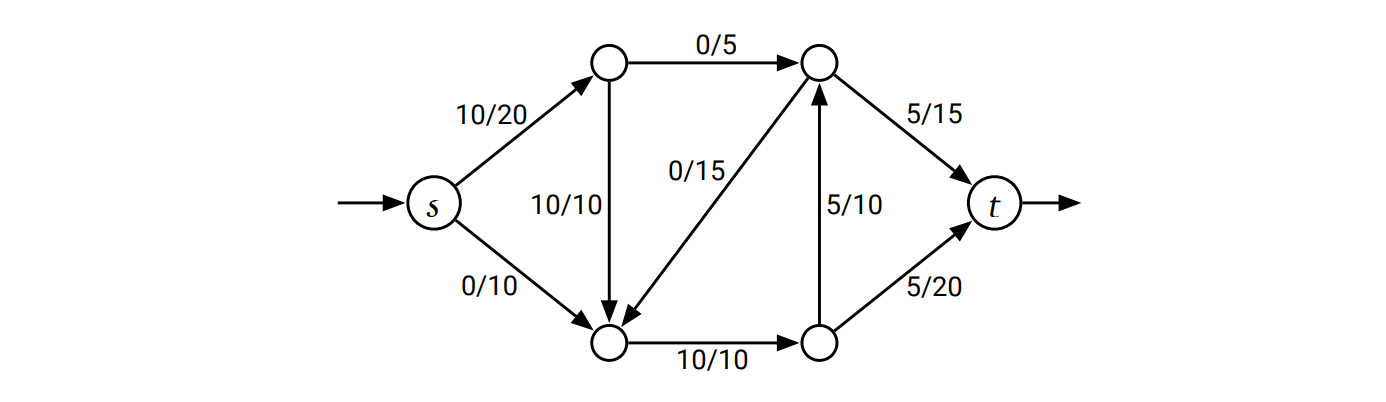
ここでグラフの辺に非負の容量 (capacity) を割り当てるもう一つの関数 \(c: E \rightarrow \mathbb{R}_{\geq 0}\) が追加で与えられたとします。フロー \(f\) が容量 \(c\) に対して実現可能 (feasible) であるとは、全ての辺 \(e\) に対して \(0 \leq f(e) \leq c(e)\) が成り立つことを言います。フローを考えると言った場合に通常考えるのは、何らかの固定された容量関数 \(c\) に対する実現可能なフローです。またフロー \(f\) と容量関数 \(c\) について、辺 \(e\) で \(f(e) = c(e)\) が成り立つならば \(f\) は \(e\) を 飽和 (saturate) させると言い、\(f(e) = 0\) ならば \(f\) は \(e\) を避ける (avoid) と言います。

最大フロー問題 (maximum flow problem) とは、与えられた有向グラフと容量関数に対する実現可能な \((s,t)\)-フローであって値が最大のものを計算する問題です。