Ford と Fulkerson の増加路アルゴリズム

Ford と Fulkerson が示した最大フロー最小カット定理の証明から、最大フローを計算するアルゴリズムが直ちに手に入ります: 空のフローから始め、残余グラフにおける \(s\) から \(t\) への任意の増加路を使ってフローを増加させる処理を増加路が無くなるまで繰り返すというものです。

このアルゴリズムについての次の系は簡単に示せますが、重要です:

実際の最大フローを \(f^{\ast}\) とすると、辺の容量が整数のネットワークに対する Ford-Fulkerson のアルゴリズムは大きく見積もっても最大 \(|f^{\ast}|\) 回の反復の後に停止します。各反復においてこのアルゴリズムは増加路を見つけるための何か優先探索と残余グラフ \(G_{f}\) の構築を \(O(E)\) 時間で行うので、この設定における最悪実行時間は \(\pmb{O(E|f^{\ast}|)}\) です。

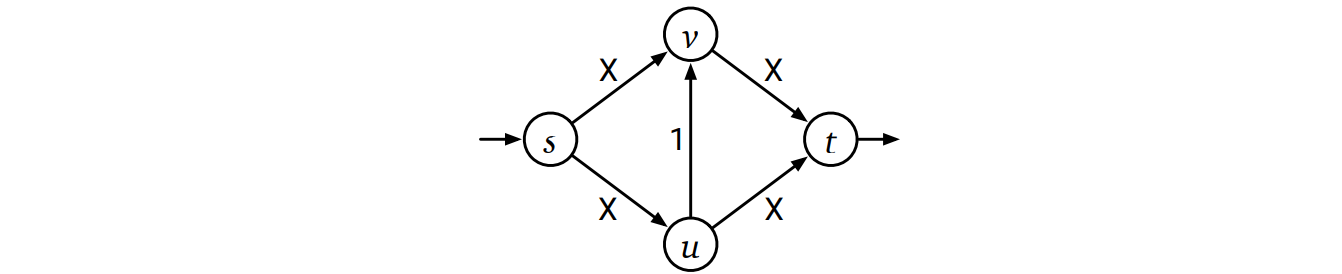
Jack Edmonds と Richard Karp はこの実行時間解析が本質的に厳密であることを証明しました。次の図にある四つの頂点を持つネットワークを考えます。ここで \(X\) はとても大きい整数を表します。このネットワークにおける最大フローの値は明らかに \(2X\) です。しかし Ford-Fulkerson のアルゴリズムは増加路 \(s \rightarrow u \rightarrow v \rightarrow t\) を使って \(1\) だけフローを増加させ、その後増加路 \(s \rightarrow v \rightarrow u \rightarrow t\) を使って \(1\) だけフローを増加させるという処理を繰り返すかもしれません。この場合実行時間は \(\Theta(X) = \Omega(|f^{\ast}|)\) となります。

現実のデータから作られるグラフの多く、あるいは \(|f^{\ast}|\) が小さいという条件においては、Ford-Fulkerson のアルゴリズムはとても高速に動作します。しかし増加路に制限を設けなければ、最悪計算時間が効率的だとは言えません。Edmonds と Karp が示した上記のネットワークは \(O(\log X)\) ビットで表現できるので、Ford-Fulkerson の実行時間は実は入力サイズに対して指数的だからです。

無理数の容量

では容量が整数でなかったら？ 容量に (正の) 定数をかければ最大フローは同じだけ大きくなるので、辺の重みが有理数の場合には Ford-Fulkerson のアルゴリズムを使って最大フローを求められます。ただしこの場合でも計算時間は (入力を表現するためのビット長に対して) 指数的です。

一方で無理数の容量がある場合、アルゴリズムがどんどん小さくなる増加路を選び続けて停止しないことがあります。さらに悪いことに、この増加していくフローの無限列が最大フローに収束しない、さらには最大フローからかけ離れた値に収束することがあります！ この悪い振る舞いをするネットワークの最小の例は 1993 年に Uri Zwick (ユリ・ツウィック) によって発見されました¹:

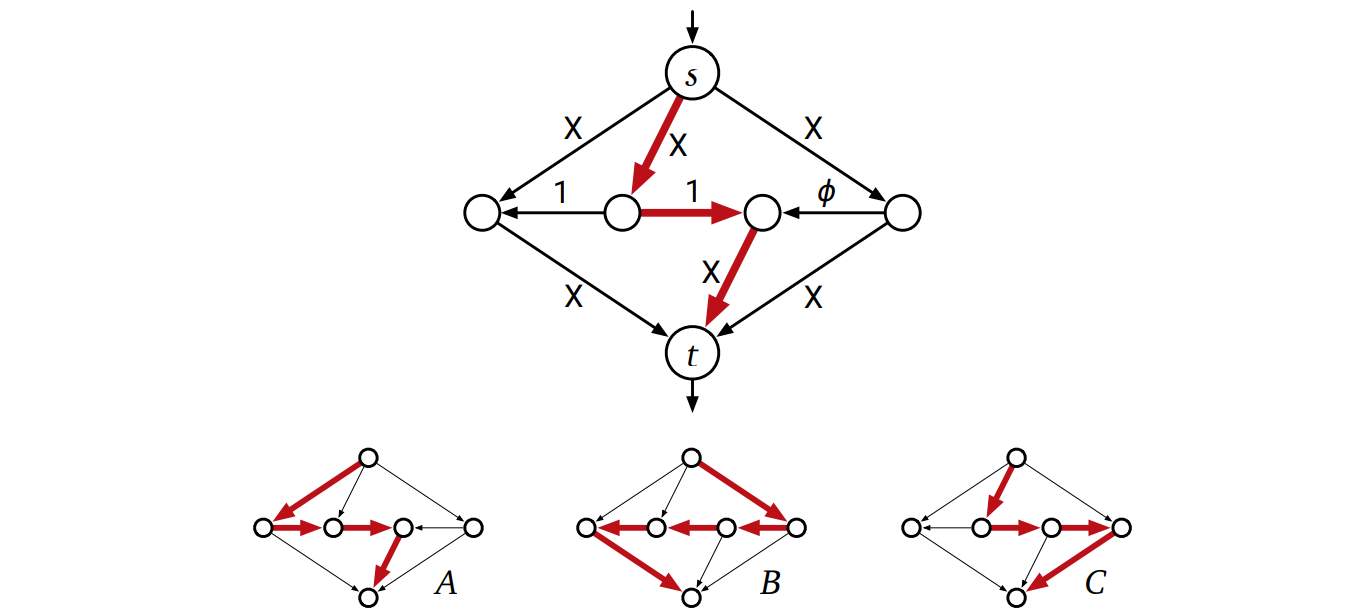
このネットワークに含まれる 9 個の辺のうち 6 個にはとても大きい整数の重み \(X\) が付いており、2 個には重み \(1\) が、1 個には重み \(\phi = (\sqrt{5} - 1) / 2 \approx 0.618034\) が付いています。\(\phi\) は \(1 - \phi = \phi^{2}\) を満たすように選ばれています。Ford-Fulkerson のアルゴリズムがスタックすることを示すために、アルゴリズムが進行するにつれて三つの水平な辺の残余容量がどのように変化するかに注目します (他の 6 つの辺の残余容量は常に \(X - 1\) 以上です)。

Ford-Fulkerson のアルゴリズムが最初に上図の上部にある増加路を選んだとします。このとき三つの水平な辺の残余容量は左から順に 1, 0, \(\phi\) となります。ある整数 \(k\) に対して三つの水平な辺の残余容量が \(\phi^{k-1}\), \(0\), \(\phi^{k}\) であると帰納的に仮定すると、このとき

1. 増加路 \(B\) に沿ってフローを \(\phi^{k}\) だけ増加させると、残余容量は \(\phi^{k+1}\), \(\phi^{k}\), \(0\) となる。

2. 続いて増加路 \(C\) に沿ってフローを \(\phi^{k}\) だけ増加させると、残余容量は \(\phi^{k+1}\), \(0\), \(\phi^{k}\) となる。

3. 続いて増加路 \(B\) に沿ってフローを \(\phi^{k+1}\) だけ増加させると、残余容量は \(0\), \(\phi^{k+1}\), \(\phi^{k+2}\) となる。

4. 続いて増加路 \(A\) に沿ってフローを \(\phi^{k+1}\) だけ増加させると、残余容量は \(\phi^{k+1}\), \(0\), \(\phi^{k+2}\) となる。

が成り立ちます。よって帰納法により、\(4n + 1\) 回の増加ステップの後には残余容量が \(\phi^{2n-2}\), \(0\), \(\phi^{2n-1}\) となることが分かります。増加の回数を無限大にすると、フローの値は \[ 1 + 2 \sum_{i=1}^{\infty} \phi^{i} = 1 + \frac{2}{1 - \phi} = 4 + \sqrt{5} < 7 \] に収束します。しかし最大フローの値は明らかに \(2X + 1 \gg 7\) です。

実際の実装を考える読者は、なぜそもそも無理数の容量なんてものを考えるのかと不思議に思うかもしれません。コンピューターが正確に表現できるのは (小さな) 整数と (小さい、二進の) 分数だけなのにどうして、と。いい質問です！ この質問に対する数学者の答えは「容量の整数への制限は文字通り人工的だから」です。容量が整数にしかならないというのはコンピューターのハードウェア (あるいはハードウェアに関連する物理法則) が作り出した人為的な制限であって、抽象的な計算問題が持つ本質的な特徴ではありません。より実際的な理由としては、無理数の入力に対するアルゴリズムの振る舞いを見ることで、浮動小数点数を含んだ入力に対する最悪ケースにおける振る舞いが分かるからというのがあります ――つまり、ひどいのです。常識的な容量を持つインスタンスであっても、よく考えずに Ford-Fulkerson のアルゴリズムを実装すると、浮動小数の切り捨て誤差だけが原因で無限ループに入ってしかも正しい答えに近づかないことがあります。

1. Ford と Fulkerson も 1962 年に同じ悪い振る舞いをするネットワークを示しています。彼らのネットワークは 10 個の頂点と 48 個の辺からなります。^[return]