最小全域木

みなさん、我々はみな団結しなければなりません。

さもなければ、我々は別々に吊るし首にされるでしょう。

――Benjamin Franklin, 独立宣言の壇上で (July 4, 1776)

その論文を投稿すべきかどうかについて誰かからのアドバイスを求めていた ――いったいそんなアドバイスをできる人がいたのでしょうか？―― ことを覚えています。その論文の議論はとても簡単でしたから...。彼が投稿するように言ってくれて良かったです。それから何年もたっていますが、このとても単純な論文と同じぐらい有名になった私の論文は他にありません。

――Joseph Kruskal, 自身の最小全域木アルゴリズムを説明して (1997)

スベテをカタヅケロ！

――Allie Brosh, "This is Why I'll Never be an Adult", Hyperbole and a Half, June 17, 2010

辺に重みの付いた連結無向グラフが与えられたとします。つまり、グラフ \(G=(V,E)\) と辺 \(e\) に実数の重み \(w(e)\) を割り当てる重み関数 \(w: E \to \mathbb{R}\) が与えられます (重みは正でもゼロでも負でもあり得ます)。この章で説明するのは、\(G\) の最小全域木 (minimum spanning tree, MST) を見つけるアルゴリズムです。最小全域木とは全域木 \(T\) であって次の関数を最小にするものです: \[ w(T) := \sum_{e \in T} w(e) \]

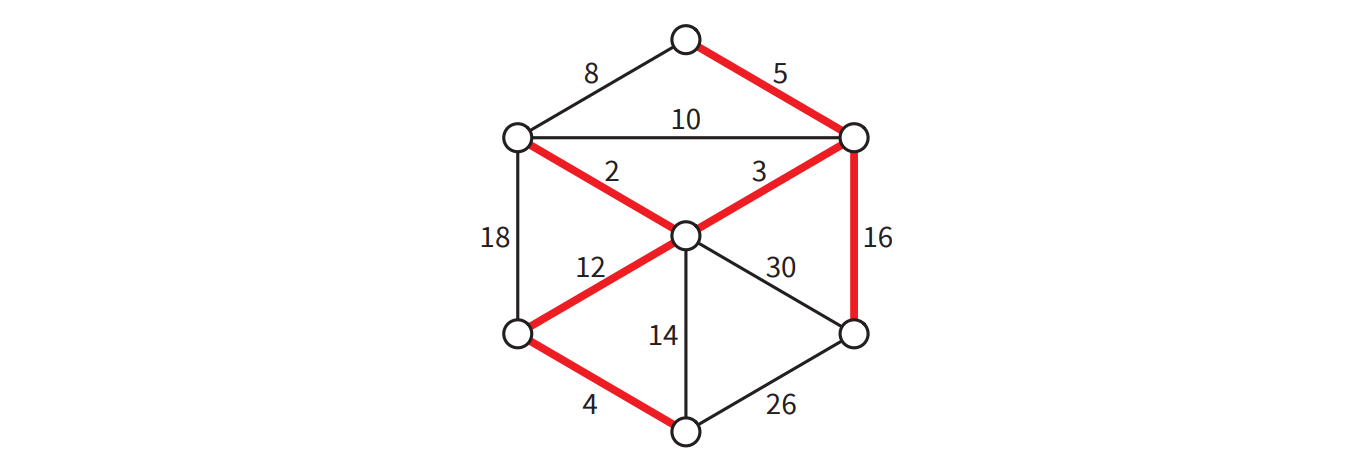
重み付きグラフとその最小全域木
図 7.1
重み付きグラフとその最小全域木

辺の重みが異なる場合

最小全域木問題が厄介なのは、グラフに重みが同じ最小全域木が複数存在することがあり得る点です。例えば \(G\) の全ての辺の重みが \(1\) の場合、\(G\) の全ての全域木が重み \(V-1\) の最小全域木です。最小全域木が複数あるとアルゴリズムの開発が複雑になるので、最小全域木が一つだけだと仮定できれば話が単純になります。

幸いにも、最小全域木が唯一であることを保証する簡単な条件があります。

命題 7.1 連結グラフ \(G\) の辺の重みが全て異なる場合、\(G\) は唯一の最小全域木を持つ1。

証明 適当なグラフ \(G\) が二つの最小全域木 \(T, T^{\prime}\) を持つとする。\(G\) に含まれる辺の組が同じ重みを持つことをこれから示す。この証明が本質的に使っているのは、貪欲アルゴリズムの正しさの証明に用いた交換の議論である。

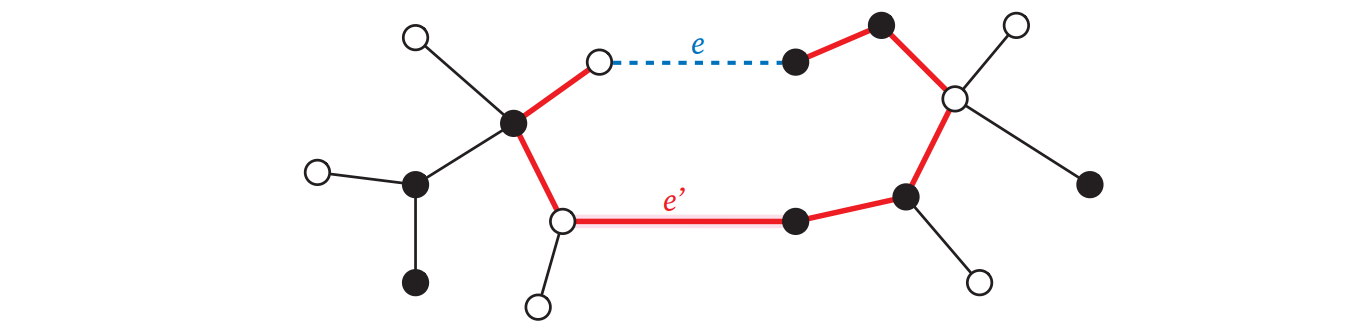
二つの全域木にはお互いに相手に存在しない辺が含まれる。\(e\) を \(T \backslash T^{\prime}\) に含まれる重みが最小の辺、\(e^{\prime}\) を \(T^{\prime} \backslash T\) に含まれる重みが最小の辺とする (重みが最小の辺が複数ある場合には適当に選ぶ)。一般性を失うことなく \(w(e) \leq w(e^{\prime})\) と仮定する。

部分グラフ \(T^{\prime} \cup \lbrace e \rbrace\) にはちょうど一つの閉路 \(C\) が含まれ、\(C\) は \(e\) を通る。\(e^{\prime\prime}\) を \(C\) に含まれて \(T\) に含まれない辺とする。\(T\) は木だから、そのような辺は必ず存在する (\(e^{\prime\prime} = e^{\prime}\) かもしれないし、そうでないかもしれない)。\(e \in T\) と \(e^{\prime\prime} \notin T\)より \(e^{\prime\prime} \neq e\) であり、よって \(e^{\prime\prime} \in T^{\prime} \backslash T\) である。したがって \(w(e^{\prime\prime}) \geq w(e^{\prime}) \geq w(e)\) が分かる。

全域木 \(T^{\prime\prime} = T^{\prime} + e - e^{\prime\prime}\) を考える (\(T^{\prime\prime}\) は \(T\) に等しいかもしれない)。このとき \(w(T^{\prime\prime}) = w(T^{\prime}) + w(e) - w(e^{\prime\prime}) \leq w(T^{\prime})\) となるが、\(T^{\prime}\) は最小全域木なので、\(w(T^{\prime\prime}) = w(T^{\prime})\) となる。つまり、\(T^{\prime\prime}\) もまた最小全域木である。したがって \(w(e) = w(e^{\prime\prime})\) であり、証明したい式が得られた。 \(\Box\)

procedure \(\texttt{ShorterEdge}\)(\(i,j,k,l\))

if \(w(i, j) < w(k, l)\) then

return \((i, j)\)

else if \(w(i, j) > w(k, l)\) then

return \((k, l)\)

else if \(\min(i, j) < \min(k, l)\) then

return \((i, j)\)

else if \(\min(i, j) > \min(k, l)\) then

return \((k. l)\)

else if \(\max(i, j) < \max(k, l)\) then

return \((i, j)\)

else

\(\color{maroon}{\langle \langle \max(i, j) > \max(k, l) \rangle \rangle}\)

return \((k. l)\)

同じ重みを持つ辺が複数ある場合の一貫した辺の選び方を決めておけば、辺の重みが異なるグラフに対するアルゴリズムを同じ重みを持つ辺のあるグラフに対するアルゴリズムに変形できます。上に示したのは一例です。\(\textsc{ShorterEdge}\) は四つの (異なるとは限らない) 頂点 \(i,j,k,l\) を受け取り、\((i, j)\) と \((k, l)\) のどちらが "短い" かを返します (入力は無向グラフであり、\((i, j)\) と \((j, i)\) が同じ辺を表すことに注意してください)。

命題 7.1 より、この選び方を使えば任意のグラフの最小木が唯一となります。よって、これからこの章では辺の重さが異なるグラフが常に与えられ、その最小全域木は常に一つだけであると仮定しても問題ありません。つまり「グラフの最小全域木を... (the minimum spanning tree ...)」と書いたとしても曖昧さは生じません。

唯一の全域最小木アルゴリズム

最小全域木を計算するアルゴリズムはたくさんありますが、そのほとんどはこれから説明する一般的な戦略のインスタンスと言うことができます。これはグラフ探索アルゴリズムにおいて、たくさんの異なるアルゴリズムが何か優先探索という一般的なアルゴリズムの変種だったことに似ています。

一般的な最小全域木アルゴリズムは入力グラフ \(G\) の非巡回部分グラフ \(F\) を管理します。\(F\) は中間全域森 (intermediate spanning forest) と呼ばれ、アルゴリズムの各時点において次の不変条件を満たします:

\(F\) は \(G\) の最小全域木の部分グラフである。

一般的な最小全域木アルゴリズムは \(G\) の頂点一つずつからなる森を \(F\) とした状態から始まり、各反復で頂点の間に辺を加えて木をつなげていきます。アルゴリズムが停止したとき \(F\) は一つの全域木となり、不変条件からそれが \(G\) の最小全域木となるという寸法です。もちろん最小全域木に含まれない辺も存在するので、森に加える辺は慎重に選ばなければなりません。

森に辺を加えるとき、グラフの辺は中間全域森 \(F\) によって三つに分類されます:

全ての最小全域木アルゴリズムは二つの単純な観察に基づいています。一つ目の観察は Robert Prim (ロバート・プリム) によって 1957 年に証明されたもので (ただしそれよりも前のアルゴリズムにも暗黙の内に含まれていましたが)、二つ目の観察はほとんど自明です。

命題 7.2 (Prim). \(G\) の最小全域木は全ての安全な辺を含む。

証明 「\(G\) の頂点の任意の部分集合 \(S\) について、\(G\) の最小全域木には端点のちょうど一方が \(S\) に含まれる辺のうち重みが最小のものが含まれる」というより強い命題を示す: 命題 7.1と同じように、貪欲な交換の議論を使ってこの命題を示す。

\(S\) を \(G\) の頂点の任意の部分集合とし、\(e\) を端点のちょうど一方が \(S\) に含まれる \(G\) の辺のうち重みが最小なものとする (辺の重みが全て異なると仮定しているので、\(e\) は曖昧さなく選べる)。\(T\) を \(e\) を含まない任意の \(G\) の全域木とする。これから \(T\) が \(G\) の最小全域木でないことを示す。

\(T\) は連結だから、\(e\) の端点同士を結ぶ路が存在する。この路は \(S\) に含まれる頂点と \(S\) に含まれない頂点を結んでいることから、この路には端点のちょうど一方が \(S\) に含まれる辺が存在する。そのような辺を適当に選んで \(e^{\prime}\) とする。\(T\) は非巡回だから、\(T\) から \(e^{\prime}\) を取り除くと二つの成分を持つ全域森となり、二つの成分は \(e\) の端点を片方ずつ含む。したがってこの森に \(e\) を加えて得られる \(T^{\prime} = T - e^{\prime} + e\) は \(G\) の全域木である。\(e\) の定義から \(w(e^{\prime}) > w(e)\) なので、\(T^{\prime}\) の重みの和は \(T\) よりも小さい。よって \(T\) は \(G\) の最小全域木ではない。 \(\Box\)

全ての安全な辺は最小全域木に含まれる (黒い頂点が部分集合 \(S\) を表す)
図 7.2
全ての安全な辺は最小全域木に含まれる (黒い頂点が部分集合 \(S\) を表す)

命題 7.3 最小全域木は不要な辺を持たない。

証明 \(F\) に不要な辺を加えると閉路ができてしまう。 \(\Box\)

一般的な最小全域木アルゴリズムを一言で言えば「\(F\) に安全な辺を繰り返し加える」です。\(G\) が連結なことから \(F\) が連結でないときには安全な辺が少なくとも一つ存在するので、どのような順番で辺を加えていったとしても \(F\) は最終的に連結となります。よって命題 7.2 から帰納法によって、最終的に出来上がる \(F\) が \(G\) の最小全域木であることが分かります。\(F\) に辺を加えると不定だった辺のいくつかが安全になったり不要になったりする (辺が不要になった場合、その辺はそれ以降ずっと不要です) ので、具体的なアルゴリズムを得るには、各反復でどの安全な辺を加えるのか、そしてどうやって安全な辺を見つけるのかを説明する必要があります。

Borůvka のアルゴリズム

最も古くそしておそらくは最も単純な最小全域木アルゴリズムは、チェコ人数学者 Otakar Borůvka (オタカール・ブルーフカ) によって 1926 年に発見されました。彼がこのアルゴリズムを発見したのは、いくつかの都市を最小の電線で結ぶ電気ネットワークを作るにはどうすればよいかと Jindřich Saxel という人物に尋ねられてから約一年後のことでした2。このアルゴリズムは Gustav Choquet (グスタフ・ショケ) によって 1938 年に、Józef Łukaszewicz (ヨゼフ・ウカセビッチ) を代表とするポーランド人数学者らによって 1951 年に、George Sollin (ジョージ・ソリン) によって 1961 年に再発見されています。Sollin は再発見を公表することはありませんでしたが、このアルゴリズムを詳しく説明したグラフアルゴリズムの最初期の教科書が彼を発見者だとしていたので、このアルゴリズムは "Sollin のアルゴリズム" と呼ばれることがあります。

Borůvka / Choquet / Florek-Łukaziewicz-Perkal-Steinhaus-Zubrzycki / Prim / Sollin / Brosh3 のアルゴリズムは次の一行に要約できます:

Borůvka: 安全な辺をスベテ見つけて再帰する。

例のグラフに対する Borůvka のアルゴリズムの実行例。赤い辺が \(F\) の辺を、破線が不要な辺を、矢印が各成分の安全な辺を表す。実行はたった二回の反復で終了する。
図 7.3
例のグラフに対する Borůvka のアルゴリズムの実行例。赤い辺が \(F\) の辺を、破線が不要な辺を、矢印が各成分の安全な辺を表す。実行はたった二回の反復で終了する。

Borůvka のアルゴリズムの概形を次に示します。このアルゴリズムは 五章で説明した \(\textsc{CountAndLabel}\) アルゴリズムを使っています。\(\textsc{CountAndLabel}\) は \(F\) の各頂点を属する成分の番号を表す \(\mathit{count}(v)\) でラベル付けします。

procedure \(\texttt{Borůvka}\)(\(V, E\))

\(F = (V, \varnothing)\)

\(\mathit{count} \leftarrow\)\(\texttt{CountAndLabel}\)(\(F\))

while \(\mathit{count} > 1\) do

\(\texttt{AddAllSafeEdges}\)(\(E, F, \mathit{count}\))

\(\mathit{count} \leftarrow \)\(\texttt{CountAndLabel}\)(\(F\))

return \(F\)

後は \(F\) の安全な辺を全て見つける方法を説明すれば良いことになります。\(F\) に成分が一つだけならば全域木が手に入っているので、そうでないと仮定します。このとき次に示すサブルーチンは安全な辺 \(\mathit{safe}[1..V]\) を全て見つけます。ここで \(\mathit{safe}[i]\) が端点のちょうど一方が \(F\) の \(i\) 番目の成分に属する辺の中で重みが最小なものを表し、値の計算は \(G\) の辺に対する総当たりによって行われます。各辺 \(uv\) について、\(u\) と \(v\) が同じ成分に属しているなら \(uv\) は不要な辺あるいは \(F\) に含まれる辺なので、何もしません。そうでなければ、\(uv\) の重みと \(\mathit{safe}[\mathit{comp}(u)]\) と \(\mathit{safe}[\mathit{comp}(v)]\) を比べ、必要ならば値を更新します。全ての安全な辺を特定し終えたら、辺 \(\mathit{safe}[i]\) を \(F\) に加えます。

procedure \(\texttt{AddAllSafeEdges}\)(\(E, F, \mathit{count}\))

for \(i \leftarrow 1\) to \(\mathit{count}\) do

\(\mathit{safe}[i] \leftarrow \textsc{Null}\)

for \(uv \in E\) do

if \(\mathit{comp}(u) \neq \mathit{comp}(v)\) then

if \(\mathit{safe}[\mathit{comp}(u)] = \textsc{Null} \text{ or } w(uv) < w(\mathit{safe}[\mathit{comp}(u)])\) then

\(\mathit{safe}[\mathit{comp}(u)] \leftarrow uv\)

if \(\mathit{safe}[\mathit{comp}(v)] = \textsc{Null} \text{ or } w(uv) < w(\mathit{safe}[\mathit{comp}(v)])\) then

\(\mathit{safe}[\mathit{comp}(v)] \leftarrow uv\)

for \(i \leftarrow 1\) to \(\mathit{count}\) do

\(\mathit{safe}[i]\) を \(F\) に加える

\(F\) は最大で \(V-1\) 本の辺を持つので、\(\textsc{CountAndLabel}\) の実行時間は \(O(V)\) です。また \(\textsc{AddAllSafeEdges}\) は \(G\) の各辺と\(F\) の各成分に対して定数時間の処理を行うので、実行時間は \(O(V+E)\) です。入力グラフは連結なことから \(V \leq E + 1\) なので、\(\textsc{Borůvka}\) の while ループ一回分の実行時間は \(O(E)\) だと分かります。

各反復において \(F\) の成分数は少なくとも半分になります ――最悪ケースでは \(F\) の成分が全て組になるからです。\(F\) は最初 \(V\) 個の成分を持つことから、while ループは最大でも \(O(\log V)\) 回反復します。以上より、Borůvka のアルゴリズム全体の実行時間は \(\pmb{O(E \log V)}\) となります。

これこそがあなたの望む MST アルゴリズム

Borůvka のアルゴリズムは誰によって発見されたかが比較的はっきりしなかったにもかかわらず、初期の西洋のアルゴリズム研究者はこのアルゴリズムの存在に気が付いていました。しかし Borůvka アルゴリズムは "複雑すぎる" という理由で忘れられ、結果としてほとんどのアルゴリズムとデータ構造の教科書は単純さと効率の良さを兼ね備えた Borůvka のアルゴリズムに触れることさえしません。これは残念なことであり、重大な誤りです。Borůvka のアルゴリズムは他の古典的なアルゴリズムと比べていくつもの明確な利点があります:

まとめると、もし最小全域木アルゴリズムを実装することになったら、Borůvka のアルゴリズムを使っておけば間違いありません。ただし最小全域木に関する命題を効率良く証明したいなら、次に示す二つのアルゴリズムも知っておく必要があります。

Jarník の (Prim の) アルゴリズム

次に古い最小全域木アルゴリズムはチェコ人数学者 Vojtěch Jarník (ヴォイチェフ・ヤルニク) によって 1925 年に、Borůvka に送った手紙の中で初めて示されました。Jarník は翌年にこの発見を公表しています。同じアルゴリズムは Joseph Kruskal (ジョゼフ・クラスカル) によって 1956 年に、(おそらくは) Robert Prim (ロバート・プリム) によって 1957 年に、Harry Lobermand (ハリー・ロバーマンド) と Arnold Weinberger (アーノルド・ワインバーガー) によって 1957 年に、そして Edsger Dijkstra (エドガー・ダイクストラ) によって 1958 年にそれぞれ独立に再発見されました。Prim, Lobermand, Weinberger, Dijkstra は後に Kruskal の論文のことを知り、引用もしていますが、Kruskal は同じ論文で他に二つの最小全域木アルゴリズムを提案していたので、このアルゴリズムは "Prim のアルゴリズム" あるいは "Prim/Dijkstra のアルゴリズム" と呼ばれることが多いです (1958 年当時 Dijkstra には自分の名前が (事実に反する形で) 付けられた別のアルゴリズムが既にあったのですが)。

Jarník のアルゴリズムでは中間全域森 \(F\) の自明でない成分は一つしか存在せず、他の成分は全て孤立した頂点です。この自明でない成分 \(T\) は最初適当な頂点であり、次に示すステップを \(T\) が全域木になるまで反復します:

Jarník: \(T\) の安全な辺を \(T\) に足す。

Jarník のアルゴリズムの実装では \(T\) に隣接する辺を保持する優先度付きキューを管理します。アルゴリズムの各反復で最小の重みを持つ辺を優先度付きキューからポップし、まずその辺の両端点が \(T\) に入っているかを調べ、もしそうでなければその辺を \(T\) に加え、その頂点に隣接する辺を優先度付きキューにプッシュします。言い換えると、Jarník のアルゴリズムは 五章で説明した "最良優先探索" の一種です！ 優先度付きキューを通常の二分ヒープを使って実装すれば、Jarník のアルゴリズムの実行時間は \(O(E \log E) = \pmb{O(E \log V)}\) となります。

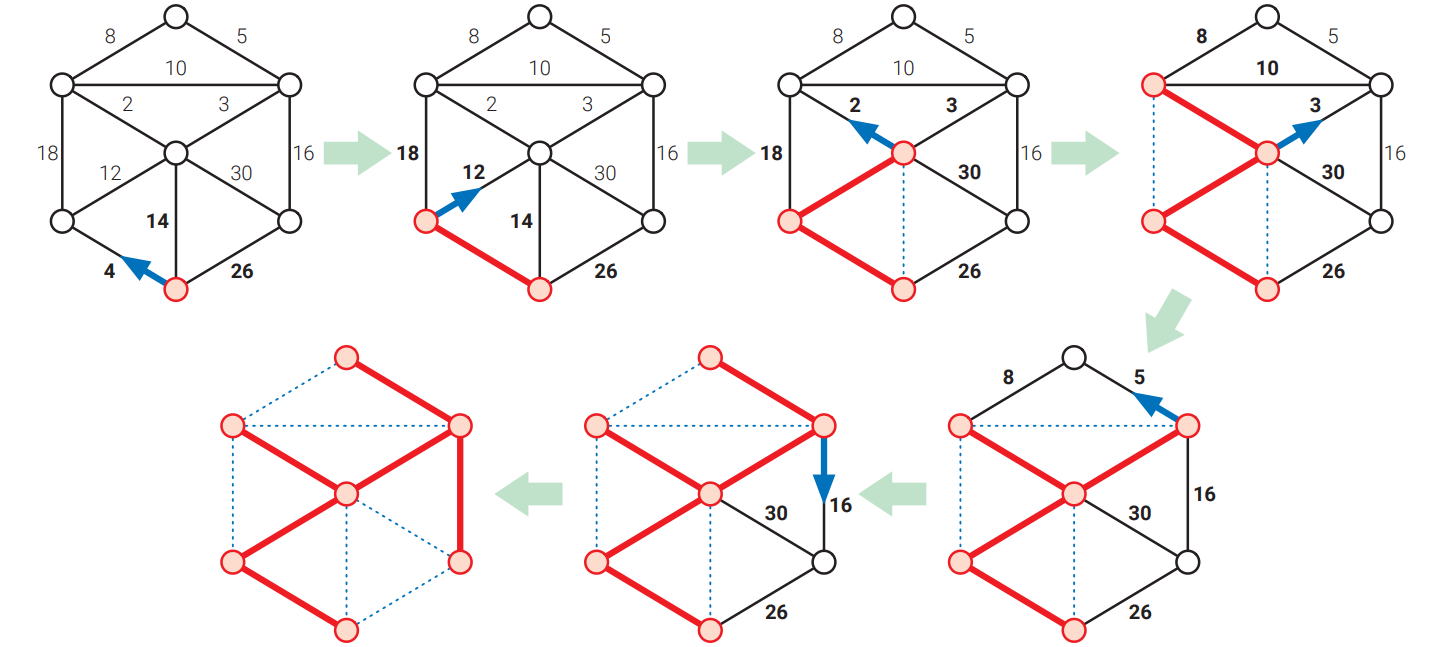
Jarník のアルゴリズムを例のグラフで実行した様子。一番下の頂点から開始している。各ステージにおいて、赤い頂点が \(T\) の頂点を、矢印が \(T\) の安全な辺を、破線が不要な辺を表す。
図 7.4
Jarník のアルゴリズムを例のグラフで実行した様子。一番下の頂点から開始している。各ステージにおいて、赤い頂点が \(T\) の頂点を、矢印が \(T\) の安全な辺を、破線が不要な辺を表す。

❤ Jarník のアルゴリズムの改善

フィボナッチヒープ (fibonacci heap) というより複雑な優先度付きキューのデータ構造を使うと、Jarník のアルゴリズムを改善できます。フィボナッチヒープは Michael Fredman (マイケル・フレッドマン) と Robert Tarjan (ロバート・タージャン) によって 1984 年に提案されました。二分ヒープと同様に、フィボナッチヒープは \(\textsc{Insert}\), \(\textsc{ExtractMin}\), \(\textsc{DecreaseKey}\) の操作をサポートします。しかしこれら全ての操作に \(O(\log n)\) 時間がかかる二分ヒープと違って、フィボナッチヒープは \(\textsc{Insert}\) と \(\textsc{DecreaseKey}\) 操作をならし \(O(1)\) 時間で行えます。ただし \(\textsc{ExtractMin}\) のならし実行時間は \(O(\log n)\) のままです4。

この高速なデータ構造を利用するには、\(G\) の辺ではなく頂点を優先度付きキューに保存する必要があります。ここで頂点 \(v\) の優先度は \(v\) と \(T\) の頂点を結ぶ辺の重みであり、そのような辺が無ければ \(\infty\) です。アルゴリズムの最初で全ての頂点を優先度付きキューに入れておき、\(T\) に新しい辺が加わるたびにその辺に隣接する辺の優先度を小さい値に更新します。

説明を簡単にするために、アルゴリズムを二つに分けます。\(\textsc{JarníkInit}\) が優先度付きキューを初期化し、\(\textsc{JarníkLoop}\) がメインの処理を行います。入力はグラフの頂点と辺、そして開始頂点 \(s\) です。アルゴリズムの実行中、各頂点 \(v\) に対して二つの値が割り当てられます。一つは \(v\) の優先度 \(\mathit{priority}(v)\) で、もう一つは \(w(\mathit{edge}(v)) = \mathit{priority}(v)\) が成り立つような \(v\) に隣接する辺 \(\mathit{edge}(v)\) です。

procedure \(\texttt{Jarník}\)(\(V, E, s\))

\(\texttt{JarníkInit}\)(\(V, E, s\))

\(\texttt{JarníkLoop}\)(\(V, E, s\))

procedure \(\texttt{JarníkInit}\)(\(V, E, s\))

for \(v \in V \backslash \lbrace s \rbrace\) do

if \(vs \in E\) then

\(\mathit{edge}(v) \leftarrow vs\)

\(\mathit{priority}(v) \leftarrow w(vs)\)

else

\(\mathit{edge}(v) \leftarrow \textsc{Null}\)

\(\mathit{priority}(v) \leftarrow \infty\)

\(\texttt{Insert}\)(\(v\))

procedure \(\texttt{JarníkLoop}\)(\(V, E, s\))

\(T \leftarrow (\lbrace s \rbrace, \varnothing)\)

for \(i \leftarrow 1\) to \(|V| - 1\) do

\(v \leftarrow\)\(\texttt{ExtractMin}\)()

\(v\) と \(\mathit{edge}(v)\) を \(T\) に加える

for \(v\) に隣接する頂点 \(u\) do

if \(u \notin T \text{ かつ } \mathit{priority}(u) > w(uv)\) then

\(\mathit{edge}(u) \leftarrow uv\)

\(\texttt{DecreaseKey}\)(\(u, w(uv)\))

図 7.5
フィボナッチヒープを使った Jarník の最小全域木アルゴリズム

\(\textsc{Insert}\) と \(\textsc{ExtractMin}\) は \(s\) 以外の頂点に対して一回ずつ、合計で \(O(V)\) 回呼ばれ、\(\textsc{DecreaseKey}\) は全ての辺に対して最大二回、合計で \(O(E)\) 回呼ばれます。よってフィボナッチヒープを使って改善したアルゴリズムの実行時間は \(\pmb{O(E + V \log V)}\) です。これは \(E = O(V)\) の場合を除いて Borůvka のアルゴリズムよりも高速です。

しかし実際のデータに対してこのアルゴリズムを動かした場合、フィボナッチヒープを使った実装が二分ヒープを使ったナイーブな実装よりも早くなるためには、グラフが極端に巨大かつ密である必要があります。フィボナッチヒープのアルゴリズムはかなり複雑なので、漸近表記に隠されている定数部分が大きいためです ――常軌を逸したほど巨大であるとは言いませんが、二分ヒープの操作の実行時間を表す \(O(\log n)\) という表記に隠れている定数部分よりは明らかに大きいです。

Kruskal のアルゴリズム

最後に紹介する最小全域木アルゴリズムは Joseph Kruskal (ジョセフ・クラスカル) によって 1956 年に、彼が Jarník のアルゴリズムを再発見したのと同じ論文で発表されました。Kruskal がこの論文を書いた動機は、プリンストンの数学部門中を "飛び回って" いた "起源が曖昧な" Borůvka の原著論文の、"タイプライターを使った翻訳" を作ることでした。Kruskal は Borůvka のアルゴリズムを "不必要に難解" だと思っていたようです5。

これまでの最小全域木アルゴリズムと同じように、Kruskal のアルゴリズムにも覚えやすい一行の説明があります:

Kruskal: 重みの昇順に辺を走査し、辺が安全ならば \(F\) に加える。

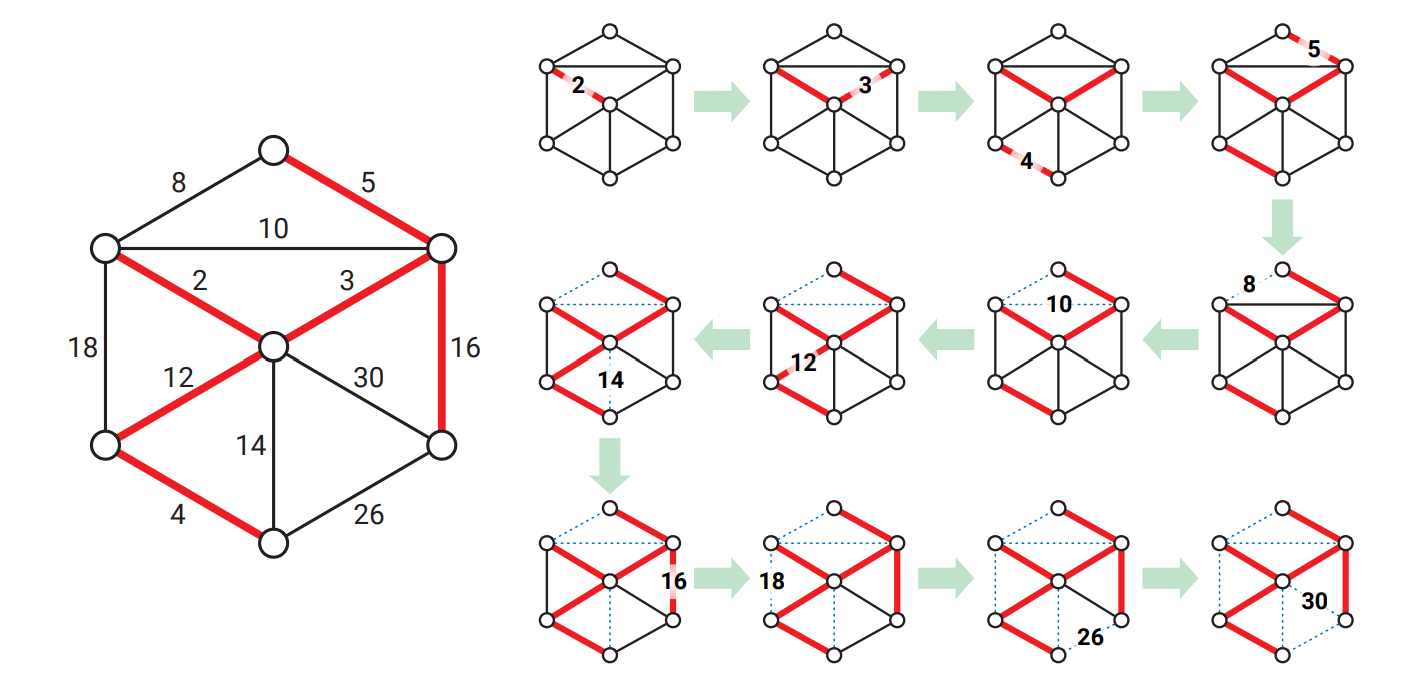
Kruskal のアルゴリズムを例のグラフで実行した様子 (赤い辺が \(F\) を、破線が不要な辺を表す)
図 7.6
Kruskal のアルゴリズムを例のグラフで実行した様子 (赤い辺が \(F\) を、破線が不要な辺を表す)

辺を重みの昇順に走査する一番単純な方法は \(O(E \log E)\) 時間を使って辺を重みでソートしてから for ループを回すことです。これから見るように、この最初のソートがアルゴリズム全体の実行時間を支配します。

辺を軽いものから重いものに向かって見て行っているので、辺が安全かどうかはその辺の端点が森 \(F\) の異なる成分に属しているかどうかと同値です。もし二つの異なる成分 \(A, B\) を結んでいる辺 \(e\) が安全でない場合、\(e\) より軽い辺 \(e^{\prime}\) であって端点のちょうど一方が \(A\) に属するものが存在します。しかし \(F\) に属する \(e\) よりも軽い辺は \(e\) よりも前に調べられていて、かつ安全でないと判定されている (ことが帰納的に分かる) のでこれはあり得ません。

Borůvka のアルゴリズムと同じように、\(F\) の各頂点は自分がどの成分に属しているかを "知っておく" 必要があります。しかし Borůvka のアルゴリズムと違って、Kruskal のアルゴリズムでは辺を追加するたびに成分のラベルを全て再計算する必要はありません。その代わり、二つの成分が辺で結ばれたときに、小さい方の成分に対する何か優先探索を行って頂点のラベルを大きい方の成分のラベルに変更すれば済みます。この探索では小さい成分の各頂点に対して \(O(1)\) 時間の処理が行われます。さらにある頂点を含む成分のラベルが書き換わるにはときにはその頂点を含む成分の大きさが少なくとも二倍になるので、ある頂点のラベルの書き換えは \(O(\log V)\) 回行われます。よって頂点のラベルを更新するために使われる時間は合計で \(O(V\log V)\) です。

より一般的に言うと、Kruskal のアルゴリズムは \(G\) の頂点の互いに重ならない部分集合 (disjoint-set) への分割 (つまり、\(F\) の成分) を管理し、このとき以下の操作をサポートするデータ構造を使います:

これらの操作を使った Kruskal のアルゴリズムの実装を次に示します:

procedure \(\texttt{Kruskal}\)(\(V, E\))

\(E\) を重みで昇順にソートする

\(F \leftarrow (V, \varnothing)\)

for \(v \in V\) do

\(\texttt{MakeSet}\)(\(v\))

for \(i \leftarrow 1\) to \(|E|\) do

\(uv \leftarrow E\) で \(i\) 番目に軽い辺

if \(\texttt{Find}\)(\(u\)) \(\neq\)\(\texttt{Find}\)(\(v\)) then

\(\texttt{Union}\)(\(u, v\))

\(uv\) を \(F\) に追加する

return \(F\)

最初のソートの後、このアルゴリズムはちょうど \(V\) 回 (頂点ごと) の \(\textsc{MakeSet}\)、 \(2E\) 回 (各辺につき二回ずつ) の \(\textsc{Find}\)、\(V-1\) 回 (最小全域木の辺につき一回ずつ) の \(\textsc{Union}\) 操作を行います。先述のフィボナッチヒープは \(\textsc{MakeSet}\) と \(\textsc{Find}\) を \(O(1)\) 時間で、\(\textsc{Union}\) を \(O(\log V)\) のならし時間で行えます。よってこの実装では、集合の分割を管理するために費やされる合計時間は \(O(E+V\log V)\) です6。

しかし思い出してほしいですが、辺をソートするだけで \(O(E\log E) = O(E\log V)\) 時間が必要でした。この時間は \(\textsc{Union-Find}\) データ構造を管理するための時間よりも大きいことから、Kruskal のアルゴリズム全体の実行時間は \(\pmb{O(E \log V)}\) です。これは Borůvka のアルゴリズムおよび通常の (フィボナッチでない) ヒープを使った Jarník のアルゴリズムと変わりません。

練習問題

  1. \(G = (V, E)\) を辺に重みの付いた任意の接続グラフとします。

    1. \(G\) の任意の閉路に対して、\(G\) の最小全域木がその閉路で最大の重みを持つ辺を含まないことを示してください。

    2. 証明または反証してください:「\(G\) の任意の閉路に対して、\(G\) の最小全域木にはその閉路で最小の重みを持つ辺が含まれる」

  2. この章では入力グラフの辺が同じ重みを持たないと仮定し、これによって最小全域木の唯一性を保証してきました。実は、より弱い条件を使っても MST の唯一性を保証できます。

    1. 二つの辺が同じ重みを持っているにもかかわらず最小全域木を一つだけ持つ、辺に重みの付いたグラフを示してください。

    2. 辺に重みの付いたグラフ \(G\) が唯一の最小全域木を持つのは次の条件をどちらも満たす場合に限ることを示してください:

      • 任意の方法で \(G\) の頂点集合を二つに分割したとき、端点が両方の集合に含まれる辺の中で重みが最小なものは唯一である。

      • \(G\) の任意の閉路において、最大の重みを持つ辺は唯一である。

    3. グラフの最小全域木が唯一であるかどうかを判定するアルゴリズムを説明、解析してください。

  3. 多くの古典的な最小全域木アルゴリズムはこの章で説明した "安全" な辺と "不要" な辺という表現を使っていますが、他の定式化もあります。\(G\) を辺に重みの付いた無向グラフとし、辺の重みは全て異なっているとします。ある辺が危険 (dangerous) とはその辺が \(G\) のある閉路で最大の重みを持つことを言い、ある辺が有用 (useful) とはその辺が \(G\) のどの閉路にも含まれていないことを言います。

    1. \(G\) の最小全域木が有用な辺を全て含むことを示してください。

    2. \(G\) の最小全域木が危険な辺を含まないことを示してください。

    3. 次に示すアルゴリズムの効率の良い実装を説明、解析してください。このアルゴリズムは Joseph Kruskal が "Kruskal のアルゴリズム" を提案した 1956 年の論文で初めて示されました。 [ヒント: 通常の Kruskal のアルゴリズムほどは速くありません。]

      「\(G\) の辺を重みの降順で見て行って、もし辺が危険ならば \(G\) から取り除く」

    1. 辺に重みの付いたグラフが与えられたときに、その最大重み全域木を計算するアルゴリズムを説明、解析してください。

    2. 無向グラフ \(G\) のフィードバック辺集合 (feedback edge set) とは、\(G\) の辺の部分集合 \(F\) であって \(G\) の全ての閉路の少なくとも一つの辺が \(F\) に含まれるもの、言い換えると、\(G\) から \(F\) に含まれる辺を取り除くと非巡回グラフが手に入るものを言います。辺に重みの付いたグラフが与えられたときに、最小の重みを持つフィードバック辺集合を高速に計算するアルゴリズムを説明、解析してください。

  5. 辺に重みの付いた無向グラフ \(G\) と \(G\) の最小全域木 \(T\) が与えられたとします。

    1. ある辺 \(e\) の重みが小さくなった場合に、最小全域木を更新するアルゴリズムを説明してください。

    2. ある辺 \(e\) の重みが大きくなった場合に、最小全域木を更新するアルゴリズムを説明してください。

    両方の問題において入力は辺 \(e\) と新しい重みであり、アルゴリズムは \(e\) の重みが変更された後の最小全域木となるように \(T\) を変更します。 [ヒント: \(e \in T\) の場合と \(e \notin T\) の場合を別に考えてください。]

    1. 辺に重みの付いた無向グラフ \(G\) が与えられたときに、\(G\) の二番目に小さい全域木を求めるアルゴリズムを説明、解析してください。つまり、\(G\) の全域木であって最小全域木を除いたときに一番小さいものです。

    2. ❤ 辺に重みの付いた無向グラフ \(G\) と整数 \(k\) が与えられたときに、\(G\) の全域木を小さい方から \(k\) 個計算するアルゴリズムを説明、解析してください。

  7. グラフ \(G=(V, E)\) が \(E = \Theta(V^{2})\) を満たすとき、密 (dense) であると言います。入力のグラフが密なときに実行時間が \(O(V^{2})\) (\(E\) に依存しない) になるように Jarník のアルゴリズムを変更してください。単純なデータ構造だけを使ってください (特に、フィボナッチヒープを使わないでください)。この Jarník のアルゴリズムの変種は 1958 年に Edsger Dijkstra によって初めて発見されました。

  8. 最小全域木アルゴリズムは辺の縮約 (edge contraction) と呼ばれる操作を使って定式化されることもあります。辺 \(uv\) を縮約すると、新しい頂点が追加され、\(u, v\) に隣接する全ての (\(uv\) を除く) 辺が新しい頂点に行くようになり、\(u\) と \(v\) は削除されます。縮約が起こると新しい頂点と他の頂点を結ぶ複数の並列辺が生じることがありますが、この場合は一番軽い辺だけを残してそれ以外を削除します。

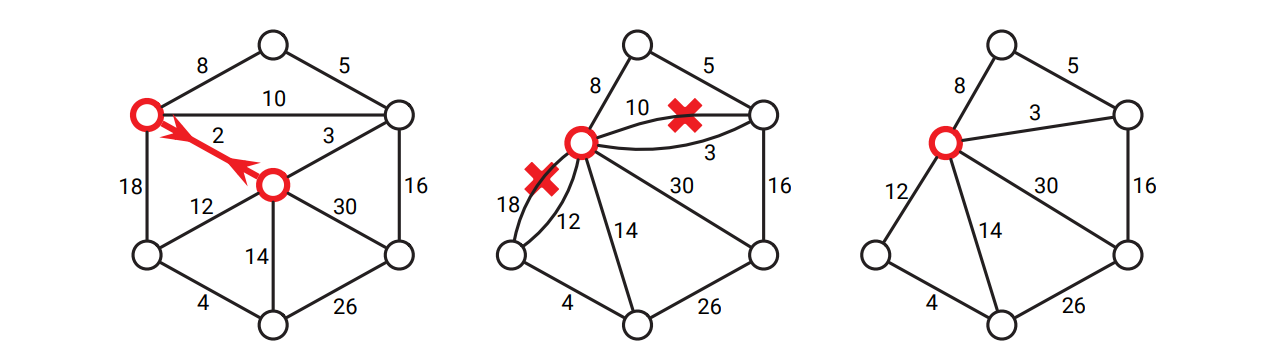    辺を縮約して余分な並列辺を削除する
    図 7.7
    辺を縮約して余分な並列辺を削除する

    この章で説明した三つの古典的アルゴリズムは全て、縮約を使って次のように簡潔に表現できます。三つのアルゴリズムは最初に入力グラフ \(G\) のコピー \(G^{\prime}\) を作ってから処理を開始し、\(G^{\prime}\) の安全な辺を繰り返し縮約していきます。最小全域木は縮約された辺全体からなります。

    • Borůvka: 全ての頂点から出る一番軽い辺に印を付け、印を付けた辺を全て縮約し、再帰する。

    • Jarník: 根となる頂点を適当に選び、隣接する辺で一番軽いものを繰り返し縮約する。

    • Kruskal: グラフの中で一番軽い辺を繰り返し縮約する。

    これらの縮約アルゴリズムに対する問に答えてください:

    1. Borůvka の縮約アルゴリズムの一反復を \(O(V+E)\) 時間で実行する実装を説明してください。入力のグラフは隣接リストで表されているとします。

    2. 最初に Borůvka の縮約アルゴリズムを \(k\) 反復行い、その後縮約されたグラフに対して (フィボナッチヒープを使った) Jarník のアルゴリズムを使うアルゴリズムを考えます。

      1. このハイブリッドなアルゴリズムの実行時間は \(V, E, k\) の関数としていくつですか？

      2. \(k\) がどの値のときに実行時間は最小となりますか？ そのときの実行時間はいくつですか？

    3. 次の特徴を持つグラフの族を素敵 (nice) と呼ぶことにします:

      • \(n\) 頂点の素敵なグラフには辺が \(O(n)\) 個しかない。

      • 素敵なグラフの任意の辺を縮約すると、別の素敵なグラフが手に入る。

      例えば平面グラフ ――平面上に辺を交差させずに書くことができるグラフ―― は素敵です。なぜなら Euler の定理により任意の \(V\) 頂点の平面グラフは最大でも \(3V - 6\) 個の辺しか持たず、平面グラフを縮約するとより小さな平面グラフとなるためです。

      Borůvka の縮約アルゴリズムが素敵なグラフの最小全域木を \(O(V)\) 時間で計算することを示してください。

  9. 辺に重みの付いた無向グラフを \(G\) として、二つの頂点 \(s, t\) の間の路を考えます。路に含まれる辺の重みの最小値は幅と呼ばれます。\(s\) と \(t\) のボトルネック距離とは \(s\) と \(t\) を結ぶ最幅路の幅です (\(s\) と \(t\) を結ぶ路が無いならボトルネック距離は \(-\infty\) であり、\(s\) と \(s\) のボトルネック距離は \(\infty\) です)。

    1. \(G\) の最大全域木が任意の頂点の組に対する最幅路を含んでいることを示してください。

    2. 次の問題を \(O(V+E)\) 時間で解くアルゴリズムを説明してください:「辺に重みの付いた無向グラフ \(G\) とその二つの頂点 \(s, t\) と重み \(W\) が与えられたとき、\(s\) と \(t\) の間のボトルネック距離は \(W\) 以下かを判定する」

    3. \(s\) と \(t\) の間のボトルネック距離が \(B\) だとします。

      1. 重みが \(B\) よりも小さい任意の辺を取り除いても \(s\) と \(t\) の間のボトルネック距離が変化しないことを示してください。

      2. 重みが \(B\) よりも大きい任意の辺を縮約しても \(s\) と \(t\) の間のボトルネック距離が変化しないことを示してください (縮約によって並列な辺ができた場合、一番重い辺だけを残すとします)。

    4. \(s\) と \(t\) の間のボトルネック距離を計算するアルゴリズムを説明してください。 [ヒント: 重みが中央値である \(G\) の辺を見つけるところから始めてください。]

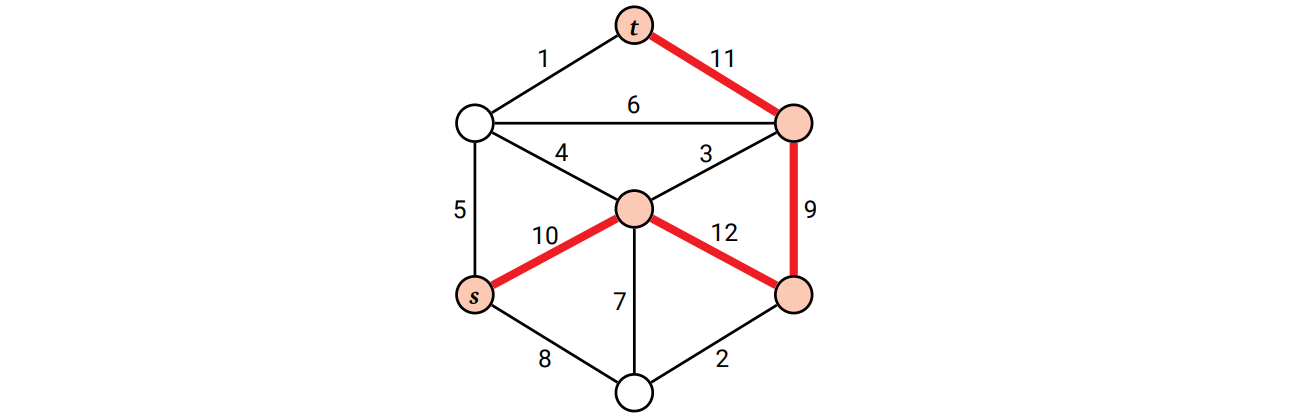    \(s\) と \(t\) のボトルネック距離は 9

  10. Borůvka のアルゴリズムでは各反復において全域森 \(F\) の成分を毎回計算していますが、 Kruskal のアルゴリズムのように標準的な素集合データ構造を使って安全な辺を見つけるようにすることも可能です。

    この変種では \(F\) の各成分が up-tree を使って表されます。つまり各頂点 \(v\) は親へのポインタ \(\mathit{parent}(v)\) を保持します (\(v\) が成分の根ならば \(v = \mathit{parent}(v)\) です)。サブルーチン \(\textsc{Find}(v)\) は \(v\) が属する up-tree の根を返しますが、そのとき根を探す途中に通った中間の頂点の親を根に置き換える、路の圧縮 (path compression) と呼ばれる処理も同時に行います7。サブルーチン \(\textsc{Union}(u, v)\) は、片方の up-tree の根の親をもう片方の up-tree の根にすることで二つの up-tree を一つにします8:

    procedure \(\texttt{Find}\)(\(v\))

    if \(\mathit{parent}(v) = v\) then

    return \(v\)

    else

    \(\overline{v} \leftarrow \textsc{Find}(\mathit{parent}(v))\)

    \(\mathit{parent}(v) \leftarrow \overline{v}\)

    return \(\overline{v}\)

    procedure \(\texttt{Union}\)(\(u, v\))

    \(\overline{u} \leftarrow \textsc{Find}(u)\)

    \(\overline{v} \leftarrow \textsc{Find}(v)\)

    \(\text{either}\)

    \(\quad \mathit{parent}(\overline{u}) \leftarrow \overline{v}\)

    \(\text{or}\)

    \(\quad \mathit{parent}(\overline{v}) \leftarrow \overline{u}\)

    up-tree を使う Borůvka のアルゴリズムの変種を次に示します。\(F\) の各成分は up-tree で表され、各頂点 \(v\) が \(v\) を含む up-tree の親へのポインタ \(\mathit{parent}(v)\) を持ちます。また \(F\) の各成分は (\(\textsc{FindSafeEdges}\) が終了した時点で) \(F\) に端点の片方だけが属する辺の中で一番軽い辺 \(\mathit{safe}(\overline{v})\) も管理します。

    procedure \(\texttt{Borůvka}\)(\(V, E\))

    \(F = \varnothing\)

    for \(v \in V\) do

    \(\mathit{parent}(v) \leftarrow v\)

    while \(\texttt{FindSafeEdges}\)(\(V, E\)) do

    \(\texttt{AddSafeEdges}\)(\(V, E, F\))

    return \(F\)

    procedure \(\texttt{AddSafeEdges}\)(\(V, E, F\))

    for \(v \in V\) do

    if \(\mathit{safe}(v) \neq \textsc{Null}\) then

    \(xy \leftarrow \mathit{safe}(v)\)

    if \(\textsc{Find}(x) \neq \textsc{Find}(y)\) then

    \(\texttt{Union}\)(\(x, y\))

    \(xy\) を \(F\) に加える

    procedure \(\texttt{FindSafeEdges}\)(\(V, E\))

    for \(v \in V\) do

    \(\mathit{safe}(v) \leftarrow \textsc{Null}\)

    \(\mathit{found} \leftarrow \textsc{False}\)

    for \(uv \in E\) do

    \(\overline{u} \leftarrow \textsc{Find}(u);\ \overline{v} \leftarrow \textsc{Find}(v)\)

    if \(\overline{u} \neq \overline{v}\) then

    if \(\mathit{safe}(\overline{u}) = \textsc{Null} \text{ or } w(uv) < w(\mathit{safe}(\overline{u}))\) then

    \(\mathit{safe}(\overline{u}) \leftarrow uv\)

    if \(\mathit{safe}(\overline{v}) = \textsc{Null} \text{ or } w(uv) < w(\mathit{safe}(\overline{v}))\) then

    \(\mathit{safe}(\overline{v}) \leftarrow uv\)

    \(\mathit{found} \leftarrow \textsc{True}\)

    return \(\mathit{found}\)

    \(\textsc{FindSafeEdges}\) と \(\textsc{AddSafeEdges}\) 一回の呼び出しには \(O(E)\) 時間しかかからないことを示してください。これによって \(\textsc{Borůvka}\) が \(O(E \log V)\) で実行できることが分かります。 [ヒント: \(\textsc{FindSafeEdges}\) が終わったときの up-tree の高さはいくつですか？]

  1. この命題の逆は正しくありません。同じ重みの辺を持つ連結グラフでも最小全域木が唯一であることがあります。自明な例として、\(G\) が木の場合を考えてみてください！[return]

  2. Saxel は West Moravian Power Company の従業員であり、Borůvka によると "とても才能のある、良く働く" 人物であったそうです。彼はユダヤ人の家系であったために、後にナチスによって処刑されています。[return]

  3. Hyperbole and a Half を全部読んで、本を買って、猫用にもう一冊買ってください。え？ 猫を飼ってないって？ とんでもない変人ですね。猫を見つけてきて、その猫用に Hyperbole and a Half をもう一冊買ってください。[return]

  4. ならし時間 (amortized time) とはデータ構造の操作において稀に起きる実行時間の変動を無視するための集計上のトリックです。フィボナッチヒープは \(I\) 個の \(\textsc{Insert}\), \(D\) 個の \(\textsc{DecreaseKey}\), \(X\) 個の \(\textsc{ExtractMin}\) を任意に入れ替えた操作列を最悪ケースでも \(O(I+D+X\log n)\) 時間で行えます。ただし、一つ一つの操作の最悪ケースにおける実行時間はこれを平均したものよりも長くなることがあります。 ならし時間の解析で使っているのは操作列の実行時間に対する統計的な平均であり、入力データやアルゴリズムのランダム性は仮定されていません。[return]

  5. 公平のために言っておくと、Borůvka の最初の論文はグラフの言葉ではなくて (線形) 代数の厳密な表記を使って数学者に向けて書かれていたので、確かに不必要に難解でした。同じ 1927 年に Borůvka によって発表された補足論文はずっと広い聴衆に向けて、平易な言葉で、本質的には現在の表記で書かれていましたが、電気工学のジャーナルに発表されていました。そのため Kruskal は Borůvka の二番目の論文について知らなかったと思われます。"鉄のカーテン" とは愚かなことをしたものです。[return]

  6. union-by-rank with path compression と呼ばれる戦略を用いる別の素集合データ構造を使うと、\(\textsc{Union}\) と \(\textsc{Find}\) をならし \(O(\alpha(V))\) 時間で行えます。ここで \(\alpha\) はほとんど定数だが厳密には定数でないことで知られる "アッカーマン関数の逆関数" です。Wikipedia を読む気になれないなら、\(\alpha(V)\) を定数 \(4\) と考えてください。この実装を使うと集合の分割を管理するために費やされる合計時間は \(O(E\alpha(V))\) となり、\(V\) が大きく \(E\) が \(V\) にとても近い場合にはフィボナッチヒープよりも多少高速になります。[return]

  7. 路の圧縮はメモ化の一種です！[return]

  8. 通常 \(\textsc{Union}\) は大きい (もしくは古い) 方の up-tree の根が変わらないように実装されます。しかしここではこの詳細は関係ありません。[return]

広告
このページの文章はテキストゆれないくんを使って校正されました。