練習問題

  1. \(G = (V, E)\) を辺に重みの付いた任意の接続グラフとします。

    1. \(G\) の任意の閉路に対して、\(G\) の最小全域木がその閉路で最大の重みを持つ辺を含まないことを示してください。

    2. 証明または反証してください:「\(G\) の任意の閉路に対して、\(G\) の最小全域木にはその閉路で最小の重みを持つ辺が含まれる」

  2. この章では入力グラフの辺が同じ重みを持たないと仮定し、これによって最小全域木の唯一性を保証してきました。実は、より弱い条件を使っても MST の唯一性を保証できます。

    1. 二つの辺が同じ重みを持っているにもかかわらず最小全域木を一つだけ持つ、辺に重みの付いたグラフを示してください。

    2. 辺に重みの付いたグラフ \(G\) が唯一の最小全域木を持つのは次の条件をどちらも満たす場合に限ることを示してください:

      • 任意の方法で \(G\) の頂点集合を二つに分割したとき、端点が両方の集合に含まれる辺の中で重みが最小なものは唯一である。

      • \(G\) の任意の閉路において、最大の重みを持つ辺は唯一である。

    3. グラフの最小全域木が唯一であるかどうかを判定するアルゴリズムを説明、解析してください。

  3. 多くの古典的な最小全域木アルゴリズムはこの章で説明した "安全" な辺と "不要" な辺という表現を使っていますが、他の定式化もあります。\(G\) を辺に重みの付いた無向グラフとし、辺の重みは全て異なっているとします。ある辺が危険 (dangerous) とはその辺が \(G\) のある閉路で最大の重みを持つことを言い、ある辺が有用 (useful) とはその辺が \(G\) のどの閉路にも含まれていないことを言います。

    1. \(G\) の最小全域木が有用な辺を全て含むことを示してください。

    2. \(G\) の最小全域木が危険な辺を含まないことを示してください。

    3. 次に示すアルゴリズムの効率の良い実装を説明、解析してください。このアルゴリズムは Joseph Kruskal が "Kruskal のアルゴリズム" を提案した 1956 年の論文で初めて示されました。 [ヒント: 通常の Kruskal のアルゴリズムほどは速くありません。]

      「\(G\) の辺を重みの降順で見て行って、もし辺が危険ならば \(G\) から取り除く」

    1. 辺に重みの付いたグラフが与えられたときに、その最大重み全域木を計算するアルゴリズムを説明、解析してください。

    2. 無向グラフ \(G\) のフィードバック辺集合 (feedback edge set) とは、\(G\) の辺の部分集合 \(F\) であって \(G\) の全ての閉路の少なくとも一つの辺が \(F\) に含まれるもの、言い換えると、\(G\) から \(F\) に含まれる辺を取り除くと非巡回グラフが手に入るものを言います。辺に重みの付いたグラフが与えられたときに、最小の重みを持つフィードバック辺集合を高速に計算するアルゴリズムを説明、解析してください。

  5. 辺に重みの付いた無向グラフ \(G\) と \(G\) の最小全域木 \(T\) が与えられたとします。

    1. ある辺 \(e\) の重みが小さくなった場合に、最小全域木を更新するアルゴリズムを説明してください。

    2. ある辺 \(e\) の重みが大きくなった場合に、最小全域木を更新するアルゴリズムを説明してください。

    両方の問題において入力は辺 \(e\) と新しい重みであり、アルゴリズムは \(e\) の重みが変更された後の最小全域木となるように \(T\) を変更します。 [ヒント: \(e \in T\) の場合と \(e \notin T\) の場合を別に考えてください。]

    1. 辺に重みの付いた無向グラフ \(G\) が与えられたときに、\(G\) の二番目に小さい全域木を求めるアルゴリズムを説明、解析してください。つまり、\(G\) の全域木であって最小全域木を除いたときに一番小さいものです。

    2. ❤ 辺に重みの付いた無向グラフ \(G\) と整数 \(k\) が与えられたときに、\(G\) の全域木を小さい方から \(k\) 個計算するアルゴリズムを説明、解析してください。

  7. グラフ \(G=(V, E)\) が \(E = \Theta(V^{2})\) を満たすとき、密 (dense) であると言います。入力のグラフが密なときに実行時間が \(O(V^{2})\) (\(E\) に依存しない) になるように Jarník のアルゴリズムを変更してください。単純なデータ構造だけを使ってください (特に、フィボナッチヒープを使わないでください)。この Jarník のアルゴリズムの変種は 1958 年に Edsger Dijkstra によって初めて発見されました。

  8. 最小全域木アルゴリズムは辺の縮約 (edge contraction) と呼ばれる操作を使って定式化されることもあります。辺 \(uv\) を縮約すると、新しい頂点が追加され、\(u, v\) に隣接する全ての (\(uv\) を除く) 辺が新しい頂点に行くようになり、\(u\) と \(v\) は削除されます。縮約が起こると新しい頂点と他の頂点を結ぶ複数の並列辺が生じることがありますが、この場合は一番軽い辺だけを残してそれ以外を削除します。

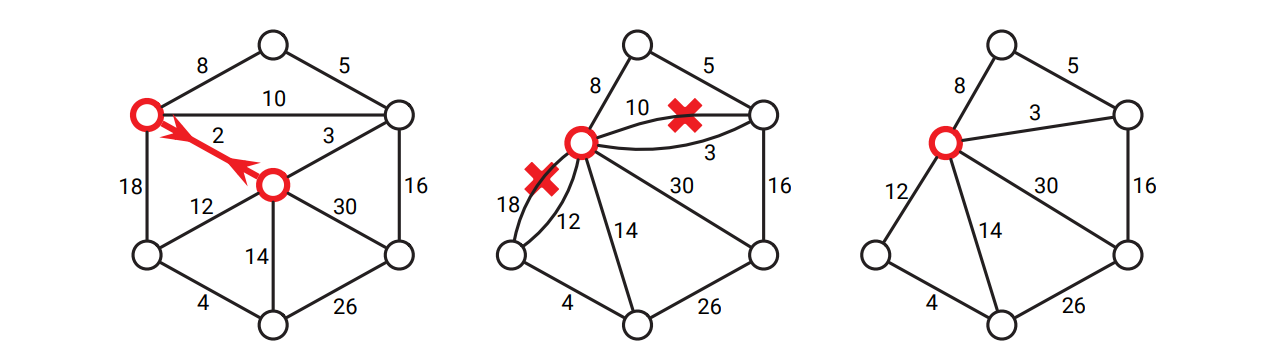    辺を縮約して余分な並列辺を削除する
    図 7.7
    辺を縮約して余分な並列辺を削除する

    この章で説明した三つの古典的アルゴリズムは全て、縮約を使って次のように簡潔に表現できます。三つのアルゴリズムは最初に入力グラフ \(G\) のコピー \(G^{\prime}\) を作ってから処理を開始し、\(G^{\prime}\) の安全な辺を繰り返し縮約していきます。最小全域木は縮約された辺全体からなります。

    • Borůvka: 全ての頂点から出る一番軽い辺に印を付け、印を付けた辺を全て縮約し、再帰する。

    • Jarník: 根となる頂点を適当に選び、隣接する辺で一番軽いものを繰り返し縮約する。

    • Kruskal: グラフの中で一番軽い辺を繰り返し縮約する。

    これらの縮約アルゴリズムに対する問に答えてください:

    1. Borůvka の縮約アルゴリズムの一反復を \(O(V+E)\) 時間で実行する実装を説明してください。入力のグラフは隣接リストで表されているとします。

    2. 最初に Borůvka の縮約アルゴリズムを \(k\) 反復行い、その後縮約されたグラフに対して (フィボナッチヒープを使った) Jarník のアルゴリズムを使うアルゴリズムを考えます。

      1. このハイブリッドなアルゴリズムの実行時間は \(V, E, k\) の関数としていくつですか？

      2. \(k\) がどの値のときに実行時間は最小となりますか？ そのときの実行時間はいくつですか？

    3. 次の特徴を持つグラフの族を素敵 (nice) と呼ぶことにします:

      • \(n\) 頂点の素敵なグラフには辺が \(O(n)\) 個しかない。

      • 素敵なグラフの任意の辺を縮約すると、別の素敵なグラフが手に入る。

      例えば平面グラフ ――平面上に辺を交差させずに書くことができるグラフ―― は素敵です。なぜなら Euler の定理により任意の \(V\) 頂点の平面グラフは最大でも \(3V - 6\) 個の辺しか持たず、平面グラフを縮約するとより小さな平面グラフとなるためです。

      Borůvka の縮約アルゴリズムが素敵なグラフの最小全域木を \(O(V)\) 時間で計算することを示してください。

  9. 辺に重みの付いた無向グラフを \(G\) として、二つの頂点 \(s, t\) の間の路を考えます。路に含まれる辺の重みの最小値は幅と呼ばれます。\(s\) と \(t\) のボトルネック距離とは \(s\) と \(t\) を結ぶ最幅路の幅です (\(s\) と \(t\) を結ぶ路が無いならボトルネック距離は \(-\infty\) であり、\(s\) と \(s\) のボトルネック距離は \(\infty\) です)。

    1. \(G\) の最大全域木が任意の頂点の組に対する最幅路を含んでいることを示してください。

    2. 次の問題を \(O(V+E)\) 時間で解くアルゴリズムを説明してください:「辺に重みの付いた無向グラフ \(G\) とその二つの頂点 \(s, t\) と重み \(W\) が与えられたとき、\(s\) と \(t\) の間のボトルネック距離は \(W\) 以下かを判定する」

    3. \(s\) と \(t\) の間のボトルネック距離が \(B\) だとします。

      1. 重みが \(B\) よりも小さい任意の辺を取り除いても \(s\) と \(t\) の間のボトルネック距離が変化しないことを示してください。

      2. 重みが \(B\) よりも大きい任意の辺を縮約しても \(s\) と \(t\) の間のボトルネック距離が変化しないことを示してください (縮約によって並列な辺ができた場合、一番重い辺だけを残すとします)。

    4. \(s\) と \(t\) の間のボトルネック距離を計算するアルゴリズムを説明してください。 [ヒント: 重みが中央値である \(G\) の辺を見つけるところから始めてください。]

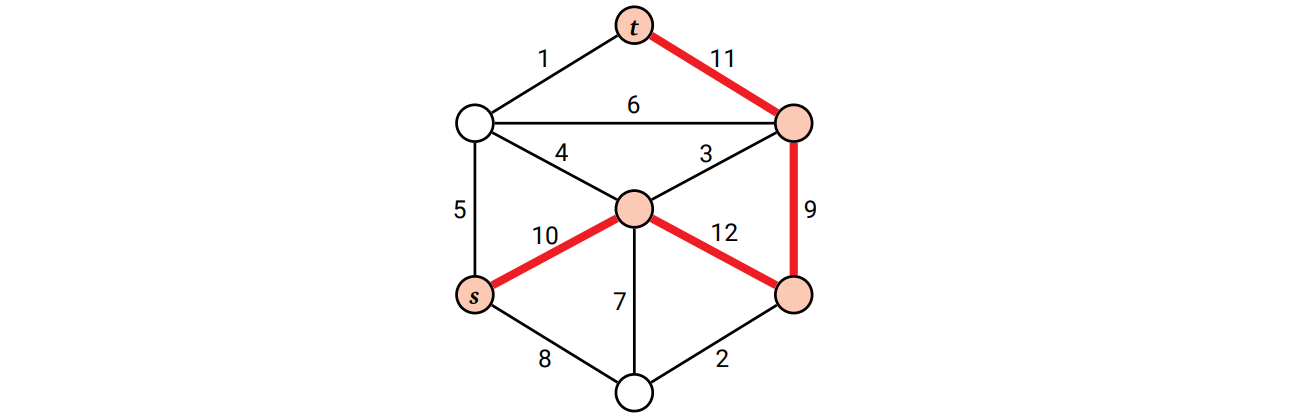    \(s\) と \(t\) のボトルネック距離は 9

  10. Borůvka のアルゴリズムでは各反復において全域森 \(F\) の成分を毎回計算していますが、 Kruskal のアルゴリズムのように標準的な素集合データ構造を使って安全な辺を見つけるようにすることも可能です。

    この変種では \(F\) の各成分が up-tree を使って表されます。つまり各頂点 \(v\) は親へのポインタ \(\mathit{parent}(v)\) を保持します (\(v\) が成分の根ならば \(v = \mathit{parent}(v)\) です)。サブルーチン \(\textsc{Find}(v)\) は \(v\) が属する up-tree の根を返しますが、そのとき根を探す途中に通った中間の頂点の親を根に置き換える、路の圧縮 (path compression) と呼ばれる処理も同時に行います1。サブルーチン \(\textsc{Union}(u, v)\) は、片方の up-tree の根の親をもう片方の up-tree の根にすることで二つの up-tree を一つにします2:

    procedure \(\texttt{Find}\)(\(v\))

    if \(\mathit{parent}(v) = v\) then

    return \(v\)

    else

    \(\overline{v} \leftarrow \textsc{Find}(\mathit{parent}(v))\)

    \(\mathit{parent}(v) \leftarrow \overline{v}\)

    return \(\overline{v}\)

    procedure \(\texttt{Union}\)(\(u, v\))

    \(\overline{u} \leftarrow \textsc{Find}(u)\)

    \(\overline{v} \leftarrow \textsc{Find}(v)\)

    \(\text{either}\)

    \(\quad \mathit{parent}(\overline{u}) \leftarrow \overline{v}\)

    \(\text{or}\)

    \(\quad \mathit{parent}(\overline{v}) \leftarrow \overline{u}\)

    up-tree を使う Borůvka のアルゴリズムの変種を次に示します。\(F\) の各成分は up-tree で表され、各頂点 \(v\) が \(v\) を含む up-tree の親へのポインタ \(\mathit{parent}(v)\) を持ちます。また \(F\) の各成分は (\(\textsc{FindSafeEdges}\) が終了した時点で) \(F\) に端点の片方だけが属する辺の中で一番軽い辺 \(\mathit{safe}(\overline{v})\) も管理します。

    procedure \(\texttt{Borůvka}\)(\(V, E\))

    \(F = \varnothing\)

    for \(v \in V\) do

    \(\mathit{parent}(v) \leftarrow v\)

    while \(\texttt{FindSafeEdges}\)(\(V, E\)) do

    \(\texttt{AddSafeEdges}\)(\(V, E, F\))

    return \(F\)

    procedure \(\texttt{AddSafeEdges}\)(\(V, E, F\))

    for \(v \in V\) do

    if \(\mathit{safe}(v) \neq \textsc{Null}\) then

    \(xy \leftarrow \mathit{safe}(v)\)

    if \(\textsc{Find}(x) \neq \textsc{Find}(y)\) then

    \(\texttt{Union}\)(\(x, y\))

    \(xy\) を \(F\) に加える

    procedure \(\texttt{FindSafeEdges}\)(\(V, E\))

    for \(v \in V\) do

    \(\mathit{safe}(v) \leftarrow \textsc{Null}\)

    \(\mathit{found} \leftarrow \textsc{False}\)

    for \(uv \in E\) do

    \(\overline{u} \leftarrow \textsc{Find}(u);\ \overline{v} \leftarrow \textsc{Find}(v)\)

    if \(\overline{u} \neq \overline{v}\) then

    if \(\mathit{safe}(\overline{u}) = \textsc{Null} \text{ or } w(uv) < w(\mathit{safe}(\overline{u}))\) then

    \(\mathit{safe}(\overline{u}) \leftarrow uv\)

    if \(\mathit{safe}(\overline{v}) = \textsc{Null} \text{ or } w(uv) < w(\mathit{safe}(\overline{v}))\) then

    \(\mathit{safe}(\overline{v}) \leftarrow uv\)

    \(\mathit{found} \leftarrow \textsc{True}\)

    return \(\mathit{found}\)

    \(\textsc{FindSafeEdges}\) と \(\textsc{AddSafeEdges}\) 一回の呼び出しには \(O(E)\) 時間しかかからないことを示してください。これによって \(\textsc{Borůvka}\) が \(O(E \log V)\) で実行できることが分かります。 [ヒント: \(\textsc{FindSafeEdges}\) が終わったときの up-tree の高さはいくつですか？]

  1. 路の圧縮はメモ化の一種です！[return]

  2. 通常 \(\textsc{Union}\) は大きい (もしくは古い) 方の up-tree の根が変わらないように実装されます。しかしここではこの詳細は関係ありません。[return]

広告
このページの文章はテキストゆれないくんを使って校正されました。