Kruskal のアルゴリズム

最後に紹介する最小全域木アルゴリズムは Joseph Kruskal (ジョセフ・クラスカル) によって 1956 年に、彼が Jarník のアルゴリズムを再発見したのと同じ論文で発表されました。Kruskal がこの論文を書いた動機は、プリンストンの数学部門中を "飛び回って" いた "起源が曖昧な" Borůvka の原著論文の、"タイプライターを使った翻訳" を作ることでした。Kruskal は Borůvka のアルゴリズムを "不必要に難解" だと思っていたようです¹。

これまでの最小全域木アルゴリズムと同じように、Kruskal のアルゴリズムにも覚えやすい一行の説明があります:

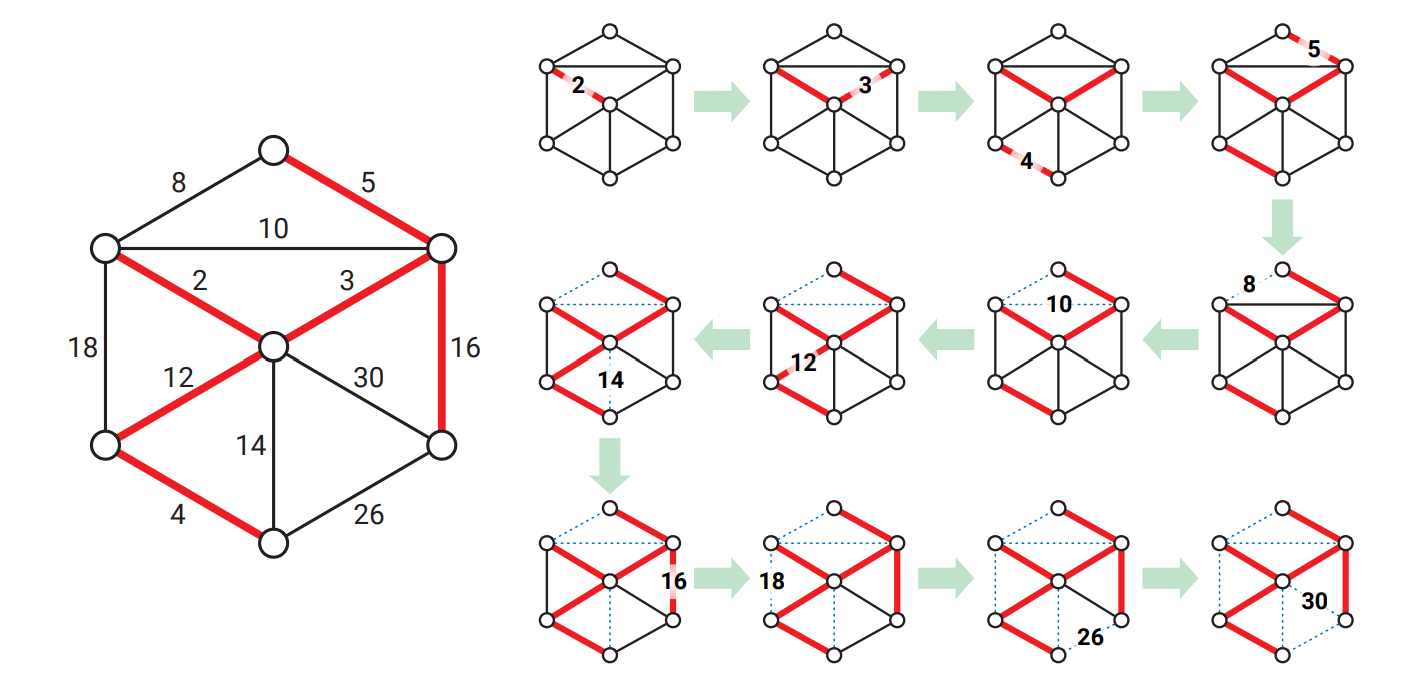
辺を重みの昇順に走査する一番単純な方法は \(O(E \log E)\) 時間を使って辺を重みでソートしてから for ループを回すことです。これから見るように、この最初のソートがアルゴリズム全体の実行時間を支配します。

辺を軽いものから重いものに向かって見て行っているので、辺が安全かどうかはその辺の端点が森 \(F\) の異なる成分に属しているかどうかと同値です。もし二つの異なる成分 \(A, B\) を結んでいる辺 \(e\) が安全でない場合、\(e\) より軽い辺 \(e^{\prime}\) であって端点のちょうど一方が \(A\) に属するものが存在します。しかし \(F\) に属する \(e\) よりも軽い辺は \(e\) よりも前に調べられていて、かつ安全でないと判定されている (ことが帰納的に分かる) のでこれはあり得ません。

Borůvka のアルゴリズムと同じように、\(F\) の各頂点は自分がどの成分に属しているかを "知っておく" 必要があります。しかし Borůvka のアルゴリズムと違って、Kruskal のアルゴリズムでは辺を追加するたびに成分のラベルを全て再計算する必要はありません。その代わり、二つの成分が辺で結ばれたときに、小さい方の成分に対する何か優先探索を行って頂点のラベルを大きい方の成分のラベルに変更すれば済みます。この探索では小さい成分の各頂点に対して \(O(1)\) 時間の処理が行われます。さらにある頂点を含む成分のラベルが書き換わるにはときにはその頂点を含む成分の大きさが少なくとも二倍になるので、ある頂点のラベルの書き換えは \(O(\log V)\) 回行われます。よって頂点のラベルを更新するために使われる時間は合計で \(O(V\log V)\) です。

より一般的に言うと、Kruskal のアルゴリズムは \(G\) の頂点の互いに重ならない部分集合 (disjoint-set) への分割 (つまり、\(F\) の成分) を管理し、このとき以下の操作をサポートするデータ構造を使います:

• \(\textsc{MakeSet}(v)\) ―― 頂点 \(v\) だけを含む集合を作る。
• \(\textsc{Find}(v)\) ―― 頂点 \(v\) を含む集合の識別子を返す。
• \(\textsc{Union}(u, v)\) ―― \(u\) と \(v\) を含む集合をそれらの和集合で置き換える (この操作によって全体の集合の数が減少する)。

これらの操作を使った Kruskal のアルゴリズムの実装を次に示します:

最初のソートの後、このアルゴリズムはちょうど \(V\) 回 (頂点ごと) の \(\textsc{MakeSet}\)、 \(2E\) 回 (各辺につき二回ずつ) の \(\textsc{Find}\)、\(V-1\) 回 (最小全域木の辺につき一回ずつ) の \(\textsc{Union}\) 操作を行います。先述のフィボナッチヒープは \(\textsc{MakeSet}\) と \(\textsc{Find}\) を \(O(1)\) 時間で、\(\textsc{Union}\) を \(O(\log V)\) のならし時間で行えます。よってこの実装では、集合の分割を管理するために費やされる合計時間は \(O(E+V\log V)\) です²。

しかし思い出してほしいですが、辺をソートするだけで \(O(E\log E) = O(E\log V)\) 時間が必要でした。この時間は \(\textsc{Union-Find}\) データ構造を管理するための時間よりも大きいことから、Kruskal のアルゴリズム全体の実行時間は \(\pmb{O(E \log V)}\) です。これは Borůvka のアルゴリズムおよび通常の (フィボナッチでない) ヒープを使った Jarník のアルゴリズムと変わりません。

1. 公平のために言っておくと、Borůvka の最初の論文はグラフの言葉ではなくて (線形) 代数の厳密な表記を使って数学者に向けて書かれていたので、確かに不必要に難解でした。同じ 1927 年に Borůvka によって発表された補足論文はずっと広い聴衆に向けて、平易な言葉で、本質的には現在の表記で書かれていましたが、電気工学のジャーナルに発表されていました。そのため Kruskal は Borůvka の二番目の論文について知らなかったと思われます。"鉄のカーテン" とは愚かなことをしたものです。^[return]

2. union-by-rank with path compression と呼ばれる戦略を用いる別の素集合データ構造を使うと、\(\textsc{Union}\) と \(\textsc{Find}\) をならし \(O(\alpha(V))\) 時間で行えます。ここで \(\alpha\) はほとんど定数だが厳密には定数でないことで知られる "アッカーマン関数の逆関数" です。Wikipedia を読む気になれないなら、\(\alpha(V)\) を定数 \(4\) と考えてください。この実装を使うと集合の分割を管理するために費やされる合計時間は \(O(E\alpha(V))\) となり、\(V\) が大きく \(E\) が \(V\) にとても近い場合にはフィボナッチヒープよりも多少高速になります。^[return]