3 SAT (CircuitSAT からの帰着)

様々な問題の NP 困難性を証明するのに特に便利な \(\textsc{SAT}\) の特殊ケースがあり、\(\textsc{3CNF-SAT}\) あるいは \(\textsc{3SAT}\) と呼ばれます。

ブール式が連言標準形 (conjunctive normal form, CNF) であるとは、式がいくつかの節 (clause) の連言 (disjunction, \(\textsc{Or}\)) であり、それぞれの節がリテラルの選言からなる (conjunction, \(\textsc{And}\)) ことを言います。ここでリテラルは一つの変数またはその否定です。例えば: \[ \overbrace{(a \lor b \lor c \lor d)}^{\text{節 (clause)}} \land (b \lor \overline{c} \lor \overline{d}) \land (\overline{a} \lor c \lor d) \land (a \lor \overline{b}) \] は CNF 式です。3CNF 式とは 全ての節が三つのリテラルからなる CNF 式のことです。上の式では最初の節にはリテラルが 4 つ、最後の節にはリテラルが 2 つあるので 3SAT ではありません。3CNF 式が与えられたときに、その式が \(\textsc{True}\) に評価されるような変数への真偽値割り当ては存在するでしょうか？

\(\textsc{3SAT}\) を一般的な \(\textsc{SAT}\) からの帰着で示すこともできますが、\(\textsc{CircuitSAT}\) からの帰着を作って "最初から" 示した方が簡単です。

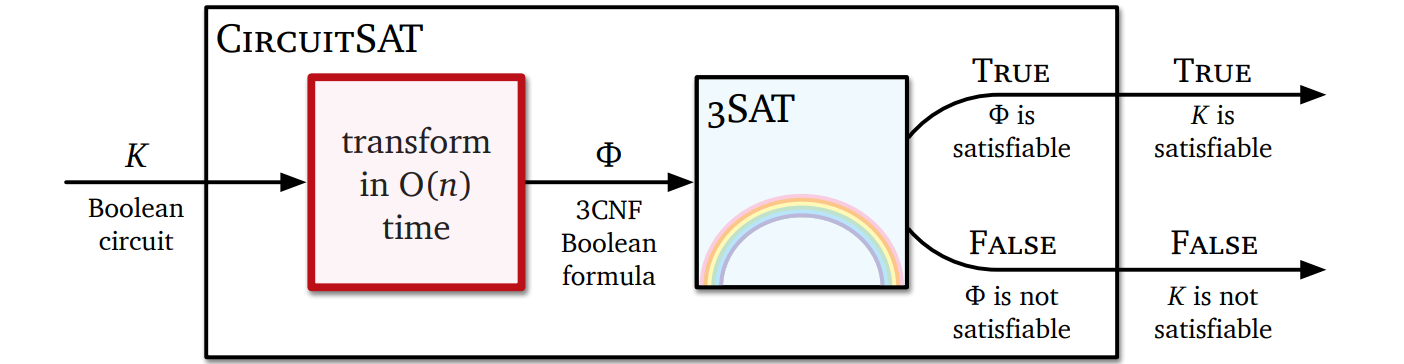
任意のブール回路 \(K\) が与えられたとき、次に示すステージを経ることで \(K\) を同値な 3CNF 式に変換できます。各ステージを説明すると同時にその正しさの証明も行います。

• \(K\) が \(k > 2\) 個の入力を持つゲートがある場合には、そのゲートを \(k - 1\) 個のゲートからなる二分木に置き換えることで、全ての \(\textsc{And}\) ゲートと \(\textsc{Or}\) ゲートの入力の数を二つにする。置き換えた後の回路を \(K^{\prime}\) とすると、\(K\) と \(K^{\prime}\) は論理的に同値な回路だから、\(K\) を充足させる入力は \(K^{\prime}\) も充足させ、その逆も成り立つ。

• 前節で \(\textsc{SAT}\) の帰着に用いたのと同じ方法を使って、各ゲートが一つの節に対応するように \(K^{\prime}\) をブール式 \(\Phi_{1}\) に変形する。\(K^{\prime}\) を充足させる入力は \(\Phi_{1}\) を充足させる入力に変換できることおよびその逆は前に示した。

• \(\Phi_{1}\) に含まれる全ての節を CNF 式に置き換える。\(\Phi_{1}\) が持つ節の形は \(K^{\prime}\) のゲートの種類に対応して三種類だけであり、それぞれ次のように変換できる: \[ \begin{aligned} a = b \land c & \longmapsto (a \lor \overline{b} \lor \overline{c}) \land (\overline{a} \lor b) \land (\overline{a} \lor c) \\ a = b \lor c & \longmapsto (\overline{a} \lor b \lor c) \land (a \lor \overline{b}) \land (a \lor \overline{c}) \\ a = \overline{b} & \longmapsto (a \lor b) \land (\overline{a} \lor \overline{b}) \end{aligned} \] こうして出来上がる CNF 式を \(\Phi_{2}\) とする。\(\Phi_{1}\) と \(\Phi_{2}\) は論理的に同値な式だから、\(\Phi_{1}\) を充足させる入力は \(\Phi_{2}\) も充足させ、その逆も成り立つ¹。

• \(\Phi_{2}\) の各節を 3CNF 式に置き換える。\(\Phi_{2}\) の各節は最大でも三つのリテラルを持つので、三つのリテラルを持つ節はそのままにし、それ以外の二種類の節は次のように展開する。展開のときには新しい変数が導入される: \[ \begin{aligned} a \lor b & \longmapsto (a \lor b \lor x) \land (a \lor b \lor \overline{x}) \\ a & \longmapsto (a \lor y \lor x) \land (a \lor \overline{y} \lor x) \land (a \lor y \lor \overline{x}) \land (a \lor \overline{y} \lor \overline{x}) \end{aligned} \] 最終的に出来上がる 3CNF 式を \(\Phi_{3}\) とする。\(\Phi_{2}\) を充足させる任意の入力は、新しい変数 (\(x\) と \(y\)) にどんな値を割り当てても \(\Phi_{3}\) を充足させる入力となる。逆に \(\Phi_{3}\) を充足させる任意の入力の新しい変数を無視すると \(\Phi_{2}\) を充足させる入力となる。

例えば例として出した回路は次の 3CNF 式となります: \[ \begin{aligned} & (y_1 ∨ x_1 ∨ x_4) ∧ (y_1 ∨ x_1 ∨ z_1) ∧ (y_1 ∨ x_1 ∨ z_1) ∧ (y_1 ∨ x_4 ∨ z_2) ∧ {} \\ & (y_1 ∨ x_4 ∨ z_2) ∧ (y_2 ∨ x_4 ∨ z_3) ∧ (y_2 ∨ x_4 ∨ z_3) ∧ (y_2 ∨ x_4 ∨ z_4) ∧ {} \\ & (y_2 ∨ x_4 ∨ z_4)∧ (y_3 ∨ x_3 ∨ y_2) ∧ (y_3 ∨ x_3 ∨ z_5) ∧ (y_3 ∨ x_3 ∨ z_5) ∧ {} \\ & (y_3 ∨ y_2 ∨ z_6) ∧ (y_3 ∨ y_2 ∨ z_6) ∧ (y_4 ∨ y_1 ∨ x_2) ∧ (y_4 ∨ x_2 ∨ z_7) ∧ {} \\ & (y_4 ∨ x_2 ∨ z_7) ∧ (y_4 ∨ y_1 ∨ z_8) ∧ (y_4 ∨ y_1 ∨ z_8) ∧ (y_5 ∨ x_2 ∨ z_9) ∧ {} \\ & (y_5 ∨ x_2 ∨ z_9) ∧ (y_5 ∨ x_2 ∨ z_{10}) ∧ (y_5 ∨ x_2 ∨ z_{10}) ∧ (y_6 ∨ x_5 ∨ z_{11}) ∧ {} \\ & (y_6 ∨ x_5 ∨ z_{11}) ∧ (y_6 ∨ x_5 ∨ z_{12}) ∧ (y_6 ∨ x_5 ∨ z_{12}) ∧ (y_7 ∨ y_3 ∨ y_5) ∧ {} \\ & (y_7 ∨ y_3 ∨ z_{13}) ∧ (y_7 ∨ y_3 ∨ z_{13}) ∧ (y_7 ∨ y_5 ∨ z_{14}) ∧ (y_7 ∨ y_5 ∨ z_{14}) ∧ {} \\ & (y_8 ∨ y_4 ∨ y_7) ∧ (y_8 ∨ y_4 ∨ z_{15}) ∧ (y_8 ∨ y_4 ∨ z_{15}) ∧ (y_8 ∨ y_7 ∨ z_{16}) ∧ {} \\ & (y_8 ∨ y_7 ∨ z_{16}) ∧ (y_9 ∨ y_8 ∨ y_6) ∧ (y_9 ∨ y_8 ∨ z_{17}) ∧ (y_9 ∨ y_6 ∨ z_{18}) ∧ {} \\ & (y_9 ∨ y_6 ∨ z_{18}) ∧ (y_9 ∨ y_8 ∨ z_{17}) ∧ (y_9 ∨ z_{19} ∨ z_{20}) ∧ (y_9 ∨ z_{19} ∨ z_{20}) ∧ {} \\ & (y_9 ∨ z_{19} ∨ z_{20}) ∧ (y_9 ∨ z_{19} ∨ z_{20}) \end{aligned} \]

この式は一見すると元の回路よりもはるかに複雑に見えますが、各ゲートが最大でも五つの節に変換されることから分かるように、実際には定数倍しか大きくありません。回路の大きさに対する式の大きさが (\(n^{374}\) のような) 次数の大きな多項式になったとしても、NP 困難性を示すための帰着としては何ら不都合はありません。

以上の帰着によって、任意のブール回路 \(K\) は多項式時間で 3CNF 式 \(\Phi_{3}\) に変換できます。また \(K\) を充足させる任意の入力は \(\Phi_{3}\) を充足させる入力に変換でき、その逆も行えます。言い換えれば「\(K\) が充足可能 \(\iff\) \(\Phi_{3}\) が充足可能」ということです。よってもし \(\textsc{3SAT}\) が多項式時間で解けるならば \(\textsc{CircuitSAT}\) も多項式時間で解くことができ、P=NP です。以上より、\(\textsc{3SAT}\) が NP 困難であると結論できます。

1. 各節のリテラルが最大でも三つであるような連言標準形 \(\Phi_{2}\) を使ってブール回路 \(K\) を表すためのこの方法は、1966 年に Grigorii Tseitin (グリゴリイ・セイティン) によって示されています。 1966 年というのは Levin が prebor problems に対する結果を公表する五年前です。同じ論文で Tseitin は、私たちが現在 \(\textsc{CNF-SAT}\) と呼ぶ問題をおそらく世界で初めて定義しています。^[return]