ちょっとした現実世界の例
ドラフツ (draughts) は何千年にもわたって遊ばれているボードゲームです。ドラフツには様々なバージョンがありますが、アメリカ人の多くにとってはチェッカー (checker) あるいはイングリッシュドラフツ (English draughts) と呼ばれるものが一番身近でしょう。しかし世界で一番知られているバージョンは国際ドラフツ (international draughts) あるいはポーランドドラフツ (Polish draughts) と呼ばれるものであり、16 世紀のオランダに起源を持ちます。完全なルールについては Wikipedia に譲り、英米バージョンとの主な違いをここに示します:
-
空飛ぶキング: チェッカーと同じように、相手の陣地の一番奥まで進んだ駒はキングになり、後ろに進むことができるようになる。ただしチェッカーと異なり、キングは斜め方向にいくらでも進むことができる。キングは相手の駒を一つだけ飛び越して移動でき、飛び越された相手の駒は盤から取り除かれる。
-
必ず最も多く取る: それぞれのターンにおいて、プレイヤーは取り除かれる相手の駒の数が最大になるように駒を動かさなければならない。通常のチェッカーには駒を動かした後にさらに駒を取れるなら必ず動かすというルールがあるが、国際ドラフツのルールはこれと異なる。つまり、チェッカーでは取り除かれる駒の数が必ず極大値となるのに対して、国際ドラフツでは取り除かれる駒の数が必ず全ての手の中の最大値となる。
-
駒を取り除くときの動作: チェッカーと同じように、駒が取り除かれるのはターンの終わりである。一つの駒が取り除かれるのは一回だけなので、一度飛び越された駒はそのターンの終わりまで飛び越すことができない障害物として盤に残る。
例えば次に示す初期状態において円が普通の駒を、二重の円がキングを表しているとすると、黒は必ず図に示された動きを行わなければなりません。この動きで黒が取り除くことになる白い駒の数 \(5\) が他のどんな動きよりも多いからです。黒の駒が 5 個の駒を取った後に動きをこれ以上続けられないのは、一度取った駒はターンが終わるまで盤に残ったままであるためです。その後白は図に示された動きを必ず行わなければならず、この動きによって白が勝利します。
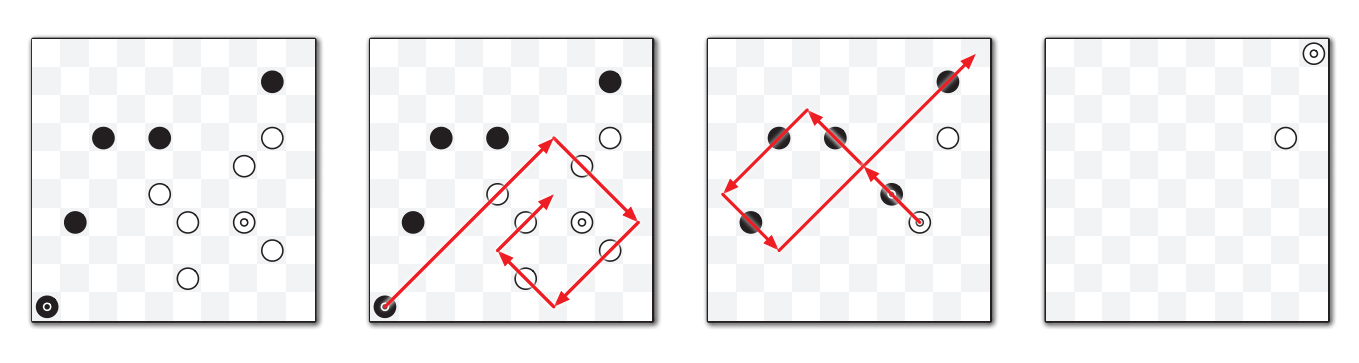
実際のゲームは \(10 \times 10\) の盤と双方 20 個ずつの駒を使って行いますが、この設定では任意のゲームが計算機的に自明になってしまいます。つまり、任意の盤面に対する可能な手をあらかじめ計算して定数サイズのルックアップテーブルに格納しておくことで、次の盤面の計算が定数時間で行えるということです。もちろん定数は巨大になりますが、定数であることに違いはありません!
しかし国際ドラフツを \(n \times n\) に自然に拡張した場合、合法な手を見つけることが NP 困難になります! 次に説明するのは 2010 年に Bob Hearn によって発見された1 有向グラフにおけるハミルトン閉路問題からの帰着です。ほとんどの二人対戦ゲームにおいては最良の手を見つける問題が NP 困難に (あるいはそれ以上に難しく) なりますが、ルールに従うだけで NP 困難となってしまうゲーム ――さらに言えば、何世紀にもわたって遊ばれているゲーム―― というのは私はこれしか知りません!
\(n\) 頂点の無向グラフ \(G\) が与えられたと仮定して、国際ドラフツの盤面であって \(G\) にハミルトン閉路が存在するときに限って白が指定された数の黒の駒を取れるものをこれから構築します。\(G\) の頂点に適当な順番で \(1\) から \(n\) まで番号を振り、\(G\) の無向辺 \(uv\) を \(u \rightarrow v\) と \(v \rightarrow u\) に分けることで \(G\) を有向グラフとして考えます。構築するドラフツの盤面はいくつかのガジェットからなります:
-
\(G\) の頂点はウサギの顔の形をした頂点ガジェットで表される。頂点ガジェットは水平に一列に並び、各辺 \(i \rightarrow j\) は頂点ガジェット \(i\) の "右耳" と頂点ガジェット \(j\) の "左耳" を結ぶ直角に交わる二つの線分で表される。弧 \(i \rightarrow j\) は \(i < j\) ならば頂点ガジェットの上に、\(i > j\) ならば頂点ガジェットの下に引かれる。
-
頂点ガジェットの下半分はダイアモンドの形をした "金庫" である。金庫には図中で灰色の円で示されている壁があり、二つの黒い駒の層からなっているので飛び越えることができない。金庫の中には \(N\) 個の黒い駒があり、白のキングは一度に全てを飛び越えることができる (\(N\) は大きな整数であり、値は後で指定する)。白のキングは金庫の "右耳" から入り、内部にある駒を全て飛び越し、"左耳"から出ていくことができる。両方の耳には駒が通ることのできる通路があり、この通路の壁も駒二つ分の厚さがある。通路には白いキングが侵入するための隙間がいくつか空いており、"耳" の長さは他のガジェットの数によって決まる。
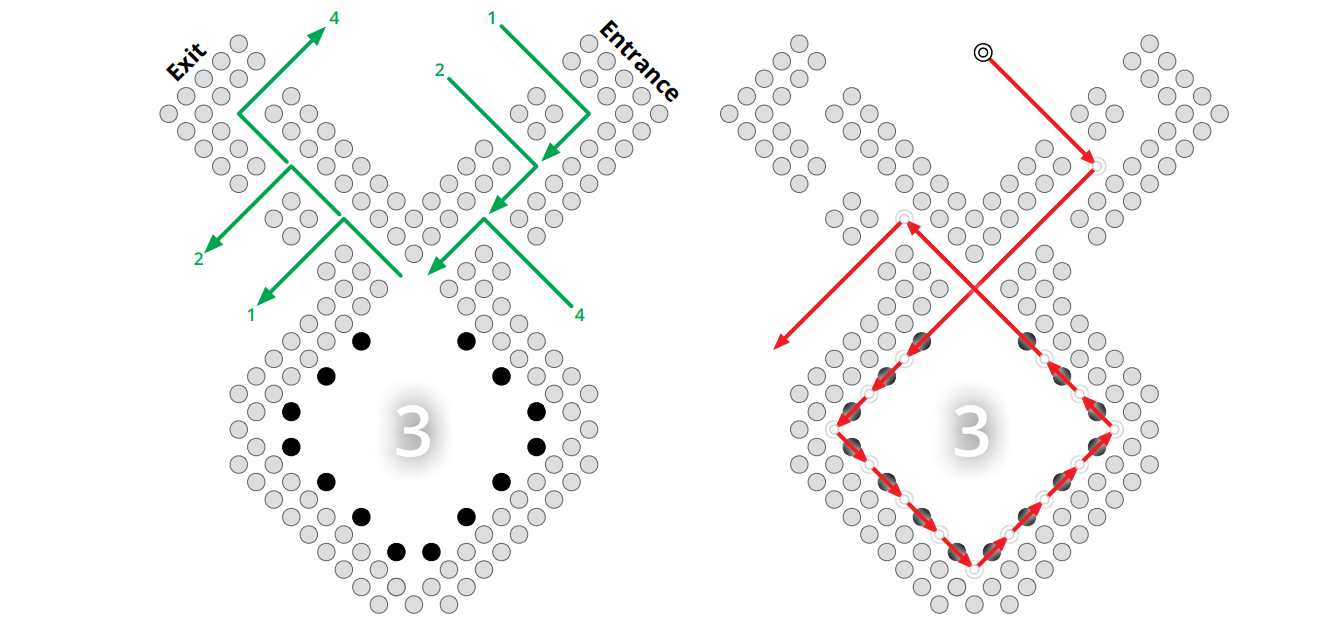 図 12.20左: 三つの入口と三つの出口を持つ頂点ガジェット。右: 金庫を空にする白いキング。灰色の円は飛び越すことができない黒い駒を表す。
図 12.20左: 三つの入口と三つの出口を持つ頂点ガジェット。右: 金庫を空にする白いキング。灰色の円は飛び越すことができない黒い駒を表す。 -
任意の弧 \(i \rightarrow j\) について、白いキングが \(i\) から \(j\) へと方向転換するための曲がり角ガジェットが置かれる。
-
二つの弧が交わる場所には交差点ガジェットが置かれる。このガジェットは白いキングが弧をたどるのを妨げないが、交差するもう一方の弧に進むことを許さない。
 図 12.21左: 曲がり角ガジェットに対する二つある路のうち一つ。右: 交差点ガジェットに対する二つある路のうち一つ。
図 12.21左: 曲がり角ガジェットに対する二つある路のうち一つ。右: 交差点ガジェットに対する二つある路のうち一つ。
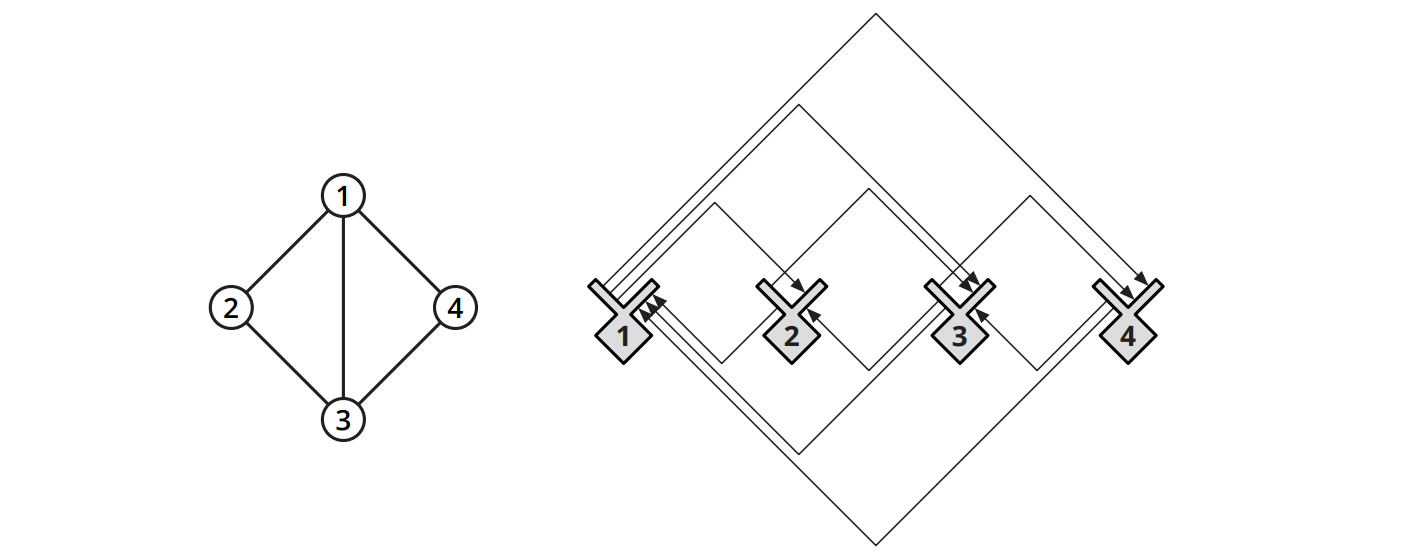
初期盤面では一つの白いキングはいずれかの金庫の下部に置かれ、弧をたどって金庫を空にしていく動きを行えます。\(G\) のハミルトン閉路の逆も \(G\) のハミルトン閉路なので、ガジェットの入口と出口を反転させても構いません。
\(G\) がハミルトン閉路を持つ場合、白いキングは全ての金庫を訪れて最低でも \(nN\) 個の駒を飛び越したうえでスタート地点に戻ってくることができます。一方 \(G\) がハミルトン閉路を持たない場合には、白いキングは少なくともスタート地点の金庫にある黒い駒の半分を飛び越えることができないので、全体で飛び越えることになる黒い駒の数は最大でも \((n - 1 / 2)N + O(n^{3})\) 個となります。ここで \(O(n^{3})\) は曲がり角ガジェットと交差点ガジェットの分です (任意の弧には一つの曲がり角ガジェットと最大 \(n^{2} / 2\) 個の交差点ガジェットが含まれます)。
以上より \(N=n^{4}\) とすれば帰着が完成します。全体としては \(O(n^{5}) \times O(n^{5})\) の盤面となり、\(O(n^{5})\) 個の黒い駒と一つの白いキングを含みます。この構築は総当たりを使っても多項式時間で行えます。完全な盤面の例を次に示します。なお次の問題が NP 困難であるかどうかは未解決です: 「\(n \times n\) の国際ドラフツの盤面が与えられる。白は黒い駒を全て飛び越すことができる (そしてルール上必ずそうすることになる) か?」
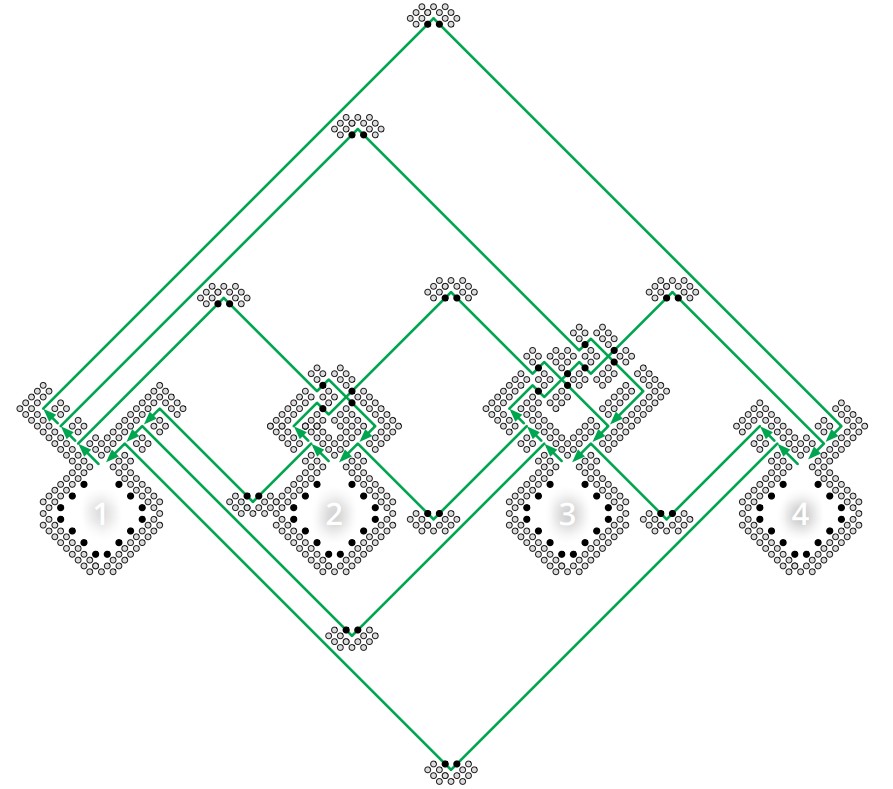
-
Theoretical Computer Science Stack Exchange より: http://cstheory.stackexchange.com/a/1999/111[return]