勝てないゲーム

赤いスーツに身を包んだ、Tom Waits よろしくいかつい顔をしたセールスマンが、\(n\) 個のスイッチと一つの電球の付いた黒い金属の箱をあなたに見せてきました。セールスマンによると、箱の中にはブール回路 ――たくさんの \(\textsc{And}\), \(\textsc{Or}\), \(\textsc{Not}\) を繋いだもの―― が入っており、その回路の入力が \(n\) 個のスイッチで、出力が電球であるとのことです。

そして彼は次の質問をしました: 「電球を灯らせる入力は存在するか？」もし質問に正しく答えることができたら、あなたはその箱と 一億 一兆ドルを入手でき、答えが間違っていた場合および答えを出すことなくあなたが死亡した場合には、彼があなたの魂を奪うと言います。

見たところ、敵はまだどのスイッチも電球に繋いでいないようです。そのためどうスイッチを動かしたとしても電球が灯ることはありません。もしあなたが「明かりを灯すことができる」と答えた場合、敵は箱を開けて回路が何も無いことを見せるでしょう。しかしもしあなたが \(2^{n}\) 個のスイッチの設定を全て試す前に「明かりを灯すことはできない」と答えた場合、敵は魔法の力であなたがまだ試していない設定に限って明かりがつくような回路を作成し、スイッチをその設定にして明かりを灯して見せるでしょう (答えが敵によって確認されるまでは箱の中を見ることはできないので、敵がインチキをしているのを見破ることはできません)。

敵の質問に証明付きで正しく答えるには、実際に \(2^{n}\) 個の設定を全てを試すしかありません。しかしこうすると問題を解くのにあなたの人生よりもはるかに長い時間が必要になることは明らかなので、あなたは敵のオファーを礼儀正しく断ることになります。

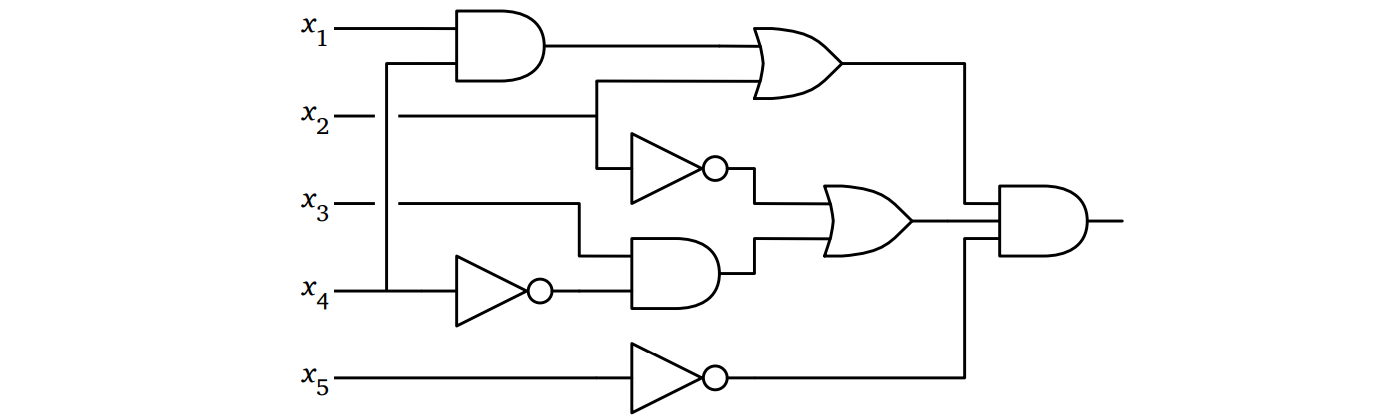
敵は一カートンのマルボロを吸ってから、微笑んで、Heath Ledger 演じるジョーカーのようなどすの利いた声で言います「えぇ、もちろん、あなたは私のことなんて信じない。でも、こうすれば安心でしょう」 彼は特大の羊皮紙 ――本当に羊の皮からできているといいのですが―― をあなたに手渡しました。そこには回路図が書かれています。おそらく彫られているのでしょう。「それは箱の中にある回路の回路図だ。箱の中を見てその図の通りに回路が組まれているか調べてもらって構わない。あるいは回路図から実際の回路を作ってもいいし、コンピューターを使ってシミュレーションをしてもいい。何をしてもいい。もしその回路図が箱の中にある実際の回路と違っていると示せたら、そのときも一兆ドルを渡そう」いくつかの設定を調べてみたところ、どうやら回路図に間違いはないようです。また小細工も不可能に見えます。

しかしこの "気前の良い" オファーもまた断るべきです。敵が示した問題は回路充足問題 (circuit satisfiability problem) または \(\textsc{CircuitSAT}\) と呼ばれます。つまり、与えられられたブール回路の入力で回路の出力が \(\textsc{True}\) になるものが存在するかを判定する問題です。全ての入力に対して \(\textsc{False}\) を返すかどうかを判定する問題とも言えます。

特定の入力に対する出力の計算は深さ優先を使うことで多項式時間で (実は線形時間で) 行えます。しかし \(\textsc{CircuitSAT}\) に対する \(2^{n}\) 個の入力全てを考える場合には、指数時間を使って総当たりで試すよりも速く解く方法を知っている人は誰もいません。確かに、総当たりよりも高速にはできないときちんと証明した人は誰もいません ――なのでもしかしたら、万が一には、まだ発見されていない賢いアルゴリズムがあるのかもしれません―― が、反重力ユニコーンが存在しないときちんと証明した人もいないのです。現実世界で私たちが解くことになるデータに対しては、\(\textsc{CircuitSAT}\) に対する高速なアルゴリズムは存在しないと思った方が安全でしょう。

セールスマンに No を伝えると、彼は微笑んでから「見た目よりは賢いようだな、小僧」と言って、反重力ユニコーンに乗って飛び去って行きましたとさ。