練習問題

1. $\textsc{Partition}$ を $O(nM)$ 時間で解くアルゴリズムを説明、解析してください。ここで $n$ は入力の集合の大きさ、$M$ は入力の集合の要素の和を表します。
2. このアルゴリズムが P=NP を意味しないのはなぜですか？
$\textsc{BoxDepth}$ と呼ばれる次の問題を考えます:「辺が $x, y$ 軸に平行な $n$ 個の長方形の集合が与えられる。共通する点が存在するようなこの集合の部分集合で最大のものの大きさはいくつか？」
1. $\textsc{BoxDepth}$ から $\textsc{MaxClique}$ への多項式時間帰着を説明してください。
2. $\textsc{BoxDepth}$ に対する多項式時間アルゴリズムを説明、解析してください。 [ヒント: 簡単に得られるのは $O(n^{3})$ 時間のアルゴリズムですが、$O(n\log n)$ 時間のアルゴリズムもあります。]
3. この二つの結果から P=NP と結論できないのはなぜですか？
論理式が選言標準形 (disjunctive normal form, DNF) であるとは、式がいくつかの項 (term) の選言 ($\textsc{Or}$) であり、それぞれの項が一つ以上のリテラルの連言 ($\textsc{And}$) であることを言います。例えば \[ (\overline{x} ∧ y ∧ \overline{z}) ∨ (y ∧ z) ∨ (x ∧ \overline{y} ∧ \overline{z}) \] は選言標準形の論理式です。$\textsc{DNF-SAT}$ とは選言標準形の式が入力として与えられたときに、その式が充足可能かを判定する問題です。
1. $\textsc{DNF-SAT}$ に対する多項式時間アルゴリズムを説明してください。
2. 次に示す P=NP の "証明" はどこが間違っていますか？
  
  全ての節に最大でも三つしかリテラルを含まない連言標準形の式が与えられ、その式が充足可能かどうかを知りたいとする。
  
  分配法則を使えば与えられた式を選言標準形に変換できる。例えば \[ \begin{aligned} & (x ∨ \overline{y} ∨ \overline{z}) ∧ (\overline{x} ∨ \overline{y}) \\ & \iff (x ∧ \overline{y}) ∨ (y ∧ \overline{x}) ∨ (\overline{z} ∧ \overline{x}) ∨ (\overline{z} ∧ \overline{y}) \end{aligned} \] となる。(a) のアルゴリズムを使えばこの DNF 式が充足可能であるかどうかを多項式時間で判定できるので、NP 困難である $\textsc{3Sat}$ を多項式時間で解くことができる。よって P=NP でなければならない！
$\textsc{AllOrNothing3SAT}$ は与えられた 3CNF 論理式について、変数への真偽値割り当てであって任意の節が三つの $\textsc{True}$ リテラルを持つか、そうでなければ三つの $\textsc{False}$ リテラルを持つようなものが存在するかを判定する問題です。
1. $\textsc{AllOrNothing3SAT}$ を解く多項式時間アルゴリズムを説明してください。
2. しかし $\textsc{3SAT}$ は NP 困難です！ (a) のアルゴリズムが P=NP を意味しないのはどうしてですか？
1. 任意の重み付きグラフの最短ハミルトン閉路の長さを多項式時間で計算する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、任意の重み付きグラフのハミルトン閉路を計算する多項式時間アルゴリズムを説明、解析してください。
2. 任意のグラフ $G$ を入力として受け取って $G$ に含まれる最大の完全部分グラフの大きさを多項式時間で出力する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、任意のグラフの最大の完全部分グラフを計算する多項式時間アルゴリズムを説明、解析してください。
3. 任意のグラフが 3-彩色可能かどうかを多項式時間で判定する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、与えられた任意のグラフの 3-彩色を計算するか、そのグラフの 3-彩色は不可能であると正しく報告する多項式時間アルゴリズムを説明、解析してください。 [ヒント: ブラックボックスへの入力はグラフだけです。頂点と辺からなるグラフだけであり、他には何も入力しません。]
4. 任意の論理式が充足可能かどうかを多項式時間で判定する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、与えられた任意の論理式を充足させる真偽値割り当てを計算するか、その式は充足不可能であると正しく報告する多項式時間アルゴリズムを説明、解析してください。
5. 任意の整数の集合 $X$ を入力として受け取って、$X$ を $A, B$ に分割して $\sum A = \sum B$ とできるかどうかを多項式時間で出力する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、与えられた任意の整数の集合を和の等しい二つの部分集合に分割するか、そのような分割は不可能であると正しく報告する多項式時間アルゴリズムを説明、解析してください。
6. ♣ ❤ 任意の拡張正規表現 (定義は本文を参照) $R$ を入力として受け取って、$R$ とマッチする文字列が一つでもあるかどうかを多項式時間で出力する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、与えられた任意の拡張正規表現とマッチする文字列を一つ計算するか、そのような文字列は存在しないと正しく報告する多項式時間アルゴリズムを説明、解析してください。
1. $\textsc{Partition}$ から $\textsc{SubsetSum}$ への多項式時間帰着を説明してください。
2. $\textsc{SubsetSum}$ から $\textsc{Partition}$ への多項式時間帰着を説明してください。
ハミルトン閉路問題には無向グラフに関するものと有向グラフに関するものという二つのバージョンがあります。この章では無向ハミルトン閉路問題が NP 困難であることの証明を二つ示しました。
1. 無向ハミルトン閉路問題から有向ハミルトン閉路問題への多項式時間帰着を説明してください。帰着が正しいことを証明してください。
2. 有向ハミルトン閉路問題から無向ハミルトン閉路問題への多項式時間帰着を説明してください。帰着が正しいことを証明してください。
3. 無向ハミルトン閉路問題の NP 困難性を示しているのは二つの帰着のうちどちらですか？
1. $\textsc{HamiltonianPath}$ から $\textsc{HamiltonianCycle}$ への多項式時間帰着を説明してください。
2. $\textsc{HamiltonianCycle}$ から $\textsc{HamiltonianPath}$ への多項式時間帰着を説明してください。[ヒント: 多項式時間帰着はブラックボックスのサブルーチンを複数回呼んでも構いませんが、必ずそうしなければならないというわけではありません。]
$\textsc{PlanarCircuitSAT}$ が NP 困難であることを証明してください。 [ヒント: 交差する配線に対するガジェットを構築してください。]
$\textsc{NotAllEqual3SAT}$ が NP 困難であることを証明してください。
$\textsc{1-In-3SAT}$ が NP 困難であることを証明してください。
この問題では $\textsc{CNFSAT}$ を少しだけ変更した問題を考えます。それぞれの問題において入力は連言標準形の論理式 $\Phi$ であり、目標は $\Phi$ を充足させる真偽値割り当てが存在するかを判定することです。
1. $\Phi$ の各節が最大でも三つのリテラルを含み、各変数は最大でも三つの節にしか現れないとします。このように変更した $\textsc{CNFSAT}$ が NP 困難であることを示してください。
2. $\Phi$ の各節がちょうど三つのリテラルを含み、各変数は最大でも四つの節にしか現れないとします。このように変更した $\textsc{3SAT}$ が NP 困難であることを示してください。 [ヒント: (a) を先に解いてください。]
3. ❤ $\Phi$ の各節が任意の数のリテラルを含み、各変数は最大でも二つの節にしか現れないとします。このように変更した $\textsc{CNFSAT}$ に対する多項式時間アルゴリズムを説明してください。
4. ❤ $\Phi$ の各節がちょうど三つのリテラルを含み、各変数は最大でも三つの節にしか現れないとします。このとき $\Phi$ が充足可能なことを示してください (このように変更した $\textsc{3SAT}$ は完全に自明な問題となります！)。
論理式が排他論理和連言標準形 (exclusive-or conjunctive normal form, XCNF) であるとは、式がいくつかの節の連言 ($\textsc{And}$) からなっていて、それぞれの節がリテラルの排他的論理和であることを言います。つまり、節が真となるのは真のリテラルが奇数個含まれるときだけです。$\textsc{XCNF-SAT}$ 問題とは XCNF 式が充足可能かを判定する問題です。

$\textsc{XCNF-SAT}$ に対する多項式時間アルゴリズムを説明するか、$\textsc{XCNF-SAT}$ が NP 困難であることを証明してください。 [ヒント: 両方は無理です。]
❤ $\textsc{3SAT}$ を少し変更した $\textsc{Majority3SAT}$ を考えます。$\textsc{Majority3SAT}$ の入力は $\textsc{3SAT}$ と同じく各節がちょうど三つのリテラルを持つ連言標準形の論理式 $\Phi$ であり、出力は $\Phi$ の変数への真偽値割り当てであって全ての節が少なくとも二つの $\textsc{True}$ を持つものが存在するかどうかです。

$\textsc{Majority3SAT}$ を多項式時間で解くアルゴリズムを説明するか、$\textsc{Majority}$$\textsc{3SAT}$ が NP 困難であると証明してください。 [ヒント: 両方は無理です。]
♠ ❤ 任意の部分集合 $X \subset \lbrace 0, 1, 2, 3 \rbrace $ について、次の問題 (ここでは $\textsc{X-3SAT}$ と呼びます) を考えます。入力は各節がちょうど三つのリテラルを持つ連言標準形の論理式 $\Phi$ であり、出力は $\Phi$ の変数への真偽値割り当てであって $\Phi$ に含まれる $\textsc{True}$ リテラルの数が $X$ に含まれるものです。例えば:
- $\lbrace 1, 2, 3 \rbrace \textsc{-3SAT}$ は普通の $\textsc{3SAT}$ です。
- $\lbrace 0, 3 \rbrace \textsc{-3SAT}$ は $\textsc{AllOrNothing3SAT}$ です (練習問題 12.4)。
- $\lbrace 1, 2 \rbrace \textsc{-3SAT}$ は $\textsc{NotAllEqual3SAT}$ です (練習問題 12.10)。
- $\lbrace 1 \rbrace \textsc{-3SAT}$ は $\textsc{1-IN-3SAT}$ です (練習問題 12.11)。
- $\lbrace 2, 3 \rbrace \textsc{-3SAT}$ は $\textsc{Majority3SAT}$ です (練習問題 12.14)。
$\textsc{X-SAT}$ が多項式時間で解けるような部分集合 $X \subset \lbrace 0,1,2,3 \rbrace$ の完全なリストを作ってください。P $\neq$ NP を仮定してください。 [ヒント: 16 個の異なる問題を解くのはやめてください。]
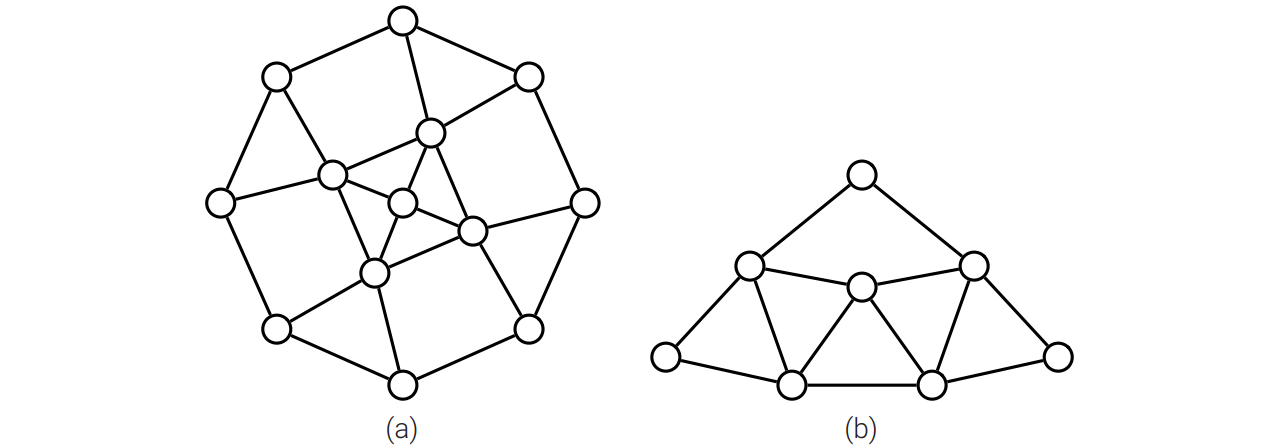
1. 下図 (a) のガジェットを使って、平面グラフが 3-彩色可能であるかを判定する問題が NP 困難であることを示してください。 [ヒント: ガジェットが 3-彩色可能であることを示し、任意のグラフの平面への埋め込みにおける交差をこのガジェットで適切に置き換えてください。]
2. (a) と下図 (b) のガジェットを使って、最大次数が 4 の平面グラフが 3-彩色可能であるかを判定する問題が NP 困難であることを示してください。 [ヒント: 次数が 4 よりも大きい全ての頂点を複数のガジェットを使って置き換え、全ての頂点の次数を 4 以下にしてください。]
次の問題が NP 困難であることを示してください。
1. 無向グラフ $G$ が与えられる。$G$ には 17 個の頂点を除いた全ての頂点を訪れる単純路があるか？
2. 無向グラフ $G$ が与えられる。$G$ には全ての頂点の次数が 23 以下の全域木があるか？
3. 無向グラフ $G$ が与えられる。$G$ には葉の数が 42 以下の全域木があるか？
4. 無向グラフ $G = (V, E)$ が与えられる。部分集合 $S \subseteq V$ であって両端が $S$ に含まれる $E$ の辺の数が 374 本以下であるものの大きさの最大値はいくつか？
5. 無向グラフ $G = (V, E)$ が与えられる。部分集合 $S \subseteq V$ であって $S$ に含まれる任意の頂点に隣接する頂点の数が 473 個以下であるものの大きさの最大値はいくつか？
6. 無向グラフ $G$ が与えられる。最大でも 31337 本の辺だけが両端に同じ色を持つように $G$ の頂点を三色で彩色できるか？
最小全域木問題を改変した次の問題が NP 困難であることを示してください。
1. 無向グラフ $G$ が与えられたときに、$G$ の全域木で半径が最大のものを求める (全域木 $T$ の半径とは $T$ に含まれる路の長さの最大値を言う)。
2. 辺に重みの付いた無向グラフ $G$ が与えられたときに、$G$ の深さ優先探索木の中で重みが最小のものを求める。
3. 辺に重みの付いた無向グラフ $G$ と $G$ の頂点の部分集合 $S$ が与えられたときに、全ての葉が $S$ に含まれるような全域木の中で重みが最小のものを計算する。
4. 辺に重みの付いた無向グラフ $G$ と整数 $l$ が与えられたときに、葉が $l$ 個以下の全域木の中で重みが最小のものを計算する。
5. 辺に重みの付いた無向グラフ $G$ と整数 $\Delta$ が与えられたときに、全ての頂点の次数が $\Delta$ 以下の全域木の中で重みが最小なものを計算する。
3 という数字には特別な意味があります。
1. $\textsc{2Partition}$ に対する多項式時間アルゴリズムを説明、解析してください。アルゴリズムの入力は $2n$ 個の正の整数の集合 $S$ であり、出力は $S$ を $n$ 個の互いに重ならない整数の組に分割し、その上で $n$ 個の組の和が全て等しいようにできるかどうかです。
2. $\textsc{2Color}$ に対する多項式時間アルゴリズムを説明、解析してください。アルゴリズムの入力は無向グラフ $G$ であり、出力は二つの色だけを使って $G$ を彩色できるかどうかです。
3. $\textsc{2SAT}$ に対する多項式時間アルゴリズムを説明、解析してください。アルゴリズムの入力は各節が二つのリテラルからなる連言標準形の論理式 $\Phi$ であり、出力は $\Phi$ が充足可能かどうかです。 [ヒント: この問題は以前の章で説明したことと強い関連があります。]
3 という数字に特別な意味なんてありません。
1. $\textsc{12Partition}$ 問題は次のように定義されます: 「$12n$ 個の正の整数の集合 $S$ が与えられたとき、 $S$ を大きさが 12 の集合 $n$ 個に分割し、さらに $n$ 個の集合の和が全て等しいようにできるかを判定する」 $\textsc{12Partition}$ が NP 困難であることを示してください。 [ヒント: $\textsc{3Partition}$ からの帰着です。最初は多重集合を考えた方が簡単かもしれません。]
2. $\textsc{12Color}$ 問題は次のように定義されます: 「無向グラフ $G$ が与えられたときに、どの辺の端点も同じ色にならないように各頂点を 12 色のうちどれかで塗っていくことができるかを判定する」 $\textsc{12Color}$ が NP 困難であることを示してください。 [ヒント: $\textsc{3Color}$ からの帰着です。]
3. $\textsc{12SAT}$ は次のように定義されます: 「各節にちょうど 12 個のリテラルが含まれるような連言標準形の論理式 $\Phi$ が与えられたときに、$\Phi$ が充足可能かどうかを判定する」 $\textsc{12SAT}$ が NP 困難であることを示してください。 [ヒント: $\textsc{3SAT}$ からの帰着です。]
1. $\textsc{3SAT}$ から $\textsc{4SAT}$ への多項式時間帰着を説明してください。
2. $\textsc{4SAT}$ から $\textsc{3SAT}$ への多項式時間帰着を説明してください。
❤ $\textsc{4Color}$ から $\textsc{3Color}$ への直接的な多項式時間帰着を説明してください (これは逆方向の帰着よりもはるかに難しいです)。
整数の書かれた正方形を二つつなげたものをドミノと言います¹。横一列に並んだドミノの並べ方が合法であるとは、隣り合う正方形に書かれた数字が同じことを言います。

次の問題に対する多項式時間アルゴリズムを説明するか、問題が NP 困難であることを示してください。
1. $D$ 個のドミノの集合が与えられる。$D$ に含まれる全てのドミノを合法に並べることはできるか？
2. $D$ 個のドミノの集合が与えられる。$D$ に含まれるドミノの合法な並べ方で $1$ から $n$ までの数字がちょうど二回ずつ現れるものは存在するか？
  
  $$0$ から $6$ までの数字が二回ずつ現れる合法な並べ方$
  
  図 12.24
  
  $0$ から $6$ までの数字が二回ずつ現れる合法な並べ方
3. ❤ $D$ 個のドミノの集合が与えられる。$D$ に含まれるドミノを合法に並べるとき、最大でいくつのドミノを使うことができるか？
ぺブリング (pebbling) は無向グラフ $G$ を使って遊ぶ一人用ゲームです。$G$ の各頂点にゼロ個以上の小石 (pebble) を置いた状態からゲームが始まります。プレイヤーが各手で行える唯一の操作は、適当な頂点 $v$ を選んで $v$ の小石を二つ取り除き、$v$ に隣接する適当な頂点に小石を一つ追加するという操作です (もちろん二つ以上の小石の置かれた $v$ しか選ぶことができません)。

$\textsc{PebbleDestruction}$ 問題の入力は無向グラフ $G = (V,E)$ と各頂点 $v$ に対する小石の数 $p(v)$ であり、出力は小石を最後の一つになるまで取り除く手の列です。$\textsc{PebbleDestruction}$ が NP 困難であることを示してください。
無向グラフ $G$ の 5-彩色とは、$G$ の頂点に $\lbrace 0,1,2,3,4 \rbrace$ のどれかの "色" を塗って、任意の辺 $uv$ に対して $u$ と $v$ に違う色が割り当てられるようにする関数であることを思い出してください。5-彩色が慎重 (careful) であるとは、任意の頂点に対して隣接する頂点の色が異なっているだけではなく色の値が (mod 5 で) 2 以上離れていることを言います。無向グラフに慎重な 5-彩色が存在するかどうかを判定する問題が NP 困難であることを示してください。 [ヒント: 通常の $\textsc{5Color}$ 問題から帰着させてください。]

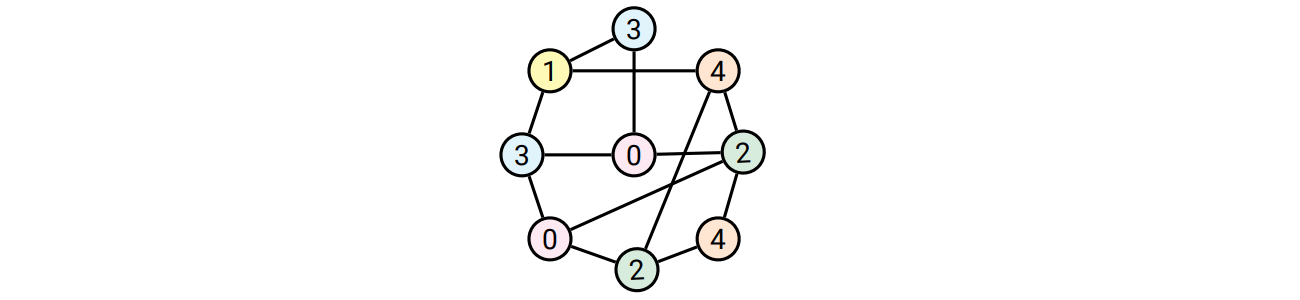図 12.25

慎重な 5-彩色
1. 無向グラフ $G$ の頂点の部分集合 $S$ が半独立 (half-independent) であるとは、$S$ の各頂点が最大でも一つの $S$ の頂点としか隣接していないことを言います。与えられた無向グラフの最大半独立集合を求める問題が NP 困難であることを示してください。
2. 無向グラフ $G$ の頂点の部分集合 $S$ がなんとなく独立 (sort-of-independent) であるとは、$S$ の各頂点が最大でも 374 個の $S$ の頂点としか隣接していないことを言います。与えられた無向グラフの最大なんとなく独立集合を求める問題が NP 困難であることを示してください。
3. 無向グラフ $G$ の頂点の部分集合 $S$ がほぼ独立 (almost independent) であるとは、両端点が $S$ に含まれる $G$ の辺が 374 個以下であることを言います。与えられた無向グラフの最大ほぼ独立集合を求める問題が NP 困難であることを示してください。
無向グラフ $G$ の頂点の部分集合 $S$ が三角形を含まない (triangle-free) とは、任意の三つの頂点 $u,v,w \in S$ について辺 $uv, uw, vw$ のどれかが $G$ に含まれないことを言います。与えられた無向グラフの含まれる三角形を含まない頂点集合の中で最大のものを見つける問題が NP 困難であることを示してください。

図 12.26

三角形を含まない大きさ 7 の頂点集合 (この集合はこのグラフに含まれる三角形を含まない頂点集合の中で最大のものではない)
無向グラフ $G = (V. E)$ の頂点の部分集合が支配集合 (dominating set) であるとは、$G$ の全ての頂点が $S$ に含まれるか、そうでなければ $S$ に隣接することを言います。$\textsc{DominatingSet}$ 問題は無向グラフ $G$ と整数 $k$ を入力として受け取って $G$ に大きさ $k$ の支配集合が存在するかどうかを判定する問題です。この問題が NP 困難であることを示してください。

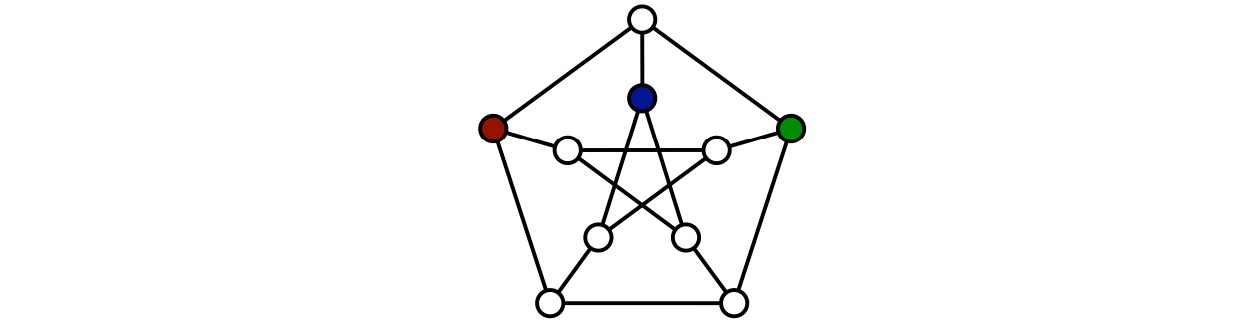図 12.27

Petersen (ピーターセン) グラフにおける大きさ 3 の支配集合
$\textsc{RectangleTiling}$ 問題は次のように定義されます: 「大きな長方形といくつかの小さな長方形が与えられたときに、大きな長方形の中に小さな長方形を隙間も重なりもなく敷き詰めることができるかを判定する」
1. $\textsc{RectangleTiling}$ が NP 困難であることを示してください。
2. $\textsc{RectangleTiling}$ が強 NP 困難であることを示してください。
$$\textsc{RectangleTiling}$ 問題の答が $\textsc{True}$ となるインスタンス$

図 12.28

$\textsc{RectangleTiling}$ 問題の答が $\textsc{True}$ となるインスタンス
辺に重みの付いた無向グラフを $G$ とします。$G$ の重い (heavy) ハミルトン閉路とは、$G$ の全ての頂点をちょうど一回ずつ通り抜ける閉路 $C$ であって $C$ の重みが $G$ に含まれる辺の重みの和の半分より大きいものを言います。与えられたグラフが重いハミルトン閉路を持つかどうかを判定する問題が NP 困難であることを示してください。

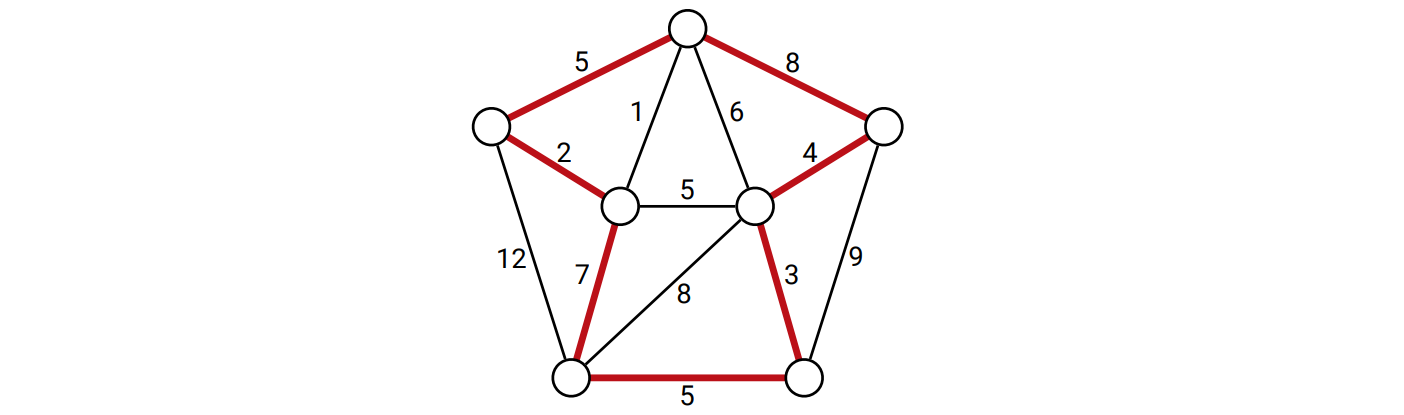図 12.29

重いハミルトン閉路 (閉路の重みは 37 であり、グラフ全体の重みは 67 である)
1. 無向グラフ $G$ のトニアン路 (tonian path) とは、 $G$ の半分以上の頂点を訪れる路のことを言います。グラフがトニアン路を含むかどうかを判定する問題が NP 困難であることを示してください。
2. 無向グラフ $G$ のトニアン閉路 (tonian cycle) とは、 $G$ の半分以上の頂点を訪れる閉路のことを言います。グラフがトニアン閉路を含むかどうかを判定する問題が NP 困難であることを示してください。 [ヒント: (a) を使うか、あるいは使わないでください。]
1. 無向グラフ $G$ の頂点の部分集合 $B$ が Burr (バー) 集合であるとは、$G$ から $B$ に含まれる頂点を全て取り除いて得られる部分グラフがハミルトン閉路を含まないことを言います。与えられた無向グラフの最小 Burr 集合を見つける問題が NP 困難であることを示してください。
2. 無向グラフ $G$ の頂点の部分集合 $S$ が Schuyler (スカイラー) 集合であるとは、$G$ から $S$ に含まれる頂点を全て取り除いて得られる部分グラフがハミルトン閉路を含むことを言います。与えられた無向グラフの最大 Schuyler 集合を見つける問題が NP 困難であることを示してください。
この問題では $\textsc{VertexCover}$ から $\textsc{SteinerTree}$ へのとある帰着が正しいことを示します。無向グラフ $G = (V, E)$ の最小頂点被覆を見つけたいとして、$H = (V^{\prime}, E^{\prime})$ を次のように構築します:
- $V^{\prime} = V \cup E \cup \lbrace z \rbrace$
- $E^{\prime} =$ $\lbrace ve\ |\ v \in V \text{ は } e \in E \text{ の端点} \rbrace$ $\cup $ $\lbrace vz\ |\ v \in V \rbrace$
この定義を言い換えると、$G$ の各辺を頂点で置き換え、さらに新しく "先端の" 頂点 $z$ を加えて、全ての頂点を $z$ と結んだものが $H$ だということです。

$G$ に大きさ $k$ の頂点被覆が存在するときに限って $H$ には $E \cup \lbrace z \rbrace$ を含む大きさ $k\ +$ $|E|\ +$ $1$ の部分木が存在することを示してください。
次に示す問題に対する多項式時間アルゴリズムを説明するか、問題が NP 困難であることを示してください。
1. 無向グラフ $G$ の各辺をちょうど二回ずつ使う閉じた歩道を二重オイラー周遊 (double-Eulerian tour) と呼ぶ。無向グラフ $G$ が与えらたとき、$G$ は二重オイラー周遊を持つか？
2. 無向グラフ $G$ の各頂点をちょうど二回ずつ訪れる閉じた歩道を二重ハミルトン周遊 (double-Hamiltonian tour) と呼ぶ。無向グラフ $G$ が与えられたとき、$G$ は二重ハミルトン周遊を持つか？
3. 無向グラフ $G$ の各頂点をちょうど二回ずつ、各辺を最大でも一回ずつ訪れる閉じた歩道を二重ハミルトン回路 (double-Hamiltonian circuit) と呼ぶ。無向グラフ $G$ が与えられたとき、$G$ は二重ハミルトン回路を持つか？
4. 無向グラフ $G$ の各辺をちょうど三回ずつ使う閉じた歩道を三重オイラー周遊 (triple-Eulerian tour) と呼ぶ。無向グラフ $G$ が与えらたとき、$G$ は三重オイラー周遊を持つか？
5. 無向グラフ $G$ の各頂点をちょうど三回ずつ訪れる閉じた歩道を三重ハミルトン周遊 (triple-Hamiltonian tour) と呼ぶ。無向グラフ $G$ が与えられたとき、$G$ は三重ハミルトン周遊を持つか？
次の一人用ゲームを考えます。$n \times m$ の格子のいくつかのマスに赤と青の石が置かれた状態からゲームが始まり、ゲームの目標は石をいくつか取り除いて次の条件が成り立つようにすることです:
1. どの行にも少なくとも一つの石が含まれる。
2. 各列には同じ色の石しか含まれない。
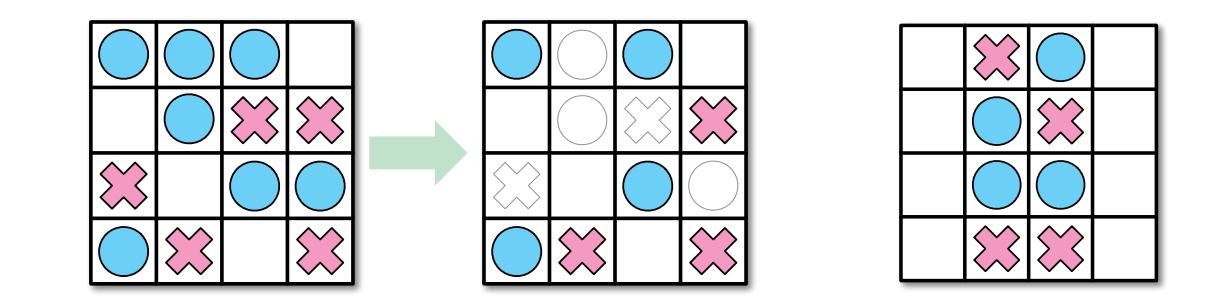図 12.30

左のパズルにはたくさんの解法があるが、右のパズルはどうやっても解けない

青い石と赤い石の初期配置が与えられたときに、それが解けるかどうかを判定する問題が NP 困難であることを示してください。
$n \times m$ の格子とそのマスに置くことができる石を使ったゲームを考えます。初期配置としてマスのいくつかに石が置かれた格子が与えられ、プレイヤーが行える操作はいずれかの列にある石を全て取り除くという操作だけです。
1. 各行にある石の数を一つ以下にするときに、取り除くことになる列の部分集合の中で最小のものを見つける問題が NP 困難であることを示してください。
2. 各行にある石の数を一つ以上に保ったまま取り除くことができる列の部分集合の中で最大のものを見つける問題が NP 困難であることを示してください。
3. ❤ いくつかの列を取り除くことで、全ての行にある石の数をちょうど一つにできるかどうかを判定する問題が NP 困難であることを示してください。
Jeff は生徒が満足できるような講義をしたいと思っているので、講義の最初にどんな方針で講義を行ってほしいかを尋ねるアンケートを取っています。アンケートには講義の方針が一覧で示され、生徒はそれぞれに「こうしてほしい」、「どちらでもない」、「こうしないでほしい」のいずれかを答えます。ただし「こうしてほしい」と「こうしないでほしい」を答えられるのは合わせて 5 回までです。Jeff の生徒はとても寛容なので、生徒が満足するのは「こうしてほしい」方針がちょうど一つ採用されたときか、そうでなければ「こうしないでほしい」方針がちょうど一つ採用されなかったときです (満足するのはこのどちらかのときだけです)。

満足する生徒の数を最大化する講義の方針を計算する多項式時間アルゴリズムを説明するか、この問題が NP 困難であると示してください。
あなたは地元のコミュニティシアターで開催されるミュージカルの振付師であり、劇の最後で見せる拍手喝采間違いなしのポーズを決めることになりました ("Streetcar!")。そこであなたは曲の終わりで $n$ 人のキャストが一列に並び、手を広げて気迫に満ちた指の動き ("spirit finger") を観客に見せ付けることにしました。

しかしワンマンの監督が最後のシーンで全員が腕を真上か真下に伸ばすことを独断で決定し、さらに自身の繊細な芸術的感性を乱しかねないキャストの腕の伸ばし方をリストにして示しました。リストにはキャストの名前と腕の方向が載っており、キャストにそのような指示をすることはできません。例えば「Ned, Apu, Smithers が腕を下に出すときは Marge は腕を上に出すことができない」などと書かれています。

監督の芸術的感性を満たすような腕の出し方を見つける問題が NP 困難であることを示してください。
次のパーティでは招待客の一人が三チーム対戦マンブレッティーペグ (Three-Way Mumbletypeg) をやろうと提案するでしょう。これは三つのチームとナイフを使って遊ぶゲームであり、公式ルール (1652 年の聖ローマ三チーム対戦マンブレッティーペグ協議会で決定) は以下の通りです:
1. 全てのチームには一人以上のメンバーが必要である。
2. 同じチームの任意の二人は知り合いでなければならない。
3. 試合を観戦する全ての人はいずれかのチームに所属しなければならない。
パーティの参加者の中にはお互いに知り合いでない人も含まれますが、パーティはもちろん楽しいものになるので、誰もパーティを離れたくはありません。パーティのホストはあなたのアルゴリズムの腕前が生かされたスリリングな話を聞きつけ、あなたに参加者の知り合い関係のリストを渡し、チームを作っておくように頼んできました。彼はその間にナイフを研いでおくとのことです。

パーティの参加者を三チーム対戦マンブレッティーペグのチームに分けることができるかを判定する多項式時間アルゴリズムを説明するか、この問題が NP 困難であることを示してください。
あなたが参加しているパーティはとても楽しく進んでいますが、ここでアルゴリズム行進の時間がやってきました。このダンスはコンビ漫才師いつもここからがピタゴラスイッチという日本の子供向けテレビ番組用に作成したものです。アルゴリズム行進では何人かの人が一列に並び、先頭の人から一テンポずつずれながら特定の動きをしていきます。この行進はダンスにおける輪唱あるいはカノンと言うことができます ("Row Row Row Your Boat" や "Frère Jacques" のような感じです)。

エチケット上、この行進をするときにはすぐ前にいる人と知り合いでなければなりません。もしそうしなかった場合には行進を間違えたときに知らない人同士がひどく恥ずかしい思いをしてしまうからです。パーティの参加者の誰と誰が知り合いかを記した完全なリストが与えられたとします。アルゴリズム行進に参加できる最大人数を求める問題が NP 困難であることを示してください。一般性を失うことなくパーティに忍者が参加しないことを仮定して構いません。
♣ 非決定性有限状態オートマトンと正規表現に関する次の問題が NP 困難であることを示してください。
1. アルファベット $\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace$ 上の NFA $M$ が与えられる。$\Sigma^{\ast}$ に含まれる文字列で $M$ が受理しないものは存在するか？
2. アルファベット $\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace$ 上の非巡回 NFA $M$ が与えられる。$\Sigma^{\ast}$ に含まれる $M$ が受理しない最短の文字列は何か？
3. アルファベット $\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace$ 上の正規表現 $R$ が与えられる。$\Sigma^{\ast}$ に含まれる文字列で $R$ とマッチしないものは存在するか？
4. アルファベット $\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace$ 上のスターを含まない正規表現 $R$ が与えられる。$\Sigma^{\ast}$ に含まれる $R$ とマッチしない文字列で最短のものは何か？
(実は (a) と (c) の問題は PSPACE 完全であり、PSPACE に属するという証明さえ自明ではありません)
♣
1. 次の問題に対する多項式時間アルゴリズムを説明してください: 「アルファベット $\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace$ 上の NFA $M$ が与えられる。$\Sigma^{\ast}$ に含まれる文字列で $M$ が受理するものは存在するか？」
2. 次の問題に対する多項式時間アルゴリズムを説明してください: 「アルファベット $\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace$ 上の正規表現 $R$ が与えられる。$\Sigma^{\ast}$ に含まれる文字列で $R$ とマッチするものは存在するか？」
3. 任意の正規表現の否定もまた正規表現です。この問題で答えた二つのアルゴリズムと前問で示した NP 困難性をもって P=NP を結論できないのはどうしてですか？
Charon は最近死亡した $n$ 人の人間の魂を Acheron 川を通って Hades まで船で送って行こうとしています。特定の乗客同士は不倶戴天の敵なので、Charon が一緒にいるときにしか同時に川の同じ岸にいることができません (その二人が一緒にいる状態で Charon が岸を離れると、二人はお互いの口に入った obols の取り合いを始め、彼らの魂は Acheron の岸を永遠に彷徨うことになってしまいます。つまり、とても悪いことが起こります)。船には Charon を含めて $k$ 人が乗ることができ、船を操縦できるのは Charon だけです²。

Charon が $n$ 人の魂を Acheron まで無事に送ることができるかどうかを判定する問題が NP 完全であることを示してください (無事と言いますが、死んでも構いません。元から死んでいるので)。Charon 問題の入力は整数 $n, k$ と乗客の敵対関係を表す $n$ 頂点のグラフ $G$ であり、出力は $\textsc{True}$ または $\textsc{False}$ です。

答えを古典ラテン語で書くのはやめてください。

整数はサイコロと同じように点の数で表されることが多いです。一般的なドミノでは点の数は 0 から 6 であり、大きくても 9 あるいは 12 まで書かれたものがある程度ですが、この問題では任意の大きさの整数が書かれているとします。またドミノは全ての整数の組が書かれたドミノをちょうど一つずつ含むことが普通ですが、この問題ではこのことを仮定しません。^[return]
この問題はよく知られたオオカミ-ヒツジ-キャベツのパズルの一般化です。このパズルが登場する最古の例は歴史的価値の高い中世の写本 Propositiones ad Acuendos Juvenes (Problems to Sharpen the Young, 若者を磨くための問題集) です。

XVIII. Propositio De Homine et Capra et Lvpo.

Homo quidam debebat ultra fluuium transferre lupum, capram, et fasciculum cauli. Et non potuit aliam nauem inuenire, nisi quae duos tantum ex ipsis ferre ualebat. Praeceptum itaque ei fuerat, ut omnia haec ultra illaesa omnino transferret. Dicat, qui potest, quomodo eis illaesis transire potuit?

Solutio. Simili namque tenore ducerem prius capram et dimitterem foris lupum et caulum. Tum deinde uenirem, lupumque transferrem: lupoque foris misso capram naui receptam ultra reducerem; capramque foris missam caulum transueherem ultra; atque iterum remigassem, capramque assumptam ultra duxissem. Sicque faciendo facta erit remigatio salubris, absque uoragine lacerationis.

古典ラテン語は最近読んでいないのでちょっと、というごく少数の読者のために、翻訳もつけておきます:

XVIII. 男とヒツジとオオカミの問題

男はオオカミとヒツジとキャベツを川の向こう木まで送らなければならない。しかし、船が [一度に] 耐えられるのは [男を含めて] 二つ [の重さ] までである。可能ならば、その方法を答えよ: 全ての荷物を無事に向こう岸まで届けることができるか？

答え [前問と] 同じように、最初にヒツジを向こう岸まで連れて行き、こちら側の岸にオオカミとキャベツを残す。その後オオカミを向こう岸に連れて行き、そのとき向こう岸にいるヒツジをこちら側の岸に連れ帰る。その後ヒツジをこちら側の岸に置き、キャベツを向こう岸に持っていく。それからヒツジを連れて向こう岸に渡れば、全員が向こう岸に行くことができ、流血沙汰も起きない。

Propositiones の作者として最も有力視されているのは 8 世紀の英国人学者 Alcuin of York (ヨークのアルクィン) です。Alcuin がこの本の作者であることの証拠は若干状況証拠めいているのですが、彼がカール大帝とのやり取りの中で "算術に関する娯楽目的の問題" を送ったことは分かっています。現代の学者のほとんどは、たとえ Alcuin が本当に Propositiones を書いていたとしても、彼が全ての問題を考え着いたというわけではなく、さらに古い文献から集めてきたのだろうと考えています。

決して変わらないものもあるようです。^[return]