グラフの彩色 (3SAT からの帰着)
グラフ \(G = (V,E)\) の真の \(\pmb{k}\)-彩色 (proper \(\pmb{k}\)-coloring) とは、各頂点に \(k\) 個ある色のどれかを割り当てる関数 \(C: V \rightarrow \lbrace 1, 2, \ldots, k \rbrace\) であって辺でつながれた任意の頂点に違う色が割り当てられるものを言います ("色" は適当なラベルであり、ここでは整数とします。電磁スペクトル、CMYK ベクトル、Pantone の色番号などは使いません)。グラフ彩色問題とは与えられたグラフを彩色するのに必要となる色の数の最小値を計算する問題です。
グラフ彩色問題が NP 困難であることを示すには、与えられたグラフは真の 3-彩色を持つかを判定する \(\textsc{3Color}\) 問題だけを考えれば十分です。これから \(\textsc{3Color}\) が NP 困難なことを \(\textsc{3SAT}\) からの帰着で示します (なぜ \(\textsc{3SAT}\) かというと、問題に \(3\) が含まれているからです。ふざけているのかと思うのかもしれませんが、私は真面目に言っています)。つまり 3CNF 式 \(\Phi\) が与えられたときに、\(\Phi\) が充足可能なときに限って 3-彩色可能となるグラフ \(G\) を作れば良いことになります:
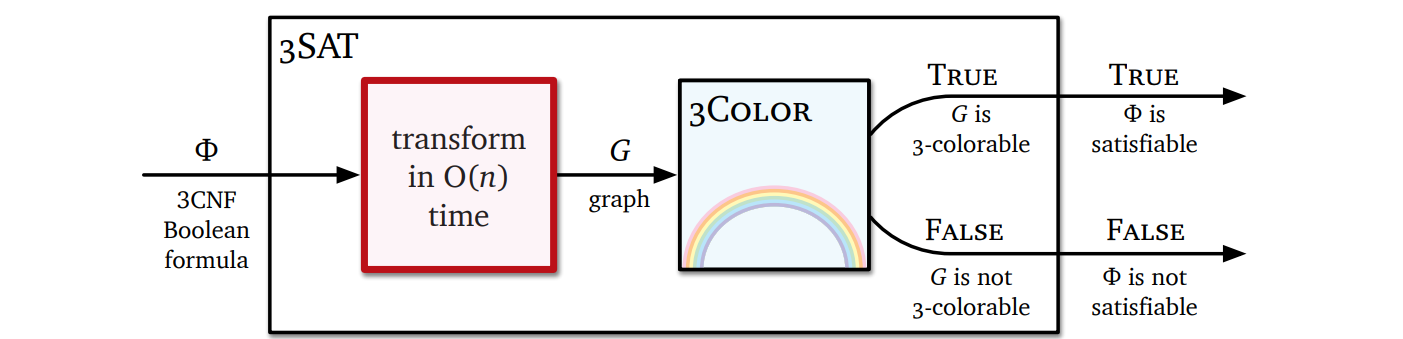
ここでは出力のグラフ \(G\) をガジェット (gadget) ごとに作っていくという、帰着においてよく使われる戦略を使います。\(G\) の各ガジェットが、入力の式 \(\Phi\) が持つ様々な特徴を表します。帰着をガジェットに分解して考えることは既存の帰着を理解するのに有用なだけでなく、NP 困難性を証明するための新しい帰着を考えるときにも有用です1。
今考えている論理式からグラフへの帰着は三つのガジェットからなります:
-
真偽値ガジェット: 三角形をなす頂点 \(T\), \(F\), \(X\) があり、それぞれが \(\textsc{True}\), \(\textsc{False}\), \(\textsc{Other}\) に対応する。この三つの頂点は全て辺でつながっており、3-彩色において異なる色が塗られる。議論を簡単にするために、以降これらの色を \(\textsc{True}\), \(\textsc{False}\), \(\textsc{Other}\) と呼ぶ。例えばある頂点が \(\textsc{True}\) に塗られていると言ったときには、その頂点が \(T\) と同じ色で塗られていることを意味する。
-
変数ガジェット: \(\Phi\) の任意の変数 \(a\) に対して、\(a\) とラベルの付いた頂点、\(\overline{a}\) とラベルの付いた頂点、真偽値ガジェットの頂点 \(X\) からなる三角形がある。\(a\) は \(\textsc{True}\) または \(\textsc{False}\) に塗られ、それに対して \(\overline{a}\) は \(\textsc{False}\) または \(\textsc{True}\) に塗られる。
 図 12.9真偽値ガジェット (左) と変数 \(a\) に対応する変数ガジェット (右)
図 12.9真偽値ガジェット (左) と変数 \(a\) に対応する変数ガジェット (右) -
節ガジェット: \(\Phi\) の各節に対して、三つのリテラルに対応する (変数ガジェットの) 頂点と (真偽値ガジェットの) 頂点 \(T\) を、ラベルの無い頂点を五つ使って次のようにつなぐ:
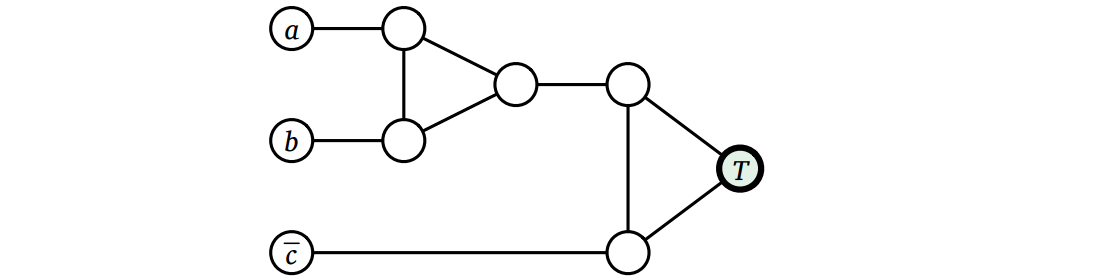 図 12.10\((a \lor b \lor \overline{c})\) に対応する節ガジェット
図 12.10\((a \lor b \lor \overline{c})\) に対応する節ガジェットこうしたとき、二つの三角形は "マジョリティゲート" のように機能する。つまり任意の真の 3-彩色において、もし左の二つの頂点が同じ色だった場合には右の頂点はその色と同じになり、そうでなく左の二つの頂点が違う色であった場合には右の頂点は任意の色になれる (下図参照)。
よって節ガジェットに含まれる三つのリテラルが全て \(\textsc{False}\) になることはないと分かる。逆に節ガジェットに含まれる三つのリテラルに対する二つ以上の色を使った任意の彩色が与えられば、その彩色を節ガジェット全体の彩色に拡張できる。変数ガジェットの構成からリテラルの頂点には \(\textsc{True}\) または \(\textsc{False}\) のどちらかが塗られることが言えるので、節ガジェットの任意の彩色は少なくとも一つのリテラルの頂点に \(\textsc{True}\) を塗る。
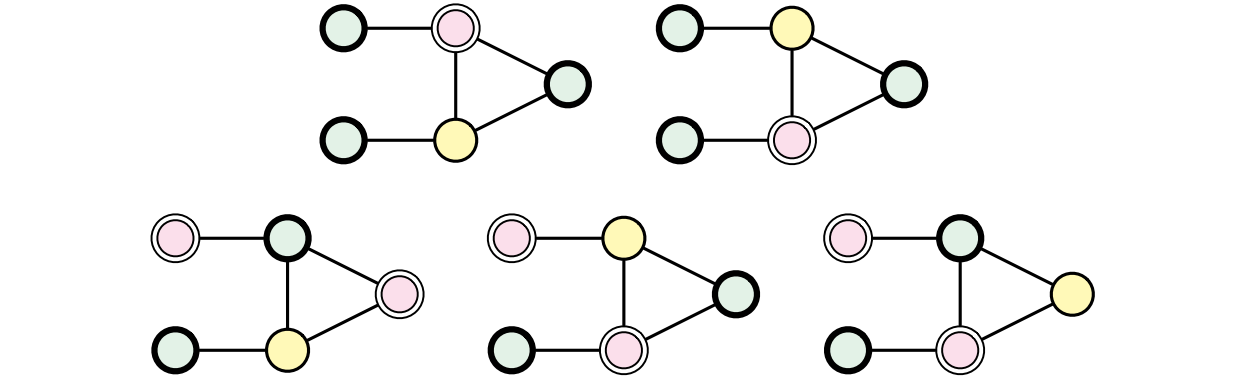 図 12.11「半分の」ガジェットに対する全ての真 3-彩色 (色の置換を同一視している)
図 12.11「半分の」ガジェットに対する全ての真 3-彩色 (色の置換を同一視している)
最終的に出来上がるグラフ \(G\) には、頂点 \(T\), \(F\), \(X\) そして各変数 \(a\) に対応する頂点 \(a\) および \(\overline{a}\) がちょうど一つずつ含まれます。例えば \((a ∨ b ∨ c)\ ∧\) \((b ∨ \overline{c}\ ∨\) \(\overline{d})\ ∧\) \((\overline{a} ∨ c ∨ d)\ ∧\) \((a ∨ \overline{b} ∨ \overline{d})\) という、以前に \(\textsc{MaxClique}\) を説明するときに使った論理式は次のグラフになります。図中の 3-彩色は式を充足させる真偽値割り当ての一つ \(a = b = \textsc{True}\), \(b = d = \textsc{False}\) に対応します。
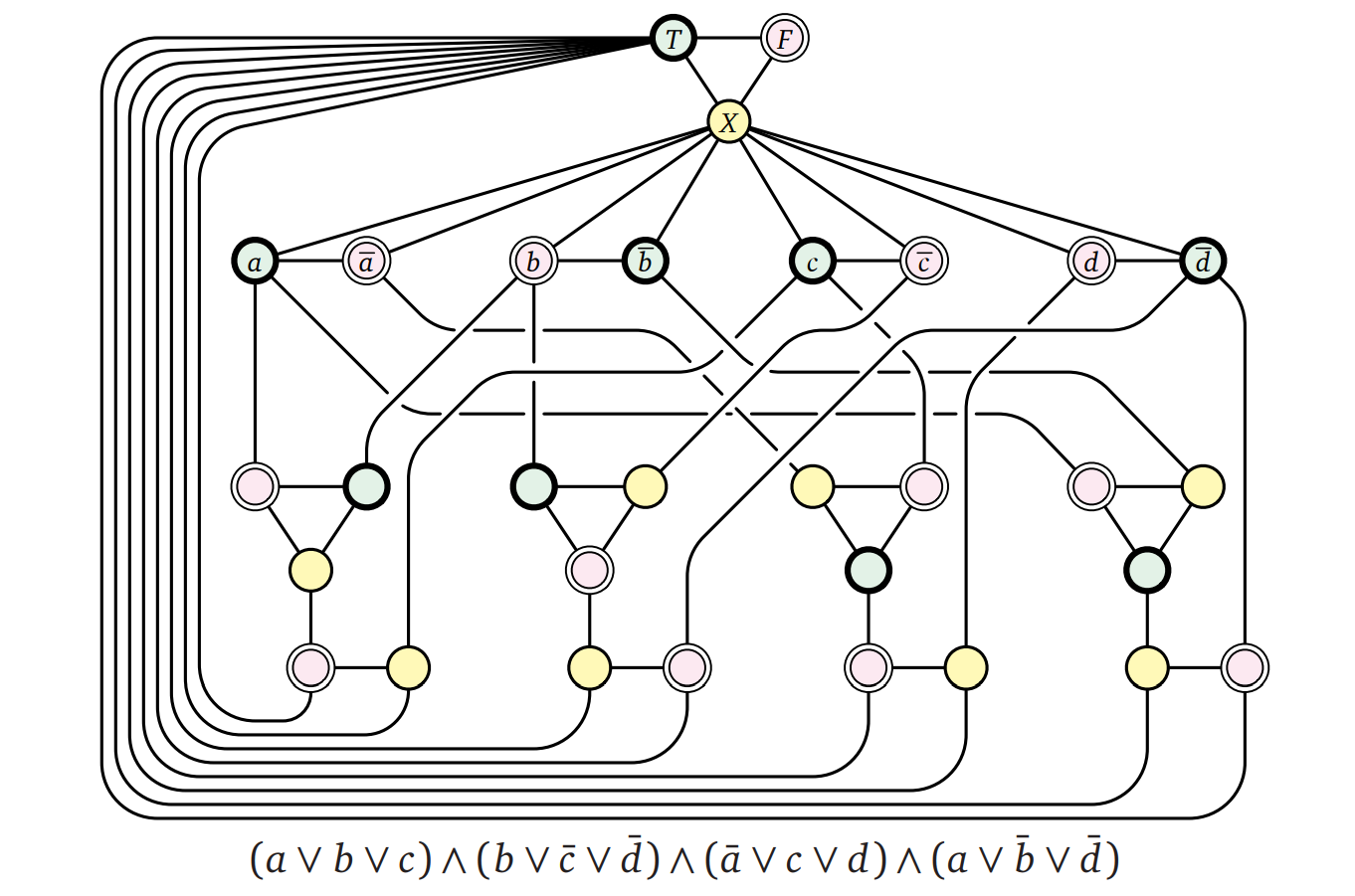
こうして出来上がるグラフの正しさの証明はこれまでにほぼ終わっています。式が充足可能ならば、任意の真偽値割り当てに基づいてリテラルの頂点を彩色でき、さらに (どの節にも \(\textsc{True}\) と \(\textsc{False}\) が少なくとも一つ含まれることから) その彩色を全ての節ガジェットに対する彩色に拡張できます。逆にグラフが 3-彩色可能ならば彩色から変数に対する真偽値割り当てを作ることができ、その割り当ては各節の少なくとも一つのリテラルを \(\textsc{True}\) にするので、全体の式を充足させます。
したがって \(\textsc{3Color}\) は NP 困難です。\(\textsc{3Color}\) は一般的な彩色問題 (「彩色に必要な色は最低何色?」) の特殊ケースなので、この一般的な最適化問題も NP 困難です。
-
例えば以前に示した \(\textsc{CircuitSAT}\) から \(\textsc{SAT}\) への帰着では各ゲートを論理式における節に変換しましたが、この帰着では節が "ゲートガジェット" となります。また \(\textsc{3SAT}\) から \(\textsc{MaxIndSet}\) への帰着では、節ガジェット (三角形) と変数ガジェット (矛盾する辺の間の辺) という二つのガジェットが登場しました。[return]