ハミルトン閉路

ハミルトン閉路 (Hamiltonian cycle) とはグラフの全ての頂点をちょうど一回ずつ訪れる閉路のことです (オイラー閉路 (Eulerian cycle) とは異なります。オイラー閉路は全ての辺をちょうど一回ずつ使う閉じた歩道であり、深さ優先探索を使って線形時間で簡単に見つけられます)。ここでは有向グラフに対するハミルトン閉路問題が NP 困難であることの証明を二つ示します。

頂点被覆からの帰着

ハミルトン閉路問題の NP 困難性の証明の一つ目は、判定バージョンの頂点被覆問題からの帰着を使うものです。この証明では与えられた無向グラフ $G$ と整数 $k$ から、有向グラフ $H$ であって $H$ にハミルトン閉路が存在するときに限って $G$ に大きさ $k$ の頂点被覆が存在するようなものを構成します。一つ前の帰着と同じように、出力のグラフ $H$ はいくつかのガジェットからなり、それぞれのガジェットが入力のグラフ $G$ と整数 $k$ の特徴を反映します。

$G$ の全ての無向辺 $uv$ に対して、$H$ は辺ガジェットとして頂点 $(u,v,\text{in})$, $(u,v,\text{out}) $, $(v,u,\text{in})$, $(v,u,\text{out}) $ およびその間の辺 \[ \begin{aligned} (u, v,\text{in}) & \rightarrow (u, v, \text{out})& (u, v,\text{in}) & \rightarrow (v, u,\text{in}) \\ (v, u,\text{in}) & \rightarrow (u, v,\text{in})& (v, u,\text{in}) & \rightarrow (v, u, \text{out}) \\ (u, v, \text{out}) & \rightarrow (v, u, \text{out})& (v, u, \text{out}) & \rightarrow (u, v, \text{out}) \end{aligned} \] を持つ。下図にあるように、これらの辺以外に "in" 頂点には入ってくる辺が、"out" 頂点には出ていく辺がある。ここで $H$ の任意のハミルトン閉路について、辺ガジェットの通り抜け方は三種類しかない。つまり、両方の道を別々に通るか、右の道から入って全ての頂点をたどるか、左の道から入って全ての頂点をたどるかである。

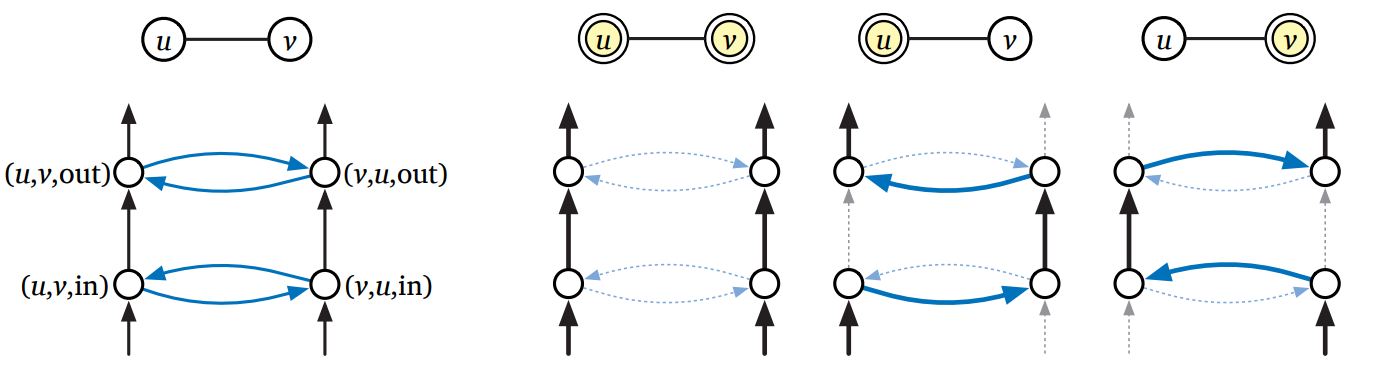図 12.13

辺ガジェットとそれを通り抜けるハミルトン閉路 (の一部)
$G$ の任意の頂点 $u$ について、$u$ に隣接する辺 $uv$ の辺ガジェットは $H$ において一つの有向路でつながれている。この辺ガジェットが連なったものを頂点鎖 (vertex chain) と呼ぶ。具体的に言うと、$u$ に隣接する頂点を $v_{1}, v_{2}, \ldots, v_{d}$ としたとき、 $H$ には $i = 1 \ldots d-1$ に対して $(u, v_{i}, \text{out})$ $\rightarrow$ $(u, v_{i+1}, \text{in})$ という辺がある。
$H$ には $k$ 個の被覆頂点 (cover vertex) $x_{1}, x_{2}, \ldots, x_{k}$ があり、各 $x_{i}$ には各頂点鎖の最初の頂点への辺、および各頂点鎖の最後の頂点からの辺がある。

この帰着の完全な例を次の図に示します。

図 12.14

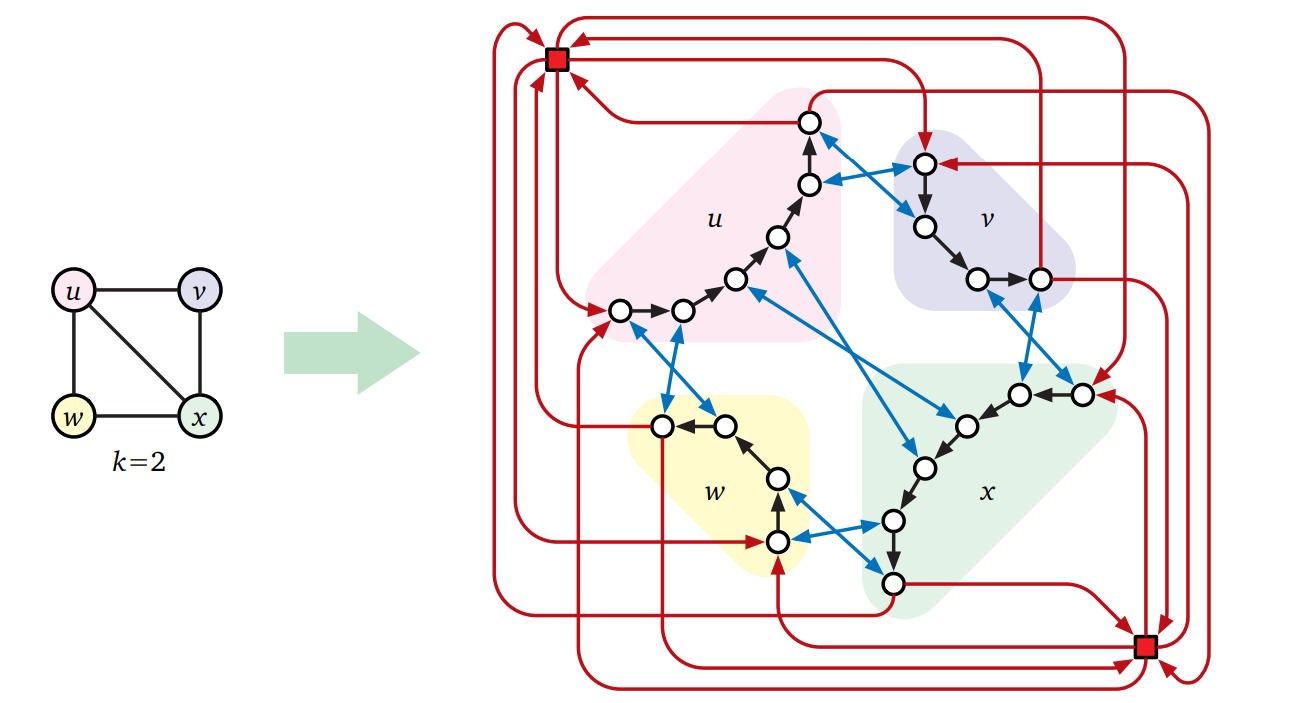
$\textsc{VertexCover}$ から $\textsc{HamiltonianCycle}$ への帰着

「$G$ に大きさ $k$ の頂点被覆がある $\iff$ $H$ にハミルトン閉路がある」の証明はいつも通り二つのステップからなります。

$(\Rightarrow)$ $C = \lbrace u_{1}, u_{2}, \ldots, u_{k} \rbrace$ が $G$ の頂点被覆であると仮定する。このとき次のようにして $H$ の閉路を構築する。閉路は $x_{1}$ から始まり、任意の添え字 $i = 1, \ldots, k$ について $x_{i}$ から $u_{i}$ の頂点鎖を通って $x_{i+1}$ に至る。$u_{i}$ の頂点鎖を通り抜けるとき、各頂点 $(u_{i}, v, \text{in})$ の次の頂点は次のように定める:
- $v \in C$ ならば $(u_{i}, v, \text{in}) \rightarrow (u_{i}, v, \text{out})$ と頂点鎖を素直にたどる。
- $v \notin C$ ならば $(u_{i}, v, \text{in}) \rightarrow$ $(v, u_{i}, \text{in}) \rightarrow$ $(v, u_{i}, \text{out}) \rightarrow$ $(u_{i}, v, \text{out})$ と迂回して頂点鎖をたどる。
$G$ の各辺 $uv$ について、こうして出来上がる閉路が $(u,v,\text{in})$ と $(u,v,\text{out})$ を訪れるのは、$u \in C$ ならば $u$ の頂点鎖をたどるときであり、$u \notin C$ ならば $v$ の頂点鎖をたどるときである。次の図も参照:

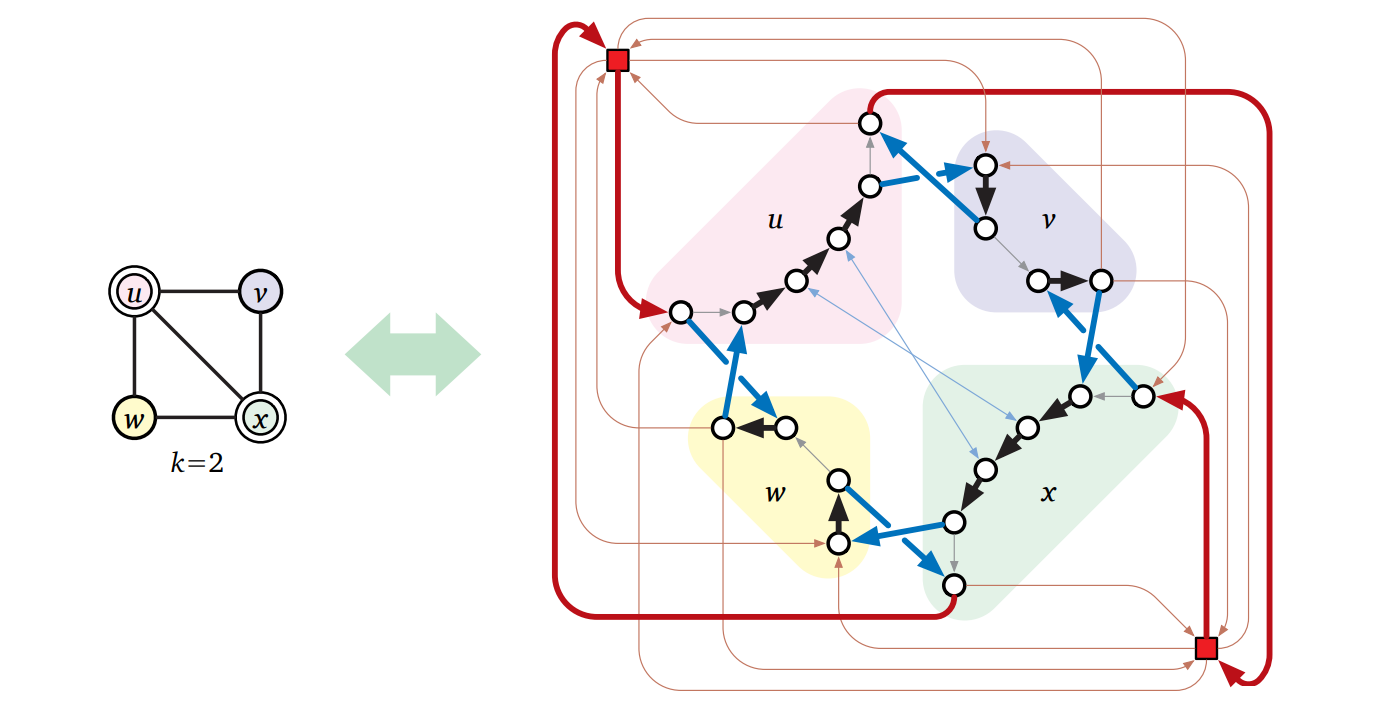$$G$ の大きさ $k$ の任意の頂点被覆は $H$ のハミルトン閉路に対応し、その逆も成立する$

図 12.15

$G$ の大きさ $k$ の任意の頂点被覆は $H$ のハミルトン閉路に対応し、その逆も成立する

$C$ が頂点被覆なことから、こうして出来上がる閉路は $H$ の辺ガジェットに含まれる頂点を全て訪れる。$H$ の被覆頂点以外の頂点は全ていずれかの辺ガジェットに含まれるから、この閉路はハミルトン閉路である。
$(\Leftarrow)$ $H$ にハミルトン閉路 $C$ が含まれるとする。$C$ には被覆頂点から頂点鎖の最初の頂点への辺が少なくとも一つ含まれる。ハミルトン閉路が辺ガジェットをどう通り抜けるかについての考察から、$C$ が頂点鎖に入ったときにはその頂点鎖から出てくることが帰納的に分かる。よって $(u,v,\text{in})$ という形の任意の頂点について、$C$ には $(u,v,\text{in}) \rightarrow (u, v, \text{out})$ という単一の辺または $(u, v, \text{in}) \rightarrow$ $(v, u, \text{in}) \rightarrow$ $(v, u, \text{out}) \rightarrow$ $(u, v, \text{out})$ という迂回路が含まれる。この辺または迂回路の後にあるのは $u$ が頂点鎖の最後の頂点である場合には被覆頂点であり、そうでない場合は $u$ の頂点鎖における次の辺ガジェットである。

ハミルトン閉路が辺ガジェットをどう通り抜けるかについての考察から、$C$ に迂回路 $(u, v, \text{in}) \rightarrow$ $(v, u, \text{in})$ が含まれるときには、$v$ の頂点鎖の端点と被覆頂点を結ぶ辺は $C$ に含まれないことが言える。よって $C$ が最初の頂点から入って最後の頂点から出る頂点鎖の数はちょうど $k$ 個である。$G$ の各辺 $uv$ について $C$ は $(u, v, \text{in})$ の形の頂点を全て訪れるので、$C$ が最初から最後まで通り抜ける頂点鎖に対応する頂点の集合は大きさ $k$ の頂点被覆となる。

以上より、「$G$ に大きさ $k$ の頂点被覆がある $\iff$ $H$ にハミルトン閉路がある」が言えます。$G$ から $H$ への変換には最大でも $O(n^{2})$ 時間しかかからないので、有向グラフに対するハミルトン閉路問題が NP 困難であることが分かります。

3SAT からの帰着

ハミルトン閉路問題の NP 困難性は 3SAT からの帰着を使っても示すことができます。与えられた 3CNF 式 $\Phi$ が $n$ 個の変数 $x_{1}, x_{2}, \ldots, x_{n}$ と $k$ 個の節 $c_{1}, c_{2}, \ldots, c_{k}$ を持つとし、$\Phi$ が充足可能なときに限ってハミルトン閉路を持つような有向グラフ $H$ をこれから構築します。

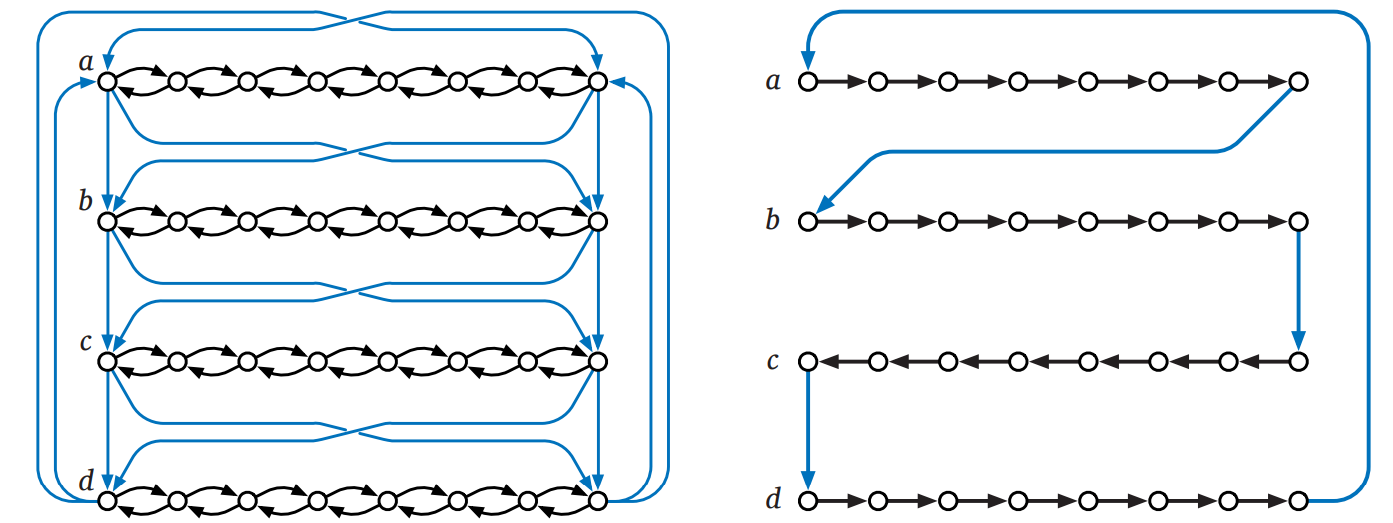
$H$ には $\Phi$ の各変数に対応する変数ガジェットが含まれます。変数 $x_{i}$ に対する変数ガジェットは $2k$ 個の頂点 $(i,0), (i,1), \ldots, (i,2k)$ を持ち、任意の添え字 $j$ について $(i, j-1) \rightarrow (i,j)$ および $(i, j) \rightarrow (i, j-1)$ という辺を持ちます。

さらに隣り合う変数ガジェットの最初と最後の頂点は辺で結ばれます。つまり任意の添え字 $i$ について \[ \begin{aligned} (i, 0) & \rightarrow (i+1, 0) & (i, 2k) & \rightarrow (i+1, 0) \\ (i, 0) & \rightarrow (i+1, 2k) & (i, 2k) & \rightarrow (i+1, 2k) \end{aligned} \] という辺が存在します。加えて最初と最後の変数ガジェットは次の辺で結ばれます: \[ \begin{aligned} (n, 0) & \rightarrow (1, 0) & (n, 2k) & \rightarrow (1, 0) \\ (n, 0) & \rightarrow (1, 2k) & (n, 2k) & \rightarrow (1, 2k) \end{aligned} \]

こうして出来上がるグラフ $G$ にはちょうど $2^{n}$ 個のハミルトン路が含まれ、それぞれが $\Phi$ の $n$ 個の変数に対する異なる真偽値割り当てに対応します。具体的には、$i$ 番目のガジェットを左から右にたどるなら $x_{i} = \textsc{True}$ であり、右から左なら $x_{i} = \textsc{False}$ です。次の図も参照してください:

図 12.16

左: $G$ における変数ガジェット右: $a = b = d = \textsc{True}$, $c = \textsc{False}$ という真偽値割り当てに対応する $G$ のハミルトン閉路

$\Phi$ の各節 $c_{j}$ に対応する節ガジェットを $G$ に加えることで $H$ を作ります。節 $c_{j}$ に対応する節ガジェットには一つの頂点 $[j]$ が含まれ、$[j]$ と変数ガジェットの間には次の図に示すような 6 本の辺が存在します。つまり、$c_{j}$ の正のリテラル $x_{i}$ に対しては辺 $(i, 2j - 1) \rightarrow$ $[j] \rightarrow$ $(i, 2j)$、$c_{j}$ の負のリテラル $\overline{x}_{j}$ に対しては $(i,2j) \rightarrow$ $[j] \rightarrow$ $(i, 2j - 1)$ です。

図 12.17

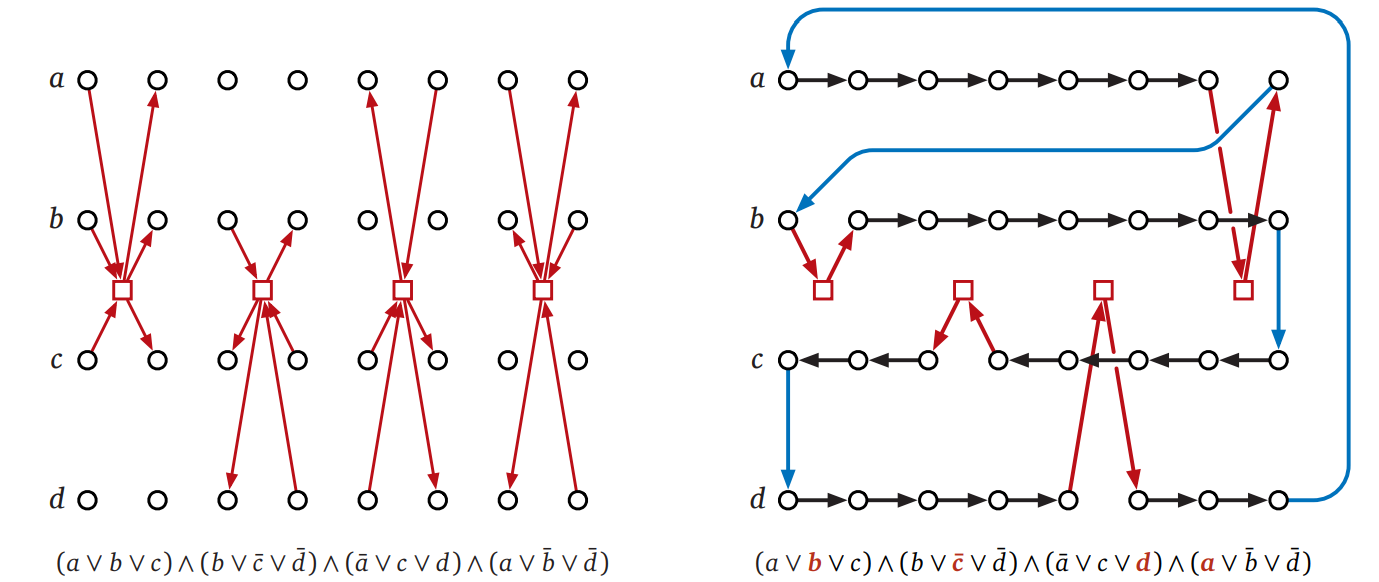
左: $H$ に含まれる節ガジェット右: $a = b = d = \textsc{True}$, $c = \textsc{False}$ という $\Phi$ を充足させる真偽値割り当てに対応する $H$ のハミルトン閉路

節ガジェットの辺の構成から、$G$ のハミルトン閉路が $H$ のハミルトン閉路に拡張できるのは対応する真偽値割り当てが $\Phi$ を充足させるときに限られることが言えます。しらみつぶしに場合分けをしていけば、「$H$ がハミルトン閉路を持つ $\iff$ $\Phi$ が充足可能」が示せます。

論理式 $\Phi$ を $H$ に変換するには $O(kn)$ の時間かかりますが、これは最大でも $\Phi$ の全長の二次式です。よって有向グラフに対するハミルトン閉路問題が NP 困難であると結論できます。

変種と拡張

前述の帰着を少し変更すると、ハミルトン "路" 問題が NP 困難であることも示せます。ここで $G$ のハミルトン路とはもちろん $G$ の全ての頂点をちょうど一回ずつ通る単純路のことです。実は $\textsc{HamiltonianCycle}$ と $\textsc{HamiltonianPath}$ の間には多項式時間帰着が双方向に存在します。どちらの帰着も簡単なので、詳細は練習問題とします。

この節で説明した二つの帰着はどちらも有向グラフを扱っていますが、無向グラフに対するハミルトン閉路問題も NP 困難です。実は有向グラフに対するハミルトン閉路問題から無向グラフに対するハミルトン閉路問題への簡単な帰着が存在します。この帰着の詳細も楽しい練習問題とします。

最後に、悪名高き巡回セールスマン問題 (traveling salesman problem) は辺に重みの付いたグラフにおける最短のハミルトン閉路 (または路) を見つける問題と言えます。最短の閉路/路を見つけるのは閉路/路が存在するかを判定するよりも明らかに難しい ――辺の重みが全て $1$ のグラフを考えてみてください！―― ので、巡回セールスマン問題も同じく NP 困難です。