NP 困難・NP 容易・NP 完全

問題 \(\Pi\) がNP 困難 (NP-hard) であるとは、\(\Pi\) に対する多項式時間合アルゴリズムが NP に属する全ての問題に対する多項式時間アルゴリズムを意味することを言います。言い換えると:

\(\pmb{\Pi}\) が NP 困難 \(\iff\) \(\pmb{\Pi}\) が多項式時間で解けるなら P=NP

分かりやすく言うと、ある NP 困難な問題 \(\Pi\) が一つでも高速に解ければ、 \(\Pi\) を解くサブルーチンを使うことで、答えが簡単に検証できる種類の問題全てを高速に解くことができるということです。NP 困難な問題は少なくとも NP に属する全ての問題以上に難しいと言えます。

そして問題が NP 完全 (NP complete) であるとは、NP 困難かつ NP に属する ("NP 容易である") ことを言います。くだけて言うと、NP 完全な問題とは NP の中で一番難しい問題です。ある NP 完全な問題に対する多項式時間アルゴリズムがあれば、全ての NP 完全な問題に対する多項式時間アルゴリズムが直ちに手に入ります。数千個もの問題が NP 完全であると示されているので、その中のある一つの問題に対する (そして全ての問題に対する) 多項式時間アルゴリズムというのはまずありえなさそうに思えるわけです。

ある問題が NP 困難であると示すのは、「もし私が犬を飼っているなら、私の犬は英語を流暢に話す」と言うようなものです。私が犬を飼っているかあなたには分からないでしょうが、英語を話す犬を飼っていないことは分かるはずです。犬が英語を話せないことの数学的な証明はありません ――英語を話す犬を誰も見たことがないこと、あるいは犬に英語を話すための器官や脳が足りていないことを示すたくさんの研究結果も証拠に過ぎず、証拠だけでは数学的な証明にはならないからです。しかしもちろんまともな人間ならば私が流暢に英語を話す犬を飼っているとは信じないので、「もし私が犬を飼っているなら、私の犬は英語を流暢に話す」という文章からは、「まともな人間は私が犬を飼っているとは信じない」という系が得られます！同様に、ある問題が NP 困難ならば、まともな人間はその問題が多項式時間で解けるとは思いません。

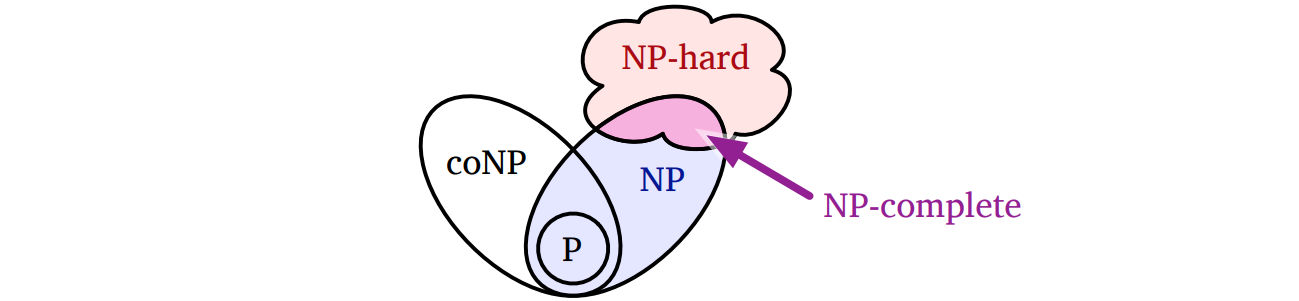
どんな問題であれ、その問題が NP 困難かどうかは自明ではありません。次に示す重要な定理は 1971 年に Steve Cook (スティーブ・クック) によって発表され、その後 1973 年には Leonid Levin (レオニード・レビン) によって独立に示されています¹。ここまで定義を (意図的に) 曖昧に書いてきたので、証明は省略します²。

Cook-Levin の定理: 回路充足問題は NP 困難。

Levin は自身の結果を 1971 年にモスクワで行われたセミナーで発表しており、そのときはまだ Ph.D. 生でした。Cook による証明の報は少なくとも 1973 年になるまでソ連に届かず、届いたのは Levin が自身の結果を発表した後のことでした。スティグラーの法則に従って、この結果は "Cook の定理" と呼ばれることが多いです。Levin は政治的理由によりモスクワ大学での Ph.D. を拒否され、1978 年にはアメリカに移住し、翌年 MIT で Ph.D. を取得しています。Cook は世界的な影響力を持つことになる論文を発表するわずか一年前の 1970 年にカリフォルニア大学バークレー校のテニュア職を断られています。Cook はこの証明によってチューリング賞を受賞しました (Levin は受賞しませんでした)。^[return]
もし興味があるなら、http://algorithms.wtf にある非決定性チューリング機械に関する講義ノート、あるいは Boaz Barak による素晴らしいプロジェクト Introduction to Theoretical Computer Science を見てください^[return]