帰着と SAT

回路充足性問題以外の全ての問題に対する NP 困難性を証明するには、帰着を使った議論が必要になります。問題 A を別の問題 B に帰着させる (reduce problem A to anther problem B) とは、問題 B へのアルゴリズムが手に入っているという仮定の下で問題 A を解くアルゴリズムを説明することを言います。帰着はこの本を読み始める前にも何度も行ってきたはずですが、そのときには帰着のことを「サブルーチンを書く」あるいは「ユーティリティ関数を書く」または「モジュール性の高いプログラムを書く」ときには「電卓を使う」などと呼んでいたでしょう。ある問題が NP 困難であることを示すときにもこれと同じような問題の間の変形を行いますが、ほとんどの人が想像する方向とは逆方向の変形を行います。

次の文章をタトゥーにして、腕の内側、ママの誕生日とモノポリーの本当のルール¹の横に刻んでおくべきです。

問題 A が NP 困難であることを証明するには、

既知の NP 困難な問題を A に帰着させる。

つまり、ある問題が難しいことを示すには、その問題を効率良く解く正体不明のアルゴリズムをブラックボックスのサブルーチンとして仮定して、難しいことが前もって分かっている別の問題を解くアルゴリズムを示すことになります。ここで本質的に使われている論理は背理法による証明です。つまり、もし考えている問題が簡単ならもう一方の問題も簡単だと帰着が示しているのですが、それはあり得ないと最初から分かっているということです。同じことを言い換えると、もう一方の問題が難しいと分かっているので、帰着によって今考えている問題も難しい、つまり仮定として置いた効率の良いアルゴリズムは存在しないと示されるのです。

単純で重要な例として、式充足性問題 (formula satisfiability problem, $\textsc{SAT}$) を考えます。$\textsc{SAT}$ の入力は次のようなブール式: \[ (a \lor b \lor c \lor \overline{d}) ⇔ ((b \land \overline{c}) \lor \overline{(\overline{a} ⇒ d)} \lor (c \neq a \land b)) \] であり、出力はこの式の変数 $a, b, \ldots, $ に真偽値を割り当てて式全体を $\textsc{True}$ にできるかどうかです。

$\textsc{SAT}$ が NP 困難であることを示すには、既知の NP 困難な問題からの帰着を示す必要があります。私たちがこれまでに NP 困難であることを見た問題は $\textsc{CircuitSAT}$ だけなので、そこから始めましょう。

$K$ を任意のブール回路とします。$K$ の各ゲートに新しい変数を割り当てて、ゲートごとに入出力を $=$ でつないだ式をさらに $\textsc{And}$ でつなげば $K$ をブール式に変換できます。次の図にこの例を示します。

続いて元の回路 $K$ の充足可能性とこの変換で得られる式 $\Phi$ の充足可能性が同値であることを示します。同値性の証明でよくあるように、証明は二つのステップからなります:

$(\Rightarrow)$ $K$ を充足させる入力が与えられれば、$K$ の各ゲートにおける出力の値を計算することで $\Phi$ を充足させる変数への真偽値割り当てを得られる。
$(\Leftarrow)$ $\Phi$ を充足させる変数割り当てが与えられれば、中間の変数 $y_{i}$ と最終的な出力 $z$ を無視することで $K$ を充足させる入力を得られる。

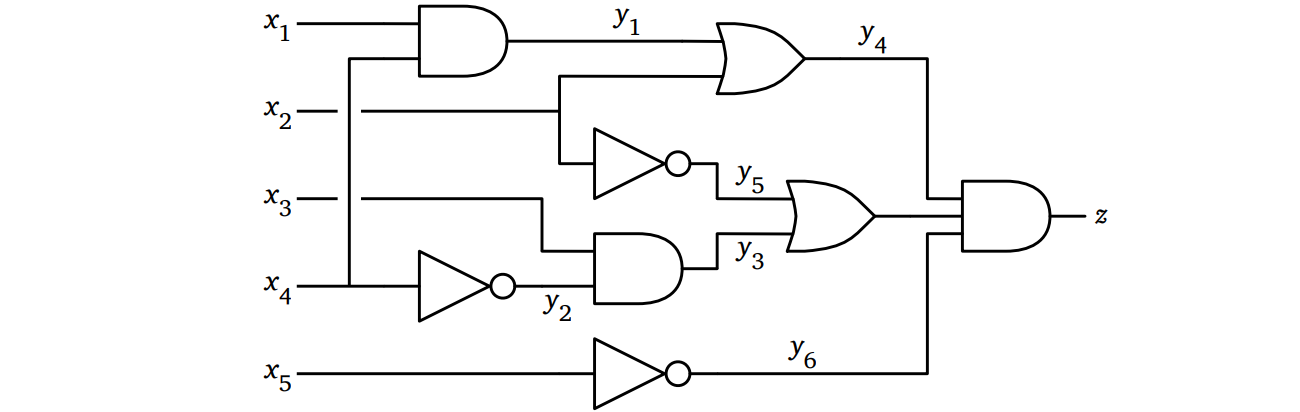
\[ \begin{aligned} & (y_1 = x_1 \land x_4) \land (y_2 = x_4) \land (y_3 = x_3 \land y_2) \land (y_4 = y_1 \lor x_2) \land {}\\ & (y_5 = x_2) \land (y_6 = x_5) \land (y_7 = y_3 \lor y_5) \land (z = y_4 \land y_7 \land y_6) \land z \end{aligned} \]

論理回路を論理式に変換する

回路からブール式への変換は線形時間で行うことができ、変換結果のブール式の大きさは常識的な方法で表された回路の大きさの高々定数倍です。

与えられたブール式が充足可能かどうかを多項式時間で判定するアルゴリズムが存在すると仮定します。このときブール回路 $K$ が与えられれば、上記の方法で $K$ をブール式 $\Phi$ に変形し、この $\Phi$ に対してその正体不明の $\textsc{SAT}$ アルゴリズムを適用することで、$K$ が充足可能かどうかを判定できます。

この処理を次の図に示します。四角がアルゴリズムを表し、左の赤い四角が変形のためのサブルーチンを、右の水色の四角が正体不明の $\textsc{SAT}$ アルゴリズムを表します。虹がかかっているのですから、魔法の箱に決まっています²。

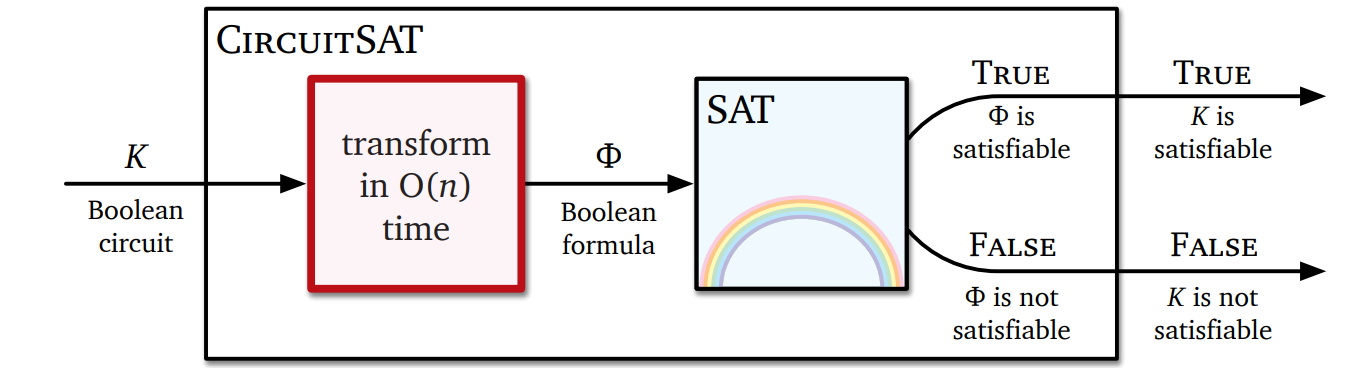
魔法の箱ではなく魔法の疑似コードがお好みなら:

procedure $\texttt{CircuitSAT}$($K$)

$K \text{ をブール式 } \Phi \text{ に変換する}$

return $\texttt{SAT}$($\Phi$) ${\color{maroon}\langle \langle} *** \color{orange}{M} \color{olive}{A} \color{green}{G} \color{teal}{I} \color{#2D2F91}{C} *** {\color{maroon}\rangle \rangle}$

$K$ を $\Phi$ に変換する処理は多項式時間で行える (本当は線形時間なのですが、多項式時間でできることは確かな) ので、$\textsc{CircuitSAT}$ アルゴリズム全体も多項式時間で実行できます: \[ T_{\textsc{CircuitSAT}}(n) \leq O(n) + T_{\textsc{SAT}}(O(n)) \] よって $\textsc{SAT}$ に対する多項式時間アルゴリズムがあれば $\textsc{CircuitSAT}$ に対する多項式時間アルゴリズムが手に入り、したがって P=NP です。すなわち $\textsc{SAT}$ は NP 困難です！

売られている不動産のマスに止まったプレイヤーがその不動産を買うことを拒否した (あるいは買うだけの金が無い) 場合、不動産は競売にかけられる。最初に不動産を買うことを拒否したプレイヤーも競売に参加でき、競売の結果の値段は元の値段より高くも低くもなりうる。刑務所にいるプレイヤーも不動産、家、ホテルの売買および家賃の徴収を行ってよい。ゲームには 32 の家と 12 のホテルがある。それらが無くなったら、無くなる。特に全ての家が既にボード上にあるときにはホテルを 4 つの家にダウングレードさせることができず、取り壊すことしかできない。プレイヤーは未開発の不動産を他のプレイヤーと交換したり売ったりできるが、銀行に売り戻すことはできない。無料駐車場に止まったプレイヤーは何も得られない。Go に止まったプレイヤーはちょうど $200 を得る。鉄道は魔法の輸送機関でない。そして最後に、Jeff は必ず長靴を手に入れる。T-Rex でもペンギンでもなく ――長靴、クソッ。^[return]
Kate Erickson, personal communication, 2011. 白黒のバージョンを読んでいる人へ: 丸くなっているものは虹です。^[return]