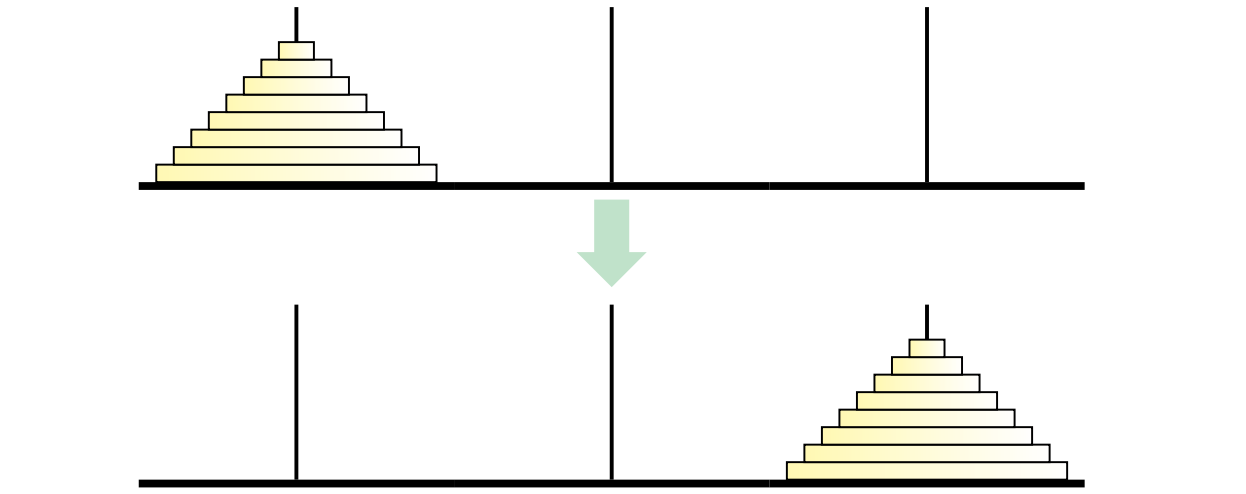
再帰

孫子曰わく、およそ衆を治むること寡を治むるがごとくなるは、分数これなり。

――孫武, 『孫氏』 (紀元前 400 年ごろ)

人生はこまごましたことで削られていく... 単純に、単純に。

――Henry David Thoreau, Walden (1854)

Voom が何かなんて聞かないでくれ、分かりっこないんだから。

でも待った、雪を掃除することは知ってるぞ！

――Dr. Seuss [Theodor Seuss Geisel], The Cat in the Hat Comes Back (1958)

難しい仕事を先にやれ。簡単な仕事は放っておいても消えていく。

――Dale Carnegie

帰着

帰着 (reduction) はアルゴリズムを設計するときに最もよく使われるテクニックです。問題 $X$ を問題 $Y$ に帰着させると言った場合、それは $Y$ を解くアルゴリズムをブラックボックス (サブルーチン) として使いながら $X$ を解くことを意味します。帰着を考えるときに重要なのが、帰着の結果として出来上がる $X$ を解くアルゴリズムの正しさを、ブラックボックスがどう問題 $Y$ を解くかに依存させてはいけない点です。仮定してよいのは、ブラックボックスが $Y$ を正しく解くということだけです。中で起こっていることは私たちには関係なく、誰か別の人の問題です。ブラックボックスが文字通り魔法によって動くと考えるとよいでしょう。

例えば前章で説明した農民の掛け算アルゴリズムは、正の整数の掛け算という問題を、足し算、mediation、パリティ検査という三つの簡単な問題に帰着させます。アルゴリズムは "正の整数" という抽象的なデータ型を今あげた三つの演算をサポートするものとして定義していますが、乗算アルゴリズムの正しさは正の整数の表現 (画線法、クレイトークン、バビロニアの六十進法、キープ、算木、ローマ数字、指、augrym stones、ゴバール数字、二進法、負の二進法、グレイコード、平衡三進法、黄金進法、四分虚数進法) や演算の実装方法に依存していません。もちろん乗算アルゴリズムの実行時間は足し算、mediation、パリティ検査の実行時間によって変わります。しかしこれは正しさとは別の問題です。最も重要なこととして、帰着を考えておけば数字の表現を変えるだけで効率の良いアルゴリズムを得ることができます (画線法から位取り記数法に変える、のように)。

同様に Huntington-Hill のアルゴリズムは、下院議会の議席配分の問題を、 $\textsc{Insert}$ と $\textsc{ExtractMax}$ をサポートする優先度付きキューを管理することに帰着しています。ここで抽象データ型 "優先度付きキュー" はブラックボックスになっていて、配分アルゴリズムの正しさは優先度付きキューの特定の実装を仮定していません。もちろん、このアルゴリズムの実行時間は $\textsc{Insert}$ と $\textsc{ExtractMax}$ の実行時間によって変わります。しかしこれは正しさとは別の問題です。帰着が優れているのは、優先度付きキューといったデータ型の実装を効率の良いものに取り換えることで効率の良い配分アルゴリズムを得られる点です。さらに、優先度付きキューというデータ型の設計者はそのデータ型が下院議席の配分で使われることを気にせずに済みます。

アルゴリズムで使われている基本的な部品がどのように実装されているか、あるいは設計しているアルゴリズムがさらに大きな問題を解くときにどのような部品として使われるかを正確に知るのは不可能です。これは初心者にとって落ち着かないことかもしれませんが、これは避けられないばかりか、とても有用なことでもあります。アルゴリズムの中の部品がどう動くかを正確に知っているときでさえ、細部を無視することはとても有用です。

単純にして任せる

再帰 (recursion) は特に強力な帰着です。大雑把に言うと、次のように説明できます:

もし問題のインスタンスを直接解くことができるなら、直接解く。
そうでなければ、問題を同じ問題のよりシンプルなインスタンスに帰着させる。

自分自身を参照する部分が分かりにくいなら、他の帰着と同じように、小さいインスタンスを別の人が解いてくれると想像するとよいでしょう (この別の人のことを再帰の妖精 (Recursion Fairy)と呼ぶのが私のお気に入りです)。問題を解くためにすべきなのは、問題を単純にする、あるいはそれが不必要/不可能な場合には直接解く、それだけです。小さくなった問題は再帰の妖精が解いてくれます。どうやって解くかは私たちの知ったことではありません¹。数学をよく知っている読者は再帰の妖精のことをもっと正式な名前で呼ぶかもしれません: 帰納法の仮定と。

再帰的な手続きが正しく動くためには、ある簡単な条件を満たす必要があります: 単純なインスタンスをたどっていったときに無限列ができてはいけません。つまり、再帰的な帰着はいずれベースケースにたどり着かなければなりません。ベースケースとは再帰でない方法で解ける簡単なインスタンスのことです。もしベースケースが存在しなければ、再帰的なアルゴリズムは永遠にループしてしまいます。この条件を満たすために最もよく使われるのは、問題を (複数の) 小さなインスタンスに帰着させる方法です。例えば $n$ 個の頭を持つドラゴンを倒す再帰的な戦略を考えているとしましょう。このとき、再帰的に呼ぶ問題は頭の数が $n$ 個より真に小さいドラゴンに対する問題である必要があります。もちろん $n=0$ でドラゴンが頭を持っていないときには再帰的な呼び出しができなくなる ――頭の数が負のドラゴンは存在しません！―― ので、この場合は頭の無いドラゴンを直接倒すことになります。

再帰の例は農民の掛け算アルゴリズムで既に出てきています。つまり、次の再帰的な等式 (再帰方程式) です: \[ x \times y = \begin{cases} 0 & \text{if } x = 0 \\ \lfloor x / 2 \rfloor \times (y + y) & \text{if } x \text{ が偶数} \\ \lfloor x / 2 \rfloor \times (y + y) + y & \text{if } x \text{ が奇数} \\ \end{cases} \] この再帰方程式はアルゴリズムとして次のようにも表現できます:

procedure $\texttt{PeasantMultiply}$($x, y$)

if $x = 0$ then

return $0$

else

$ x^{\prime} \leftarrow \lfloor x/2 \rfloor $

$ y^{\prime} \leftarrow y + y $

$ \mathit{prod} \leftarrow $$\texttt{PeasantMultiply}$($x^{\prime}, y^{\prime}$) $\quad$ ⟨⟨再帰！⟩⟩

if $x$ が奇数 then

$ \mathit{prod} \leftarrow \mathit{prod} + y $

return $\mathit{prod}$

怠惰なエジプトの書記官がこのアルゴリズムを実行するときは、まず $x^{\prime}$ と $y^{\prime}$ を計算し、部下の書記官に $x^{\prime}$ と $y^{\prime}$ の積を計算するように頼み、最後に必要ならば部下からの答えに $y$ を足して終わります。$x^{\prime} < x$ であり、単調に減少する正の整数の数列はいずれ $0$ になることから、部下に渡される問題はより単純なものだと言えます。部下が $x^{\prime} \cdot y^{\prime}$ をどう計算するかは上司の知ったことではありません (あなたが気にする必要もありません)。

Hanoi の塔

Hanoi (ハノイ) の塔は 1883 年²にフランス人教師で娯楽数学者でもあった Éduoard Lucas (エドゥアール・リュカ) によって³最初に発表されました ――実際に遊べるパズルとして！その次の年、Henri de Parville (アンリ・ド・パルヴィル) はこのパズルを次のストーリーと共に紹介しています⁴:

Benares (ベナレス) にある大寺院⁵...世界の中心にあるドームには、三つのダイアモンドの棒が刺さった真鍮のプレートがある。棒の高さは 1 キュービット (約 50 cm) であり、太さはハチの体ほどである。この世を創生するときに、神は 64 個の金の円盤を棒の一つに通して置いた。そのとき神は一番大きな円盤が真鍮のプレートと接するように、そして上に行けば行くほど円盤が小さくなるようにした。これが Bramah (ブラマー) の塔である。司祭たちは昼夜とめどなく円盤をひとつの棒から他の棒に移動させる。円盤を移動させるとき、司祭たちは絶対の Bramah の法に従う。つまり、円盤は必ずひとつずつ移動させなければならず、ある円盤の下にそれよりも小さい円盤があるようにすることはできない。 64 個の円盤を神が創生のときに使った棒から別の棒に全て移動させることができたならば、塔、寺院、そして Brahmin (バラモン) は塵となり、雷鳴と共に世界は消えてしまうという。

私たちは善き計算機科学者として、この物語に出現する定数 64 を変数 $n$ で置き換えます (当然です)。それから物理的なパズルは通常ダイアモンドと金ではなく木でできているので、円盤を入れる場所のことを棒ではなく杭と呼ぶことにします。三番目の杭を一時的な置き場所として使いながら、円盤を自身よりも小さい円盤の上に置くことなく、$n$ 個の円盤を二番目の杭に移動させるにはどうすればよいでしょうか？

N. Claus de Siam もパズルに付いてくるパンフレットで語っていることですが、このパズルを解く鍵は再帰的に考えることにあります。パズル全体を一度に解こうと考えるのをやめて、まず一番大きい円盤を動かすことに集中しましょう。最初の状態では一番大きい円盤の上には他の全ての円盤が載っているので、この円盤を動かすことはできません。そのため最初に $n - 1$ 個のディスクを一時的な置き場所の杭に移動させる必要があります。それから一番大きな円盤を目標の杭に移動させ、最後に $n-1$ 個の円盤をその上に移動させれば良いことになります。

さて、次に行うべきは――

違う！待て！

もうこれですべきことは終わっています！円盤が $n$ 個のHanoi の塔の問題を円盤が $n-1$ 個のHanoi の塔の問題を二回使って解くことができたので、あとは再帰の妖精 (Lucas の比喩を借りるなら "寺院の新人僧侶") に任せることができます。私たちの 仕事はこれで終わりです。信用できない僧侶が雇われるはずはありませんから、新人僧侶にあれこれ言うのはやめましょう。

この帰着にはとても重要で気付かれにくい仮定があります。一番大きい円盤の存在です。この再帰的なアルゴリズムは円盤の数が正のときだけ上手く動き、$n = 0$ のときには処理を行うことができません。幸い Benares の僧侶は敬虔な仏教徒なので、全く苦労せずにゼロ個の円盤をある杭から別の杭に移動させることができます: 何もしなければいいのです。

図 1.3

Hanoi の塔のアルゴリズムに対する空のケース。 There is no spoon.

パズルを解く中で他の小さい円盤がどう動くのか、あるいはもっと一般的に再帰的な手続きが展開されたときに何が起こるのかを知りたくなるかもしれません。それでも、どうか踏みとどまってください。ほとんどの再帰的なアルゴリズムにおいて、再帰を展開することは必要でもありませんし、理解に役立つわけでもありません。すべきことは、問題のインスタンスをより単純なインスタンスに帰着させる、それが不可能ならば直接解く、それだけです。Hanoi の塔のアルゴリズムは $n=0$ のとき明らかに正しく、そして $n \geq 1$ のときには再帰の妖精が上にある $n - 1$ 個の円盤動かしてくれるので (きちんと言うと、帰納法の仮定よりこの再帰的なアルゴリズムは $n-1$ 個の円盤を正しく移動させるので)、このアルゴリズムは任意の $n$ に対して正しいことが分かります。

Hanoi の塔のアルゴリズムは次のように表されます。このアルゴリズムは $n$ 個の円盤を元々あった杭 $\mathit{src}$ から目的地の杭 $\mathit{dst}$ へ、三番目の杭 $\mathit{tmp}$ を一時的な置き場所として使いながら移動させます。このアルゴリズムは $n=0$ のときにも正しいことに注意してください。

procedure $\texttt{Hanoi}$($ n,\mathit{src},\mathit{dst},\mathit{tmp} $)

if $ n > 0 $ then

$\texttt{Hanoi}$($n - 1, \mathit{src}, \mathit{tmp}, \mathit{dst}$) $\quad$ ⟨⟨再帰！⟩⟩

円盤 $n$ を $\mathit{src}$ から $\mathit{dst}$ へ移動させる

$\texttt{Hanoi}$($n - 1, \mathit{tmp}, \mathit{dst}, \mathit{src}$) $\quad$ ⟨⟨再帰！⟩⟩

図 1.4

Hanoi の塔パズルを解く再帰アルゴリズム

$n$ 個の円盤を移動させるのにかかる時間 ――このアルゴリズムの実行時間―― を $T(n)$ とします。$n = 0$ のときは何もしないので、 $T(0) = 0$ です。そして一般の $n \geq 1$ に対するアルゴリズムから、$T(n) = 2T(n-1) + 1$ が分かります。いくつかの $n$ について実際に値を計算すると、 $\pmb{T(n) = 2^{n} - 1}$ であることが予想でき、単純な帰納法によってこの答えの正しさが証明できます。

64 個の円盤を移動するのにかかる移動の回数を実際に計算すると、$2^{64}-1 =$ $18,\allowbreak446,\allowbreak446\allowbreak744,\allowbreak073,\allowbreak709,\allowbreak551,\allowbreak615$ 回となります。一秒に一回というとても速いスピードで円盤を動かしたとしても、 Brahmin が塵となり、雷鳴と共に世界が消えるまでには、Benares の僧侶は 5850億年 ("plus de cinq milliards de siècles") の間働き続けなくてはいけません。

マージソート

マージソート (mergesort) はプログラム内蔵式の汎用コンピューター用に作られた最も古いアルゴリズムの一つです。このアルゴリズムは John von Neumann (ジョン・フォン・ノイマン) によって 1945 年に開発され、 1947 年に Herman Goldstine (ハーマン・ゴールドスタイン) との共著で発表されました。このプログラムは EDVAC 用に作られた計算用途ではないプログラムのうち最初期のものでもあります⁶。マージソートは次のステップからなります:

入力の配列をほぼ同じ長さの二つの小配列に分割する。
二つの小配列に再帰的にマージソートを行う。
ソートされた二つの小配列をひとつの配列に組み合わせる (マージする)。

\[ \begin{array}{rc} \text{入力} :& \texttt{S O R T I N G E X A M P L} \\ \text{分割} :& \texttt{S O R T I N | G E X A M P L} \\ \text{左の再帰} :& \texttt{I N O R S T | G E X A M P L} \\ \text{右の再帰} :& \texttt{I N O R S T | A E G L M P X} \\ \text{マージ} :& \texttt{A E G I L M N O P R S T X} \end{array} \]

図 1.5

マージソートの例

最初のステップは配列の長さを $2$ で割るだけで済むので簡単です。二つ目のステップは再帰の妖精に任せることができます。そのため本当の作業と呼べるのは最後のマージのステップだけです。

完全なマージソートのアルゴリズムを次に示します。再帰的な構造を明らかにするために、マージのステップをサブルーチンとして別にしています。$\textsc{Merge}$ も再帰的なことに注意してください。最初に出力の先頭の要素を見つけ、それから残りの入力を再帰的にマージしています。

procedure $\texttt{MergeSort}$($ A[1..n] $)

if $ n > 1 $ then

$ m \leftarrow \lfloor n/2 \rfloor $

$\texttt{MergeSort}$($ A[1..m] $) $\quad \hphantom{{},+1}$ ⟨⟨再帰！⟩⟩

$\texttt{MergeSort}$($ A[m+1..n] $) $\quad$ ⟨⟨再帰！⟩⟩

$\texttt{Merge}$($ A[1..n], m $)

procedure $\texttt{Merge}$($A[1..n], m$)

$ i \leftarrow 1;\ j \leftarrow m+1 $

for $ k \leftarrow 1 $ to $ n $ do

if $ j > n $ then

$ B[k] \leftarrow A[i];\ i \leftarrow i + 1 $

else if $ i > m $ then

$ B[k] \leftarrow A[j];\ j \leftarrow j + 1 $

else if $ A[i] < A[j] $ then

$ B[k] \leftarrow A[i];\ i \leftarrow i + 1 $

else

$ B[k] \leftarrow A[j];\ j \leftarrow j + 1 $

for $ k \leftarrow 1 $ to $ n $ do

$ A[k] \leftarrow B[k] $

図 1.6

マージソート

正しさ

このアルゴリズムが正しいことを示すには、長い付き合いである帰納法を二回適用します。最初は $\textsc{Merge}$ サブルーチンに適用してから、次にトップレベルの $\textsc{MergeSort}$ アルゴリズムに適用します。

命題 1.1 小配列 $A[1..m]$ と $A[m+1..n]$ が正しくソートされているならば、$\textsc{Merge}$ は二つの小配列を正しくマージする。

証明 $A[1..n]$ を任意の配列、 $m$ を小配列 $A[1..m]$ と $A[m+1..n]$ がソートされているような任意の整数とする。0 から $n$ までの任意の $k$ について、$\textsc{Merge}$ の残り $n - k - 1$ 回のメインループが $A[i..m]$ と $A[j..n]$ を $B[k..n]$ に正しくマージすることをこれから示す。証明はこれからマージする要素の数 $n - k + 1$ に関する帰納法で行う。

$k > n$ ならば二つの小配列は空なので、何もしないことでマージが完了する (これが帰納法の証明のベースケースである)。そうでない場合、メインループの $k$ 回目の反復には 4 つの場合がある。

$j > n$ なら小配列 $A[j..n]$ は空なので $\min \left(A[i..m] \cup A[j..n] \right) = $ $A[i]$
$i > m$ なら小配列 $A[i..m]$ は空なので $\min \left(A[i..m] \cup A[j..n] \right) = $ $A[j]$
それ以外の場合で $A[i] < A[j]$ ならば $\min \left( A[i..m] \cup A[j..n] \right) = A[i]$
それ以外の場合 $A[i] \geq A[j]$ だから $\min \left( A[i..m] \cup A[j..n] \right) = A[j]$

四つの場合全てにおいて、$B[k]$ には $ A[i..m] \cup A[j..n] $ の最小の要素が代入される。$B[k] \leftarrow A[i]$ という代入が起こる二つの場合では、再帰の妖精、おっと、帰納法の仮定より残りの $n - k$ 回のメインループで $A[i+1..m]$ と $A[j..n]$ が $B[k+1..n]$ にマージされる。同様に残りの二つの場合でも帰納法の仮定より小配列は正しくマージされる。 $\Box$

定理 1.2 $\textsc{MergeSort}$ は入力の配列 $A[1..n]$ を正しくソートする。

証明 $n$ に関する帰納法で示す。$n \leq 1$ のときアルゴリズムは何もしないが、これは正しい動作である。そうでなければ帰納法の仮定より二つの小配列は正しくソートされる。命題 1.1 より、その小配列を $\textsc{Merge}$ 関数に入力したときの出力はソートされた全体の配列だから、$\textsc{MergeSort}$ は確かに元の配列をソートする。 $\Box$

解析

$\textsc{MergeSort}$ アルゴリズムは再帰的なので、その実行時間は再帰方程式で表されます。 $\textsc{Merge}$ は決まった処理を要素ごとに行う for ループなので、実行時間は $O(n)$ です。よって $\textsc{MergeSort}$ の実行時間 $T(n)$ について次の再帰方程式を得ます: \[ T(n) = T(\lceil n/2 \rceil) + T (\lfloor n/2 \rfloor) + O(n) \]

分割統治法を使ったときに生じるほとんどの再帰方程式と同様に、この式に出てくる床関数と天井関数は無視できます (この章の最後で説明される定義域変換というテクニックを使います)。よって $T(n) =$ $2T(n/2) + O(n)$ です。"全ての段階で等しい" 場合の再帰木の方法 (同じくこの章で説明されます) を使うと $\pmb{T(n) = O(n \log n)}$ という閉じた答えがすぐに分かります。再帰木について (まだ) 知らなかったとしても、 $T(n) = O(n \log n)$ という答えは帰納法で確認できます。

クイックソート

クイックソート (quicksort) もまた再帰的なソートアルゴリズムです。Tony Hoare (トニー・ホーア) によって 1959 年に発見され、1961 年に発表されました。このアルゴリズムの各ステップを次に示します。クイックソートにおいて本当の作業と呼べるのは再帰呼び出しの前に配列を小配列に振り分ける部分であり、この振り分けによって最後のマージ処理が必要なくなります。

配列からピボット (pivot) を選ぶ。
配列を三つの小配列に分ける。三つの配列にはそれぞれピボットよりも小さい要素、ピボットと等しい要素、ピボットよりも大きい要素を入れる。
一番目と三番目の小配列を再帰的にクイックソートする。

\[ \begin{array}{rc} \text{\small 入力}: & \texttt{ S O R T I N G E X A M P L} \\ \text{\small ピボットの選択}: & \texttt{ S O R T I N G E X A M }{\color{#B52F1B}{\texttt{P}}}\texttt{ L} \\ \text{\small 分割}: & \texttt{ A G O E I N L M }{\color{#B52F1B}{\texttt{P}}}\texttt{ T X S R} \\ \text{\small 左の再帰}: & \texttt{ A E G I L M N O }{\color{#B52F1B}{\texttt{P}}}\texttt{ T X S R} \\ \text{\small 右の再帰}: & \texttt{ A E G I L M N O }{\color{#B52F1B}{\texttt{P}}}\texttt{ R S T X} \end{array} \]

図 1.7

クイックソートの例

クイックソートの詳細な手順を次の疑似コードに示します。$\textsc{Partition}$ サブルーチンの入力 $p$ はソートされてない配列におけるピボット要素の添え字であり、出力はピボットの新しい添え字です。効率良く配列を分割するアルゴリズムはいくつか知られていますが、ここに示したのは Nico Lomuto によるものです⁷。変数 $l$ がピボットよりも小さい要素の数を保持します。

procedure $\texttt{QuickSort}$($A[1..n]$)

if $ n > 1 $ then

ピボット $A[p]$ を選ぶ

$ r \leftarrow $$\texttt{Partition}$($A, p$)

$\texttt{QuickSort}$($ A[1..r-1 $]) $\quad$ ⟨⟨再帰！⟩⟩

$\texttt{QuickSort}$($ A[r+1..n $]) $\quad$ ⟨⟨再帰！⟩⟩

procedure $\texttt{Partition}$($A[1..n], p$)

swap $ A[p] \leftrightarrow A[n] $

⟨⟨$l = $ ピボット未満の要素の数⟩⟩

$ l \leftarrow 0 $

for $ i \leftarrow 1 $ to $ n - 1 $ do

if $ A[i] < A[n] $ then

$l \leftarrow l + 1$

swap $ A[l] \leftrightarrow A[i] $

swap $ A[n] \leftrightarrow A[l + 1] $

return $ l + 1 $

図 1.8

クイックソート

正しさ

マージソートと同じように、$\textsc{QuickSort}$ の正しさの証明には帰納法を二回使います。最初に $\textsc{Partition}$ が正しく配列を分割することを示し、次に $\textsc{Partition}$ が正しいという仮定の下で $\textsc{QuickSort}$ が正しいことを示します。 $\textsc{Partition}$ の正しさの証明では次のループ不変条件を示す必要があります: 「メインループの各反復の終端において、小配列 $A[1..l]$ の要素は $A[n]$ よりも小さく、また小配列 $A[l+1..i]$ の要素は $A[n]$ よりも小さくない」簡単なものの面倒なこの証明の詳細は読者への練習問題とします。

解析

クイックソートの解析はマージソートのものと似ています。$\textsc{Partition}$ は決まった処理を要素ごとに行う for ループなので、実行時間は $O(n)$ です。一方 $\textsc{QuickSort}$ の実行時間 $T(n)$ についての再帰的関係はソートした配列におけるピボット要素の順位 $r$ に依存します: \[ T(n) = T(r - 1) + T(n - r) + O(n) \]

もしなんらかのマジカルな方法で配列の $A$ の中央値をピボットとして選択できるなら $r = \lceil n/2 \rceil$ となります。このとき二つの小問題のサイズは可能な範囲で最も近くなり、再帰方程式は次のようになります: \[ T(n) = T(\lceil n/2 \rceil - 1) + T(\lceil n/2 \rceil) + O(n) \leq 2T(n/2) + O(n) \] 再帰木の方法、あるいは「あ、この再帰方程式ってマージソートで解いたじゃん」によって $T(n) = O(n \log n)$ が分かります。

この章でこれから見ることですが、ソートされる前の配列から中央値を選択する処理は実際に線形時間で行えます。しかしアルゴリズムは複雑であり、$O(\cdot)$ という表記に隠されている定数部分が大きすぎるので、このアルゴリズムを使ってソートを実装すると実用できる速さになりません。そのため多くのプログラマーはもっと単純な、例えば配列の最初または最後を選択するといった方法でピボットを選んでいます。この場合 $r$ は $1$ から $n$ の任意の値を取るので、再帰方程式は次のようになります: \[ T(n) = \max_{1 \leq r \leq n} (T(r - 1) + T(n - r) + O(n)) \] 最悪の場合 ―― $r = 1$ または $r = n$ ―― では、二つの小問題の大きさが大きく異なることになり、$T(n) \leq T(n - 1) + O(n)$ となります。この場合の解は $\pmb{T(n) = O(n^{2})}$ です。

ピボットの選択に使われるもう一つのヒューリスティックは "三つの中央値" と呼ばれるものです。これは配列から要素を三つ (よくあるのは配列の最初、中央、最後から) 取り、その中央値をピボットとして採用するという方法です。ピボットを決め打ちで採用するものと比べた場合、この方法を使うと実際の実行速度がいくらか向上します。特に配列が最初から (ほぼ) ソートされている場合では速度の向上が顕著です。しかし最悪の場合では $r = 2$ または $r = n - 1$ となるので、"三つの中央値" ヒューリスティックを使った場合の再帰方程式は $T(n) \leq T(1) + T(n - 2) + O(n)$ であり、この解は $T(n) = O(n^{2})$ のままです。

ピボット要素が "平均して" 配列の中央部分、例えば上から $n/10$ と $9n/10$ の間に収まるはずだというのは直感的に分かります。この直感を信じれば、このアルゴリズムの平均実行時間は $O(n \log n)$ となります。確かにこの直感を定式化することもできますが、最もよく使われる定式化では、入力データの任意の置換が全て同じ頻度で入力されるという、全く現実的でない仮定が置かれます。現実のデータはランダムかもしれませんが、事前にランダムであることが分かるという意味のランダムではありませんし、一様乱数では決してありません⁸！

どういうわけか "最良" 実行時間なるものを考える人もいますが、私たちはしません。

パターン

マージソートとクイックソートで見てきた三段階のパターンは分割統治 (devide-and-conquer)と呼ばれます:

与えられた問題のインスタンスを同じ問題の独立したより小さいインスタンスに分割する (devide)。
小さいインスタンスを再帰の妖精に任せる (delegate)。
小さいインスタンスの答えを元のインスタンスの答えになるよう組み合わせる (combine)。

インスタンスのサイズがある定数よりも小さくなったら、再帰的な処理をやめ、問題を直接解きます。問題を直接解くのは総当たりで、定数時間で行われます。

分割統治法のアルゴリズムが正しいことを示すときにはほとんど常に帰納法が使われます。また実行時間の解析には再帰方程式を解く必要がありますが、再帰木を使えば通常は解くことができます (残念ながらいつも解けるとは限りませんが！)。

再帰木

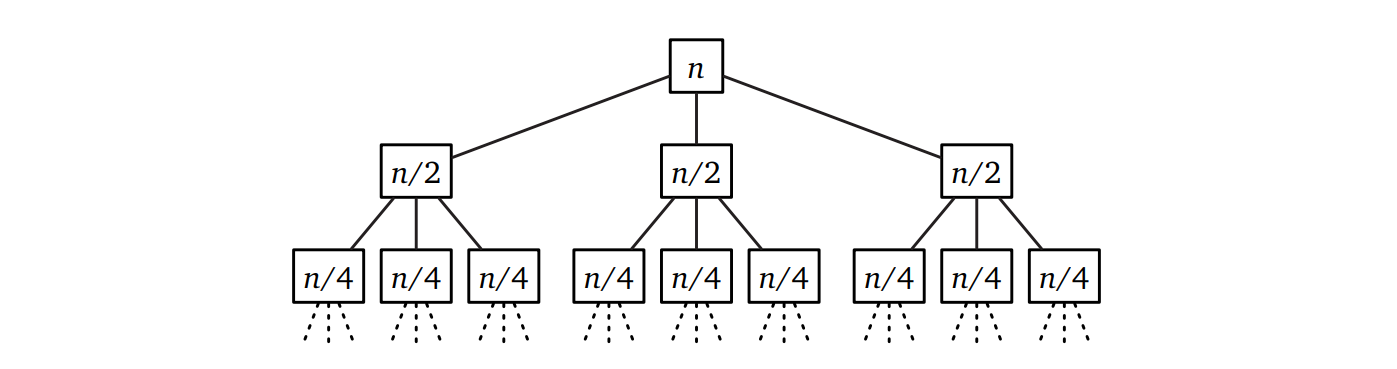
先ほどから何度も出てきている再帰木 (recursion tree) を説明しましょう。再帰木とは分割統治法で出てくる再帰方程式を解くためのツールであり、単純で、多くの問題に適用でき、視覚的に理解が簡単です。

再帰木では根につながっている頂点が再帰的な小問題を表します。頂点の値 (value) とは、その頂点が表す小問題を解くのにかかる時間から再帰呼び出しの分の時間を除いたものです。この定義から、アルゴリズムの実行時間は木に含まれる全ての頂点の値の和であることが分かります。

この考えをもっと理解するために、再帰呼び出し以外の処理に $O(f(n))$ だけ時間がかかるような分割統治法のアルゴリズムを考えます。$r$ 回の再帰呼び出しが行われ、再帰呼び出しのたびに問題のサイズが $\frac{n}{c}$ になると仮定します。このとき $O()$ 記法によって隠れる定数倍を無視すれば、アルゴリズムの実行時間 $T(n)$ は次の再帰方程式に支配されます: \[ T(n) = rT(n/c) + f(n) \]

$T(n)$ に対する再帰木の根の値は $f(n)$ であり、根は $r$ 個の子を持ちます。根の子は全てが $T(n/c)$ に対する再帰木です。全ての頂点は根と同様に $r$ 個の子を持ち、深さ $d$ の頂点は値 $f(n/c^{d})$ を持ちます ($n/c^{d}$ を整数にするために $n$ が $c$ を何乗かしたものと仮定しても構いませんが、こう仮定しなくても結果は変わりません)。

実際に問題を解くときには、最初の二つか三つの木を書いた次のような図を描くとよいでしょう:

図 1.9

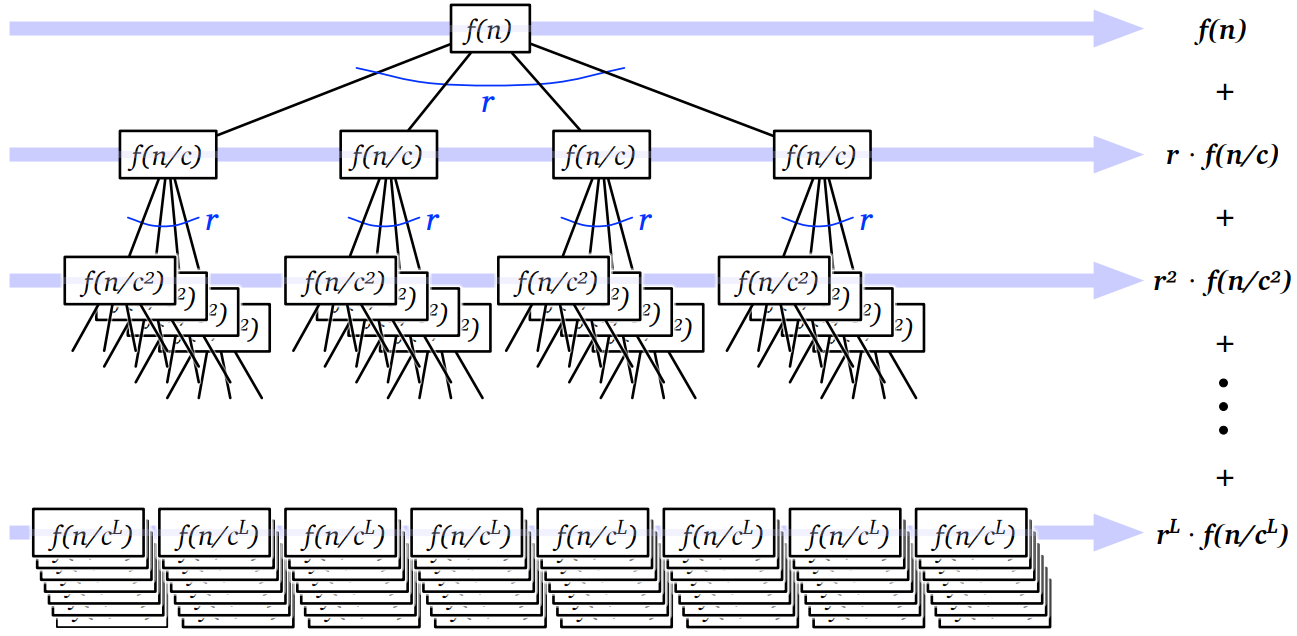
再帰方程式 $T(n) = rT(n/c) + f(n)$ に対する再帰木

再帰木の葉は再帰方程式のベースケースに対応します。今は漸近表記にだけ注目しておりベースケースの正確な値は重要ではないので、全ての $n \leq n_{0}$ について $T(n) = 1$ と仮定しても問題ありません。ここで $n_{0}$ は適当な正の整数定数であり、再帰木を解析するのに便利な値にするのがよいでしょう。ここでは $n_{0} = 1$ としました。

$T(n)$ は木に含まれる全ての値の和です。高さごとに和を求めることでこの和を計算します。整数 $i$ に対して、高さ $i$ の頂点はちょうど $r^{i}$ 個存在し、全て $f(n/c^{i})$ の値を持ちます。したがって \[ T(n) = \sum_{i=0}^{L} r^{i}f(n/c^{i}) \] となります。ここで $L$ は木の高さです。ベースケースにおいて $n_{0} = 1$ だったので、$n/c^{L} = n_{0} = 1$ より $\pmb{L = \log_{c} n}$ となります。木の葉は $r^{L} = r^{\log_{c} n} = n^{\log_{c} r}$ 個だけあるので、これと $f(1) = O(1)$ から、高さによる和 ($\sum$) の最後の項は $n^{\log_{c} r} \cdot f(1) = O(n^{\log_{c}r})$ となります。

高さごとの級数 $\sum$ が特に簡単に計算できる場合が三つあります:

減少列: 和が減少する幾何級数の場合 (全ての項が一つ前の項と比べて定数倍だけ小さいとき)、$T(n) = O(f(n))$ です。和は再帰木の根の値に支配されます。
定数列: 足される全ての項が等しい場合、明らかに $T(n) =$ $O(f(n) \cdot L) =$ $O(f(n) \log n)$ です (定数 $c$ は漸近表記によって隠されました)。
増加列: 和が増加する幾何級数の場合 (全ての項が一つ前の項と比べて定数倍だけ大きいとき)、 $T(n) = O(n^{\log_{c} r})$ です。この場合、和は再帰木の葉の数によって支配されます。

一番目と三番目のケースでは、幾何級数の一番大きい項だけが生き残り、他の項は $O(\cdot)$ 表記の中に飲み込まれてしまいます。減少する幾何級数のケースでは、 $L$ を計算する必要さえありません。なお漸近上界は再帰が無限だったとしても正しくなります！

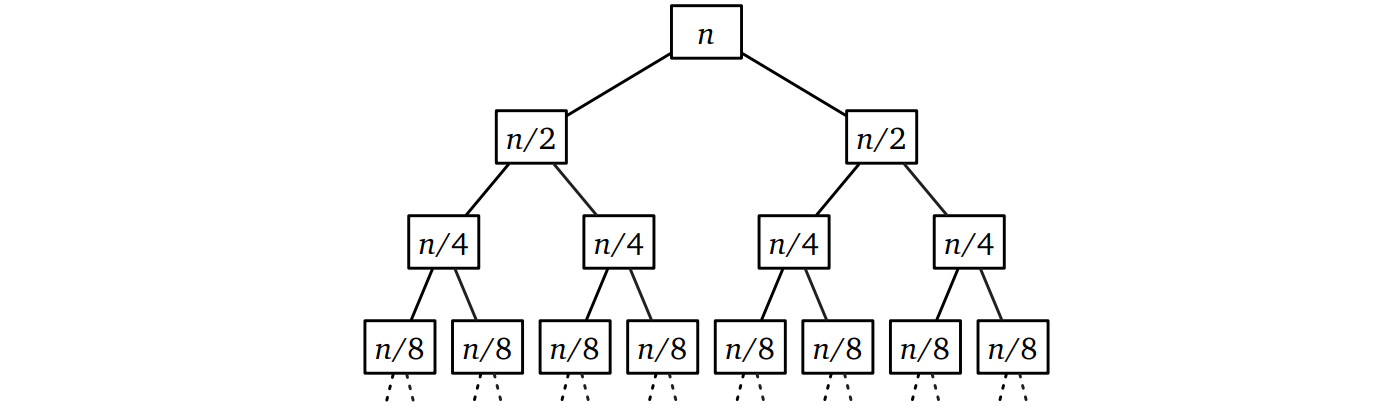
例えばマージソートの (簡略化された) 再帰方程式 $T(n) = 2T(n/2) + O(n)$ について再帰木を書くと、最初のいくつかを書いた時点で同じ高さの頂点の値の和が全て等しいことが分かります (下図)。したがって $T(n) = O(n \log n)$ がすぐに分かります。

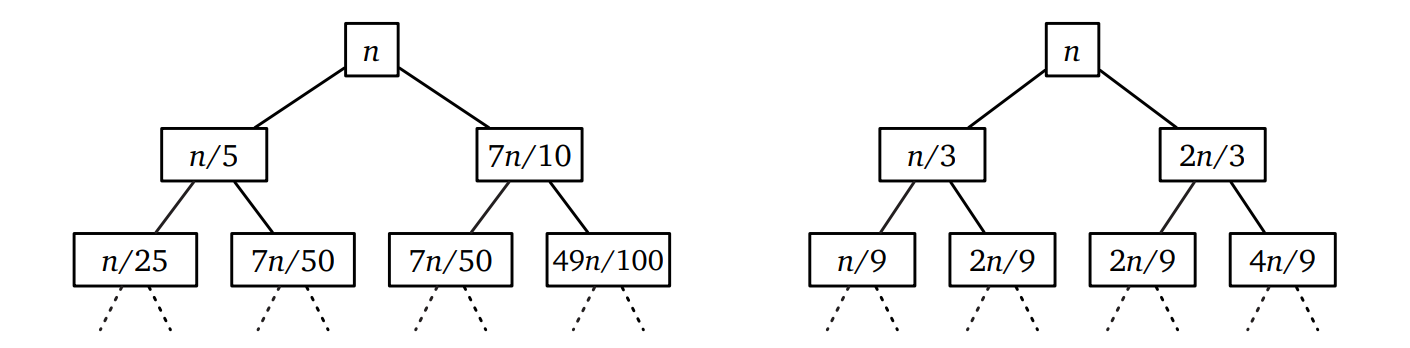
再帰木のテクニックは小問題が異なる大きさを持つアルゴリズムにも適用できます。例えばクイックソートにおいて、何らかの方法でソートされた配列を三分割したときの中央の部分からピボットを必ずに選択できたとします。このとき最悪計算時間が満たす再帰方程式は \[ T(n) \leq T(n/3) + T(2n/3) + O(n) \] を満たします。この式は恐ろしく見えるかもしれませんが、手懐けるのは簡単です。再帰木を何段か書いてみれば、高さごとの値の和が最大でも $n$ である ――木の深い部分ではノードの一部が無くなるので―― ことが分かります。さらに木の高さは $\log_{3/2} n = O(\log n)$ なので、すぐに $T(n) = O(n \log n)$ が分かります (さらに言えば、再帰木に含まれる葉の総数は $\log_{3} n = \Omega (\log n)$ なので、この解析を改善できたとしても定数の範囲でしか改善できません。ただこの改善は私たちの目的には全く関係のないことです)。つまり、再帰木のバランスが取れていなくても関係ありません。

もっと極端な例として、最悪の場合のクイックソートに対する再帰方程式 $T(n) =$ $T(n - 1) + T(1) + O(n)$ を考えると、全くアンバランスな再帰木となります。高さごとの値の和は上述の三つの例のどれにも当てはまりませんが、どの項も $n$ よりも小さく、木の高さが最大 $n$ であることから、$T(n) = O(n^{2})$ が分かります (少なくとも $n/2$ 個の葉が $n/2$ 以上の値を持っているので、ここでもこの保守的な解析が厳密であることが分かります)。

図 1.11

クイックソートの再帰木: ピボットが良い場合 (左) と最悪の場合 (右)

❤ 床関数と天井関数は無視してよい

注意深い読者はここまでのアルゴリズムの解析が重要な部分を無視していると思うかもしれません。というのもマージソートの実行時間は再帰方程式 $T(n) = 2T(n/2) + O(n)$ に厳密には従わないのです。実際のプログラムでは入力サイズは奇数になるので、このように $T(n)$ を表した場合、長さが $42 \frac{1}{2}$ あるいは $17 \frac{7}{8}$ の配列をソートするというような全く無意味な操作に対する時間を求めることになります。マージソートに対する本当の再帰方程式はもっと面倒くさいものでした: \[ T(n) = T(\lceil n/2 \rceil) + T(\lfloor n/2 \rfloor) + O(n) \]

もちろん帰納法を使えばこの再帰方程式でも $T(n) = O(n \log n)$ であることは確かめられますが、うんざりするような計算が必要になります。しかし嬉しいことに、次に示す定義域変換 (domain transformation)という単純なテクニックを使うと、床関数と天井関数を再帰方程式から消すことができます⁹。

まず $T(n)$ を上から評価する。上界を考えていることから、上から評価しても問題ない。二つの小問題が等しいとみなすことで床関数を消し、さらに天井関数に関する不等式を使って天井関数を消す。 \[ T(n) \leq 2 T (\lceil n/2 \rceil) + O(n) \leq 2T(n/2 + 1) + O(n) \]
次に新しい関数 $S(n) = T(n + \alpha)$ を定義する。ここで $\alpha$ は単純にした形の再帰方程式 $S(n) \leq 2 S(n/2) + O(n)$ が満たされるように選ぶ。$\alpha$ の値は $T$ の再帰方程式を使うことで求めることができる: \[ \begin{aligned} S(n) & = T(n + \alpha) && [S \text{ の定義}] \\ & \leq 2 T(n/2 + \alpha / 2 + 1) + O(n) + \alpha && [T \text{ の再帰方程式}] \\ & = 2 S(n/2 - \alpha / 2 + 1) + O(n) + \alpha && [S \text{ の定義}] \end{aligned} \] よってこの例では $\alpha = 2$ とすれば $S(n) \leq 2 S(n/2) + O(n) + 2$ となり、求めていた形となる。
最後に、再帰木の方法によって $S(n) = O(n \log n)$ が分かるので、 \[ T(n) = S(n - 2) = O((n-2)\log(n-2)) = O(n \log n) \] となって証明したい式が得られた。

同様の定義域変換は床関数、天井関数、そして次数の小さい項を任意の分割統治法の再帰方程式から消すのに使えます。今こうして説明したので、これ以降は詳細を省略しましょう！これから分割統治法の再帰方程式では、床関数と天井関数、そして次数の小さい項をそうと示さずに消すことにします。あなたにもそうすることを勧めます。

❤ 線形選択

クイックソートに関する議論の中で、ソートされていない配列から中央値を見つける処理が線形時間で行えると説明しました。この操作のためのアルゴリズムは 1970 年代に Manuel Blum (マヌエル・ブラム)、Bob Floyd (ボブ・フロイド)、Vaughan Pratt (ヴォーン・プラット)、Ron Rivest (ロン・リベスト)、Robert Tarjan (ロバート・タージャン) によって発見されました。彼らのアルゴリズムが扱ったのは $n$ 要素の配列と整数 $k$ を受け取って配列から $k$ 番目に小さい要素を取り出すというもっと一般的な問題であり、この問題を解くアルゴリズムはクイックセレクト (quickselect)あるいは片腕のクイックソート (one-armed quicksort) と呼ばれます。クイックセレクトは Tony Hoare (トニー・ホーア) によって 1961 年に最初に発表されましたが、それは彼がクイックソートを発表した論文のクイックソートを説明したまさにそのページでのことでした。

クイックセレクト

一般的なクイックセレクトアルゴリズムはまずクイックソートと同じようにピボットを選び、$\textsc{Partition}$ サブルーチンを使って配列を分割します。そして二つの配列のうち元の配列で $k$ 番目に小さい要素を含む片方だけに対して再帰呼び出しを行います。疑似コードを次に示します。

procedure $\texttt{QuickSelect}$($ A[1..n], k $)

if $ n = 1 $ then

return $ A[1] $

else

ピボット $A[p]$ を選ぶ

$ r \leftarrow $$\texttt{Partition}$($ A[1..n], p $)

if $ k < r $ then

return $\texttt{QuickSelect}$($ A[1..r-1], k $)

else if $ k > r $ then

return $\texttt{QuickSelect}$($ A[r+1..n], k - r $)

else

return $ A[r] $

図 1.12

クイックセレクト、またの名を片腕のクイックソート

このアルゴリズムには注目すべき特徴が二つあります。一つはクイックソートと同じようにアルゴリズムの正しさがピボットの選択に依存していない点。もう一つは中央値 ($k = n/2$ のケース) だけを考えているにもかかわらず、この Hoare の再帰的な戦略はそれよりも一般的な問題を考えている点です: 入力配列 $A[1..n]$ の中央値が小配列 $A[1..r-1]$ あるいは $A[r+1..n]$ の中央値と等しくなることはまずありません。

$\textsc{QuickSelect}$ の最悪実行時間 $T(n)$ は $\textsc{QuickSort}$ と似た再帰方程式に従います。$r$ が分からないとどちらの配列を再帰的に探索するかが分からないので、最悪の場合を調べなければなりません: \[ T(n) \leq \max_{1 \leq r \leq n} \left\lbrace T(r-1), T(n-r)\right\rbrace + O(n) \] 再帰的に解く問題の大きさを $l$ と置けば、方程式を単純化できます: \[ T(n) \leq \max_{0 \leq l \leq n-1} T(l) + O(n) \]

選択されるピボットが常に配列の中で一番大きい (または一番小さい) 物であった場合、この再帰方程式は $T(n) = T(n - 1) + O(n)$ であり、$T(n) = O(n^{2})$ となります (再帰木は単純な路です)。

良いピボット

もし何らかのマジカルな方法で良いピボットを選ぶことができたなら、二次関数的な最悪ケースを回避できるはずです。ここで言う良いピボットとは、ある $\alpha < 1$ を用いて $l \leq \alpha n$ と書けるピボットです。この場合、再帰方程式は以下のように単純になります: \[ T(n) \leq T(\alpha n) + O(n) \] この方程式は幾何級数に展開されます。その級数は一番大きな項に支配されるので、$T(n) = O(n)$ です (ここでも再帰木は単純な路です。実行時間 $O(n)$ における定数部分は $\alpha$ に依存します)。

言い換えると、中央値に近い値を線形時間で見つけることができるならば、本当の中央値も線形時間で特定できるということです。ここで必要になるのは中央値近似の妖精 (Approximate Median Fairy) です。 Blum-Floyd-Pratt-Rivest-Tarjan アルゴリズムは入力の配列の部分配列を注意深く選び、さらにその部分配列の中央値を選ぶことで、クイックセレクトの良いピボットを再帰的に計算します。中央近似値の妖精とは再帰の妖精が変装した姿だったのです！

詳しく見ていくと、このアルゴリズムはまず入力の配列を $\lceil n/5 \rceil$ 個のブロックに分割します。各ブロックはちょうど 5 個の要素を持ちます(最後の要素は 5 個よりも少ないかもしれませんが、正の無限大を追加することで 5 個にします)。次に各ブロックの中央値を総当たりで求め、それらを新しい配列 $M[1..\lceil n/5 \rceil]$ とします。そしてこの新しい配列の中央値を再帰的に計算します。最後にこの中央値たちの中央値 (median of medians, 疑似コードでは $\mathit{mom}$) をピボットとして片腕のクイックソートを行います。

procedure $\texttt{MomSelect}$($ A[1..n], k $)

if $ n \leq 25 \ $ ⟨⟨または他の適当な数字⟩⟩ then

総当たりで中央値を求める

else

$ m \leftarrow \lceil n / 5 \rceil $

for $ i \leftarrow 1 $ to $m$ do

$ M[i] \leftarrow $$\texttt{MedianOfFive}$($A[5i-4..5i]$) $\quad \hphantom{\ \ }$ ⟨⟨総当たり！⟩⟩

$ \mathit{mom} \leftarrow $$\texttt{MomSelect}$($ M[1..m], \lfloor m/2 \rfloor $) $\quad \hphantom{{}-r}$ ⟨⟨再帰！⟩⟩

$ r \leftarrow $$\texttt{Partition}$($ A[1..n], \mathit{mom} $)

if $k < r$ then

return $\texttt{MomSelect}$($ A[1..r-1], k $) $\quad \hphantom{{}-r}$ ⟨⟨再帰！⟩⟩

else if $k > r$ then

return $\texttt{MomSelect}$($ A[r+1..n], k-r $) $\quad$ ⟨⟨再帰！⟩⟩

else

return $ \mathit{mom} $

$\textsc{MomSelect}$ は再帰を二度使っており、それぞれで計算される値が異なります。最初の再帰ではピボット要素 $\mathit{mom}$ が計算され、次の再帰ではそのピボットを使って小配列の一方から中央値が計算されます。

解析

なぜこのアルゴリズムは高速なのでしょうか？鍵となるのは、中央値たちの中央値が良いピボットであるという事実です。$\mathit{mom}$ は $\lfloor n/5 \rfloor$ 個あるブロックごとの中央値たちの $\lfloor \lceil n/5 \rceil / 2\rfloor - 1 \approx n / 10$ 個よりも大きく、そして各ブロックの中央値はそのブロックの中の二つの要素よりも大きいので、$\mathit{mom}$ は入力の配列の少なくとも $3n / 10$ 要素よりも大きくなります。同様に $3n/10$ 要素よりも小さいことも言えます。したがって、二回目の再帰呼び出しは最大でも配列の $7n/10$ しか探索しません。

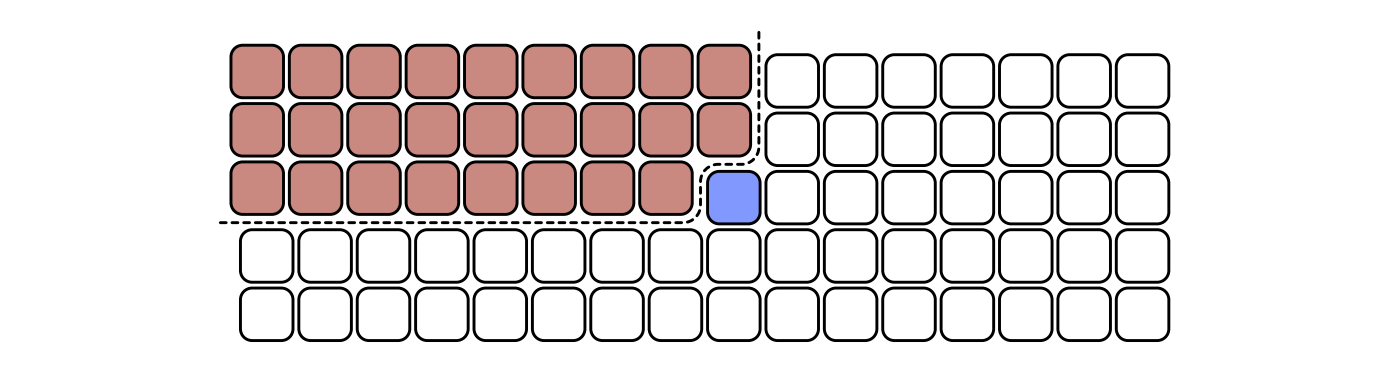
入力の配列を $5 \times \lceil n/5 \rceil$ の格子に描くとこのアルゴリズムの振る舞いが分かりやすくなります。ここで各列は五つの連続する要素からなるブロックです。図を分かりやすくするために、列の要素を上から下にソートし、さらに列ごとの中央値で列をソートしておきます (アルゴリズムではこの二番目のソートをしないことに注意してください)。こうした場合、中央値たちの中央値は格子の中心に一番近い要素となります。

格子の左上の要素が $\mathit{mom}$ よりも小さい $3n / 10$ 個の要素を示します。探索している要素が $\mathit{mom}$ よりも大きい場合、この $3n/10$ 個の要素は以降の探索から除外されます。そのため再帰的な小問題の入力サイズは最大でも $7n/10$ となります。同様に探索している要素が $\mathit{mom}$ よりも小さい場合には $\mathit{mom}$ よりも大きい $3n/10$ 個の要素が探索から除外されます。つまり再帰的に解く小問題のサイズは必ず $7n / 10$ 以下です。

これで $\mathit{mom}$ が良いピボットであることはわかりました。しかしこのアルゴリズムは二つの再帰呼び出しをしています。どうすればこれが線形時間だと証明できるでしょうか？ここで鍵となるのは、再帰的に解く二つの小問題のサイズの和が入力のサイズよりも定数倍で小さいという事実です。このアルゴリズムの最悪計算時間は次の再帰方程式を満たします: \[ T(n) \leq T(n/5) + T(7n/10) + O(n) \]

この再帰方程式に対応する再帰木を描くと、高さごとの値の和が一つ上の値の和の $ 9 / 10 $ 以下であることが分かります。したがって高さごとの値の和の合計は減少幾何級数であり、解は $T(n) = O(n)$ です (ここでも再帰木のバランスが取れていませんが、何の問題もありません)。やったぜ！ Thanks, Mom!

図 1.13

$\textsc{MomSelect}$ に対する再帰木 (左) とブロックの大きさを 3 としたときの再帰木 (右)

サニティチェック

ここまでくると、多くの生徒がマジックナンバー 5 について質問をしてきます。なぜこの数字を選んだのですか、と。その質問に対する答えは「実行時間を表す和が減少幾何級数となる最小の奇数が 5 だから」です (ブロックのサイズを偶数にすると手続きが複雑になります)。仮にブロックのサイズを 3 とすると、実行時間が満たす再帰方程式は次のようになります: \[ T(n) \leq T(n/3) + T(2n/3) + O(n) \] この再帰方程式には見覚えがあります！この場合、再帰木の高さごとの値の和は常に $n$ 以下です。再帰木の葉の高さは同じではありませんが、上界を求めるために一番深い葉の高さ $ \log_{3 / 2} n $ を考えると、再帰木全体の値は最大 $ n \log_{3 / 2} n = O(n \log n) $ です。したがって再帰方程式の解として $T(n) \leq O(n \log n)$ が得られます。一方で一番浅い葉の高さは $\log_{3} n$ なので、この上界を定数倍以上に改善することはできません。よって三分割による中央値の中央値選択はソートと同じ速さとなってしまいます。

アルゴリズムをさらに詳細に解析すると、比較演算だけを考えたとしても $O()$ 表記で隠される定数部分が非常に大きいということが分かります。5 要素の配列の中央値を求めるには比較が最大 6 回必要となるので、再帰的な小問題を組み立てるのには最大 $ 6n / 5$ 回の比較が必要になります。その再帰呼び出しの後の分割処理はナイーブに実装すれば $n - 1$ 回の比較が必要になります。ただし分割を行う時点で配列の要素のうち $ 3n / 10$ 個はピボットとの大小が分かっているので、追加で必要となる比較は $2n / 5$ 回となります。したがって、最悪ケースの比較演算の回数に関する再帰方程式は次のようになります: \[ T(n) \leq T(n / 5) + T(7n / 10) + 8n / 5 \] 再帰木の方法を使うと、上界が求まります: \[ T(n) \leq \frac{8n}{5} \sum_{i \geq 0} \left(\frac{9}{10}\right)^{i} = \frac{8n}{5} \cdot 10 = 16n \] 実際に中央値の中央値アルゴリズムを動かすとこの最悪ケースほどはひどくなりません ――全ての再帰呼び出しで最悪ケースを引く確率はとても低いからです―― が、常識的に十分大きいとみなされるような配列においてさえ、ソートよりも遅くなることがあります¹⁰。

高速乗算

前章では、$n$ 桁の数の乗算を $O(n^{2})$ で行う古くからあるアルゴリズムをいくつか紹介しました。小学校で習う格子アルゴリズムや、エジプト人農民の乗算アルゴリズムです。

桁ごとの数を収めた配列を分割して、さらに次の等式を使えばもっと効率の良いアルゴリズムが作れそうです: \[ (10^{m}a + b)(10^{m}c + d) = 10^{2m}ac + 10^{m}(bc + ad) + bd \] この再帰方程式から以下に示す分割統治法を使ったアルゴリズムが作れます。$n$ 桁の整数 $x$ と $y$ の積を計算するアルゴリズムであり、$ac, bd, ad, bd$ という部分積を再帰的に計算しています。最後の行の乗算は再帰的になっていませんが、$10$ を掛ける処理は桁をひとつずらすことに対応するので、$O(n)$ 時間で行えます。

procedure $\texttt{SplitMultiply}$($ x,y,n $)

if $ n = 1 $ then

return $ x \cdot y $

else

$ m \leftarrow \lceil n / 2 \rceil $

$ a \leftarrow \lfloor x / 10^{m} \rfloor;\ b \leftarrow x \text{ mod } 10^{m}$ $\quad$ ⟨⟨$x = 10^{a} + b$⟩⟩

$ c \leftarrow \lfloor x / 10^{m} \rfloor;\ d \leftarrow x \text{ mod } 10^{m}$ $\quad$ ⟨⟨$y = 10^{c} + d$⟩⟩

$ e \leftarrow $$\texttt{SplitMultiply}$($ a,c,m $)

$ f \leftarrow $$\texttt{SplitMultiply}$($ b,d,m $)

$ g \leftarrow $$\texttt{SplitMultiply}$($ b,c,m $)

$ h \leftarrow $$\texttt{SplitMultiply}$($ a,d,m $)

return $ 10^{2m} e + 10^{m}(g + h) + f $

このアルゴリズムの正しさは帰納法で簡単に証明できます。実行時間は次の再帰方程式を満たします: \[ T(n) = 4T(\lceil n/2 \rceil) + O(n) \]

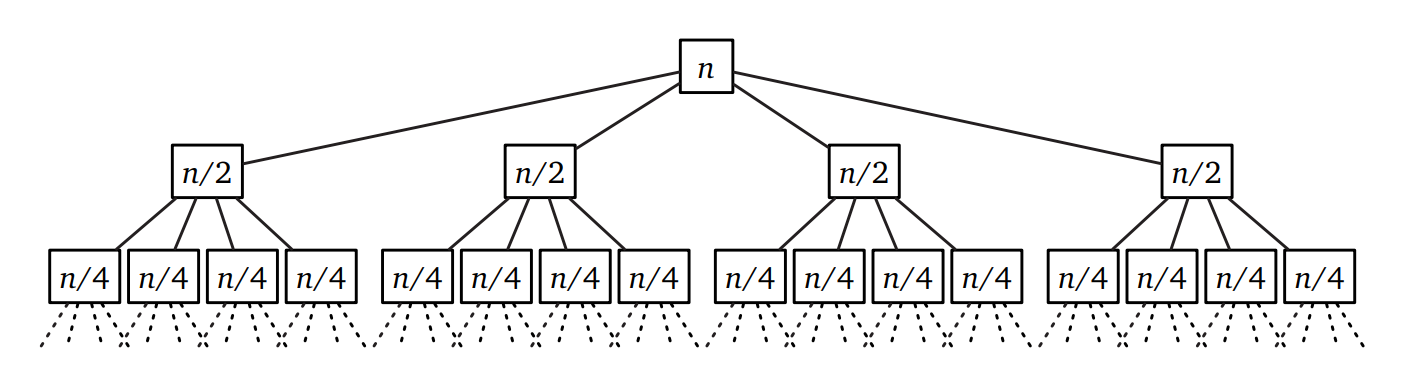
再帰木の方法を使うと、再帰方程式は増加幾何級数となることが分かります。つまり $T(n) =$ $O(n^{\log_{2} 4}) =$ $O(n^{2})$ です。結局、このアルゴリズムは格子アルゴリズムと同じように $x$ と $y$ の各桁をかけているだけなのです。だからこのアルゴリズムでは高速化できません。残念、うまくいくと思ったんですが。

二十世紀を代表する数学の巨人の一人である Andrei Kolmogorov (アンドレイ・コルモゴロフ) は 1950 年代の中頃、 $n$ 桁の乗算を $o(n^{2})$ で行うアルゴリズムは存在しないという予想を発表しました。1960 年、Kolmogorov はモスクワ大学で開かれたセミナーで自身の "$n^{2}$ 予想" を再表明し、これに関連する問題をこれからの議題として提案しました。それからちょうど一週間後、Anatolii Karatsuba (アナトリー・カラツバ) という 23 才の学生が Kolmogorov のもとを訪れ、注目すべき反例を示しました。Karatsuba 本人によると:

セミナーが終わってから、$n^{2}$ 予想を否定的に解決する新しいアルゴリズムについて Kolmogorov に伝えた。成り立つはずだと思っていた予想と矛盾するアルゴリズムを見て、Kolmogorov はとても当惑したようだった。次のセミナーの場で Kolmogorov は私のアルゴリズムを自分で参加者に説明し、セミナーはそこで終了となった。

Karatsuba が気付いたのは、中央の $bc + ad$ という係数が他の係数 $ac$ と $bd$ から計算でき、そのときに再帰的な掛け算が一度しか必要にならないということでした。つまり、次の代数的等式です: \[ ac + bd - (a - b)(c - d) = bc + ad \] このトリックを使って上述のアルゴリズムを書き換えると、再帰的な呼び出しが三回で済みます:

procedure $\texttt{FastMultiply}$($ x,y,n $)

if $ n = 1 $ then

return $ x \cdot y $

else

$ m \leftarrow \lceil n / 2 \rceil $

$ a \leftarrow \lfloor x / 10^{m} \rfloor;\ b \leftarrow x \text{ mod } 10^{m}$ $\quad$ ⟨⟨$x = 10^{a} + b$⟩⟩

$ c \leftarrow \lfloor x / 10^{m} \rfloor;\ d \leftarrow x \text{ mod } 10^{m}$ $\quad$ ⟨⟨$y = 10^{c} + d$⟩⟩

$ e \leftarrow $$\texttt{FastMultiply}$($ a,c,m $)

$ f \leftarrow $$\texttt{FastMultiply}$($ b,d,m $)

$ g \leftarrow $$\texttt{FastMultiply}$($ a-b,c-d,m $)

return $ 10^{2m} e + 10^{m}(e + f - g) + f $

Karatsuba のアルゴリズム $\textsc{FastMultiply}$ の実行時間が従う再帰方程式は以下です: \[ T(n) \leq 3 T(\lceil n/2 \rceil) + O(n) \] ここでも、再帰的な議論においては天井関数を無視しても構いません。再帰木の方法を使うと再帰方程式は増加幾何級数となりますが、この場合の解は $T(n) = $ $O(n^{\lg 3}) = $ $\pmb{O(n^{1.58496})}$ であり、二次関数だった以前のアルゴリズムから驚くべき高速化です¹¹。Karatsuba のアルゴリズムがアルゴリズムの設計と解析という行為を正式な研究の対象にしたと言っても過言ではありません。

Karatsuba のアイデアを推し進めて数をさらに複雑に切り分けると、さらに高速な乗算アルゴリズムを得ることができます。Andrei Toom (アンドレイ・トゥーム) は、任意の整数を $k$ 個の部分に分け、これら $n/k$ 桁の部分の間の再帰的な乗算を $2k - 1$ 回だけ使って元の積を計算するというアルゴリズムの無限クラスを発見しました。Stephen Cook (スティーブン・クック) は自身の博士論文において Toom のアルゴリズムの単純にしたものを示しています。任意の固定された $k$ について、Toom-Cook のアルゴリズムの実行時間は $O(n^{1 + 1/(\lg k)})$ です。ここで $O(\cdot)$ に隠れている定数部分は $k$ に依存します。

Carl Friedrich Gauss (カール・フリードリヒ・ガウス) による高速フーリエ変換 (fast fourier transform)¹² の発見も、元をたどればこの分割統治による戦略を使っていると言えます。基本的なFFT アルゴリズムの実行時間は $O(n \log n)$ であり、 FFT を整数の乗算に使うと多少のオーバーヘッドが生じます。FFT を使った最初の整数乗算アルゴリズムは Arnold Schönhage (アーノルド・ショーンハーゲ) と Volker Strassen (フォルカー・ストラッセン) によって 1971 年に発表されており、その実行時間は $O(n \log n \log \log n)$ です。Schönhage-Strassen のアルゴリズムはその後数十年に渡って最速の整数乗算アルゴリズムであり続けました。後に技術的な改善が Martin Fürer によって発見され、ついに 2019 年には David Harvey と Joris van der Hoeven が $O(n \log n)$ 時間で整数の積を計算するアルゴリズムを発表しました¹³。

べき乗

与えられた実数 $a$ と正の整数 $n$ について、$a^{n}$ を計算する問題を考えましょう。標準的でナイーブな実装は単純な for ループを使うものです。$n - 1$ 回の $a$ による乗算が行われます:

procedure $\texttt{SlowPower}$($ a,n $)

$ x \leftarrow a $

for $ i \leftarrow 2 $ to $ n $ do

$ x \leftarrow x \cdot a $

return $x$

入力パラメータ $a$ は整数でも、有理数でも、浮動小数点数でも構いません。さらに言えば、乗算の方法さえ分かっていれば数でなくても構いません。例えば同じアルゴリズムを使って底が有限のモジュロ演算 (暗号アルゴリズムでよく使われる演算) や、行列積 (再帰方程式の評価やグラフの最短路の計算に使われる演算) に関するべき乗を計算できます。何を掛けているのかわからないので、乗算の実行時間は分かりません。そのため実行時間の解析は乗算の数を基準にして行います。

このアルゴリズムよりもずっと速い分割統治アルゴリズムがあります。一番古い記録では紀元前二世紀にインド人韻律学者 Piṅgala (ピンガラ) によって発見されているアルゴリズムで、次の単純な再帰的関係を使うものです: \[ \displaystyle a^{n} = \begin{cases} 1 & \text{if } n = 0 \\ (a^{n/2})^{2} & \text{if } n > 0 \text{ かつ } n \text{ が偶数} \\ (a^{\lfloor n/2 \rfloor})^2 \cdot a & \text{それ以外} \\ \end{cases} \]

procedure $\texttt{PiṅgalaPower}$($ a,n $)

if $ n = 1 $ then

return $ a $

else

$ x \leftarrow $$\texttt{PiṅgalaPower}$($ a, \lfloor n/2 \rfloor $)

if $n$ が偶数 then

return $ x \cdot x $

else

return $ x \cdot x \cdot a $

このアルゴリズムにおける乗算演算の回数 $T(n)$ は再帰方程式 $T(n) \leq T(n/2) + 2$ を満たし、再帰木の方法を使えば解 $T(n) = O(\log n)$ が分かります。

ほとんど同一のべき乗アルゴリズムを前章で触れたエジプト人農民の掛け算アルゴリズムから導くこともできます。足し算を掛け算に (つまり duplation を squaring (二乗すること) に) 置き換えれば次のようになります: \[ a^{n} = \begin{cases} 1 & \text{if } n = 0 \\ (a^{2})^{n/2} & \text{if } n > 0 \text{ かつ } n \text{ が偶数} \\ (a^{2})^{\lfloor n/2 \rfloor} \cdot a & \text{それ以外} \\ \end{cases} \]

procedure $\texttt{PeasantPower}$($ a,n $)

if $ n = 1 $ then

return $ a $

else if $n$ が偶数 then

return $\texttt{PeasantPower}$($a^{2}, n/2$)

else

return $\texttt{PeasantPower}$($a^{2}, \lfloor n/2 \rfloor$)$\ \cdot\ a $

このアルゴリズム ――"squareing and mediation" という名前が相応しいかもしれません―― が行う乗算は $O(\log n)$ 回だけです。これら二つのアルゴリズムはどちらも漸近的に最良です。なぜなら指数部分は乗算ごとに最大でも二倍にしかならないので、$a^{n}$ を計算するどんなアルゴリズムも $\Omega(\log n)$ 回の乗算が必要になるからです。

さらに言うと、$n$ が 2 のべきのとき、これらのアルゴリズムは $\log_{2} n$ 回の乗算を行う最良のアルゴリズムそのものになります。しかし他の $n$ の値では少しだけ速い方法が存在します。例えば $\textsc{PiṅgalaPower}$ と $\textsc{PeasantPower}$ は $a^{15}$ を計算するのに乗算を 6 回行いますが、最良の場合 5 回で済ますことができます: \[ \begin{aligned} \textsc{Piṅgala}: & \quad a \rightarrow a^{2} \rightarrow a^{3} \rightarrow a^{6} \rightarrow a^{7} \rightarrow a^{14} \rightarrow a^{15} \\ \textsc{Peasant}: & \quad a \rightarrow a^{2} \rightarrow a^{4} \rightarrow a^{8} \rightarrow a^{12} \rightarrow a^{14} \rightarrow a^{15} \\ \text{最良 }: & \quad a \rightarrow a^{2} \rightarrow a^{3} \rightarrow a^{5} \rightarrow a^{10} \rightarrow a^{15} \end{aligned} \] 任意の $n$ について $n$ 乗を計算するために必要な最小の乗算回数を効率良く計算する問題は長い間未解決です。

練習問題

Hanoi の塔

以下に示す再帰的でないアルゴリズムがそれぞれ上述した再帰的なアルゴリズムと全く同じ操作を行うことを示してください。同じ円盤を、同じ杭から同じ杭に、同じ順番で動かすことを示してください。三つの杭を $0$, $1$, $2$ で表し、$n$ 個の円盤を $0$ から $2$ に移動させるとします (図 1.1 参照)。
1. $n$ が偶数ならば、杭 $1$ と $2$ の名前を交換する。$i$ 番目のステップにおいて、杭 $i \text{ mod } 3$ を使わないで行える唯一の操作を行う。もし行える操作がないならば、全ての円盤が杭 $i \text{ mod } 3$ にあるので、パズルは解けている。
2. 最初の操作として、$n$ が偶数なら円盤 $1$ を杭 $1$ に、$n$ が奇数なら円盤 $1$ を杭 $2$ に移動させる。それ以降は可能な操作のうち直前の操作で使わなかった円盤を使う (唯一の) ものを行う。もし可能な操作が存在しない場合、パズルは解けている。
3. 円盤 $n+1, n+2, n+3$ がそれぞれ杭 $0, 1, 2$ にあるとして、次の条件を満たす操作を可能な限り繰り返す。
  - 奇数の円盤を他の奇数の円盤のすぐ上に置かない。
  - 偶数の円盤を他の偶数の円盤のすぐ上に置かない。
  - 直前の動作を打ち消さない。
4. $\rho(n)$ で $n / 2^{k}$ が整数でないような最小の $k$ を表すことにする。例えば $42 / 2^{1}$ は整数だが $42 / 2^{2}$ は整数でないので $\rho(42) = 2$ である (同値な定義として、$\rho(n)$ を $n$ を二進法表したときの最下位の $1$ の位置に $1$ を足したもの、とすることもできる)。$\rho(n)$ は振る舞いが定規の目盛りに似ているので、定規関数 (ruler function) と呼ばれることがある。この関数を使った以下のアルゴリズム:
  
  procedure $\texttt{RulerHanoi}$($n$)
  
  $ i \leftarrow 1 $
  
  while $ \rho (i) \leq n $ do
  
  if $n - i$ が奇数 then
  
  円盤 $\rho(i)$ を前に動かす $\quad$ ⟨⟨$0 \rightarrow 1 \rightarrow 2 \rightarrow 0$⟩⟩
  
  else
  
  円盤 $\rho(i)$ を後に動かす $\quad$ ⟨⟨$0 \rightarrow 2 \rightarrow 1 \rightarrow 0$⟩⟩
  
  return $i \leftarrow i + 1$
チャイニーズリング、九連環、Chinese linked rings、Baguenaudier、Cardan's Rings (カルダノの輪)、Meleda、Patience、Tiring Irons、Prisoner's Lock、Spin-Out など様々な名前で呼ばれる中国由来のパズルがあり、このパズルは Hanoi の塔パズルの古い先祖とみなすことができます。このパズルは十六世紀には中国とヨーロッパの両方でよく知られており、イタリア人数学者 Luca Pacioli (ルカ・パチョーリ) は未発表の著作 De Viribus Quantitatis でこのパズルの輪が七つのバージョンを解法と共に説明しています¹⁴。この著作が書かれたのは 1498 年から 1506 年の間のことでしたが、それから数年後、明の詩人の楊慎は輪が九つのバージョンを「女子供のためのおもちゃ」と表現しています。出典は不確かですが、一説によるとこのパズルは二世紀に中国の将軍が、自分が戦争に出ている間に妻が時間をつぶせるようにと作らせたのが起源だそうです。

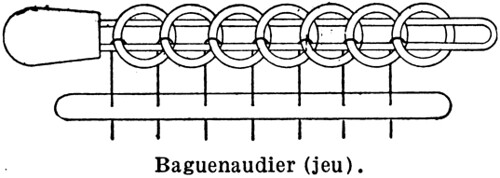図 1.16

カルダノの輪¹⁵

チャイニーズリングにはいろいろな種類がありますが、もっともよく知られているのは長い金属のループといくつかの小さい輪、小さい輪につながった両端が輪になった棒、その棒の反対側につながったベースからなります。ループには上図のように小さな輪が突き刺さっていて、この小さな輪を全て取り除くのがパズルのゴールとなります。

このパズルを次のように抽象化します。各リングの状態を $0$ か $1$ で表し、 $1$ がリングがループに通っていることを、 $0$ がリングがループから離れていることを表します (リングの添え字は出口に近い方が若い番号となります)。このパズルで許されている操作は次の通りです:
- 一番目の (一番出口に近い) ビットはいつでも反転できる。
- パズルの状態を表すビット列がちょうど $z$ 個の $0$ で終わるならば、$z + 2$ 番目のビットを反転できる。
パズルのゴールは $1$ だけの状態から $0$ だけの状態に遷移させることです。例えば、次の 21 回の操作は輪が 5 個のパズルを解きます。 \[ \begin{aligned} \texttt{11111} & \xrightarrow{1} \texttt{11110} \xrightarrow{3} \texttt{11010} \xrightarrow{1} \texttt{11011} \xrightarrow{2} \texttt{11001} \xrightarrow{1} \texttt{11000} \\ & \xrightarrow{5} \texttt{01000} \xrightarrow{1} \texttt{01001} \xrightarrow{2} \texttt{01011} \xrightarrow{1} \texttt{01010} \xrightarrow{3} \texttt{01110} \\ & \xrightarrow{1} \texttt{01111} \xrightarrow{2} \texttt{01101} \xrightarrow{1} \texttt{01100} \xrightarrow{4} \texttt{00100} \xrightarrow{1} \texttt{00101} \\ & \xrightarrow{2} \texttt{00111} \xrightarrow{1} \texttt{00110} \xrightarrow{3} \texttt{00010} \xrightarrow{1} \texttt{00011} \xrightarrow{2} \texttt{00001} \xrightarrow{1} \texttt{00000} \end{aligned} \]
1. ♦ ある操作が直前の動作と同じでないとき、その動作を既約と呼ぶことにします。任意の非負整数 $n$ について、輪が $n$ 個あるチャイニーズリングパズルを解く既約な操作の列はちょうど一つだけ存在することを示してください。[ヒント: グラフを知っている場合、この問題はとても簡単になります。]
2. チャイニーズリングパズルを解くアルゴリズムを説明してください。アルゴリズムの入力は輪の数 $n$ であり、出力はパズルを解く既約な操作の列です。例えば整数 $5$ が入力された場合のアルゴリズムの出力は $1, 3, 1, 2, {}$$1, 5, 1, 2, {}$$1, 3, 1, 2, {}$$1, 4, 1, 2, {}$$1, 3, 1, 2, 1$ です。
3. 前問のアルゴリズムが出力する操作列の長さを $n$ の関数として表してください。その答えが正しいことを証明してください。
Hanoi の塔に関するあまり知られていない話をしましょう。十三世紀、寺院を Benares から Pisa に移築したときのことです。この移築は裕福な商人であり数学者でもあった Leonardo Fibonacci が、神聖ローマ皇帝フリードリヒ 2 世の命を受けて行いました。教皇は十字軍から帰還した兵士たちから寺院について聞いていたのです。この移築によって Pisa の塔とそこに住む僧侶たちは有名になり、イタリア半島において Pisa が交易の中心となるきっかけの一つとなりました。

しかしこの移築が完了して早々、不幸な事件が起こりました。ダイアモンドの棒が傾いてしまったのです。これを受けて Fibonacci は、棒が傾きすぎて使えなくなってしまわないよう円盤を動かすルールを緩めました: 傾いている棒に刺さっている円盤は、他の棒へ一度に移動させても構わないことにしたのです。引き続き大きな円盤を小さな円盤の上に置くのは禁止され、垂直な棒から円盤を動かすときには円盤は一つずつしか移動させることはできません。

図 1.17

Pisa の塔 (五番目の操作で二つの円盤が傾いた棒からまとめて移動されている)

Fibonacci が定めた新しいルールによって、Pisa に移り住んだ司祭たちは Benares にいたときよりもいくらか速く宇宙の終わりを迎えられるようになりました。しかし幸いにも新しく教皇となったグレゴリウス 9 世がフリードリヒ 2 世を破門し、寺院は Pisa から Benares に返還されたので、異国の奇妙な数学的儀式に興味を持つ司祭は減っていきました。それからしばらくして、寺院がかつてあった場所に鐘楼が建てられましたが、この建物は建設されるやいなや傾いてしまったといいます¹⁶。

垂直な棒からもう一つの垂直な棒へ $n$ 個の円盤を最小回数の操作で移動させるアルゴリズムを説明、解析してください。アルゴリズムが実行する操作は正確に何回ですか？
次に示す制限されたHanoi の塔パズルに関する問に答えてください。三つの杭を $0, 1, 2$ で表し、$n$ 個の円盤を $0$ から $2$ に移動させることがゴールです。
1. 杭 $1$ から杭 $2$ に円盤を移動させるのが禁止されているとします。つまり、全ての操作が杭 $0$ を経由しなければならないということです。このバージョンのパズルを最小回数の操作で解くアルゴリズムを説明してください。アルゴリズムが実行する操作は正確に何回ですか？
2. ♣ ❤ 杭 $0$ から杭 $2$、杭 $2$ から杭 $1$、杭 $1$ から杭 $0$ への操作だけが許されているとします。同じ条件を言い換えると、杭が環になっていて、反時計回りの操作だけが許されているということです。このバージョンのパズルを最小回数の操作で解くアルゴリズムを説明してください。アルゴリズムが実行する操作は正確に何回ですか？
  
  図 1.18
  
  反時計回りバージョンの Hanoi の塔問題の、解答の最初の数手
3. ♣ ❤ 最後に、杭 $0$ から杭 $2$ に円盤を動かせないとします。このバージョンのパズルを最小回数の操作で解くアルゴリズムを説明してください。アルゴリズムが実行する操作は正確に何回ですか？ [ヒント: 行列！このバージョンの解析は他の二つよりもはるかに難しいです。]
Hanoi の塔パズルの次の複雑な変種を考えます。$1$ から $k$ と名前の付いた杭が全部で $k$ 個あり、各操作で許されているのは任意の整数 $i$ について杭 $i$ にある一番小さい円盤を杭 $i - 1$ または $i + 1$ に移動させることだけです。通常の Hanoi の塔と同様に円盤はそれよりも小さい円盤の上に乗ることができません。パズルのゴールは $n$ 個の円盤を杭 $1$ から杭 $k$ に移動させることです。
1. $k = 3$ の場合の再帰的アルゴリズムを説明してください。アルゴリズムが実行する操作は正確に何回ですか？ (これは練習問題 1.4.(a) と全く同じ問題です)
2. $k = n + 1$ の場合の再帰的アルゴリズムで、操作が最大でも $O(n^{3})$ 回のものを説明してください。 [ヒント: (a) を使います。]
3. ❤ $k = n + 1$ の場合の再帰的アルゴリズムで、操作が最大でも $O(n^{2})$ 回のものを説明してください。[ヒント: (a) を使いません。]
4. ❤ $k = \sqrt{n}$ の場合の再帰的アルゴリズムで、操作が最大でも多項式回のものを説明してください。 (どんな多項式ですか？)
5. ❤ 任意の $n$ と $k$ に対する再帰的アルゴリズムを説明、解析してください。操作の回数が $n$ の多項式となるためには、$k$ は ($n$ の関数として) どの程度小さくないといけませんか？
${}$
再帰木
再帰木を使って次の再帰方程式を解いてください。 \[ \begin{aligned} A(n) &= 2 A(n/4) + \sqrt{n} & B(n) &= 2 B(n/4) + n & C(n) &= 2 C(n/4) + n^{2} \\ D(n) &= 3 C(n/3) + \sqrt{n} & E(n) &= 3 E(n/3) + n & F(n) &= 3 F(n/3) + n^{2} \\ G(n) &= 4 G(n/2) + \sqrt{n} & H(n) &= 4 H(n/2) + n & I(n) &= 4 I(n/2) + n^{2} \end{aligned} \]
再帰木を使って次の再帰方程式を解いてください。 \[ \begin{aligned} J(n) &= J(n/2) + J(n/3) + J(n/6) + n \\ K(n) &= K(n/2) + 2 K(n/3) + 3 K(n/4) + n^{2} \\ L(n) &= L(n/15) + L(n/10) + 2L(n/6) + \sqrt{n} \end{aligned} \]
❤ 再帰木を使って以下の再帰方程式を解いてください。 \[ \begin{aligned} M(n) &= 2 M(n/2) + O(n \log n) \\ N(n) &= 2 N(n/2) + O(n / \log n) \\ P(n) &= \sqrt{n}P(\sqrt{n}) + n \\ Q(n) &= \sqrt{2n} Q(\sqrt{2n}) + n \end{aligned} \]

${}$

ソート
直径が異なる $n$ 個のパンケーキが積み上がっている様子を想像してください。この状況から上から順に小さいパンケーキが並ぶように並び替えたいとします。ただし許されている動作はフリップ ――1 から $n$ の整数 $k$ について、上から $k$ 番目のパンケーキの下にへらを入れ、それより上にあるパンケーキを全てひっくり返す―― のみです。

図 1.19

4 つのパンケーキをフリップする
1. $n$ 個のパンケーキが任意に積みあがった状態から、$O(n)$ 回のフリップでソートを行うアルゴリズムを説明してください。最悪ケースでは正確に何回のフリップが必要になりますか¹⁷？ [ヒント: この問題はHanoi の塔とは関係がありません。]
2. $n$ を任意の正の整数として、ソートするのに $\Omega(n)$ 回のフリップが必要となる $n$ 個のパンケーキの積み上げ方を示してください。
3. 全てのパンケーキの片側に焼き目がついているとします。任意に積み上げられた $n$ 個のパンケーキを、焼き目がある面が全て下になるようにソートする $O(n)$ 回のフリップを求めるアルゴリズムを説明してください。最悪ケースでは正確に何回のフリップが必要になりますか？
クイックソートのピボット選択における「三つの中央値 (median of three)」ヒューリスティックとは、配列の最初、最後、中央の要素のうち中間のものをピボットとして選ぶというものです。三つの中央値ヒューリスティックが最悪ケースではソートに $\Omega(n^{2})$ 時間かかることを示してください。また任意の整数 $n$ について、三つの中央値クイックソートにおける全ての再帰呼び出しにおいて、ピボットが常に配列の中で二番目に小さい要素となるような 1 から $n$ までの整数の並び替えを示してください。並び替えを考える上では $\textsc{Partition}$ サブルーチンに関する深い知識が必要となります。
1. まずは準備運動として、$\textsc{Partition}$ サブルーチンが安定、つまりピボットよりも小さい要素の順番およびピボットよりも大きい要素の順番を保存するとして問題を解いてください。
2. ❤ $\textsc{Partition}$ が本文中にあるものだとして問題を解いてください。本文中の $\textsc{Partition}$ は安定ではありません。
1. Hey, Moe! Hey, Larry! このアルゴリズムが入力を正しくソートすることを示してくれ！
  
  procedure $\texttt{StoogeSort}$($ A[0..n-1] $)
  
  if $ n = 2 $ かつ $ A[0] > A[1] $ then
  
  swap $ A[0] \leftrightarrow A[1] $
  
  else if $ n > 2 $ then
  
  $ m = \lfloor 2n / 3 \rfloor $
  
  $\texttt{StoogeSort}$($ A[0..m-1] $)
  
  $\texttt{StoogeSort}$($ A[n-m..n-1] $)
  
  $\texttt{StoogeSort}$($ A[0..m-1] $)
2. $m = \lceil 2n / 3 \rceil$ の部分を $m = \lfloor 2n / 3 \rfloor$ にしたときに $\textsc{StoogeSort}$ が正しく動くかどうかを答え、それが正しいことを示してください。
3. $\textsc{StoogeSort}$ が実行するベースケースを含んだ比較演算の回数についての再帰方程式を示してください。
4. 再帰方程式を解いて、解が正しいことを証明してください。 [ヒント: 天井関数は無視できます。]
5. $\textsc{StoogeSort}$ で実行される swap の回数が最大 $\binom{n}{2}$ 回であることを示してください。
次の冷酷で異常な (cruel and unusual) ソートアルゴリズムは Gary Miller (ゲイリー・ミラー) によって提案されました。

このアルゴリズムで行われる比較演算の回数は入力の配列に依存していません。このようなソートアルゴリズムのことを無神経 (oblivious) であると言います。
1. $\textsc{Cruel}$ が入力の配列を正しくソートすることを帰納法で示してください。 [ヒント: 1, 2, 3, 4 を $n/4$ 個ずつ持つ長さ $n$ の配列を考えてください。なぜこれだけを考えれば十分なのでしょうか？]
2. $\textsc{Unusual}$ から for ループを取り除くと $\textsc{Cruel}$ が正しく動かなくなることを示してください。
3. $\textsc{Unusual}$ の最後の二行を交換すると $\textsc{Cruel}$ が正しく動かなくなることを示してください。
4. $\textsc{Unusual}$ の実行時間を求めて、それを証明してください。
5. $\textsc{Cruel}$ の実行時間を求めて、それを証明してください。
procedure $\texttt{Cruel}$($ A[1..n] $)

if $ n > 1 $ then

$\texttt{Cruel}$($ A[1..n/2] $)

$\texttt{Cruel}$($ A[n/2 + 1..n] $)

$\texttt{Unusual}$($ A[1..n] $)

procedure $\texttt{Unusual}$($A[1..n]$)

if $ n = 2 $ then

if $ A[1] > A[2] $ ⟨⟨唯一の比較！⟩⟩ then

swap $ A[1] \leftrightarrow A[2] $

else

⟨⟨$A$ を $4$ 分割して⟩⟩

⟨⟨$2$ 番目と $3$ 番目を入れ替える⟩⟩

for $ i \leftarrow 1 $ to $ n / 4 $ do

swap $ A[i + n/4] \leftrightarrow A[i + n/2] $

⟨⟨左半分に対する再帰⟩⟩

$\texttt{Unusual}$($ A[1..n/2] $)

⟨⟨右半分に対する再帰⟩⟩

$\texttt{Unusual}$($ A[n/2+1..n] $)

⟨⟨中央半分に対する再帰⟩⟩

$\texttt{Unusual}$($ A[n/4+1..n/4] $)
配列 $A[1..n]$ の転置 (inversion) とは、添え字の組 $(i, j)$ であって $i < j$ かつ $A[i] > A[j]$ を満たすものを言います。$n$ 要素の配列の転置の数は $0$ (配列がソートされているとき) から $\binom{n}{2}$ (配列が逆順にソートされているとき) までの値を取ります。$n$ 要素の配列を入力として受け取って、その配列の転置の数を $O(n \log n)$ 時間で計算するアルゴリズムを説明、解析してください。 [ヒント: マージソートを改変してください。]
1. 直線 $y=0$ 上の点 $\lbrace p_{1}, p_{2}, \ldots, p_{n} \rbrace$ と直線 $y=1$ 上の点 $\lbrace q_{1}, q_{2}, \ldots, q_{n} \rbrace$ が与えられたとします。$p_{i}$ と $q_{i}$ を結んで $n$ 本の直線を引いたときに、これらの直線が作る交点の数を $O(n\log n)$ 時間で求める分割統治アルゴリズムを説明、解析してください。 [ヒント: 前問と似ています。]
  
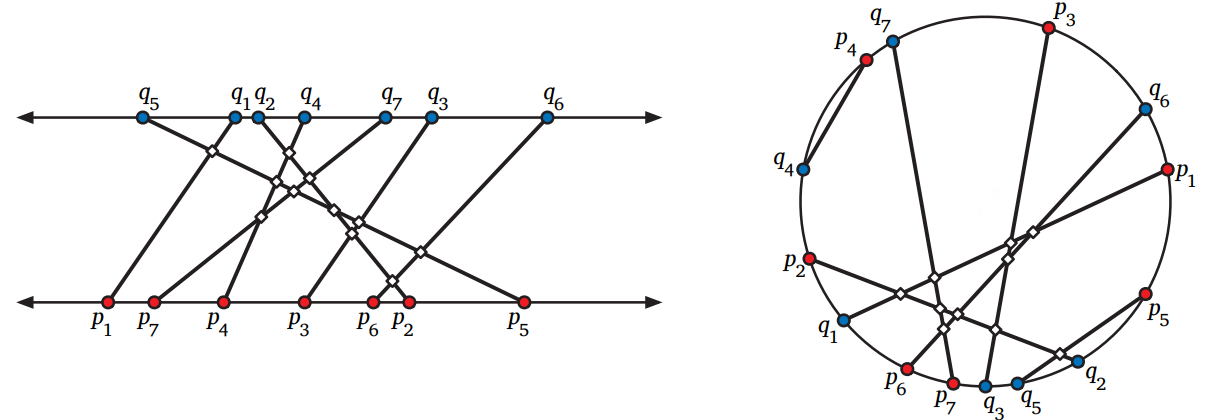  図 1.20
  
  平行な直線の間にかかった直線とそれによってできる 11 個の交点 (左)、および単位円周の中にかかった直線とそれによってできる 10 個の交点 (右)
2. 今度は $\lbrace p_{1}, p_{2}, \ldots, p_{n} \rbrace$ と $\lbrace q_{1}, q_{2}, \ldots, q_{n} \rbrace$ が単位円周上の点として与えられたとします。$p_{i}$ と $q_{i}$ を結んで $n$ 本の直線を引いたときに、これらの直線が作る交点の数を $O(n\log^{2} n)$ 時間で求める分割統治アルゴリズムを説明、解析してください。 [ヒント: (a) を使います。]
3. ❤ (b) で考えた問題に対する $O(n\log n)$ 時間のアルゴリズムを説明、解析してください。
1. 配列 $A[1..n]$ に対して、小配列 $A[k+1..k+\sqrt{n}]\ (k = 0 \ldots n - \sqrt{n})$ をソートするサブルーチンを $\textsc{SqrtSort}$ とします (簡単のために、ある整数 $k$ に対して $n = k^{2}$ とします)。この $\textsc{SqrtSort}$ サブルーチンだけを使って $n$ 要素の配列を正しくソートするアルゴリズムを説明してください。ただし、配列の検査、改変は必ず $\textsc{SqrtSort}$ を使って行わなければならず、要素を直接比較、移動、複製することは許されません。最悪ケースでは $\textsc{SqrtSort}$ は何回呼ばれますか？
2. ♣ (a) で答えたアルゴリズムが定数倍を無視すれば最適であることを示してください。つまり、アルゴリズムが $\textsc{SqrtSort}$ を呼ぶ回数を $f(n)$ としたときに、$\textsc{SqrtSort}$ を $o(f(n))$ 回使って配列をソートするアルゴリズムが存在しないことを示してください。
3. $\textsc{SqrtSort}$ が (a) の答えのアルゴリズムを使って再帰的に実装されているとします。例えば二段階目の再帰呼び出しでは、アルゴリズムの入力の長さは約 $n^{1 / 4}$ となります。このソートアルゴリズムの最悪計算時間を求めてください。(解析を簡単にするために、配列の大きさが $2^{2^{k}}$ という形であり、ルートの値がいつも整数であると仮定して構いません)。
${}$
選択
価値 (value) と重さ (weight) を持つ要素が $n$ 個入った集合 $S$ が与えられたとします。各 $x \in S$ に対して、次のように $S$ の部分集合を定義します。
- $S_{< x}$ は価値が $x$ の価値よりも小さい $S$ の要素からなる集合。
- $S_{> x}$ は価値が $x$ の価値よりも大きい $S$ の要素からなる集合。
$S$ の部分集合 $R \subseteq S$ に対して、$w(R)$ で $R$ の要素の重さの和を表すことにします。$S$ の重み付き中央値 (weighted median) とは、$S$ の要素 $x$ であって $w(S_{< x}) \leq w(S) / 2$ かつ $w(S_{> x}) \leq w(S) / 2$ を満たすものを言います。

重み付けされた要素が $n$ 個入った集合を受け取って、その集合の重み付き中央値を $O(n)$ 時間で計算するアルゴリズムを説明、解析してください。アルゴリズムの入力は二つの配列 $S[1..n]$ と $W[1..n]$ であり、添え字 $i$ について、$i$ 番目の要素は価値 $S[i]$ と重み $W[i]$ を持つとします。同じ価値を持つ要素は無く、重みは全て正であると仮定して構いません。
1. 入力として受け取った配列 $A[1..n]$ の中に同じ要素が $n/4$ 個以上あるかどうかを $O(n)$ 時間で判定するアルゴリズムを説明してください。
2. 入力として $A[1..n]$ と $k$ を受け取って、$A$ の中に同じ要素が $k$ 個以上あるかどうかを判定するアルゴリズムを説明、解析してください。アルゴリズムの実行時間を $n$ と $k$ の関数として表してください。
ハッシュソートや基数ソートなどの、入力の (順番ではなく) 値に依存するアルゴリズムを用いてはいけません。
配列 $A[1..5]$ が同じ要素を持たないときに、$A$ の中央値を最大 6 回の比較を使って求めるアルゴリズムを説明してください。説明には疑似コードではなくて決定木を使ってください。決定木は頂点が "$A[i] \lessgtr A[j]$" の形をしていて、葉が配列の添え字を表します。

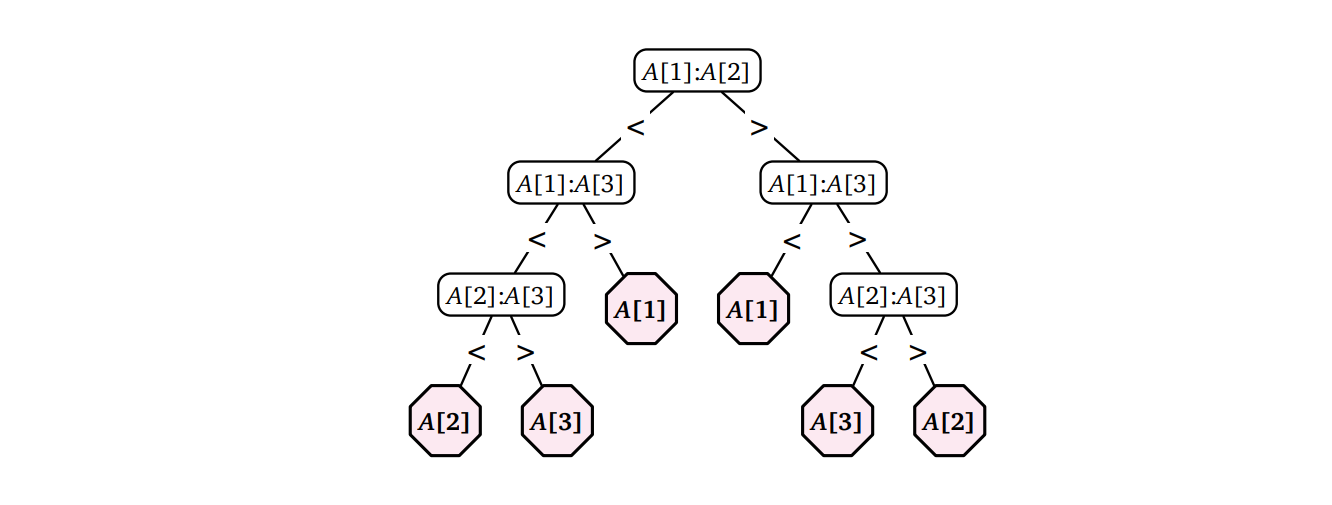図 1.21

三要素の配列の中央値を最大三回の比較を使って求める
次に示す、Blum-Floyd-Pratt-Rivest-Tarjan の $\textsc{MomSelect}$ アルゴリズムを一般化したものを考えます。このアルゴリズムは基本的に $\textsc{MomSelect}$ と同じですが、入力の配列を長さ 5 のブロック $\lceil n / 5 \rceil$ 個ではなく長さ $b$ のブロック $\lceil n/b \rceil$ 個に分割する点が異なります。
1. $b$ が定数だと仮定したとき ($\textsc{MedianOfB}$ が $O(1)$ 時間で実行されるとき) のアルゴリズムの実行時間に関する再帰方程式を示してください。再帰的に解く小問題の大きさは $b$ にどのように依存していますか？ $b$ が偶数の場合と奇数の場合を別々に考えること。
2. $\textsc{Mom1Select}$ の最悪計算時間を求めてください。 [ヒント: ひっかけ問題です。]
3. ♣ ❤ $\textsc{Mom2Select}$ の最悪計算時間を求めてください。 [ヒント: さらなるひっかけ問題です！]
4. ❤ $\textsc{Mom3Select}$ の最悪計算時間を求めてください。計算時間の上界はすぐに求まりますが、本当に難しいのはその解析が正しいと証明する部分です。 [ヒント: 練習問題 1.10]
5. ❤ $\textsc{Mom4Select}$ の最悪計算時間を求めてください。ここでも、難しいのは答えがこれ以上改善できないと示す部分です¹⁸。
6. 定数 $b \geq 5$ について、$\textsc{MomBSelect}$ の実行時間は $O(n)$ となります。しかし定数部分の値は $b$ によって異なります。
  
  $b$ 個の数字の中央値を計算するのに必要な比較演算の回数の最小値を $M(b)$ とすると、$M(b)$ の正確な値は $b \leq 13$ までしか知られていません。 \[ \begin{array}{r|rrrrrrrrrrrrr} b & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ \hline M(b) & 0 & 1 & 3 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20 & 23 \end{array} \]
  
  5 から 13 までの $b$ について、$\textsc{MomBSelect}$ の実行時間の上界を定数 $\alpha_{b}$ を使って $T(n) \leq \alpha_{b} n$ の形で求めてください (例えば本文中では $\alpha_{b} \leq 16n$ を示しました)。
7. $\alpha_{b}$ が最小となる $b$ を求めてください [ヒント: ひっかけ問題です！]
procedure $\texttt{MomBSelect}$($A[1..n], k$)

if $ n \leq \color{red}{b^{2}} $ then

総当たりで中央値を求める

else

$ m \leftarrow \color{red}{\lceil n / b \rceil} $

for $ i \leftarrow 1 $ to $m$ do

$ M[i] \leftarrow $$\texttt{MedianOfB}$($ \color{red}{A[b(i-1)+1..bi]} $)

$ \mathit{mom}_{\color{red}{b}} \leftarrow $$\texttt{MomBSelect}$($ M[1..m], \lfloor m/2 \rfloor $)

$ r \leftarrow $$\texttt{Partition}$($ A[1..n], \mathit{mom}_{\color{red}{b}} $)

if $k < r$ then

return $\texttt{MomBSelect}$($ A[1..r-1], k $)

else if $k > r$ then

return $\texttt{MomBSelect}$($ A[r+1..n], k-r $)

else

return $ \mathit{mom}_{\color{red}{b}} $

図 1.22

パラメータ化された選択アルゴリズムのクラス
次に示す Blum-Floyd-Pratt-Rivest-Tarjan の $\textsc{MomSelect}$ アルゴリズムの変種の実行時間が $O(n)$ であることを示してください。このアルゴリズムでは入力の配列に使うピボットを選ぶときの処理が一段階追加されています。

procedure $\texttt{MommomSelect}$($ A[1..n], k $)

if $ n \leq 81 $ then

総当たりで中央値を求める

else

$ m \leftarrow \lceil n / 3 \rceil $

for $ i \leftarrow 1 $ to $m$ do

$ M[i] \leftarrow $$\texttt{MedianOf3}$($ A[3i-2..3i] $)

$ mm \leftarrow \rceil m / 3 \rceil $

for $ j \leftarrow 1 $ to $mm$ do

$ \mathit{Mom}[j] \leftarrow $$\texttt{MedianOf3}$($ M[3j-2..3j] $)

$ \mathit{momom} \leftarrow $$\texttt{MomomSelect}$($ \mathit{Mom}[1..mm], \lfloor mm/2 \rfloor $)

$ r \leftarrow $$\texttt{Partition}$($ A[1..n], \mathit{momom} $)

if $k < r$ then

return $\texttt{MomomSelect}$($ A[1..r-1], k $)

else if $k > r$ then

return $\texttt{MomomSelect}$($ A[r+1..n], k-r $)

else

return $ \mathit{momom} $

図 1.23

mom の中央値を使った選択
1. 二つのソートされた配列 $A[1..n]$ と $B[1..n]$ が与えられたとき、$A$ と $B$ の和集合の中央値を $O(\log n)$ 時間で求めるアルゴリズムを説明してください。二つの配列には同じ要素が含まれないと仮定して構いません。
2. 二つのソートされた配列 $A[1..m]$ と $B[1..n]$ と整数 $k$ が与えられたときに、$A \cup B$ で $k$ 番目に小さい要素を $O(\log (m + n))$ 時間で求めるアルゴリズムを説明してください。例えば、$k = 1$ のとき、このアルゴリズムは $A \cup B$ の最小値を計算します。 [ヒント: (a) の答えを使います。]
3. ❤ 三つのソートされた配列 $A[1..n]$, $B[1..n]$, $C[1..n]$ と整数 $k$ が与えられたときに、$A \cup B \cup C$ から $k$ 番目に小さい整数を $O(\log n)$ 時間で求めるアルゴリズムを説明してください。
4. 最後に、二次元配列 $A[1..m,1..n]$ の各列 $A[i,\cdot]$ がソートされているときに、この二次元配列 $A$ と整数 $k$ を受け取って $A$ から $k$ 番目に小さい要素をできるだけ速く取り出すアルゴリズムを説明してください。アルゴリズムの実行時間は $m$ にどのように依存しますか？ [ヒント: 練習問題 1.16 を先に解いてください。]
${}$

算術
1854 年、1 から 59 までの整数の二乗が刻まれた紀元前 2000 年ごろのシュメールの粘土板が考古学者によって発見されました。この発見を持ってシュメール人が掛け算をするときには $x \cdot y = (x^{2} + y^{2} - (x-y)^{2}) / 2$ などの等式を用いた二乗への帰着が使われていたとする考古学者もいます。しかし残念ながら、そのような主張をする学者はシュメール人が大きな数字の二乗をどのように求めていたかについては口を閉ざしています。

粘土板が刻まれてから 4000年後の私たちは、再帰の力を使うことでシュメール人数学者を重労働から救うことができます！
1. Karatsuba のアルゴリズムを変更して、$n$ 桁の数の二乗の計算を、$\lceil n / 2 \rceil$ 桁の数の二乗の計算三つに帰着させることで $O(n^{\lg 3})$ 時間で行うアルゴリズムを作ってください (1960 年に Karatsuba がまさに行ったことです)。
2. $n$ 桁の数の二乗の計算を、$\lceil n / 3 \rceil$ 桁の数の二乗の計算六つに帰着させることで $O(n^{\log_{3} 6})$ 時間で計算するアルゴリズムを説明してください。
3. ❤ $n$ 桁の数の二乗の計算を、$(n/3 + O(1))$ 桁の二乗の計算五つに帰着させることで $O(n^{\log_{3} 5})$ 時間で計算するアルゴリズムを説明してください。 [ヒント: $(a + b + c)^{2} + (a - b + c)^{2}$ の値は何ですか？]
1. Karatsuba のアルゴリズムを変更して、$n \geq m$ のときに $m$ 桁の数と $n$ 桁の数の積を $O(nm^{\lg3 - 1})$ 時間で計算するアルゴリズムを作ってください。
2. $2^{n}$ の十進表記を $O(n^{\lg3})$ 時間で求めるアルゴリズムを (a) の答えをサブルーチンとして使って説明してください (答えを一桁ずつ計算する通常のアルゴリズムの実行時間は $\Theta(n^{2})$ です)。
3. $n$ 桁の二進数で表記された任意の数の十進表記を $O(n^{\lg 3})$ で求める分割統治アルゴリズムを説明してください。 [ヒント: 実行時間に追加される log の係数に注意してください。]
4. ❤ 二つの $n$ 桁の数の積を $O(M(n))$ 時間で計算できるとします。二進表記で $n$ 桁の任意の数の十進表記を $O(M(n) \log n)$ 時間で求めるアルゴリズムを説明してください。 [ヒント: 実行時間の解析は難しいです。定義域変換を使ってください。]
非負の整数 $n$ に対して階乗 $n!$ を計算する、次の古典的な再帰アルゴリズムを考えます。

procedure $\texttt{Factorial}$($n$)

if $n = 0$ then

return $1$

else

return $n \cdot {}$$\texttt{Factorial}$($n - 1$)
1. このアルゴリズムが行う乗算の回数を求めてください。
2. $n!$ を二進表記で書くために必要なビット数を求めてください。答えは適当な関数 $f(n)$ を使って $\Theta(f(n))$ の形で書いてください。 [ヒント: $(n/2)^{n/2} < n! < n^{n}$]
3. (b) の答えから、$\textsc{Factorial}$ の実行時間を乗算の数で測っても意味がないことが分かるでしょう。格子アルゴリズムまたは duplation と mediation のアルゴリズムを使えば、任意の $k$ 桁の数と $l$ 桁の数の積を $O(k \cdot l)$ 時間で計算できます。この乗算アルゴリズムをサブルーチンとして使ったときの $\textsc{Factorial}$ の実行時間を求めてください。
4. 次の再帰的なアルゴリズムも階乗を計算しますが、積の順番が異なります。
  
  ⟨⟨$n! / (n-m)!$ を計算する⟩⟩
  
  procedure $\texttt{Falling}$($n, m$)
  
  if $m = 0$ then
  
  return $1$
  
  else if $m = 1$ then
  
  return $n$
  
  else
  
  return $\texttt{Falling}$($n, \lfloor m / 2 \rfloor$) ${} \cdot {}$$\texttt{Falling}$($n - \lfloor m / 2 \rfloor, \lceil m / 2 \rceil$)
  
  小学校で使う掛け算アルゴリズムを使ったときの $\textsc{Falling}(n, n)$ の実行時間を求めてください。
5. Karatsuba のアルゴリズムを変更して、$k \geq l$ のときに $k$ 桁の数と $l$ 桁の数の積を $O(k \cdot l^{\lg 3 - 1}) \approx O(k \cdot l^{0.585})$ 時間で計算するアルゴリズムを説明、解析してください。
6. ❤ (e) で示した Karatsuba の乗算アルゴリズムを使ったときの $\textsc{Factorial}(n)$ および $\textsc{Falling}(n, n)$ の実行時間を求めてください。
正の整数 $x, y$ の最大公約数 (greatest common divisor) とは $x / d$ と $y / d$ がともに整数となる最大の整数 $d$ のことであり、$\gcd (x, y)$ と表記します。紀元前 300 年ごろに書かれた Euclid の『原論』では、$\gcd (x,y)$ を計算する次の再帰的アルゴリズムが説明されています¹⁹:

procedure $\texttt{EuclidGCD}$($x, y$)

if $x = y$ then

return $x$

else if $x > y$ then

return $\texttt{EuclidGCD}$($x - y, y$)

else

return $\texttt{EuclidGCD}$($x, y - x$)
1. $\textsc{EuclidGCD}$ が $\gcd (x, y)$ を正しく計算することを証明してください²⁰。具体的には、次のことを示してください:
  - $\textsc{EuclidGCD}(x, y)$ が $x$ と $y$ を割り切ること
  - $x, y$ に共通する約数が $\textsc{EuclidGCD}(x, y)$ の約数であること
2. $\textsc{EuclidGCD}$ の最悪計算時間を $x, y$ の関数として求めてください ($x - y$ の計算には $O(\log x + \log y)$ 時間かかるとします)。
3. 次のアルゴリズムが $\gcd (x, y)$ を計算することを示してください。
  
  procedure $\texttt{FastEuclidGDC}$($x, y$)
  
  if $y = 0$ then
  
  return $x$
  
  else if $x > y$ then
  
  return $\texttt{FastEuclidGDC}$($y, x \text{ mod } y$)
  
  else
  
  return $\texttt{FastEuclidGDC}$($x, y \text{ mod } x$)
4. $\textsc{FastEuclidGCD}$ の最悪計算時間を $x, y$ の関数として求めてください ($x \text{ mod } y$ の計算には $O(\log x \cdot \log y)$ 時間かかるとします)。
5. 次のアルゴリズムが $\gcd (x, y)$ を計算することを示してください。
  
  procedure $\texttt{BinaryGCD}$($x, y$)
  
  if $x = y$ then
  
  return x
  
  else if $x$ と $y$ がどちらも偶数 then
  
  return $2 \cdot $$\texttt{BinaryGCD}$($x/2, y/2$)
  
  else if $x$ が偶数 then
  
  return $\texttt{BinaryGCD}$($x/2, y$)
  
  else if $y$ が偶数 then
  
  return $\texttt{BinaryGCD}$($x, y/2$)
  
  else if $x > y$ then
  
  return $\texttt{BinaryGCD}$($(x - y)/2, y$)
  
  else
  
  return $\texttt{BinaryGCD}$($x, (y - x)/2$)
6. $\textsc{BinaryGCD}$ の最悪計算時間を $x, y$ の関数として求めてください ($x - y$ の計算には $O(\log x + \log y)$ 時間、$z/2$ の計算には $O(\log z)$ 時間かかるとします)。
${}$

配列
$2^{n} \times 2^{n}$ の格子盤から (任意の位置の) マスを一つだけ取り除いたとします。この格子盤に三つのマスからなる L 字型のタイルを敷き詰める方法を計算するアルゴリズムを説明、解析してください。アルゴリズムの入力は整数 $n$ と穴の開いたマスの座標を表す $n$ ビットの整数二つであり、出力は $(4^{n} - 1)/3$ 個のタイルの座標と方向です。アルゴリズムの実行時間は $O(4^{n})$ としてください。 [ヒント: まずそのような敷き詰め方が常に存在することを示してください。]
$n$ 人の代議員の参加する政党大会 (あるいは教授会) に参加したとします。代議員はちょうど一つの政党に所属していますが、議員に所属政党を直接尋ねると大会からつまみ出されてしまうので、どの議員がどの政党に属しているかを見分けることはできません。しかし、二人の議員が同じ政党に属しているかどうかは見分けることができます。議員同士を対面させたときに、同じ政党の議員同士は必ず笑顔で握手を交わしながら挨拶するのに対して、異なる政党の議員同士は殺気立った目線と礼儀を欠いた態度で挨拶をするからです²¹。
1. 半分以上の代議員が同じ政党に所属している場合に、この政党の議員を全員特定する効率の良いアルゴリズムを説明してください。
2. 政党が三つ以上あり、その一つが最高得票数を持つ、つまり他の全ての政党よりも多く代議員を持つとします。この政党に所属する議員を極限まで少ない労力で特定する実践的な手続きを提示してください。最高得票数を持つ政党は少なくとも $p$ 人からなるとします。どうかお願いします。
Smullyan (スマリヤン) 島には三種類の住人がいます: 常に真実を話す騎士、常に嘘をつく悪党、そして真実を話すこともあれば嘘をつくこともある一般人です。島の住人はみな住民全員の名前と種類 (騎士、悪党、一般人) を知っています。あなたは住人全員の種類を知りたいとします。

島の住人に聞くことができるのは他の住人の種類だけです。つまり「X さん、こんにちは。Y の種類を教えてください」と尋ねることができ、答えは次のようになります:
- X が騎士なら、X は Y の正しい種類を答える。
- X が悪党なら、X は Y の正しい種類でない二つの種類のうちどちらかを答える。
- X が一般人なら、X は三つの種類の全てを答える可能性がある。
この形でない質問を島の住人にしても無視されます。したがって住人に自分自身の種類について聞くことはできません。また住人は同じ質問に対して同じ答えを返すので、同じ質問を何度も尋ねる意味はありません。
1. 住民の (狭義) 過半数が騎士であることを知っている場合に、住民全員の種類を決定する効率の良いアルゴリズムを説明してください。
2. 騎士が住民の過半数を占めていない場合には、住民全員の種類を決定できないことを示してください。
ほとんどのグラフィックスハードウェアでは blit (block transfer) と呼ばれる低レベル命令が利用できます。blit 命令とは四角形のピクセルマップ (ピクセルの値の二次元配列) のチャンクをコピーする命令であり、 C のライブラリ関数 memcpy() の二次元版と言うことができます。

$n \times n$ のピクセルマップを時計回りに $90^{\circ}$ 回転させたいとします。$n$ が $2$ のべきの場合には、ピクセルマップを四つの $n / 2 \times n / 2$ ブロックに分け、各ブロックを五回の blit 命令で正しい位置に移動させ、それぞれのブロックを再帰的に回転させることで回転を行うことができます (blit 命令が五回なのは、Hanoi の塔パズルが杭を三つ必要としたのと同じ理由です)。あるいは、最初に再帰的に回転させてから blit で正しい位置に移動させるということもできます。

図 1.24

ピクセルマップを回転させる二つのアルゴリズム
1. $n$ が $2$ のべきのときに、両方のバージョンのアルゴリズムが正しいことを証明してください。
2. $n$ が $2$ のべきのときに、blit 命令が実行される回数を求めてください。
3. $2$ のべきではない任意の $n$ についても正しく実行されるようにはアルゴリズムをどう改変すればよいか説明してください。改変されたアルゴリズムにおいて blit は何回実行されますか？
4. $k \times k$ の blit 命令の実行時間が $O(k^{2})$ である場合、(c) で答えたアルゴリズムの実行時間を求めてください。
5. $k \times k$ の blit 命令の実行時間が $O(k)$ の場合はどうなりますか？²²
異なる $n$ 個の要素からなる配列 $A[0..n-1]$ がバイトニック(bitonic) であるとは、添え字の組 $i, j$ であって $A[(i - 1) \text{ mod } n] <$ $A[i] > A[(i + 1) \text{ mod } n]$ かつ $A[(j - 1) \text{ mod } n] >$ $A[j] < A[(j + 1) \text{ mod } n]$ を満たすものがちょうど一つ存在することを言います。言い換えると、要素を最初からたどっていったときに最初は順に大きくなり、ある要素からは順に小さくなる配列、または環状にシフトするとそのような配列になる配列がバイトニックな配列です。例えば:
- $[4\ 6\ 9\ 8\ 7\ 5\ 1\ 2\ 3]$ はバイトニックです。
- $[3\ 6\ 9\ 8\ 7\ 5\ 1\ 2\ 4]$ はバイトニックではありません。
バイトニックな長さ $n$ の配列から最小要素を $O(\log n)$ 時間で取り出すアルゴリズムを説明、解析してください。入力配列に入っている数には重複がないことを仮定して構いません。
異なる $n$ 個の整数からなるソートされた配列 $A[1..n]$ が与えられたとします。$A$ の要素は負またはゼロまたは正の整数であり、$A[1] < A[2] < \cdots < A[n]$ とソートされているとします。
1. $A[i] = i$ を満たす添え字 $i$ が存在するなら $i$ を計算し、存在しないならそのことを答える高速なアルゴリズムを説明してください。
2. $A[1] > 0$ であることが事前にわかっているとします。$A[i] = i$ を満たす添え字 $i$ が存在するなら $i$ を計算し、存在しないならそのことを答える高速なアルゴリズムを説明してください。 [ヒント: この問題は超簡単です。]
配列 $A[1..n]$ が $A[1] \geq A[2]$ と $A[n-1] \leq A[n]$ を満たしているとします。要素 $A[x]$ が極小であるとは、$A[x]$ の隣の要素が両方とも $A[x]$ より大きいことを言います。きちんと言うと、$A[x - 1] \geq A[x]$ かつ $A[x] \leq A[x + 1]$ だということです。例えば次の配列には六つの極小値があります: \[ 9\ {\color{#B52F1B}{7}}\ 7\ 2\ {\color{#B52F1B}{1}}\ 3\ 7\ 5\ {\color{#B52F1B}{4}}\ 7\ {\color{#B52F1B}{3}}\ {\color{#B52F1B}{3}}\ 4\ 8\ {\color{#B52F1B}{6}}\ 9 \] 配列を順番に探索すれば極小値の一つを $O(n)$ 時間で見つけることができるのは明らかです。極小値の一つを $O(\log n)$ 時間で求めるアルゴリズムを説明、解析してください。 [ヒント: 与えられた境界条件の下では配列には少なくとも一つの極小値が含まれます。なぜでしょうか？]
ソートされた長さ $n$ の配列を $k\ (= 1 \ldots n - 1)$ 回シフトしたものが与えられたとします。つまり、最初の部分 $A[1..k]$ は昇順に、後ろの部分 $A[k+1..n]$ は降順にソートされていて、かつ $A[n] < A[1]$ だということです。ここで $k$ は未知数です。

例えば、次の 16 要素の配列が与えられます ($k = 10$ です): \[ 9\ 13\ 16\ 18\ 19\ 23\ 28\ 31\ 37\ 42\ |\ 1\ 3\ 4\ 5\ 7\ 8 \]
1. 未知の整数 $k$ を求めるアルゴリズムを説明、解析してください。
2. 入力として受け取る $x$ が $A$ に含まれるかどうかを判定するアルゴリズムを説明、解析してください。
大ヒットアクション映画 Fast and Impossible XIII $\frac{3}{4}$: The Last Guardians of Expendable Justice Reloaded の第二幕の終盤で、悪役の Dr. Metaphor がヒーロー全員に催眠術をかけるシーンがあります。その上で Dr. Metaphor はヒーローたちを崖際に一列に並ばせ、合図とともに自分の右および左にいるヒーローの中で、一番近くにいる自分よりも背が高いヒーローを両方銃で撃つように命じました。

$n$ 人のヒーローの背の高さが左から右に $\mathit{Ht}[1..n]$ で与えられるとします (給料の支払いで揉めないように、プロデューサーは同じ背の高さのヒーローを雇いませんでした)。次の総当たりアルゴリズムを使えば、各ヒーローの左右の標的を $O(n^{2})$ 時間で求めることができます:

procedure $\texttt{WhoTargetsWhom}$($\mathit{Ht}[1..n]$)

for $j \leftarrow 1$ to n do

⟨⟨ヒーロー $j$ の左の標的 $L[j]$ を求める⟩⟩

$L[j] \leftarrow \textsc{None}$

for $i \leftarrow 1 $ to $j - 1$ do

if $\mathit{Ht}[i] > \mathit{Ht}[j]$ then

$L[j] \leftarrow i$

⟨⟨ヒーロー $j$ の右の標的 $R[j]$ を求める⟩⟩

$R[j] \leftarrow \textsc{None}$

for $k \leftarrow n $ downto $j + 1$ do

if $\mathit{Ht}[k] > \mathit{Ht}[j]$ then

$R[j] \leftarrow k$

return $L[1..n],\ R[1..n]$
1. $\textsc{WhoTargetsWhom}$ の出力を $O(n \log n)$ 時間で計算する分割統治アルゴリズムを説明してください。
2. $n$ 人のヒーローのうち少なくとも $\lfloor n / 2 \rfloor$ 人が誰かの標的になることを示してください。つまり、出力の配列 $R[0..n-1]$ と $L[0..n-1]$ の中には ($\textsc{None}$ でない) 異なる値が少なくとも $\lfloor n / 2 \rfloor$ 個含まれることを示してください。
3. あぁ、なんということでしょう。Dr. Metaphor の極悪非道な計画は実行されました。合図とともに全てのヒーローは標的に向かって銃を撃ち、打たれたヒーローは崖から落ちていきました。助からないでしょう。さらに、この卑劣な実験は何度も繰り返されました。Dr. Metaphor は殺戮が終わるたびに生き残ったヒーローたちに新しい標的を選ばせ、合図を送って銃を撃たせました。そうして、最終的には背が一番低いヒーローが生き残りました²³。
  
  シーンが終了するまでに Dr. Metaphor が合図を鳴らす回数を計算するアルゴリズムを説明、解析してください。満点を得るためには、アルゴリズムの実行時間が $O(n)$ であることが求められます。
あなたは人気テレビ番組 "お隣さんを倒せ！" に参加しました。あなたの前には $m \times n$ の格子があって、各マスには異なる番号が書かれています。このゲームの目標は上下左右のマスよりも大きな値を持つマスを見つけることであり、一つのマスの値を確認するには $100 かかります。対戦相手よりも少ない金額でそのようなマスを見つければ勝ちで、ラスベガスへのペア旅行券と、誰もが喉から手が出るほど欲しがっている Rice-A-Roni™ 一年分を獲得できます。
1. $m = 1$ とします。左右のマスよりも値が大きいマスを見つけるアルゴリズムを説明してください。最悪ケースではマスをいくつ開けることになりますか？
2. ❤ $m = n$ とします。上下左右のマスよりも値が大きいマスを見つけるアルゴリズムを説明してください。最悪ケースではマスをいくつ開けることになりますか？
3. ♣ ❤ (b) の答えが定数倍を無視すれば最良であることを証明してください。
1. $l$ を正の整数とします。$n = 2^{l} - 1$ として、異なる $l$ ビットバイナリ文字列の配列 $A[1..n]$ が与えられたとします。つまり、ちょうど一つの $l$ ビットバイナリ文字列が $A$ に含まれていないということです。$A$ にアクセスする方法が $A[i]$ の第 $j$ ビットを $O(1)$ 時間で取得する関数 $\textsc{FetchBit}(i, j)$ だけに限られているとしたとき、$A$ に含まれない唯一の文字列を $O(n)$ 回の $\textsc{FetchBit}$ の呼び出しで見つけるアルゴリズムを説明してください。
2. $k, l$ を正の整数として $n = 2^{l} - k$ とします。そして前問と同じように $A[1..n]$ に異なる $l$ ビットバイナリ文字列が入っているとします。 $A$ に入っていない $k$ 個の文字列を $O(n \log k)$ 回の $\textsc{FetchBit}$ の呼び出しで見つけるアルゴリズムを説明してください。
${}$

木
この問題では、二分木に含まれる任意の連結部分グラフを部分木と呼びます。二分木が完全であるとは、全ての葉でない頂点がちょうど二つの子を持ち、全ての葉が同じ深さを持つことを言います。与えられた二分木に含まれる最大完全部分木を計算する再帰的なアルゴリズムを説明、解析してください。アルゴリズムの出力は部分木の根と深さです。次の図に例を示します。

$この二分木の最大完全部分木の高さは $3$$

図 1.26

この二分木の最大完全部分木の高さは $3$
$T$ を $n$ 頂点の二分木とします。 $T$ から頂点 $v$ を取り除くと最大で三つの部分木が生じます。つまり、左の子を含む部分木、右の子を含む部分木、そして親を含む部分木です。頂点 $v$ が中心であるとは、$v$ を取り除くことによって生じる部分木がどれも $n / 2$ 以下の頂点しか持たないことを言います。次の図に例を示します。

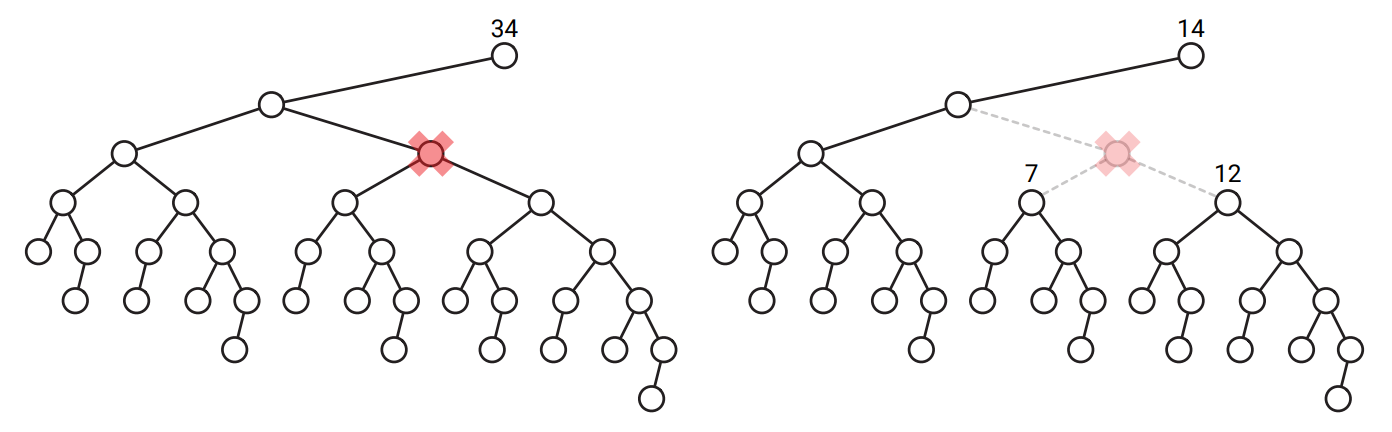$$34$ 頂点の二分木から中心の頂点を取り除くと、頂点数が $14$, $7$, $12$ の部分木が残る$

図 1.27

$34$ 頂点の二分木から中心の頂点を取り除くと、頂点数が $14$, $7$, $12$ の部分木が残る

任意の二分木を受け取ってその中心の頂点を見つけるアルゴリズムを説明、解析してください。 [ヒント: まずどんな木にも中心があることを示してください。]
1. George O'Jungle 教授はある二分木を持っています。その二分木には頂点が 27 個あり、各頂点がアルファベットおよび "&" でユニークにラベル付けされています。行きがけ順 (preorder) および帰りがけ順 (postorder) でこの二分木を走査すると、頂点が次の順番に並ぶそうです:
  - 行きがけ順: I Q J H L E M V O T S B R G Y Z K C A & F P N U D W X
  - 帰りがけ順: H E M L J V Q S G Y R Z B T C P U D N F W & X A K O I
  教授の持っている二分木を復元してください。
2. 全二分木 (full binary tree) とは全ての葉でない頂点が二つの子を持つ二分木のことです。
  1. 任意の全二分木の行きがけ順および帰りがけ順の走査結果からを元の全二分木を復元する再帰的なアルゴリズムを説明、解析してください。
  2. 任意の二分木の行きがけ順および帰りがけ順の走査結果からを元の二分木を復元するアルゴリズムが存在しないことを示してください。
3. 任意の二分木の行きがけ順および通り掛け順 (inorder) の走査結果から元の二分木を復元するアルゴリズムを説明、解析してください。
4. 任意の二分探索木の行きがけ順の走査結果だけを使って、元の二分探索木を復元するアルゴリズムを説明、解析してください。
5. ❤ 任意の二分探索木の行きがけ順の走査結果だけを使って、元の二分探索木を $\pmb{O(n)}$ 時間で復元するアルゴリズムを説明、解析してください。
(b) - (e) では、二分木のキーは全て異なっていて、入力は少なくとも一つの二分木を表していると仮定して構いません。
二次元の領域内に $n$ 個の点が与えられたとします。kd-木 (kd-tree) はこれらの点を次のように再帰的に分割します。まず領域の内部に点が無いならば、それで終わりです。そうでないなら、点の一つを通る垂直な直線によって点の数がなるべく等しくなるように領域を二つに分けます。その後領域を 90 度回転させてから、再帰的に分割を行います。これによって、垂直方向と水平方向の分割が交互に起きます。最後に残る空領域のことをセル (cell) と言います。

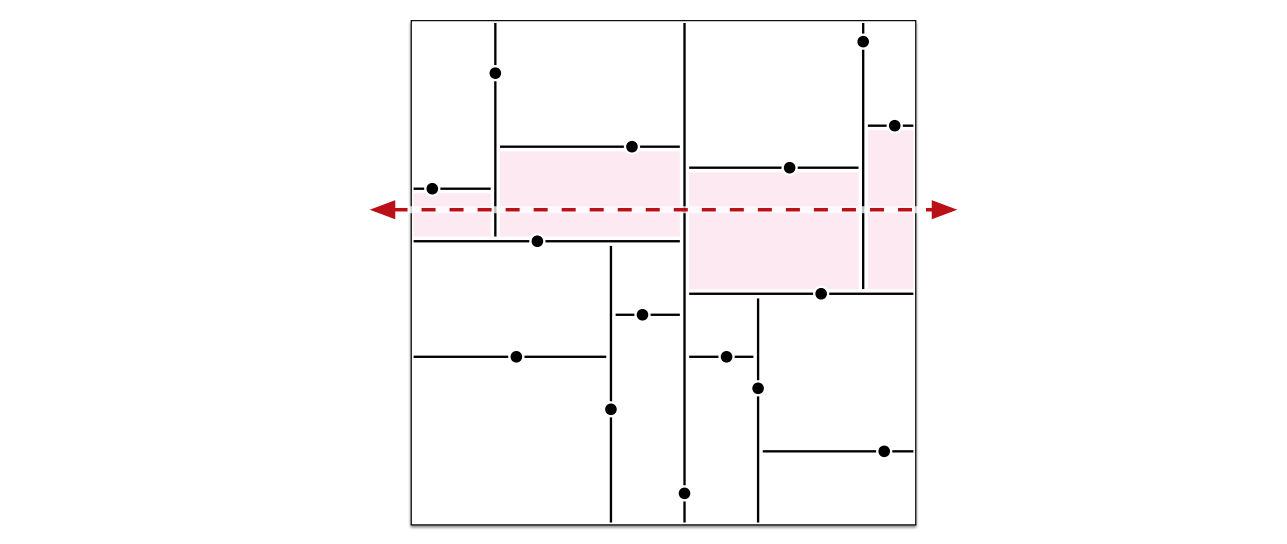図 1.28

15 個の点に対する kd-木、点線は色のついた4つのセルを通る
1. セルの個数を $n$ の関数として求めて、それが正しいことを証明してください。
2. 領域を通過する水平な直線が通るセルの個数の最悪ケースにおける正確な値を $n$ の関数として求めてください。適当な整数 $k$ を使って $n = 2^{k} - 1$ と表せると仮定して構いません。 [ヒント: $f(16) = 4$ となるような関数は二つ以上あります。]
3. kd-木に保存された $n$ 点が与えられたときに、ある水平線よりも上にある点の数をなるべく速く計算するアルゴリズムを説明、解析してください。 [ヒント: (b) を使います。]
4. kd-木に保存された $n$ 点が与えられたときに、垂直および水平な辺からなる長方形 $R$ に含まれる点の数を計算する効率の良いアルゴリズムを説明、解析してください。 [ヒント: (c) を使います。]
❤ CS225 の新入生 Bob Ratenbur は二分木の行きがけ順 (preorder)、通り掛け順 (inorder)、帰りがけ順 (postorder) の走査を行おうとしています。Bob は走査アルゴリズムの基本的な考えをなんとなく理解したのですが、実際に走査を実装するときになって再帰呼び出しをどのように行えばいいかが分からなくなってしまいました。締め切りの 5 分前、Bob は必死になって次のコードを書き上げて提出しました:

procedure $\texttt{PreOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

print $\mathit{label}(v)$

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{left}(v)$)

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{right}(v)$)

procedure $\texttt{InOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{left}(v)$)

print $\mathit{label}(v)$

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{right}(v)$)

procedure $\texttt{PostOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{left}(v)$)

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{right}(v)$)

print $\mathit{label}(v)$

疑似コードの $\blacksquare \blacksquare \blacksquare$ の部分には接頭語 $\textsc{Pre}, {}$$\textsc{In}, {}$$\textsc{Post}$ のどれかが入ります。さらに Bob が提出したコードには次の関数がちょうど一回ずつ含まれています:
- $\textsc{PreOrder}(\mathit{left}(v)), {}$ $\textsc{PreOrder}(\mathit{right}(v))$
- $\textsc{InOrder}(\mathit{left}(v)), {}$ $\textsc{InOrder}(\mathit{right}(v))$
- $\textsc{PostOrder}(\mathit{left}(v)), {}$ $\textsc{PostOrder}(\mathit{right}(v))$
Bob のコードには 36 通りの可能性があります。不幸なことに、Bob は実行可能形式を提出した後に間違ってソースコードを削除してしまいました。そのため彼にもあなたにもどの関数がどこで呼ばれているかは分かりません。

この条件の下で、未知の二分木 $T$ に対して実行された Bob の走査アルゴリズムの出力を配列 $\mathit{Pre}[1..n], \mathit{In}[1..n], \mathit{Post}[1..n]$ に収めることができたとします。これらの配列が一つの二分木 $T$ に対する出力であること、$T$ の頂点ラベルに重複が無いこと、$T$ の葉でない頂点が必ず二つの子を持つことを仮定して構いません。
1. 走査結果から未知の二分木 $T$ を復元するアルゴリズムを説明してください。
2. 走査結果から Bob のコードを復元するか、走査の結果と矛盾しないコードが複数あるので復元できないことを正しく報告するアルゴリズムを説明してください。
例えば、入力 \[ \begin{aligned} \mathit{Pre}[1..n] & = [H A E C B I F G D] \\ \mathit{In}[1..n] & = [A H D C E I F B G] \\ \mathit{Post}[1..n] & = [A E I B F C D G H] \end{aligned} \] に対して、(a) のアルゴリズムは次の木を返します:

(b) のアルゴリズムは次のコードを復元します:

procedure $\texttt{PreOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

print $\mathit{label}(v)$

$\texttt{PreOrder}$($\mathit{left}(v)$)

$\texttt{PostOrder}$($\mathit{right}(v)$)

procedure $\texttt{InOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

$\texttt{PostOrder}$($\mathit{left}(v)$)

print $\mathit{label}(v)$

$\texttt{PreOrder}$($\mathit{right}(v)$)

procedure $\texttt{PostOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

$\texttt{InOrder}$($\mathit{left}(v)$)

$\texttt{InOrder}$($\mathit{right}(v)$)

print $\mathit{label}(v)$
❤ 頂点に数値が保存されている二分木を $T$ とします。 $T$ が二分探索木であるとは (1) $T$ が空である、または (2) $T$ が次の再帰的条件:
- $T$ の左の部分木が二分探索木である。
- 左の部分木にある頂点の値は全て $T$ の根の値より小さい。
- $T$ の右の部分木が二分探索木である。
- 右の部分木にある頂点の値は全て $T$ の根の値より大きい。
を満たすことを言います。

二分木に対する次の二つの操作を考えます:
- 任意の頂点を上に回転 (rotate) させる²⁴。
- 任意の頂点に対して、左右の部分木のスワップ (swap) を行う。
両方の操作において、部分木 $A, B, C$ のいずれかあるいは全てが空でも構いません。
1. $n$ 個の頂点の値に重複がない任意の二分木を受け取って、$O(n^{2})$ 回の rotate と swap でその木を二分探索木に変形させるアルゴリズムを説明してください。五つの頂点を持つ二分木を八回の操作で二分探索木に変形する様子を次に示します。
  
  図 1.29
  
  二分木の「ソート」: rotate 2, rotate 2, swap 3, rotate 3, rotate 4, swap 3, rotate 2, swap 4
  
  答えのアルゴリズムでは親や子のポインタを直接変更したり、新しく頂点を作ったり、元からある頂点を削除することは許されません。木の変更は rotate と swap を使うことでのみ行えます。
  
  一方で木を変更しないなら、何かを計算するのはタダで行えます。アルゴリズムの実行時間は rotate と swap 操作の回数であると定義されているからです。
2. ❤ $n$ 個の頂点を持つ任意の二分木を $O(n \log n)$ 回の rotate と swap で二分探索木に変形するアルゴリズムを説明してください。
3. 任意の二分探索木は $O(n)$ 回の rotate (swap は使わない) で頂点の値が同じ別の二分探索木に変形できることを示してください。
4. ❤ 未解決問題: $n$ 個の頂点を持つ任意の二分木を $O(n)$ 回の rotate と swap で二分探索木に変形するアルゴリズムを示すか、そのようなアルゴリズムは存在しないことを示してください。 [ヒント: 私はこのような変形が可能だとは思いません。]

私が学部生だったときは再帰の妖精ではなく "エルフ" に再帰を任せていました。年を取った靴職人が仕事を終わらせないままベッドに入って翌朝目を覚ますと、エルフ ("Wichtelmänner") が靴を完成させていたというグリム童話に出てくるあのエルフです。私よりも幻覚剤に精通した人なら、この "Rekursionswichtelmänner" のことを Terence McKenna (テレンス・マッケナ) の言葉を借りて「自己改変する機械仕掛けのエルフ (self-transforming machine elves)」と表現するかもしれません。^[return]
Lucas は後に Hanoi の塔を発明したのは 1876 年であったと述べています。^[return]
Lucas は Hanoi の塔を発表するときに N. Claus de Siam (シャムのクロース) という名前を使いました。この名前は "Lucas d'Amiens" (アミアンのリュカ) のアナグラムです。^[return]
この英語訳は W. W. Rouse Ball の 1892 年の著作 Mathematical Recreations and Essays. より。^[return]
"Benares にある大寺院" とはほぼ間違いなくインドのウッタル・プラデーシュ州ヴァーラーナシーにあるカーシー・ヴィシュヴァナート寺院のことです。この寺院は N. Claus という空想上の人物が住んでいるというベトナムのハノイからは 2400 km 西北西にあります。偶然にも、フランス軍がハノイに侵攻したのは 1883 年であり、Lucas が Hanoi の塔パズルを発表したのと同じ年です。この侵攻はフランス領インドシナの首都の成立につながりました。^[return]
Goldstine と von Neumann が提案したのは再帰的でないマージソートであり、現在ではボトムアップマージソートと呼ばれます。当時、大きなデータセットのソートには二進基数ソートの一種を使ってパンチカードを生成する専用用途の機械 ――ほとんどが IBM 製―― が使われていました。EDVAC は IBM の専用用途のソーターよりも速く、さらに "人の仲介や追加の設備を必要とすることなく" ソートができることから、Von Neumann は EDVAC が「汎用 (all purpose)」機械であり、専用用途の機械はもう必要なくなったという (正しい！) 主張をしました。^[return]
Hoare が提案したのはもっと複雑な "双方向" 分割アルゴリズムです。Lomuto のアルゴリズムと比べるとこのアルゴリズムには実用上の利点がある一方で、off-by-one エラーが無限ループを引き起こします。^[return]
一方で、ピボットの添え字 $p$ を一様な乱数によって選んだ場合、$\textsc{QuickSort}$ は全ての入力に対して高い確率で $O(n \log n)$ となります。ここで鍵となるのは乱数がアルゴリズムによって制御されており、コードを読んでから入力を作成する悪意に満ちた全能の攻撃者は制御できない点です。乱数クイックソートの解析は残念ながらこの本の範囲を超えますが、関連する講義ノートを http://algorithms.wtf/ から入手できます。^[return]
数学的に正しく言うと、ここでは $T$ を整数についての関数ではなく実数に対する関数として扱うことでそれ以降の操作を可能にしています。この実数関数に対してある実数 $C \geq 0$ および $n_{0} \geq 0$ があって、全ての $n \leq n_{0}$ で $T(n) = C$ となりますが、この実数の値は重要ではありません。また $n$ が整数のとき $T(n)$ はサイズが $n$ のときのアルゴリズムの実行時間を表しますが、これも議論に関係のないことです。^[return]
実は、ピボットの実用上正しい選び方は一様ランダムに選ぶことです。この方法では中央値を見つけるために必要となる比較演算の回数の期待値が $4n$ となります。詳細は乱数アルゴリズムについての私の講義ノート http://algorithms.wtf を参照してください。^[return]
私の説明は実際に起こったことと少しだけ異なっています。Karatsuba が提案したのは $(a + b)(c + d) - ac - bd = bc + ad$ という等式に基づいたアルゴリズムでした。この場合でも実行時間は $O(n^{\lg 3})$ ですが、再帰方程式が汚くなります。$a - b$ と $c - d$ は $m$ 桁ですが、 $a + b$ と $c + d$ が $m + 1$ 桁となるためです。本文で示した単純化は Donald Knuth (ドナルド・クヌース) によるものです。^[return]
高速フーリエ変換については私の講義ノートがあります: http://algorithms.wtf/^[return]
Schönhage-Strassen のアルゴリズムは 75,000 桁以上の整数に対する実用上最速の乗算アルゴリズムです。Fürer, Harvey, Hoeven らが提案したアルゴリズムが "実用上" 高速となるのは、桁数が宇宙に存在する粒子より大きい整数でだけです。^[return]
De Viribus Quantitatis (『数字の力について』) は初期の娯楽数学に関する重要な著作であり、おそらくは魔法に関する現存最古の著作でもあります。Pacioli は Summa de Arithmetica の著者としての方がよく知られています。これは十五世紀数学のほぼ完全な百科事典であり、複式簿記が説明された最初の書籍です。^[return]
baguenaudier-jeu by EN NOIR & BLANC (CC0 1.0) . 訳注: 英語版とは異なる図を使っています。^[return]
この話には真実が部分的に含まれます。^[return]
最悪ケースにおいて $n$ 個のパンケーキをソートする最適なフリップの正確な値を求める問題は (焼き目の有無に関わらず) 長い間未解決です。できるだけのことをやってみてください。^[return]
4つの要素の中央値は二番目に大きい要素または二番目に小さい要素です。Ke Chen と Adrian Dumitrescu が2014 年に証明したことによると、$k < n / 2$ のときは二番目に小さい要素を、$k > n/2$ のときは二番目に大きい要素を選ぶと、アルゴリズムの実行時間が $O(n)$ となります！詳細は "Select with Groups of 3 or 4 Takes Linear Time" (WADS 2015, arXiv:1409.3600) を見てください。^[return]
Euclid のアルゴリズムが最古の再帰的アルゴリズムである、あるいは最古の自明でないアルゴリズムであると説明されることがありますが、これは間違っています。エジプト人の duplation と mediation を使った乗算アルゴリズムは再帰的であり、自明でもありませんが、Euclid よりも少なくとも 1500 年前に使われています。^[return]
Euclid はこれを示していません。『原論』の第四巻の命題 1 は「$\textsc{EuclidGCD}(x,y) = 1$ ならば $x$ と $y$ は互いに素 ($\gcd (x, y) = 1$)」ですが、その証明は $x \text{ mod } (y \text{ mod } (x \text{ mod } y))= 1$ という特殊な場合しか考えていません。また命題 2 は「$x$ と $y$ が互いに素でないならば $\textsc{EuclidGCD}(x, y) = \gcd (x, y)$」ですが、その証明は $\gcd (x, y) = y$ と $\gcd (x, y) = y \text{ mod } (x \text{ mod } y)$ という場合しか考えていません。さらに言えば、この二つの命題が正しくても $\textsc{EuclidGCD}$ の正しさは証明できません。Euclid のようにならないでください。^[return]
現実の政治はもっと複雑ですが、これは理論の本です！^[return]
訳注: 英語版ではこの後に画像がありますが、権利の都合でコピーできませんでした。^[return]
スリル満点の最終章 Retcon the Squirrel では、最後まで生き残ったヒーローがタイムトラベルして事前に $n - 1$ 人のヒーローを本物そっくりの風船人形に入れ替えることでヒーロー全員を救います。えぇ、そうです。これが Avengers: Endgame のあらすじです。^[return]
rotate は二分木の行きがけ順を保存します。そのため二分探索木の中にはバランスを保つのに rotate 操作を使うものがあります。例えば AVL 木、赤黒木、スプレー木、スケープゴート木、treap などです。これらのデータ構造は http://algorithms.wtf にある講義ノートで解説されています。^[return]