最良優先: Dijkstra のアルゴリズム

幅優先探索では FIFO を使っていましたが、この FIFO を頂点 \(v\) に対する鍵が暫定的な距離 \(\mathit{dist}(v)\) であるような優先度付きキューで置き換えると、別の最短路アルゴリズムが手に入ります。1957 年にこのアルゴリズムを初めて "出版" したのは Michael Leyzorek (マイケル・レイゾレク) を中心とするケース工科大学の研究者チームで、米陸軍電子機器性能証明実験場の戦闘開発部署に対する定期報告書でのことでした。同じアルゴリズムは Edsger Dijkstra (エドガー・ダイクストラ) によって 1956 年に独立に発見され (1959 年に出版され)、1960 年には George Minty (ジョージ・ミンティ) によって、同じく 1960 年には P.D. Whiting (P・D・ホワイティング) と J.A. Hillier (J・A・ヒラー) によっても独立に発見されています。また 1958 年には George Dantzig (ジョージ・ダンツィグ) がほとんど同じアルゴリズムを示しています。古い文献ではこのアルゴリズムが "Minty のアルゴリズム" と呼ばれることもありますが、現在では世界中で "Dijkstra のアルゴリズム" と呼ばれており、スティグラーの法則に完全に従っています¹。Dijkstra のアルゴリズムの疑似コードを次に示します:

procedure \(\texttt{Dijkstra}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

\(\texttt{Insert}\)(\(s, 0\))

while 優先度付きキューが空でない do

\(u \leftarrow \)\(\texttt{ExtractMin}\)()

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

if \(v\) が優先度付きキューにある then

\(\texttt{DecreaseKey}\)(\(v, \mathit{dist}(v)\))

else

\(\texttt{Insert}\)(\(v, \mathit{dist}(v)\))

簡単な帰納法によって、アルゴリズムの実行中に \(u \rightarrow v\) が緊張しているのは頂点 \(u\) が優先度付きキューにあるときか、そうでなければ \(u\) を優先度付きキューから \(\textsc{ExtractMin}\) したときであることが示せます。よって Dijkstra のアルゴリズムが Ford の一般的な戦略のインスタンスであり、したがって \(G\) に負閉路が含まれない場合には最短路を正しく計算することが分かります。

負辺無し

Dijkstra のアルゴリズムはグラフに負辺が含まれないときにとても解析しやすい動作をします。この設定ではアルゴリズムによって作られる波面がソース頂点 \(s\) からの距離が大きくなる順番で広がっていくので、動作は幅優先探索と似ています。実行の様子を次の図に示します:

図 8.12

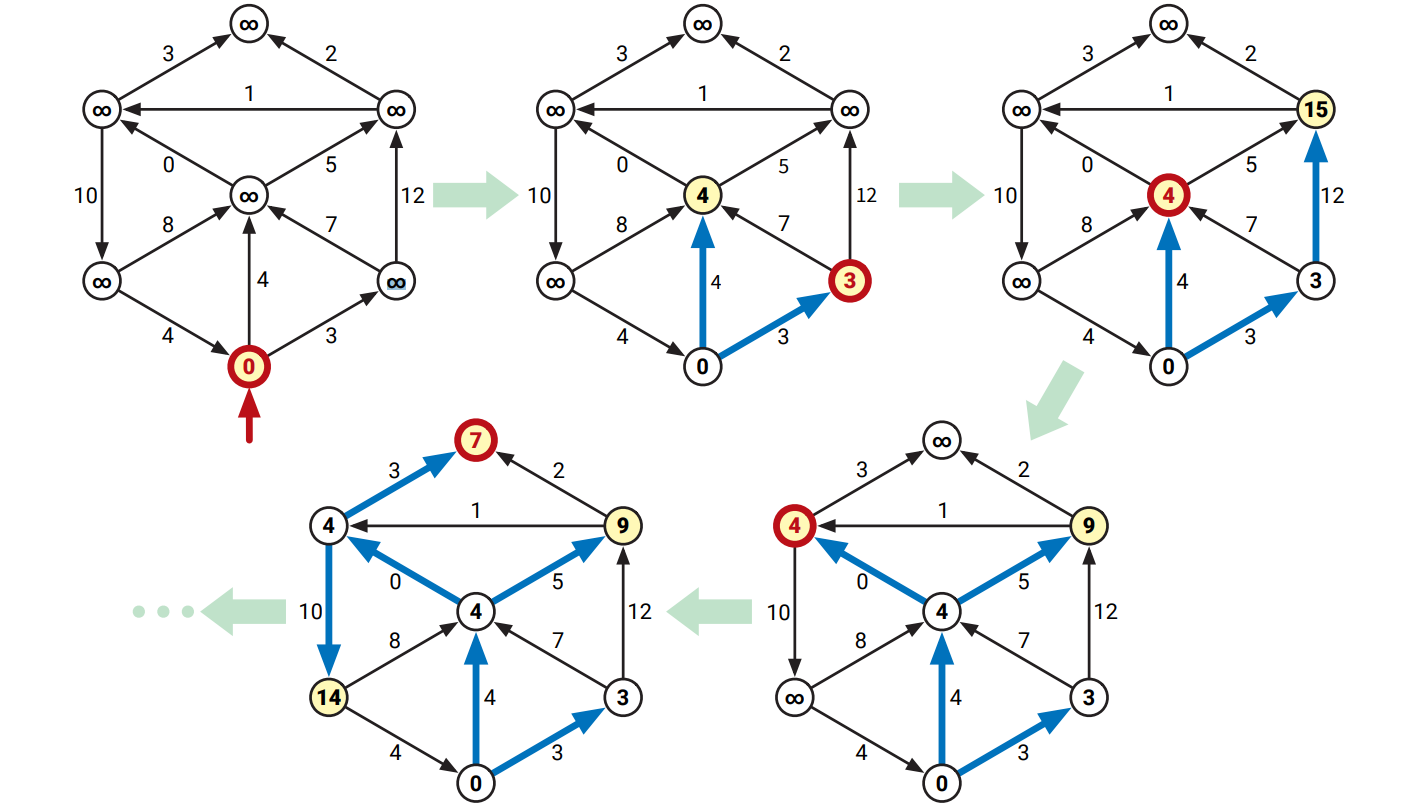
負辺を持たないグラフに対して Dijkstra のアルゴリズムを実行したときの最初の四反復。各反復において、青くて太い辺が前者からの辺を、黄色い頂点が優先度付きキューにある頂点を、太字の赤い頂点が次にスキャンされることを表す。

波面の比喩をたどっていけば、この設定の下での Dijkstra のアルゴリズムの正しさの直接的な証明ができます。任意の整数 \(i\) に対して、\(i\) 番目の \(\textsc{ExtractMin}\) が返す頂点を \(u_{i}\) と表し、この \(\textsc{ExtractMin}\) の直後の \(\mathit{dist}(u_{i})\) の値を \(d_{i}\) で表すことにします。例えば \(u_{1} = s\) および \(d_{1} = 0\) です。同じ頂点が複数回 \(\textsc{ExtractMin}\) される可能性があるので、まだこの時点では \(u_{i}\) が全て異なるとは仮定できません。

命題 8.3 \(G\) に負辺が無いならば、任意の整数 \(i < j\) について \(d_{i} \leq d_{j}\) が成り立つ。

証明 \(G\) に負辺が含まれないとし、\(i\) を適当な添え字とする。\(d_{i+1} \geq d_{i}\) を示せば十分であり、考える場合は二つある。

メインループの \(i\) 番目のループで辺 \(u_{i} \rightarrow u_{i+1}\) が緩和される場合。このとき \(i\) 番目の反復の終了時には \(\mathit{dist}(u_{i+1}) = \mathit{dist}(u_{i}) + w(u_{i} \rightarrow w_{i+1})\) であり、負辺が存在しないことから \(\mathit{dist}(u_{i+1}) \geq \mathit{dist}(u_{i})\) が成り立つ。
メインループの \(i\) 番目のループで辺 \(u_{i} \rightarrow u_{i+1}\) が緩和されないか、辺 \(u_{i} \rightarrow u_{i+1}\) が存在しない場合。このとき \(i\) 番目の反復の開始時点で \(u_{i+1}\) が優先度付きキューにあり、反復の最初の \(\textsc{ExtractMin}\) で \(u_{i}\) が帰っていることから \(\mathit{dist}(u_{i+1}) \geq \mathit{dist}(u_{i})\) である。さらに \(i\) 番目の反復で \(\mathit{dist}(u_{i+1})\) の値は変化しないので、 \(\mathit{dist}(u_{i+1}) \geq \mathit{dist}(u_{i})\) が成り立つ。

どちらの場合においても \(d_{i+1} \geq d_{i}\) であり、簡単な帰納法から示したい命題が示せる。 \(\Box\)

命題 8.4 \(G\) に負辺が無いならば、\(G\) の任意の頂点は最大でも一度だけ優先度付きキューから \(\textsc{ExtractMin}\) される。

証明背理法で示す。\(v\) が二度以上 \(\textsc{ExtractMin}\) されるとする。具体的には、\(v\) が \(i\) 番目の反復で \(\textsc{ExtractMin}\) され、\(j\) 番目の反復で \(\textsc{Insert}\) され、\(k\) 番目の反復でもう一度 \(\textsc{ExtractMin}\) されるとする (\(i < j < k\))。一つ前の命題の記法を使うと、\(v = u_{i} = u_{k}\) である。

距離のラベル \(\mathit{dist}(v)\) は増加せず、\(\mathit{dist}(v)\) は \(j\) 番目の反復で \(\textsc{Insert}\) される前に狭義に減少するので、\(d_{i} > d_{k}\) である。よって一つ前の命題より、\(G\) には少なくとも一つの負辺が含まれることになるが、これは問題の仮定と矛盾する。 \(\Box\)

命題 8.4 から全ての頂点が最大でも一度だけスキャンされ、全ての辺が最大でも一回だけ緩和されることが分かります。しかし幅優先探索と違って、距離のラベル \(\mathit{dist}(v)\) は複数回書き換えられます。最初に \(\mathit{dist}(v)\) が書き換えられるのは \(\mathit{dist}(v) = \infty\) から値が変わるときで、その直後 \(v\) は優先度付きキューに \(\textsc{Insert}\) され、その後は \(\textsc{DecreaseKey}\) によって \(\mathit{dist}(v)\) が変更されます。一度 \(v\) が \(\textsc{ExtractMin}\) されれば、それ以降 \(v\) の距離のラベルは変化しません。

正しさの証明の残りの部分は幅優先探索のものとほとんど同じです。

定理 8.5 \(G\) に負辺が無いならば、\(\textsc{Dijkstra}(s)\) が停止したとき、任意の頂点 \(v\) に対して \(\mathit{dist}(v)\) は \(s\) から \(v\) への最短路の長さと等しい。

証明 \(v\) を任意の頂点とし、任意の路 \(s = v_{0} \rightarrow\) \(v_{1} \rightarrow\) \(\cdots \rightarrow\) \(v_{l} = v\) を考える。任意の添え字 \(j\) に対して、部分路 \(v_{0} \rightarrow\) \(v_{1} \rightarrow\) \(\cdots \rightarrow v_{j}\) の長さを \(L_{j}\) とする。任意の \(j\) について\(\mathit{dist}(v_{j}) \leq L_{j}\) を帰納法で示す。

\(\mathit{dist}(v_{0}) = \mathit{dist}(s) = 0 = L_{0}\) は明らか。
\(j > 0\) を任意の整数とする。帰納法の仮定から \(\mathit{dist}(v_{j-1}) \leq L_{j-1}\) であり、優先度付きキューから \(v_{j-1}\) を \(\textsc{Pull}\) したとき \(\mathit{dist}(v_{i}) \leq \mathit{dist}(v_{j-1}) + w(v_{j-1} \rightarrow v_{j})\) が最初から成り立っているか、そうでなければ \(\mathit{dist}(v_{i}) \leftarrow \mathit{dist}(v_{j-1}) + w(v_{j-1} \rightarrow v_{j})\) という代入が行われる。よって \[ \mathit{dist}(v_{j}) \leq \mathit{dist}(v_{j-1}) + w(v_{j-1} \rightarrow v_{j}) \leq L_{j-1} + w(v_{j-1} \rightarrow v_{j}) = L_{j} \] が成り立つ。

\(\mathit{dist}(v)\) が最大でも \(s\) から \(v\) への任意の路の長さにしかならないことが示せたので、\(\mathit{dist}(v)\) は \(s\) から \(v\) への最短路の長さである。

同様の帰納法によって \(\mathit{dist}(v)\) が前者をたどった路 \(s \rightarrow\) \(\cdots \rightarrow\) \(\mathit{pred}(\mathit{pred}(v)) \rightarrow\) \(\mathit{pred}(v) \rightarrow v\) の長さと等しいことが分かるので、この路が最小路である。 \(\Box\)

最後に Dijkstra のアルゴリズムの実行時間を調べます。\(\textsc{Dijkstra}\) は最大で \(E\) 回の \(\textsc{DecreaseKey}\) と \(V\) 回の \(\textsc{Insert}\) と \(V\) 回の \(\textsc{ExtractMin}\) を行います。標準的な二分ヒープを使うとこれらの操作は全て \(O(\log V)\) 時間で行えるので、アルゴリズム全体の実行時間は \(\pmb{O(E\log V)}\) です²。

グラフに負辺が無いことが事前にわかっているなら、Dijkstra のアルゴリズムを単純にできます。具体的には、初期化処理において優先度付きキューに全ての頂点を入れておき、メインループでは \(\textsc{DecreaseKey}\) だけを呼びます。ほとんどのアルゴリズムの教科書で紹介されているのはこのバージョンの Dijkstra のアルゴリズムであり、Wikipedia および Dijkstra の原著論文に載っているのもこのバージョンです。また五章で説明した "最良優先探索" もこの形をしていました。

procedure \(\texttt{NonNegativeDijkstra}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

for 頂点 \(v\) do

\(\texttt{Insert}\)(\(\color{red}{v, \mathit{dist}(v)}\))

while 優先度付きキューが空でない do

\(u \leftarrow \)\(\texttt{ExtractMin}\)()

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

\(\texttt{DecreaseKey}\)(\(\color{red}{v, \mathit{dist}(v)}\))

図 8.13

負辺が無いグラフだけを扱える単純化された Dijkstra のアルゴリズム (\(\textsc{Dijkstra}\) からの変化が赤で示されている)

❤ 負辺あり

グラフに負辺が含まれる場合、\(\textsc{NonNegativeDijkstra}\) は最短路を正しく計算できません。また辺の重みが全て正だったとしても、 \(\textsc{NonNegativeDijkstra}\) は (理論上も、実際のプログラムでも) \(\textsc{Dijkstra}\) より高速なわけではありません。このことから、\(\textsc{NonNegativeDijkstra}\) ではなくて \(\textsc{Dijkstra}\) こそが "Dijkstra のアルゴリズム" と呼ぶにふさわしいアルゴリズムであると私は考えています。Edsger Dijkstra がかつて言ったように、「たまに遅くなる正しいアルゴリズムは、たまに間違う速いアルゴリズムよりも優れている」からです！それに、遅くなると言っても実際はほとんど遅くなりません。

グラフが負辺を持つ場合には、これまで使ってきた "波面を広げる" という比喩は残念なことに使えなくなります。同じ頂点が複数回 \(\textsc{ExtractMin}\) されることがあり、同じ辺が複数回緩和されることもあり、また各頂点の距離のラベルが常に大きくなるとは限りません。次の図に示す例では左上の頂点が六回 \(\textsc{ExtractMin}\) されており、上の辺は全て二回ずつ緩和されています。

図 8.15

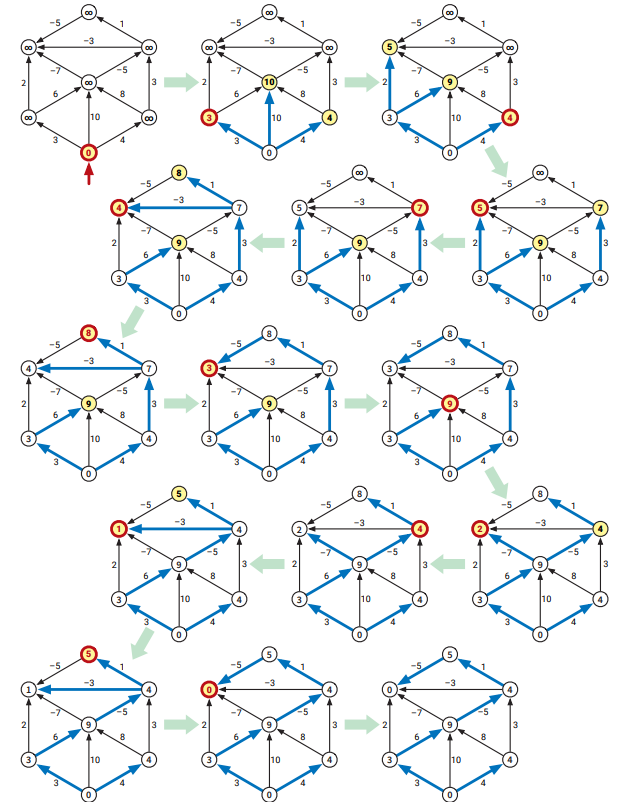
負辺を持ったグラフに対する Dijkstra のアルゴリズムの完全な実行例。各反復において、青くて太い辺が前者へのポインタを、黄色い頂点が優先度付きキューにある頂点を、赤い太字の頂点が次にスキャンする頂点を表す。図 8.16 と比較すること。

実は、負閉路が含まれないこと以外の制約が無いグラフに対する \(\textsc{Dijkstra}\) の最悪計算時間は指数的になります。次に示すグラフは \(\textsc{Dijkstra}\) が \(\Theta(2^{V/2})\) 回の緩和を行う (Douglas Shier と Christoph Witzgall によって発見された) グラフのクラスです³。\(\Theta(2^{V})\) 回の緩和が行われるさらに複雑なグラフの族もあります (練習問題とします)。しかし現実のグラフに対しては、負辺があったとしても Dijkstra のアルゴリズムはたいてい高速に実行できます。

図 8.14

\(\textsc{Dijkstra}\) の実行時間が指数時間となる、負辺を持った有向グラフ

歴史的に不正確なのは承知で、私はこの慣習に従います。 "Leyzorek-Gray-Johnson-Ladew-Meaker-Petry-SeitzDantzig-Dijkstra-Minty-Whiting-Hillier のアルゴリズム" と書かれているのを読みたい人はいないでしょうし、実際に出版されなかった論文というのは発見とみなされないからです。^[return]
1950 年代の最短路に関する論文は優先度付きキューに全く言及していません。Dijkstra が提案したのは一番外側の波面にある全ての頂点を各反復で総当たりで調べる方法です。このアルゴリズムの実行時間は \(\pmb{O(V^{2})}\) であり、\(E = \Omega(V^{2})\) の場合には二分ヒープを使った実装よりも高速です！Minty が提案したのは辺 \(u \rightarrow v\) であって \(\mathit{dist}(u)\) が有限かつ \(\mathit{dist}(v)\) が無限のものに対する総当たりであり、この場合の実行時間は \(O(VE)\) です。二分ヒープとして実装された優先度付きキューを使ったほぼ線形の実行時間を最初に示したのは Donald Johnson (ドナルド・ジョンソン) で、1977 年のことです。フィボナッチヒープと呼ばれるさらに複雑な優先度付きキューのデータ構造を使えば実行時間を \(\pmb{O(E+ V \log V)}\) まで改善できます。またさらに洗練された優先度付きキューを使えば、辺の重みが特殊な場合に対する高速なアルゴリズムを作ることができます。^[return]
面白いことに、Shier と Witzgall の例は辺が \(O(V)\) 個しか含まれない DAG です。よって仮にジグザグな路が最短路木であることを知らなかったとしても、最短路は (他の最短路アルゴリズムを使って) \(O(V)\) 時間で計算できてしまいます。^[return]