有向非巡回グラフ: 深さ優先探索
有向非巡回グラフの最小路を計算するのは簡単であり、辺に重みが付いていても、その重みが負であったとしても簡単です (負閉路を気にする必要ありません。定義により、閉路が無いのですから!)。実はこれは完全に標準的な動的計画法のアルゴリズムです。
\(G\) を辺に重みの付いた有向非巡回グラフ、\(s\) を固定された開始頂点とします。任意の頂点 \(v\) に対して、\(\mathit{dist}(v)\) で \(G\) における \(s\) から \(v\) への最短路の長さを表すことにします。するとこの関数は次の単純な再帰方程式を満たします: \[ \mathit{dist}(v) = \begin{cases} 0 & \text{if } v = s \\ \min\limits_{u \rightarrow v} (\mathit{dist}(u) + w(u \rightarrow v)) & \text{それ以外} \end{cases} \] 実は、この等式は全ての有向グラフについて成り立ちます。しかしこの式が再帰方程式として定義されるのは有向非巡回グラフに対してだけです (入力グラフ \(G\) が閉路を持っているとき、この関数は無限ループに入ってしまうため)。\(G\) が DAG ならば、全ての再帰的な呼び出しはトポロジカル順序で前にある頂点を訪れるだけで必ず評価できます。こうして出来上がるアルゴリズムを次に示します:
procedure \(\texttt{DagSSSP}\)(\(s\))
for トポロジカル順序の頂点 \(v\) do
if \(v = s\) then
\(\mathit{dist}(v) \leftarrow 0\)
else
\(\mathit{dist}(v) \leftarrow \infty\)
for \(u \rightarrow v\) の形をした辺 do
if \(\mathit{dist}(v) > \mathit{dist}(u) + w(u \rightarrow v)\) then
⟨⟨緊張している辺 \(u \rightarrow v\) を緩和する⟩⟩
\(\mathit{dist}(v) \rightarrow \mathit{dist}(u) + w(u \rightarrow v)\)
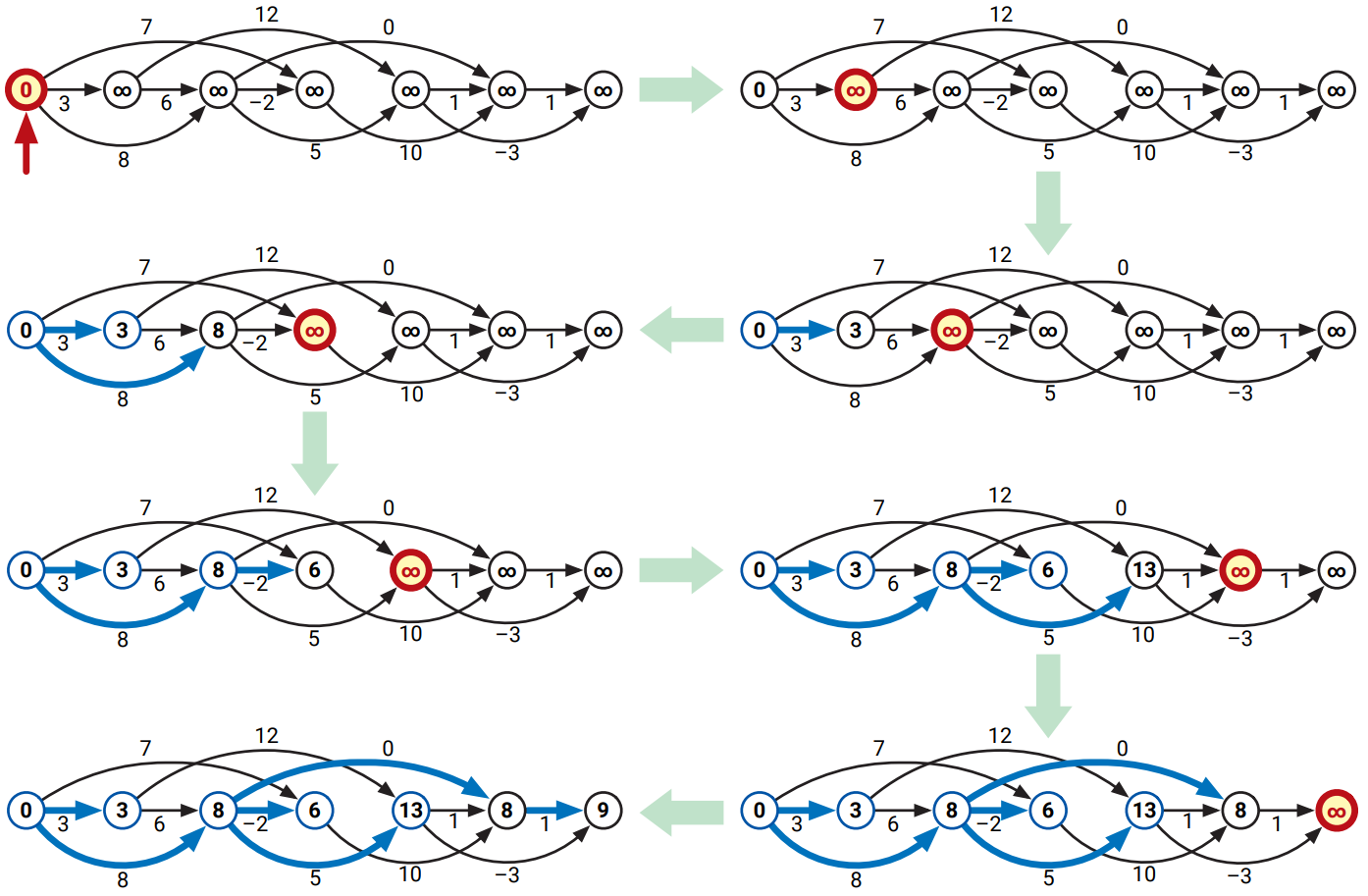
\(\mathit{dist}\) の再帰方程式の依存グラフは入力グラフ \(G\) の逆グラフです: 小問題 \(\mathit{dist}(v)\) が \(\mathit{dist}(u)\) に依存するのは \(G\) に辺 \(u \rightarrow v\) があるときだけだからです。よって \(G\) の逆に対する深さ優先探索を行って頂点を帰りがけ順に考えることで、各頂点に対する最短路の長さを \(\pmb{O(V+E)}\) 時間で計算できます。同じことですが、\(G\) のトポロジカル順序で頂点を考えるとも言えます。
この動的計画法のアルゴリズムはFord の一般的な緩和アルゴリズムのもう一つの例でもあります! \(\mathit{dist}(v)\) の初期化をメインループの外に出し、前者へのポインタを追加する処理を加えるとこの関係がより明確になります。このアルゴリズムを次に示します:
procedure \(\texttt{DagSSSP}\)(\(s\))
\(\texttt{InitSSSP}\)(\(s\))
for トポロジカル順序の頂点 \(v\) do
for \(u \rightarrow v\) の形をした辺 do
if \(u \rightarrow v\) が緊張している then
\(\texttt{Relax}\)(\(u \rightarrow v\))
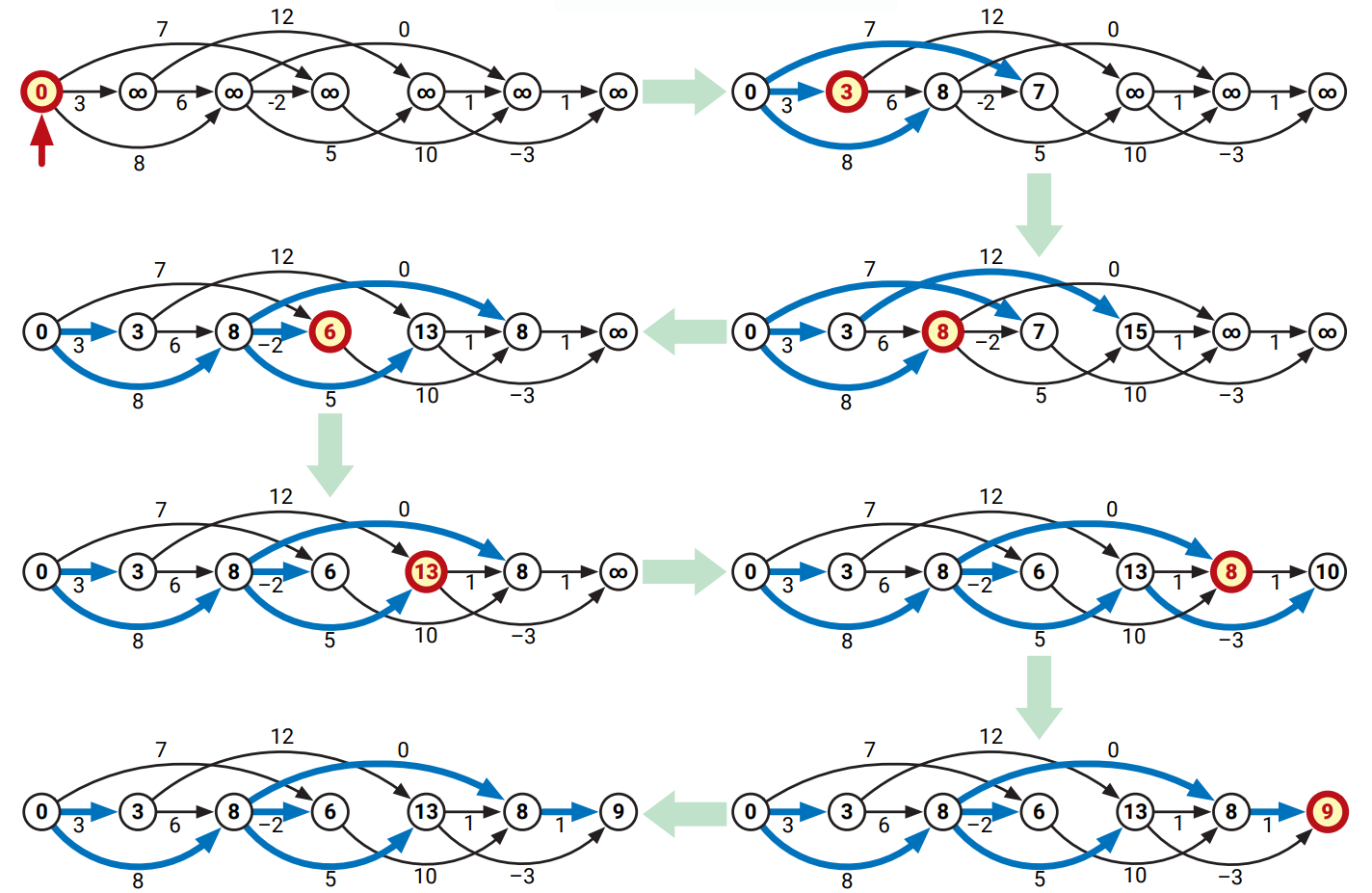
幅優先探索や Ford の緩和戦略の他のインスタンスと比べると、\(\textsc{DagSSSP}\) には少しだけ違いがあります。他の最短路アルゴリズムが頂点を調べるときは頂点から出る辺を緩和させようとするので、直感的には波面を外側に向かって押し広げるような処理をします。これに対して \(\textsc{DagSSSP}\) では頂点に向かう辺を緩和させようとするので、直感的には波面をこちら側に引っ張るような処理をします。
ただし、やってくる辺ではなく外側に向かう辺を考えるように \(\textsc{DagSSSP}\) を改変することは可能です。このすると他の最短路アルゴリズムに良く似た、 DAG の最短路を \(\pmb{O(V + E)}\) 時間で計算する別のアルゴリズムが手に入ります:
procedure \(\texttt{PushDagSSSP}\)(\(s\))
\(\texttt{InitSSSP}\)(\(s\))
for トポロジカル順序の頂点 \(\color{red}{u}\) do
for \(u \rightarrow v\) の形をした辺 do
if \(u \rightarrow v\) が緊張している then
\(\texttt{Relax}\)(\(u \rightarrow v\))
このアルゴリズムを前図と同じグラフに対して実行した様子を次の図に示します。\(\textsc{PushDagSSSP}\) の正しさは Ford の一般的な緩和戦略の正しさから従いますが、頂点のトポロジカル順序に関する帰納法を使って直接示すのも難しくありません。