練習問題
-
辺に任意の重みが付いた、負閉路が含まれないとは限らない有向グラフを \(G\) とし、\(s\) を \(G\) の適当な頂点とします。
-
全ての頂点 \(v\) が \(\mathit{dist}(v)\) を保持しているとします (前者へのポインタは保持していません)。このとき全ての \(v\) について \(\mathit{dist}(v)\) が \(s\) から \(v\) への最短路の長さかどうかを判定するアルゴリズムを説明、解析してください。
-
全ての頂点 \(v \neq s\) が \(G\) の他の頂点へのポインタ \(\mathit{pred}(v)\) を保持しているとします (距離は保持していまません)。このとき前者へのポインタ全体が \(s\) を根とする単一ソース最短路木を定義するかどうかを判定するアルゴリズムを説明、解析してください。
-
-
ループ木 (looped tree) とは、木に葉から根に向かう辺を追加してできる重み付きの有向グラフのことを言います。辺の重みは非負とします。
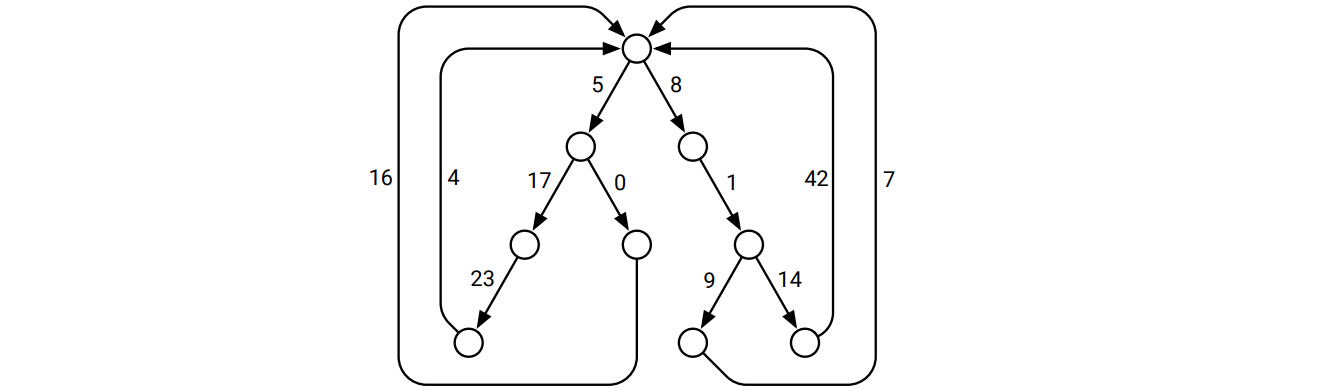 ループ木
ループ木-
\(n\) 個の頂点を持つループ木に対して、Dijkstra のアルゴリズムを使って二つの頂点 \(u\) と \(v\) の間の最短路を計算するとどれくらいの時間がかかりますか?
-
Dijkstra のアルゴリズムよりも高速なアルゴリズムを説明、解析してください。
-
-
辺に重みの付いた有向グラフ \(G\) と二つの頂点 \(s, t\) が与えられたとします。
-
\(G\) がちょうど一つの負辺を持つときに、\(s\) から \(t\) への最短路を計算するアルゴリズムを説明、解析してください。 [ヒント: Dijkstra のアルゴリズムを変更するか、あるいは変更しないでください。]
-
\(G\) がちょうど \(k\) 個の負辺を持つときに、\(s\) から \(t\) への最短路を計算するアルゴリズムを説明、解析してください。アルゴリズムの実行時間は \(k\) にどのように依存しますか?
-
-
全ての頂点に正の重みが付いた無向グラフ \(G\) が与えられたとします。
-
\(G\) の全域木で重みが最小のものを見つけるアルゴリズムを説明、解析してください (全域木の重みとは含まれる頂点の重みの和です)。
-
二つの頂点 \(s, t\) が与えられたときに、\(s\) から \(t\) への路で重みが最小のものを見つけるアルゴリズムを説明、解析してください (路の重みとは含まれる頂点の重みの和です)。
[ヒント: 片方の問題の答えは自明です。]
-
-
グラフ \(G\) とその辺 \(e\) に対して、\(G \backslash e\) で \(G\) から \(e\) を削除して得られるグラフを表すことにします。置換路問題 (replacement paths problem) とは、グラフ \(G\) と二つの頂点 \(s, t\) が与えられたときに、全ての辺 \(e\) に対して \(G \backslash e\) における \(s\) から \(t\) への最短路を計算する問題です。問題の答えは最短路の長さを収めた配列 \(E\) であり、\(E\) の添え字が取り除く \(G\) の辺に対応します。
-
\(G\) が有向グラフであり、\(G\) における \(s\) から \(t\) への最短路が \(G\) の全ての頂点を訪れるとします。この特殊ケースに対する置換路問題を \(O(E\log V)\) 時間で解くアルゴリズムを説明してください。
-
❤ 任意の無向グラフに対する置換問題を \(O(E\log V)\) 時間で解くアルゴリズムを説明してください。
両方の問題において、辺の重みは非負であると仮定してください。 [ヒント: \(G\) における最短路の辺を削除した場合、元の最短路と新しい最短路はどのように重なりますか?]
-
-
\(G = (V, E)\) を辺に非負の重みが付いた有向グラフ、\(s, t\) を \(G\) の頂点、\(H\) を \(G\) からいくつかの辺を削除して得られるグラフとします。\(G\) から取り除いた辺を一つだけ \(H\) に戻して \(s\) から \(t\) への最短路の長さを最短にしたいとしたとき、戻すべき辺を \(O(E \log V)\) 時間で選択するアルゴリズムを説明、解析してください。
-
-
Bellman-Ford のアルゴリズムを改変して、 \(s\) から到達可能な負閉路がある場合にはその負閉路を返し、そのような負閉路が無い場合には最短路木を返すアルゴリズムを作ってください。またそのアルゴリズムの解析も行ってください。改変されたアルゴリズムの実行時間は \(O(VE)\) のままであるべきです。
-
Bellman-Ford のアルゴリズムを改変して、入力グラフに負閉路が含まれている場合でも \(s\) から他の全ての頂点への最短路を正しく計算するアルゴリズムを作ってください。つまり、アルゴリズムは \(s\) から \(v\) への負閉路を含む歩道が存在するなら \(\mathit{dist}(v) = -\infty\) とし、そうでないなら \(s\) から \(v\) への最短路の長さを \(\mathit{dist}(v)\) に代入します。アルゴリズムの解析も行ってください。改変されたアルゴリズムの実行時間は \(O(VE)\) のままであるべきです。
-
❤ (a) と (b) を Ford の一般的な緩和アルゴリズムに対して解いてください。改変されていない Ford のアルゴリズムが負辺を含まないグラフに対しては \(O(2^{V})\) ステップで停止することを既知として構いません。改変されたアルゴリズムの実行時間も \(O(2^{V})\) であるべきです。
-
-
次に示す、さらに意味の曖昧な Ford の一般的な緩和アルゴリズムの変種を考えます:
procedure \(\texttt{FellmannBored}\)(\(s\))
\(\texttt{InitSSSP}\)(\(s\))
while 飽きるまで do
\(e_{i} \leftarrow G\) の適当な辺
if \(e_{i}\) が緊張している then
\(\texttt{Relax}\)(\(e_{i}\))
\(s\) を始点とする適当な歩道 \(W\) の辺を順番にチェックしていった場合、\(W\) の最後の辺につけられる距離のラベルは \(W\) の長さ以下であることを示してください。きちんと言うと: 任意の歩道 \(s = v_{0} \rightarrow v_{1} \rightarrow \cdots \rightarrow v_{l}\) について、辺をこの順番で調べていったときに \(\mathit{dist}(v_{l}) \leq \sum_{i=1}^{l} w(v_{i-1} \rightarrow v_{i})\) であることを示してください。 [ヒント: この命題を証明することは正しく主張することよりも簡単なぐらいです。]
-
この問題では Ford の一般的な緩和アルゴリズムを使って負閉路を検出する方法について考えます。
-
\(\mathit{pred}(s)\) が \(\textsc{InitSSSP}\) の後に一度でも変更されるならば、入力グラフに \(s\) を通る負閉路が含まれることを示してください。
-
入力グラフに \(s\) を通る負閉路が含まれていたとしても \(\mathit{pred}(s)\) が \(\textsc{InitSSSP}\) の後に一度も変更されない場合があることを示してください。
-
前者への辺 \(\mathit{pred}(v) \rightarrow v\) の集合からなるグラフを \(P\) とし、緊張している辺の集合を \(X\) とします。\(P\) と \(X\) はどちらもアルゴリズムの実行が進むにつれて変化します。グラフが閉路を含まないのは \(P \cup X\) が常に DAG である場合に限ることを示してください。
-
これまでに緩和された辺の集合を \(R\) とします。\(R\) はアルゴリズムの実行が進むにつれて変化します。グラフが閉路を含まないのは \(R\) が常に DAG である場合に限ることを示してください。
-
-
❤ 辺の重みが負でもあり得る場合、DAG に対する Dijkstra のアルゴリズムが最悪ケースで \(\Theta(2^{V})\) 回の緩和を行うことを示してください。具体的には、任意の正の整数 \(n\) に対して、Dijkstra のアルゴリズムが \(\textsc{Relax}\) を \(\Theta(2^{n})\) 回呼ぶ \(n\) 頂点の重み付きDAG \(G_{n}\) を構築してください。 [ヒント: バイナリカウンタ]
-
❤ 入力グラフが負閉路を持たないならば、Ford の一般的な緩和アルゴリズムが (したがって Dijkstra のアルゴリズムも) 最大でも \(O(2^{V})\) 回の緩和の後に停止することを示してください。 [ヒント: 問題 9.9.(d)]
-
有向グラフ \(G\) が与えらたとします。\(G\) はソース \(s\) を持っていて、さらに全ての辺に負の重み ("長さ") が付いているとします。このとき \(s\) から他の全ての頂点への最短経路の長さを計算する効率の良いアルゴリズムを説明、解析してください。つまり、全ての頂点 \(t\) に対して次の仕様を満たすアルゴリズムを説明してください:
-
\(t\) に \(s\) から到達できないなら、アルゴリズムは \(\mathit{dist}(t) = \infty\) を出力する。
-
\(G\) が \(s\) から到達できる閉路を持ち、その閉路から \(t\) に到達である場合、\(s\) から \(t\) への路 (正しくは歩道) の長さは任意に小さな負の値を取れるので、最短経路の距離が定義できなくなる。この場合のアルゴリズムは \(\mathit{dist}(t) = -\infty\) を出力する。
-
二つのどちらでもない場合、アルゴリズムの出力は \(s\) から \(t\) への最短経路の長さを正しく出力する。
-
-
これまで考えてきたのは二つの頂点の間の "唯一の" 最短路 ("the" shortest path) でしたが、一つグラフの中に同じ頂点を結ぶ最短路が複数あることがあります。そのような場合、重み付きグラフに対する問題であっても、重みが最小の路の中で辺の一番少ないものを選ぶのが望ましいことが多いです。このような路を \(s\) から \(t\) への最良路 (best path) と言います。辺に正の重みが付いた有向グラフ \(G\) とソース頂点 \(s\) が与えられたとします。\(G\) における \(s\) から他の頂点への最良路を計算するアルゴリズムを説明、解析してください。
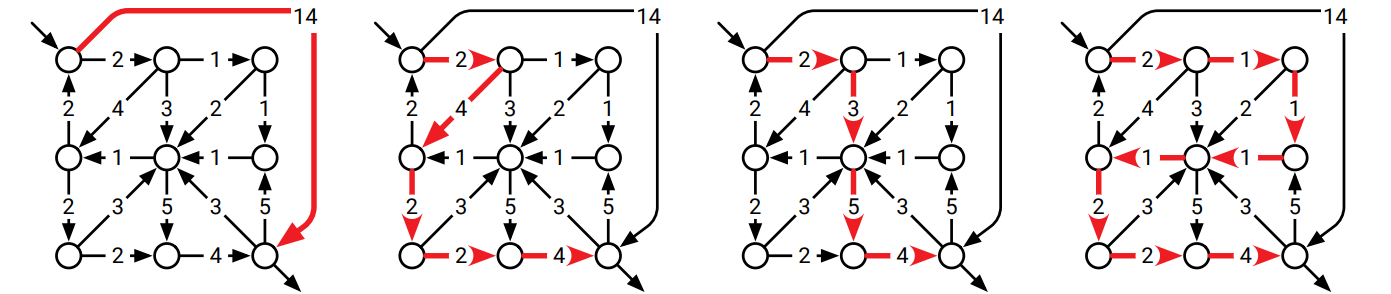 図 8.18長さの等しい四つの最短路 (最短路は他にもある)。一番左の路が「最良」の最短路である。
図 8.18長さの等しい四つの最短路 (最短路は他にもある)。一番左の路が「最良」の最短路である。 -
辺に重みの付いた有向グラフ \(G\) において、頂点 \(s\) から頂点 \(t\) への最短路の数を計算するアルゴリズムを説明、解析してください。辺の重みは正であり、算術演算は \(O(1)\) で行えると仮定して構いません。 [ヒント: \(s\) から他の全ての頂点に対する最短路の長さを計算し、\(s\) から他の頂点への最短路に含まれない辺を全て取り除きます。何が残りますか?]
-
あなたは小学校時代の親友を Twitbook で見つけました。あなたも相手もすぐにでも会いたいと思っているのですが、二人は遠くは離れた都市に住んでいます。旅行の時間を最小化するために、二人はお互いの住む都市の中間にある都市で会うことにしました。二人はそう決めてすぐに車に乗り込みましたが、さて、正確にどこで会えばよいのでしょうか?
重み付きグラフ \(G=(V,E)\) が与えられ、頂点 \(V\) が都市を、辺 \(E\) が都市の間を結ぶ道路を表します。全ての辺 \(e\) には重み \(w(e)\) が付いており、二つの都市の間を車で移動するのにかかる時間を表します。加えてあなたのスタート地点を表す頂点 \(p\) と相手のスタート地点を表す頂点 \(q\) が与えられます。
あなたと親友が一番早く会うことができる頂点 \(t\) を見つけるアルゴリズムを説明、解析してください。
-
あなたは Giggle Highway View プロジェクトのサイクリストとして雇われました。このプロジェクトでは米国の国立高速道路の写真をストリートごとに撮影します。試験的な実験として、あなたはオレゴン州ポートランドの "Giggleplex" からニューヨーク州ブルックリン区ウィリアムズバーグの "Gigglesburg" まで Giggle Highway-View 固定ギアカーボンファイバー自転車を走らせることになりました。
あなたは救いようのないカフェイン中毒なのですが、他の Giggle の従業員と同じようにコーヒーオタクでもあります: あなたが飲めるのは、日陰で育てられたオーガニックの豆を直接取引したものを、一種類だけ手で挽いて個別に焙煎して作ったエスプレッソに混じりけの無いミルクと砂糖を入れたものだけです。どうもありがとう。エスプレッソを補給すると、あなたはカフェイン離脱性片頭痛で苦しまずに自転車で \(L\) マイル進むことができます。
親切なことに、Giggle は全米中のコーヒーショップを表した無向グラフをあなたに渡してくれました。このグラフの頂点は日陰で育てられたオーガニックの豆を直接取引したものを、一種類だけ手で挽いて個別に焙煎して作ったエスプレッソを飲めるコーヒーショップを表し、辺がそれらを結ぶ高速道路を表します。各辺 \(e\) は高速道路の長さを表すラベル \(l(e)\) が付いています。二つの Giggle オフィスは頂点 \(s, t\) で表され、当然そこにはエスプレッソスタンドがあります。
-
Giggleplex から Gigglesburg までカフェイン離脱性片頭痛に苦しむことなく行けるかどうかを判定するアルゴリズムを説明、解析してください。
-
値の張るソフト帽をかぶることで、エスプレッソを補給してから自転車で進むことができる距離 \(L\) を増やせることをあなたは発見しました。Giggleplex から Gigglesburg までカフェイン離脱性片頭痛に苦しむことなく行くために必要となる最小の \(L\) の値を求めるアルゴリズムを説明、解析してください。
-
自転車で向こうのオフィスまで行くのが不可能であると (最近ライバル企業 Ünter から引き抜かれた) 上司に報告すると、彼女は地図を見せるように言いました。「あぁ、何が問題なのか分かったわ。地図にスターバックスが載ってないじゃない!」恐れおののくあなたに、彼女は全米中のスターバックスの場所を頂点として追加したグラフ \(G^{\prime}\) を渡しました。親切にも新しい頂点はスターバックスグリーン (Pantone® 3425 C) で塗られていました。
Giggleplex から Gigglesburg までカフェイン離脱性片頭痛に苦しむことなく行くときに、訪れなければならないスターバックスの数を最小値を求めるアルゴリズムを説明、解析してください。きちんと言うと、アルゴリズムの出力は \(s\) から \(t\) への長さが \(L\) 以下の辺だけを使う路の中に含まれる緑の頂点の数の最小値です。
-
-
辺に非負の重みが付いた有向グラフ \(G = (V, E)\) と二つの頂点 \(s, t\) が与えられたとします。\(G\) に含まれる \(s\) から \(t\) への辺の数が \(3\) で割り切れる歩道のうち最短のもの見つけるアルゴリズムを説明、解析してください。

例えば、辺の重みが全て \(1\) である上のグラフに対するアルゴリズムの答えは、歩道 \(s \rightarrow w \rightarrow y \rightarrow x \rightarrow s \rightarrow w \rightarrow t\) に対応する \(6\) です。
-
辺に非負の重みが付いた有向グラフ \(G = (V, E)\) が与えられ、全ての辺が赤または青に塗られているとします。\(G\) における頂点 \(s\) から頂点 \(t\) への同じ色の辺が三回以上連続しない最短の歩道の長さを計算するアルゴリズムを説明してください。つまり、歩道が二回連続して赤い辺を通ったら次の辺は青い必要があり、歩道が二回連続して青い辺を通ったら次の辺は赤い必要があるということです。
例えば入力が次のグラフで赤い辺の重みが 1、青い辺の重みが \(2\) だった場合、アルゴリズムの出力は \(s \color{red}{\,\rightarrow}\) \(a \color{red}{\,\rightarrow}\) \(b \color{#2D2F91}{\,\Rightarrow}\) \(d \color{red}{\,\rightarrow}\) \(c \color{#2D2F91}{\,\Rightarrow}\) \(a \color{red}{\,\rightarrow}\) \(b \color{red}{\,\rightarrow}\) \(t\) に対応する \(9\) です。

-
辺に非負の重みが付いた有向グラフ \(G = (V, E)\) が与えられ、\(G\) の全ての辺が赤、白、青のどれかで塗られているとします。\(G\) の歩道に含まれる辺の色が赤、白、青、赤、白、青、という順番になっているとき、その歩道をフランス国旗歩道と呼びます。きちんと言うと、歩道 \(v_{0} \rightarrow\) \(v_{1} \rightarrow\) \(\cdots \rightarrow\) \(v_{k}\) がフランス国旗歩道なのは、全ての整数 \(i\) について、辺 \(v_{i} \rightarrow v_{i+1}\) の色が \(i \mod 3 = 0\) ならば赤、\(i \mod 3 = 1\) ならば白、\(i \mod 3 = 2\) ならば青な場合です。
開始頂点 \(s\) から \(G\) の他の全ての頂点に対する最短のフランス国旗歩道を計算するアルゴリズムを説明してください。
-
\(n\) 個の銀河を結ぶ \(m\) 個の銀河間テレポートウェイがあります。各テレポートウェイは二つの銀河を結んでいて、双方向に使うことができます。また各テレポートウェイ \(e\) の運賃は \(c(e)\) ドルであり、\(c(e) > 0\) です。同じテレポートウェイを複数回使っても構いませんが、使うたびに運賃を支払う必要があります。
Judy は銀河 \(s\) から銀河 \(t\) までなるべく安く移動したいと思っています。しかし彼女は小銭を持ち歩きたくないので、運賃の合計を 5 ドルの倍数にしたいとも考えています。
-
運賃の合計が 5 ドルの倍数でなければならないという制約の下で \(s\) から \(t\) まで移動するときの最小の合計運賃を計算するアルゴリズムを説明、解析してください。
-
Judy が一回だけテレポートを無料にできるクーポンを持っているとして (a) を解いてください。
-
-
新しい街に引っ越してきたあなたは、自宅から仕事場までの徒歩の通勤ルートを決めることにしました。毎日運動ができるように、このルートは最初の部分が登り道 (運動用) で残りの部分が下り道 (休憩用) であるか、そうでなければ全てが登り道あるいは全てが下り道である必要があります (仕事場から自宅への帰り道にも同じ道を使うので、この場合でも運動ができます)。一方で仕事場に遅刻しないように、この条件を満たすルートの中で最短のものを選ぶ必要があります。
問題の入力は無向グラフ \(G\)、開始頂点 \(s\)、目標頂点 \(t\) であり、\(G\) の頂点が交差点を、辺がそれらを結ぶ道路を表します。各頂点 \(v\) には交差点の海抜を表す値 \(h(v)\) が、各辺 \(e\) には道路の長さを表す値 \(l(e)\) が付いています。
-
全ての頂点の高さが異なる場合に、\(s\) から \(t\) への最短の "登って下る" 路を求めるアルゴリズムを説明、解析してください。
-
頂点の高さが同じことがある場合に、\(s\) から \(t\) への最短の "登って下る" 路を求めるアルゴリズムを説明、解析してください。高さが変化しない辺は "登る" 部分と "下る" 部分のどちらで使っても構いません。
-
\(s\) から \(t\) への条件を満たす路が存在しないとします。\(s\) から \(t\) の路であって "登る" 道と "下る" 道の入れ替わりの回数が最小な路を考えたときに、その中で長さが最小のものを求めるアルゴリズムを説明してください。
-
-
Sham-PooBanana 大学を卒業したあなたは、飛行機が大嫌いな人のための旅行会社 Aerophobes-Я-Us に就職しました。あなたの仕事はある都市から別の都市へのフライトのプランを顧客に提示するシステムの作成です。顧客はみな飛行機での移動 (そして空港にいること) を嫌うので、プランに含まれるフライトはできるだけ短い必要があります。あなたは地球上の全てのフライトの発着時間にアクセスできるとします。
ある顧客が都市 \(X\) から都市 \(Y\) まで飛行機で移動したいとします。移動にかかる合計時間、つまり最初のフライトの出発時間から最後のフライトの到着時間までの、別のフライトを待つ時間も含めた時間が最小になるようなフライトの列を求めるアルゴリズムを説明してください。
-
練習問題 5.20 では鋭角迷路が解けるかどうかを判定するアルゴリズムを考えました。この問題では、与えられた鋭角迷路を通り抜ける最短経路を見つける問題を三つ異なる "長さ" に対して考えます。
アルゴリズムには連結無向グラフ \(G\) が与えられ、頂点が平面上の点に、辺が線分に対応します。辺は端点以外の点で交わりません。例えば X の形をした迷路には 5 個の頂点と 4 個の辺が含まれ、上図左の迷路には 18 個の頂点と 21 個の辺が含まれます。アルゴリズムには二つの頂点 \(\textsc{Start}\) と \(\textsc{Finish}\) も与えられます。
\(G\) に含まれる歩道が鋭角歩道としての条件を満たすのは、歩道の連続する任意の二つの辺 \(u \rightarrow v \rightarrow w\) について \(\angle uvw = \pi\) または \(\angle uvw < \pi / 2\) なときです。辺を二つ受け取ってそれらが直線か、鈍角か、鋭角かを \(O(1)\) 時間で判定するサブルーチンを使えると仮定してください。
-
\(\textsc{Start}\) と \(\textsc{Finish}\) への条件を満たす路の中で線分の数が最小になるものを計算するアルゴリズムを説明してください。
-
\(\textsc{Start}\) と \(\textsc{Finish}\) への条件を満たす路の中で方向転換の数が最小になるものを計算するアルゴリズムを説明してください。 [ヒント: この問題は (a) と同じではありません]
-
\(\textsc{Start}\) と \(\textsc{Finish}\) への条件を満たす路の中で辺のユークリッド距離が最小になるものを計算するアルゴリズムを説明してください。 任意の線分の長さを \(O(1)\) 時間で計算できるとしてください。
-
-
See-Bull Center for Fake News Detection で行われた難しい中間試験を終えて、あなたはバスで家に帰ろうとしています。バスで帰ることになると分かっていたので、あなたは Sham-PooBanana の街の中を走る全てのバスがいつどの停留所に停まるかをまとめた表を持っています。残念ながら See-Bull Center から自宅まで直接行くバスはないので、最低でも一度はバスを乗り換える必要があります。全部で \(b\) 台のバスが走っており、全てのバスは 12:00:01 AM に出発し、\(n\) 個の停留所を回り、11:59:59 PM に最後の停留所に停まります。バスはスケジュールに従って正確に運行され、あなたは正確な時計を持っています。またあなたは疲れ切っているので停留所の間を歩くことはできません。
-
家になるべく早く着くようなバスの列を計算するアルゴリズムを説明、解析してください。最小化するのは到着時間であって、See-Bull Center から家まで行くのにかかる時間ではありません。
-
大変です!中間試験はハロウィーンに行われたので、道がゾンビであふれています!残念ながら、Sham-PooBanana の公共交通機関担当の部署には一年のうちたった一夜のためにバスを追加したりゾンビお断りのバス停留所を設置したりするための予算がありません。バスの停留所で過ごす時間を最小化するようなバスの列を計算するアルゴリズムを説明、解析してください。家に着くのが遅くなったり、バスに乗っている時間が長くなったりしても構いません。また最初にバスに乗るまでは See-Bull Center で安全に待つことができるので、最初のバスに乗るまでの時間はカウントしません。
-
-
夢のような春休みから帰った次の朝、Alice が目覚めると車が動かなくなっていました。彼女は Sham-PooBanana 大学の講義に公共交通機関を使って出席しなければなりません。PooBanana 地方のバスの完全な運行表を彼女は持っています。運行表の中でバスの運行ルートは有向グラフ \(G\) で表され、頂点が停留所を、辺がそれらの間の運行ルートを表します。各辺 \(u \rightarrow v\) について、運行表には次に示す三つの正の実数が書かれています:
-
\(l(u \rightarrow v)\) は停留所 \(u\) から停留所 \(v\) へのバスを使った移動にかかる時間 (分) を表す。
-
\(f(u \rightarrow v)\) は停留所 \(u\) から停留所 \(v\) に向かって出発するバスの最初の出発時間 (12:00 AM からの相対時刻) を表す。
-
\(\Delta(u \rightarrow v)\) は停留所 \(u\) から停留所 \(v\) に向かって出発する二つの連続するバス同士の出発時間の間隔 (分) を表す。
つまり、\(u\) を \(v\) に向かって最初に出発するバスは時刻 \(f(u \rightarrow v)\) に \(u\) を出発し、時刻 \(f(u \rightarrow v) + l(u \rightarrow v)\) に \(v\) に到着します。同じ区間の二本目のバスは時刻 \(f(u \rightarrow v) + \Delta(u \rightarrow v)\) に \(u\) を出発し、\(f(u \rightarrow v) + \Delta(u \rightarrow v) + l(u \rightarrow v)\) に \(v\) に到着します。三本目のバスは時刻 \(f(u \rightarrow v) + 2 \cdot \Delta(u \rightarrow v)\) に \(u\) を出発し、\(f(u \rightarrow v) + 2 \cdot \Delta(u \rightarrow v) + l(u \rightarrow v)\) に \(v\) に到着します。
Alice が目的地に着くことができる一番早い時刻を求めるアルゴリズムを説明、解析してください。アルゴリズムの入力はグラフ \(G = (V, E)\) と頂点 \(s, t\) 、各辺 \(e \in E\) に対する \(l(e), f(e), \Delta(e)\) の値、そして Alice が家を出る時間 (12:00 AM からの相対時刻) です。
[ヒント: このレアなインスタンスでは、入力グラフを改変するよりもアルゴリズムを改変した方が簡単かもしれません。]
-
-
Mulder と Scully はアメリカ中の全ての道路について、その道路を車で走っている人がエイリアンに誘拐される確率を正確に計算しました。そして Mulder 捜査官は バージニア州 Langley からネバダ州の Area 51 まで車で移動することになりました。どうすればエイリアンに誘拐される確率を最小化できるでしょうか?
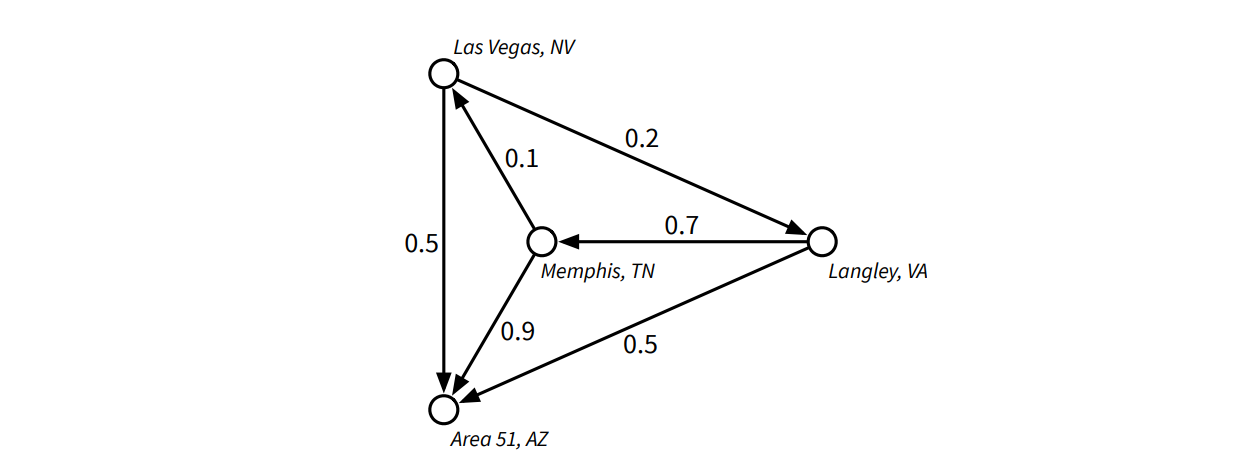
きちんと問題を定義すると、グラフ \(G = (V, E)\) が与えられ、各辺 \(e\) が安全さを表す互いに独立な確率 \(p(e)\) を持っているとします。\(G\) の路の安全性をその辺の安全性の積と定義したときに、与えられた頂点 \(s\) から \(t\) への路の中で最も安全性の高いものを計算するアルゴリズムを説明、解析してください。必要になる算術演算は全て \(O(1)\) 時間で実行できるとしてください。
例えば道路と確率が上図のようになっている場合、Mulder が Langley から Area 51 に直接行った場合は 50 % の確率で誘拐されずにたどり着くことができます。また Memphis を経由していけば、0.7 × 0.9 = 63 % の確率で安全にたどり着けます。しかしもし Memphis と Las Vegas を経由するようにした場合、彼は 1 - 0.7 × 0.1 × 0.5 = 96.5 % の確率で (Elvis のように) 誘拐されてしまいます!
-
♣ Sunnydale 国立公園で行われた宿泊キャンプ旅行で、あなたは叫び声を聞いて落ち着かない眠りから目を覚ましました。何が起きたのかとテントの周りを探っていると、森の中から怯え切った血まみれの公園の警備員がくしゃくしゃの紙を胸に抱えて走ってきました。彼はあなたのテントに近づくと、「逃げろ......るうちに...」という言葉と共に紙をあなたに渡し、そのまま倒れてしまいました。脈を調べたところ、その警備員は完全に息を引き取っていました。
渡された紙を確認すると、その紙が公園の地図であることが分かりました。地図は無向グラフであり、頂点が公園の目印となるものを、辺がそれらの間の歩道を示しています (歩道は頂点同士をつなぐだけで、重なったりしません)。あなたは自分が今いる頂点を見つけることができました。地図の端にある頂点のいくつかには EXIT の印が付いています。
紙をさらによく調べると、誰か (おそらくは今死亡した哀れな公園警備員) によって頂点と辺に \(0\) から \(1\) の実数が書かれていることに気が付きました。地図の裏に走り書きされたメモによると、辺に書かれた数値は対応する歩道を歩いているときに怪物に襲われる確率であり、頂点に書かれた数値は対応する目印にいるときに怪物に襲われる確率であるようです (怪物は必ず単独で行動するので、同時刻に同じ歩道および目印に二匹以上の怪物がいることはありません)。紙には辺で示した歩道から出るとゆっくりとした悲惨な死が待っているという警告もあります。
あなたは足元の死体に目をやりました。確かに彼の死は悲惨というほかありません。待てよ、今動いたか? 歯が伸びていっていないか? あなたはテントの杭を死体の心臓に突き刺して、頭をフル回転させて最短経路で公園から逃げることを決めました。
現在位置から適当な出口までの路の中で怪物との遭遇回数の期待値が最小になるものを求める効率の良いアルゴリズムを説明、解析してください。 [ヒント: 頂点に確率が無かったとしても、この問題は前問と同じではありません!]
