スベテの辺を緩和する: Bellman-Ford
Ford の一般的な最短路アルゴリズムの一番単純な実装のアイデアは、1954 年に Alfonso Shimbel (アルフォンソ・シンベル) によって提案され、1957 年に Edward Moore (エドワード・ムーア) によってより詳細に示されました。同じアルゴリズムは 1957 年には Max Woodbury (マックス・ウッドベリー) と George Dantzig (ジョージ・ダンツィグ) によって、1958 年には Richard Bellman (リチャード・ベルマン) によって、同じく 1958 年に Geroge Minty (ジョージ・ミンティ) によってそれぞれ独立に発見されています (Woodbury も Dantzig も Minty もアルゴリズムを発表することはありませんでした)。スティグラーの法則に完璧に従って、このアルゴリズムは Bellman-Ford のアルゴリズム1 として世界中に知られています。こう呼ばれているのは、1956 年に Ford によって発表された辺の緩和を使った定式化について Bellman がはっきりと言及していたためです。ただし "Bellman-Kalaba" という名前2を使う著者もいますし、古い文献には "Bellman-Shimbel" という名前も出てきます。
Shimbel / Moore / Woodbury-Dantzig / Bellman-Ford / Kalaba / Minty / Brosh3 のアルゴリズムは次の一行に要約できます:
Bellman-Ford: 緊張している辺をスベテ緩和し、再帰する。
procedure \(\texttt{BellmanFord}\)(\(s\))
\(\texttt{InitSSSP}\)(\(s\))
while 緊張している辺が一つでもある do
for \(u \rightarrow v\) の形をした辺 do
if \(u \rightarrow v\) が緊張している then
\(\texttt{Relax}\)(\(u \rightarrow v\))
任意の頂点 \(v\) と非負整数 \(i\) に対して、 \(G\) における辺を \(i\) 個以下しか使わない \(s\) から \(v\) への最短の歩道の長さを \(\pmb{\mathit{dist}_{\leq i}(v)}\) と表すことにします。例えば \(\mathit{dist}_{\leq 0}(s) = 0\) および全ての \(v \neq s\) について \(\mathit{dist}_{\leq 0}(v) = \infty \) です。Bellman-Ford の正しさと効率の証明において鍵となるのは次の命題です。
命題 8.6 \(v\) を任意の頂点、\(i\) を非負整数とする。\(\textsc{BellmanFord}\) のメインループの \(i\) 回目の反復が終了した時点において、\(\mathit{dist}(v) \leq \mathit{dist}_{\leq i} (v)\) が成り立つ。
証明 \(i\) についての帰納法で示す。\(i = 0\) の場合は自明だから、\(i > 0\) とする。\(v\) を適当な頂点とし、頂点を \(i\) 個以下しか含まない \(s\) から \(v\) への最短歩道を \(W\) とする (最短の歩道がいくつかある場合は適当に選ぶ)。定義により \(W\) の長さは \(\mathit{dist}_{\leq i} (v)\) に等しい。考えるべきケースは二つある。
-
\(W\) に辺が含まれないとき、\(W\) は \(s\) から \(s\) への自明な歩道だから、\(v = s\) かつ \(\mathit{dist}_{\leq i}(s) = 0\) である。\(\textsc{InitSSSP}\) において \(\mathit{dist}(s) \leftarrow 0\) と代入し、\(\mathit{dist}(s)\) はそれ以降増加しないので \(\mathit{dist}(s) \leq 0 = \mathit{dist}_{\leq i}(s)\) が成り立つ。
-
そうでないとき、\(W\) の最後の辺を \(u \rightarrow v\) とする。帰納法の仮定により、\(i - 1\) 回の反復の後 \(\mathit{dist}(u) \leq \mathit{dist}_{\leq i-1}(u)\) が成り立っている。\(i\) 回目の反復では \(\mathit{dist}(v) \leq \mathit{dist}(u) + w(u \rightarrow v)\) が最初から成り立っているか、そうでなければ \(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + w(u \rightarrow v)\) という代入が行われる。いずれの場合でも、\(\mathit{dist}(v) \leq \mathit{dist}(u) + w(u \rightarrow v)\) が成り立つ。加えて \(\mathit{dist}(v)\) はこの反復で増加しないので、\(\mathit{dist}(v) \leq\) \(\mathit{dist}(u) + w(u \rightarrow v) =\) \(\mathit{dist}_{\leq i} (v)\) が成り立つ。
いずれの場合でも、\(i\) 回目の反復が終わったとき \(\mathit{dist}(v) \leq \mathit{dist}_{\leq i}(v)\) が成り立つ。 \(\Box\)
入力グラフに負閉路が存在しないなら、\(s\) から任意の頂点への最短路は最大でも \(V-1\) 個の辺を持つ単純路です。よって \(\textsc{BellmanFord}\) は最大でも \(V-1\) 回の反復で正しい最小路を計算して停止します。言い方を変えれば、もし \(V-1\) 回の反復を行ってもなお緊張している辺が残っているなら、入力グラフは負閉路を持ちます! このことを使えば、アルゴリズムを次のように書き換えて、負閉路を見つけたときにエラーを出すようにできます。
このアルゴリズムの内側の反復は明らかに \(O(E)\) だけ時間がかかるので、全体の実行時間は \(\pmb{O(VE)}\) です。またこの Bellman-Ford のアルゴリズムの実装は負辺がある場合でも、さらには負閉路がある場合でも効率良く計算を行えます。
procedure \(\texttt{BellmanFord}\)(\(s\))
\(\texttt{InitSSSP}\)(\(s\))
for \(V - 1\) 回繰り返す do
for \(u \rightarrow v\) の形をした辺 do
if \(u \rightarrow v\) が緊張している then
\(\texttt{Relax}\)(\(u \rightarrow v\))
for 辺 \(u \rightarrow v\) do
if \(u \rightarrow v\) が緊張している then
return "入力グラフに負閉路がある!"
しかし辺の重みが非負である場合には、少なくとも最悪計算時間は Dijkstra のアルゴリズムの方が速くなります (ただ実際にプログラムを動かすと、負辺が含まれるグラフであっても Dijkstra のアルゴリズムの方が Bellman-Ford のアルゴリズムよりも速くなることが多いです)。
Moore による改善
Moore も Bellman も、ここに説明した Bellman-Ford アルゴリズムを示したわけではありませんでした。Moore は重み無しグラフに対する幅優先探索 ("Algorithm A") を発表したのと同じ論文で、彼のバージョンの Bellman-Ford アルゴリズム ("Algorithm D") を示しています。Moore のアルゴリズムの最悪計算量は \(O(VE)\) で \(\textsc{BellmanFord}\) と変わりませんが、Moore のアルゴリズムは "明らかに" 緊張していない辺を飛ばすので、現実のデータに対しては \(\textsc{BellmanFord}\) よりも各段に速いことが多いです。このアルゴリズムを次に示します:
procedure \(\texttt{Moore}\)(\(s\))
\(\texttt{InitSSSP}\)(\(s\))
\(\texttt{Push}\)(\(s\))
⟨⟨最初のフェーズを始める⟩⟩
\(\texttt{Push}\)(\(\color{red}{\bigstar}\))
while キューに少なくとも一つの頂点がある do
\(u \leftarrow \)\(\texttt{Pull}\)()
if \(\color{red}{u = \bigstar}\) then
⟨⟨フェーズが終わったので、次のフェーズを始める⟩⟩
\(\texttt{Push}\)(\(\color{red}{\bigstar}\))
else
for \(u \rightarrow v\) の形をした辺 do
if \(u \rightarrow v\) が緊張している then
\(\texttt{Relax}\)(\(u \rightarrow v\))
if \(v\) がキューに無い then
\(\texttt{Push}\)(\(v\))
Moore は幅優先探索に二つの変更を加えることで最短路アルゴリズムを作っています。まず辺の重みを考えるために内側のループの \(+ \ 1\) を \(+ \ w(u \rightarrow v)\) で置き換え、次にキューに同じ頂点が複数入ることが無いように \(\textsc{Insert}\) の前にキューの中を調べます4。
前に幅優先探索 (BFS) に対して行ったのと同じように、解析を簡単にするためのトークンを導入してアルゴリズムの実行を複数のフェーズに分けます。BFS と同じように、トークンがキューに \(\textsc{Push}\) されるときにフェーズが始まり、トークンがキューから \(\textsc{Pull}\) されたときにフェーズが終わります。そしてキューがトークンだけになったらアルゴリズムの終わりです。
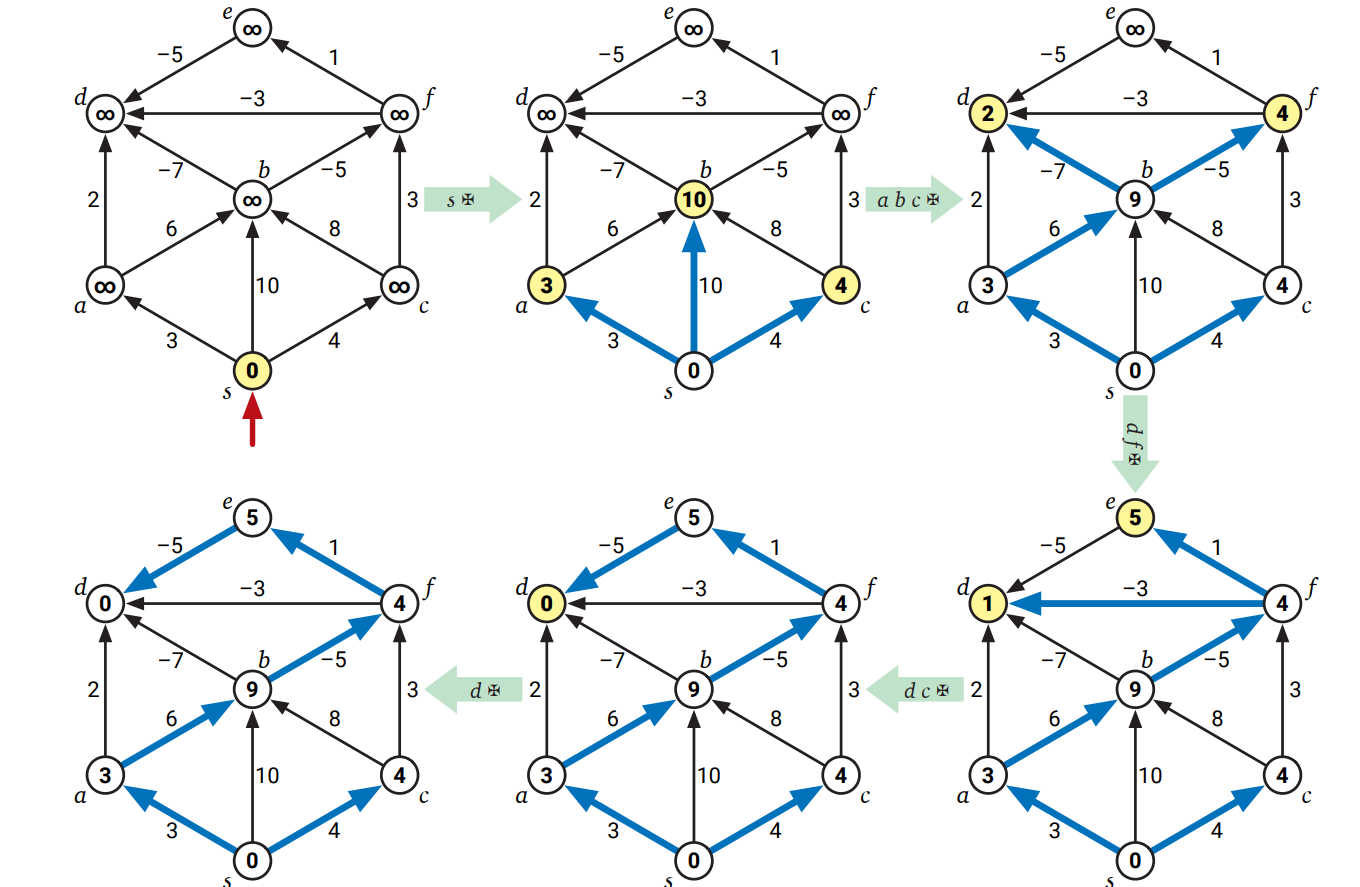
任意の時点でキューには同じ頂点のコピーが多くとも一つしか含まれず、キューにある全ての頂点はフェーズごとに最大一度だけ \(\textsc{Pull}\) されるので、各フェーズで辺 \(u \rightarrow v\) は多くとも一回しか緊張しているかどうかのチェックを受けません。さらにフェーズが始まった時点で緊張している辺は全てそのフェーズで緩和されます (フェーズ中に緊張した辺が同じフェーズ中に緩和されることはあり得ます。またフェーズ中に緩和された辺がそのフェーズ中に緊張することもあり得ます)。
\(\textsc{BellmanFord}\) は全ての辺を総当たりで調べていたので、以上の説明により、\(\textsc{Moore}\) はキューを使って辺を管理するように改善した \(\textsc{BellmanFord}\) と言うことができます。以前と同様の帰納法による証明を使うと、命題 8.6 と同様の命題を示せます:
命題 8.7 任意の頂点 \(v\) と非負整数 \(i\) について、\(\textsc{Moore}\) の \(i\) 番目のフェーズが終わったとき \(\mathit{dist}(v) \leq \mathit{dist}_{\leq i} (v)\) が成り立つ。
よってグラフに負閉路が無いならば、\(\textsc{Moore}\) は最大 \(V-1\) 回のフェーズの後に停止します。各フェーズにおいて各頂点は最大でも一回スキャンされ、各辺は最大でも一回緩和されるので、一度のフェーズの最悪計算時間は \(O(E)\) であり、\(\textsc{Moore}\) アルゴリズム全体の実行時間は \(\pmb{O(VE)}\) です。しかし実際に実装すると、\(\textsc{Moore}\) は \(\textsc{BellmanFord}\) よりもはるかに速く最短路を計算します。\(\textsc{Moore}\) はそれまでのフェーズで \(\mathit{dist}(u)\) が変化した辺 \(u \rightarrow v\) だけをスキャンするからです。
入力グラフに負閉路がある場合、\(\textsc{Moore}\) は停止しません。ですが幸運にも、\(\textsc{BellmanFord}\) と同じように \(\textsc{Moore}\) を負閉路がある場合にはそれを報告するように簡単に変更できます。おそらく一番簡単な方法は、実際にトークンを管理して、トークンをキューから \(\textsc{Pull}\) した回数を数えるというものでしょう。こうすると、入力グラフに負閉路があることは、\(n-1\) 個目のトークンをキューから \(\textsc{Pull}\) した直後にキューが空でないことと同値になります。
動的計画法による定式化
彼の名前の付いたほとんど全てのものと同じように、Richard Bellman は "Bellman-Ford" の最短路アルゴリズムの導出に動的計画法を使いました。以前と同様に最短路の長さの再帰的な定義を最初に考えましょう。もしかすると、有向非巡回グラフに対して使ったのと同じ、次の等式を使いたくなるかもしれません: \[ \mathit{dist}(v) = \begin{cases} 0 & \text{if } v = s \\ \min\limits_{u \rightarrow v} (\mathit{dist}(u) + w(u \rightarrow v)) & \text{それ以外} \end{cases} \] 残念ながら、グラフが DAG でない場合、この再帰方程式は正しくありません! グラフに閉路 \(u \rightarrow v \rightarrow w \rightarrow u\) が含まれるとすると、\(\mathit{dist}(w)\) を計算するにはまず \(\mathit{dist}(v)\) を計算しなくてはならず、\(\mathit{dist}(v)\) のためには \(\mathit{dist}(u)\) の値が必要ですが、\(\mathit{dist}(u)\) のためには \(\mathit{dist}(w)\) が必要となります。つまり、グラフに閉路が含まれると無限ループになってしまいます!
正しい再帰方程式を得るには、グラフの構造に関するパラメータを関数に渡す必要があります。このパラメータは再帰的な呼び出しのたびにひとつずつ減っていき、0 になったときの関数の値は自明となるようなパラメータです。Bellman は路が含むことができる辺の最大数を追加のパラメータとして選びました5。
前述の解析と同じように、\(\mathit{dist}_{\leq i}(v)\) で \(s\) から \(v\) への辺が \(i\) 個以下の歩道の中で最短のものの長さを表すことにします。Bellman が気付いたのは、この関数が満たす次の Bellman の等式 再帰方程式です: \[ \mathit{dist}_{\leq i}(v) = \begin{cases} 0 & \text{if } i = 0 \text{ and } v = s \\ \infty & \text{if } i = 0 \text{ and } v \neq s \\ \min \left\lbrace \begin{array}{c} \mathit{dist}_{\leq i - 1}(v) \\ \min\limits_{u \rightarrow v} (\mathit{dist}_{\leq i - 1} (u) + w(u \rightarrow v)) \end{array} \right\rbrace & \text{ それ以外} \end{cases} \]
グラフに負閉路が無いとすると、最短路問題の目標は全ての頂点 \(v\) に対する \(\mathit{dist}_{\leq V - 1}(v)\) の計算です。この再帰方程式を動的計画法を使って計算するアルゴリズムを次に示します。ここで \(\mathit{dist}[i, v]\) が \(\mathit{dist}_{\leq i} (v)\) の値を保持します。最終的に計算される最短路の長さの正しさは再帰方程式の正しさから従います。また実行時間が \(O(VE)\) であるのは明らかです。
procedure \(\texttt{BellmanFordDP}\)(\(s\))
\(\mathit{dist}[0, s] \leftarrow 0\)
for 頂点 \(v \neq s\) do
\(\mathit{dist}[0,v] \leftarrow \infty\)
for \(i \leftarrow 1\) to \(V - 1\) do
for 頂点 \(v\) do
\(\mathit{dist}[i, v] \leftarrow \mathit{dist}[i - 1, v]\)
for \(u \rightarrow v\) の形をした辺 do
if \(\mathit{dist}[i, v] > \mathit{dist}[i-1, u] + w(u \rightarrow v)\) then
\(\mathit{dist}[i,v] \leftarrow \mathit{dist}[i-1, u] + w(u \rightarrow v)\)
以上が Bellman が示した最短路のアルゴリズムの本質的な部分です。この動的計画法のアルゴリズムを少しずつ変更していって先に示した \(\textsc{BellmanFord}\) に書き換える方法をこれから示します。まず、一番内側のループは各辺 \(u \rightarrow v\) を一回ずつ考えていますが、その順番は重要でないので、最後の三行のインデントを一つ無くすことができます。こうすることで辺を調べる順番が変わるかもしれませんが、それでも全ての \(i\) と \(v\) に対して \(\mathit{dist}_{\leq i} (v)\) が正しく計算されます。
procedure \(\texttt{BellmanFordDP2}\)(\(s\))
\(\mathit{dist}[0, s] \leftarrow 0\)
for 頂点 \(v \neq s\) do
\(\mathit{dist}[0,v] \leftarrow \infty\)
for \(i \leftarrow 1\) to \(V - 1\) do
for 頂点 \(v\) do
\(\mathit{dist}[i, v] \leftarrow \mathit{dist}[i - 1, v]\)
for \(u \rightarrow v\) の形をした辺 do
if \(\color{red}{\mathit{dist}[i, v] > \mathit{dist}[i-1, u] + w(u \rightarrow v)}\) then
\(\color{red}{\mathit{dist}[i,v] \leftarrow \mathit{dist}[i-1, u] + w(u \rightarrow v)}\)
次に最後の二行の添え字を \(i-1\) から \(i\) に変えます。これによって全ての \(i, v\)に対して \(\mathit{dist}[i,v] {\color{red}{ = }} \mathit{dist}_{\leq i} (v)\) ではなく \(\mathit{dist}[i,v] {\color{red}{\leq}} \mathit{dist}_{\leq i} (v)\) が成り立つようになるので、\(\mathit{dist}[i,v]\) が最短路の真の長さにより速く近づくようになります。この関係が成り立つのは 命題 8.6 と 命題 8.7 から分かります。
procedure \(\texttt{BellmanFordDP3}\)(\(s\))
\(\mathit{dist}[0, s] \leftarrow 0\)
for 頂点 \(v \neq s\) do
\(\mathit{dist}[0,v] \leftarrow \infty\)
for \(i \leftarrow 1\) to \(V - 1\) do
for 頂点 \(v\) do
\(\mathit{dist}[i, v] \leftarrow \mathit{dist}[i - 1, v]\)
for \(u \rightarrow v\) の形をした辺 do
⟨⟨\(i-1\) でない!⟩⟩
if \(\mathit{dist}[i, v] > \mathit{dist}[{\color{red}{i}}, u] + w(u \rightarrow v)\) then
\(\mathit{dist}[i,v] \leftarrow \mathit{dist}[{\color{red}{i}}, u] + w(u \rightarrow v)\)
しかし考えてみると、このアルゴリズムはすこし馬鹿なことをしています。というのも、外側のループの反復が \(\mathit{dist}[\ast, \ast]\) の \(i-1\) 行目を \(i\) 行目にコピーすることから始まり、その後 \(i\) 行目の要素しか使わないのです。つまり二次元配列は不必要で、反復のための添え字 \(i\) は余分です! 最後の変更として、暫定的な距離を一次元配列だけを使って管理するようにします:
procedure \(\texttt{BellmanFordFinal}\)(\(s\))
\(\mathit{dist}{\color{red}{[s]}} \leftarrow 0\)
for 頂点 \(v \neq s\) do
\(\mathit{dist}{\color{red}{[v]}} \leftarrow \infty\)
for \(i \leftarrow 1\) to \(V - 1\) do
for \(u \rightarrow v\) の形をした辺 do
if \(\mathit{dist}{\color{red}{[v]}} > \mathit{dist}{\color{red}{[u]}} + w(u \rightarrow v)\) then
\(\mathit{dist}{\color{red}{[v]}} \leftarrow \mathit{dist}{\color{red}{[u]}} + w(u \rightarrow v)\)
最終的な動的計画法のアルゴリズムは \(\textsc{BellmanFord}\) の最初の定式化とほとんど同一です! 最初の三行が最短路距離を初期化し、最後の二行が緊張した辺を緩和しています。\(\textsc{BellmanFordFinal}\) には前者へのポインタの管理と閉路の検出という機能がありませんが、幸いにもこの機能を追加するのは簡単です。
-
歴史的に不正確なのは承知で、私はこの慣習に従います。 "Shimbel / Moore / Woodbury-Dantzig / BellmanFord / Kalaba / Minty のアルゴリズム" と書いてあるのを読みたい人はいないでしょうし、"Shimbel's algorithm" について話していると相手が不思議な目でこちらを見てくるのはもうごめんです。[return]
-
この名前が指しているのは Richard Bellman と Robert Kalaba (ロバート・カラバ) によって 1956 年に書かれた動的計画法と制御理論に関する専門書のことで、Bellman のアルゴリズムがこの本で説明されています。Bellman と Kalaba は任意の \(k\) に対して \(k\) 番目に短い路を計算する Bellman のアルゴリズムを拡張したアルゴリズムを 1960 年に発表しています。[return]
-
Hyperbole and a Half をもう一度全部読んでください。それから新しく猫を引き取って、もう一冊本を買えるようにしてください。[return]
-
このチェックをしなくても Moore のアルゴリズムは正しく動きますが、このチェックをしないと \(O(VE)\) の実行時間が保証されなくなります。[return]
-
次の章で見ますが、このパラメータが唯一の選択肢というわけではありません。[return]