重み無しグラフ: 幅優先探索

最も単純な最短路問題は全ての辺の重みが \(1\) で、路の長さが辺の数に等しい場合です。この特殊ケースではこれまでに説明したグラフ探索アルゴリズムの一つ幅優先探索 (breadth-first search, BFS) を使って答えを見つけられます。

幅優先探索は Edward Moore (エドワード・ムーア) によって発見されたとされることが多いです。実際彼は幅優先探索を ("Algorithm A" として) 1957 年に発表しており、これは初めて公表された迷路の最短路を見つけるための手続きです¹。VLSI の配線やロボットの経路計画の文脈では、幅優先探索が Chin Yang Lee (チン・ヤン・リー) によって発見されたとされることもあります。彼が 1961 年に Moore の "Algorithm A" の応用を (きちんと Moore に言及して) いくつか発表しているためです。しかし Konrad Zuse (コンラート・ツーゼ) は 1945 年、Moore が迷路について考えを巡らせる十年以上前に、非連結グラフの成分を数えてラベルを付ける処理の幅優先探索の実装を提案しています³。

幅優先探索では頂点を要素とする先入れ先出しのキューを管理します。最初このキューにはソース頂点 \(s\) だけが含まれ、各反復においてアルゴリズムはキュー先端から頂点 \(u\) を \(\textsc{Pull}\) し、\(u\) から伸びる辺 \(u \rightarrow v\) を調べます。この外に向かう辺 \(u \rightarrow v\) が緊張している場合にはその辺を緩和させてから頂点 \(v\) をキューに \(\textsc{Push}\) し、キューが空になった時点でアルゴリズムは終了します:

procedure \(\texttt{BFS}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

\(\texttt{Push}\)(\(s\))

while キューが空でない do

\(u \leftarrow \)\(\texttt{Pull}\)()

for \(u \rightarrow v\) の形をした辺 do

if \(\mathit{dist}(v) > \mathit{dist}(u) + 1\) then

⟨⟨緊張している辺 \(u \rightarrow v\) を緩和する⟩⟩

\(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + 1\)

\(\mathit{pred}(v) \leftarrow u\)

\(\texttt{Push}\)(\(v\))

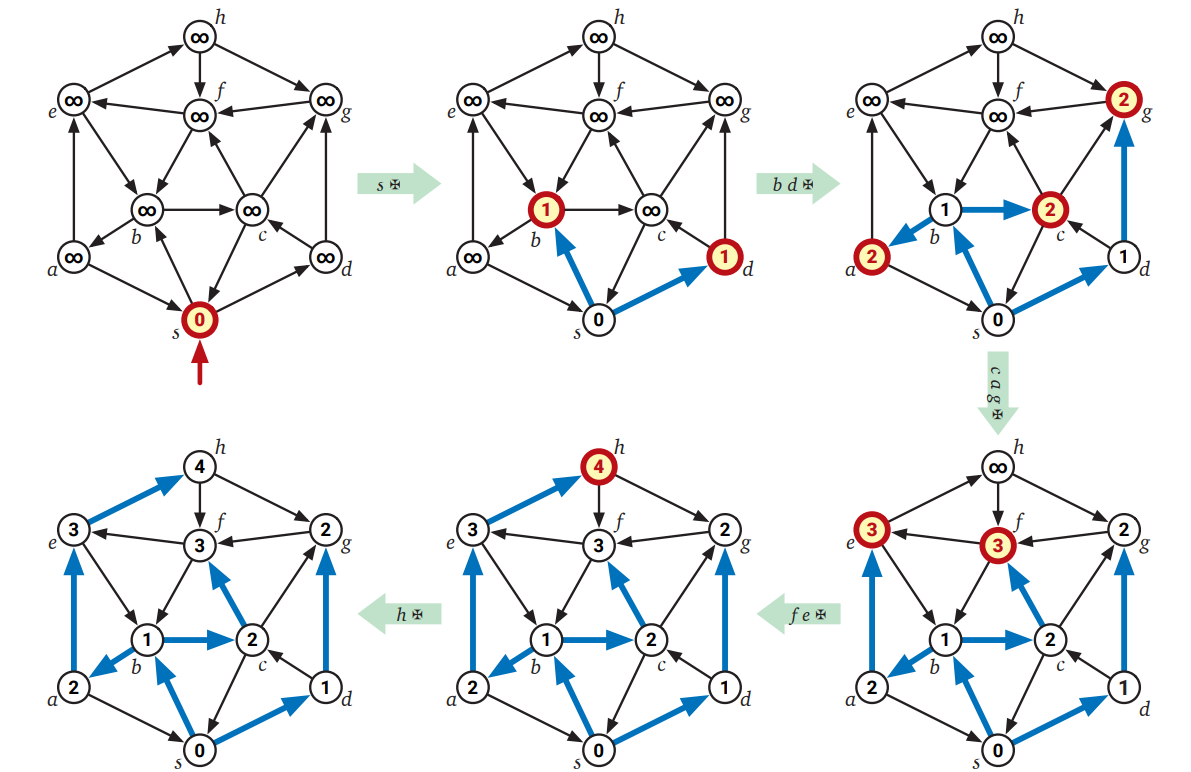
幅優先探索の解析を簡単にするために、想像上の "トークン" を考えて実行をいくつかのフェーズに分けることにします。最初に頂点を \(\textsc{Pull}\) する前にトークンをキューに \(\textsc{Push}\) しておき、その後トークンを \(\textsc{Pull}\) したときを最初のフェーズの終了とします。フェーズが終了したらすぐにトークンを \(\textsc{Push}\) して次のフェーズを始めます。こうすると最初のフェーズではソース頂点 \(s\) がスキャンされ、次のフェーズでは \(s\) に隣接する頂点がスキャンされます。アルゴリズムが終了するのはキューがトークンだけになったときです。このアルゴリズムとその実行例を以下に示します。次の点を強調しておきます: このトークンは解析を簡単にするためだけに追加されたものであり、このアルゴリズムはトークンの有無に関わらず、同じ頂点を同じ順番で \(\textsc{Push}\) および \(\textsc{Pull}\) し、出力される長さ \(\mathit{dist}\) と前者 \(\mathit{pred}\) は変化しません。

procedure \(\texttt{BFSWithToken}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

\(\texttt{Push}\)(\(s\))

⟨⟨最初のフェーズを始める⟩⟩

\(\texttt{Push}\)(\(\color{red}{\bigstar}\))

while キューに少なくとも一つの頂点がある do

\(u \leftarrow \)\(\texttt{Pull}\)()

if \(\color{red}{u = \bigstar}\) then

⟨⟨フェーズが終わったので、次のフェーズを始める⟩⟩

\(\texttt{Push}\)(\(\color{red}{\bigstar}\))

else

for \(u \rightarrow v\) の形をした辺 do

if \(\mathit{dist}(v) > \mathit{dist}(u) + 1\) then

⟨⟨緊張している辺 \(u \rightarrow v\) を緩和する⟩⟩

\(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + 1\)

\(\mathit{pred}(v) \leftarrow u\)

\(\texttt{Push}\)(\(v\))

図 8.5

フェーズの終わりを表すトークン \(\bigstar\) を追加した幅優先探索 (赤い部分は解析のためだけにある)

次の命題を示すにあたって、次のことを強調しておきます: \(\mathit{dist}(v)\) はアルゴリズムによって管理されるただの変数です。この値が暫定的な最短路の長さを表すのは直感的には明らかですが、この時点では (まだ) \(\mathit{dist}(v)\) が \(s\) から \(v\) への最短路の長さと等しいかは分かりません。すぐに示すので心配しないでください。

命題 8.1 \(i \geq 0\) を任意の整数として、 \(i\) 番目のフェーズが終わった瞬間を考える。\(v\) を任意の頂点とすると、\(\mathit{dist}(v) = \infty\) であるか、そうでなければ \(\mathit{dist}(v) \leq i\) である。そして \(v\) がキューにあるときに限って \(\mathit{dist}(v) = i\) である。

証明 \(i\) についての帰納法で示す。\(i = 0\) の場合はすぐに分かる: 最初のフェーズが始まる直前 ("0 番目のフェーズが終わったとき") キューにはソース頂点 \(s\) とトークン \(\bigstar\) だけが含まれ、\(\textsc{InitSSSP}\) によって \(\mathit{dist}(s) \leftarrow 0\) が代入され、さらに \(v \neq s\) に対しては \(\mathit{dist}(v) \leftarrow \infty\) が代入される。よって命題が成り立つ。

\(i > 0\) を適当に選ぶ。 \(i\) 番目のフェーズが始まる直前を考えると、帰納法の仮定からキューに含まれる全ての頂点 \(u\) について \(\mathit{dist}(u) = i - 1\) であり、最後に \(\bigstar\) がある。つまりキューは次のような形をしている: \[ \rightarrow \ \ \bigstar \ \ i - 1 \ \ \cdots \ \ i - 1 \ \ \rightarrow \] したがってキューから \(\bigstar\) を \(\textsc{Pull}\) して \(i\) 番目のフェーズが終了するとき、アルゴリズムは \(\mathit{dist}(u) = i - 1\) である頂点 \(u\) を全て \(\textsc{Pull}\) している。

このフェーズで \(\textsc{Pull}\) される任意の頂点 \(u\) に対して、\(u\) から離れる辺 \(u \rightarrow v\) を考える。\(u \rightarrow v\) が緊張しているならば \(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + 1\) が実行されるので \(\mathit{dist}(v) = i\) となり、その後 \(v\) はキューに \(\textsc{Push}\) される。\(i\) 番目のフェーズで距離のラベル \(\mathit{dist}(v)\) を書き換える処理はこの部分だけだから、キューには距離のラベルが \(i-1\) の頂点、トークン、\(i\) の頂点という順番で要素が並ぶ: \[ \rightarrow \ \ i \ \ \cdots \ \ i \ \ \bigstar \ \ i - 1 \ \ \cdots \ \ i - 1 \ \ \rightarrow \] よって \(i\) 番目のフェーズが終わったときにはキューにはトークンの後ろに距離のラベルが \(i\) の頂点だけが並ぶことになる: \[ \rightarrow \ \ i \ \ \cdots \ \ i \ \ \bigstar \ \ \rightarrow \]

さらに、頂点 \(v\) が最終的なキューに現れることは \(i\) 番目のフェーズで \(v\) の距離のラベルが書き換わったことと同値である。したがって \(i\) 番目のフェーズの終わったときキューには \(\mathit{dist}(v) = i\) の点が全て含まれる。また \(\mathit{dist}(v) \leq i\) も以上の議論より明らか。 \(\Box\)

命題 8.1から、\(\textsc{BFS}\) のメイン処理が距離のラベルを非減少に割り当てていくことが分かります。一方で各頂点 \(v\) に対して \(\mathit{dist}(v)\) は増加しません。また各頂点 \(v\) に対して \(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + 1\) という命令は \(\mathit{dist}(v)\) 番目のフェーズで最大でも一回しか実行されないことも示せます。同様に次のことも分かります:

\(\mathit{dist}(v)\) 番目のフェーズ中、前者へのポインタ \(\mathit{pred}(v)\) は最大でも一回しか変更されない。
\(\mathit{dist}(v)\) 番目のフェーズ中、\(v\) は最大でも一回しか \(\textsc{Push}\) されない。
\(\mathit{dist}(u) + 1\) 番目のフェーズ中、\(u\) は最大でも一回しか \(\textsc{Pull}\) されない。
\(\mathit{dist}(u) + 1\) 番目のフェーズ中、任意の辺 \(u \rightarrow v\) に対して、比較 \(\mathit{dist}(v) > \mathit{dist}(u) + 1\) は最大でも一回しか実行されない。

これらの観察をまとめると、幅優先探索の実行時間が \(\pmb{O(V+E)}\) であると分かります。直感的に言えば、キューにある頂点はソース頂点 \(s\) から同じ速度で外側に向かって広がる波の波面です。この広がっていく波という比喩は 1961 年に Chin Yang Lee (チン・ヤン・リー) によって、Moore の Algorithm A を自身で実装、可視化したものを指して使われています。

また、"\(\text{if } \mathit{dist} (v) > \mathit{dist}(u) + 1\)" という条件を (明らかに) より単純な "\(\text{if } \mathit{dist}(v) = \infty\)" で置き換えることができることも分かります。他のグラフ走査アルゴリズムにおいて全ての頂点に一度だけ訪れることを保証する "印" の役割を、このアルゴリズムでは距離が果たすことになります。つまり頂点にラベル付けされた距離が有限ならばその頂点には "印が付いて" います。

図 8.6

有向グラフに対する幅優先探索の完全な実行例。キューから出てくる頂点の順番は \(s \bigstar b d \bigstar c a g \bigstar f e \bigstar h \bigstar \bigstar\) である (\(\bigstar\) がフェーズの終わりを表す)。強調された頂点がキューに入っている頂点を、青くて太い辺が成長している最小路木を表す。

しかし、最終的な距離のラベルが正しいことには証明が必要です！

定理 8.2 \(\textsc{BFS}\) が終わったとき、任意の頂点 \(v\) について、\(\mathit{dist}(v)\) は \(G\) における \(s\) から \(v\) までの最短路の長さを表す。

証明適当な頂点 \(v\) を固定し、\(G\) における任意の路 \(s = v_{0} \rightarrow\) \(v_{1} \rightarrow\) \(\cdots \rightarrow\) \(v_{l} = v\) を考える。任意の添え字 \(j\) に対して \(\mathit{dist}(v_{j}) \leq j\) であり、したがって \(\mathit{dist}(v) \leq l\) であることを示す。\(j\) に関する帰納法を使う。

\(\mathit{dist}(v_{0}) = \mathit{dist}(s) = 0\) は明らか。
任意の添え字 \(j > 0\) について、帰納法の仮定より \(\mathit{dist}(v_{j-1}) \leq j - 1\) である。キューから \(v_{j-1}\) を \(\textsc{Pull}\) したとき、\(\mathit{dist}(v_{j}) \leq \mathit{dist}(v_{j-1}) + 1\) が最初から成り立っているか、そうでなければ \(\mathit{dist}(v_{j}) \leftarrow \mathit{dist}(v_{j-1}) + 1\) という代入が実行される。いずれにせよ \(\mathit{dist}(v_{j}) \leq \mathit{dist}(v_{j-1}) + 1 \leq j\) が成り立つ。

\(\mathit{dist}(v)\) が最大でも \(s\) から \(v\) への任意の路の長さにしかならないことが示せたので、\(\mathit{dist}(v)\) は最大でも \(s\) から \(v\) への最短路の長さである。

同様の帰納法によって \(\mathit{dist}(v)\) が前者をたどった路 \(s \rightarrow\) \(\cdots \rightarrow\) \(\mathit{pred}(\mathit{pred}(v)) \rightarrow\) \(\mathit{pred}(v) \rightarrow v\) の長さと等しいことが分かるので、この路が最小路である。 \(\Box\)

Moore を動機付けたのは、Claude Shannon (クロード・シャノン) が 1950 年に設計・作成した迷路を解くロボット「テセウス (Theseus)」の弱点でした (テセウスは電気機械式のリレーで実装されたメモ化付きの深さ優先探索を使っていました。これがグラフにおける深さ優先探索の初めての実装であることはほぼ間違いないでしょう)。Moore によると: 「解が二つ以上ある迷路に対してこの機械を動かすのを見せると、ある訪問者が「なぜこの機械は最短路を答えないことがあるのか」と聞いてきた。そこで Shannon と私はこの問題を機械で解く安価な方法を研究した。彼はアナログ計算に適した方法をいくつか見つけ、私はこれらのアルゴリズムを思いついた」²^[return]
迷路を通り抜ける最短路を見つけるアナログな方法として提案されたものには、ボールベアリング、液体/プラズマの流れ、化学反応の波、走化性、レジスタネットワーク、LED の付いた電子回路、メモリスタのネットワーク、マイクロ流体力学チップ内のグロー放電、植物の育成、粘菌、アメーバ、アリ、蜂、線虫、そして観光客があります。^[return]
Konrad Zuse は初期のコンピューティングのパイオニアの一人です。 1930 年代後半、彼は (後に Z1 と名付けられる) 自身初のプログラム可能なコンピューターを両親のリビングルームにおいてあった金属の棒とストリップから作成しました。しかしオリジナルの Z1 とその設計図は 1944 年の英国の空襲によって破壊されてしまいます。Zuse の 1945 年の博士論文には Plankalkül (プランカルキュール) と呼ばれる世界初の高レベルプログラミング言語が示されています。Zuse の博士論文に含まれる Plankalkül プログラムの最初の完全な例は幅優先探索を使ってグラフの成分を数える処理の実装であり、疑似コードによる説明と 8 頂点の非連結グラフに対するアルゴリズムの実行例がステップごとに図示されています。ナチス政権が崩壊したために Zuse は博士論文を提出できず、 Plankalkül は 1972 年まで公表されませんでした。Plankalkül の初の実装が Joachim Hohmann (ヨアキム・ホーマン) によって発表されたのはようやく 1975 年のことです。^[return]