§220 対数関数の定義
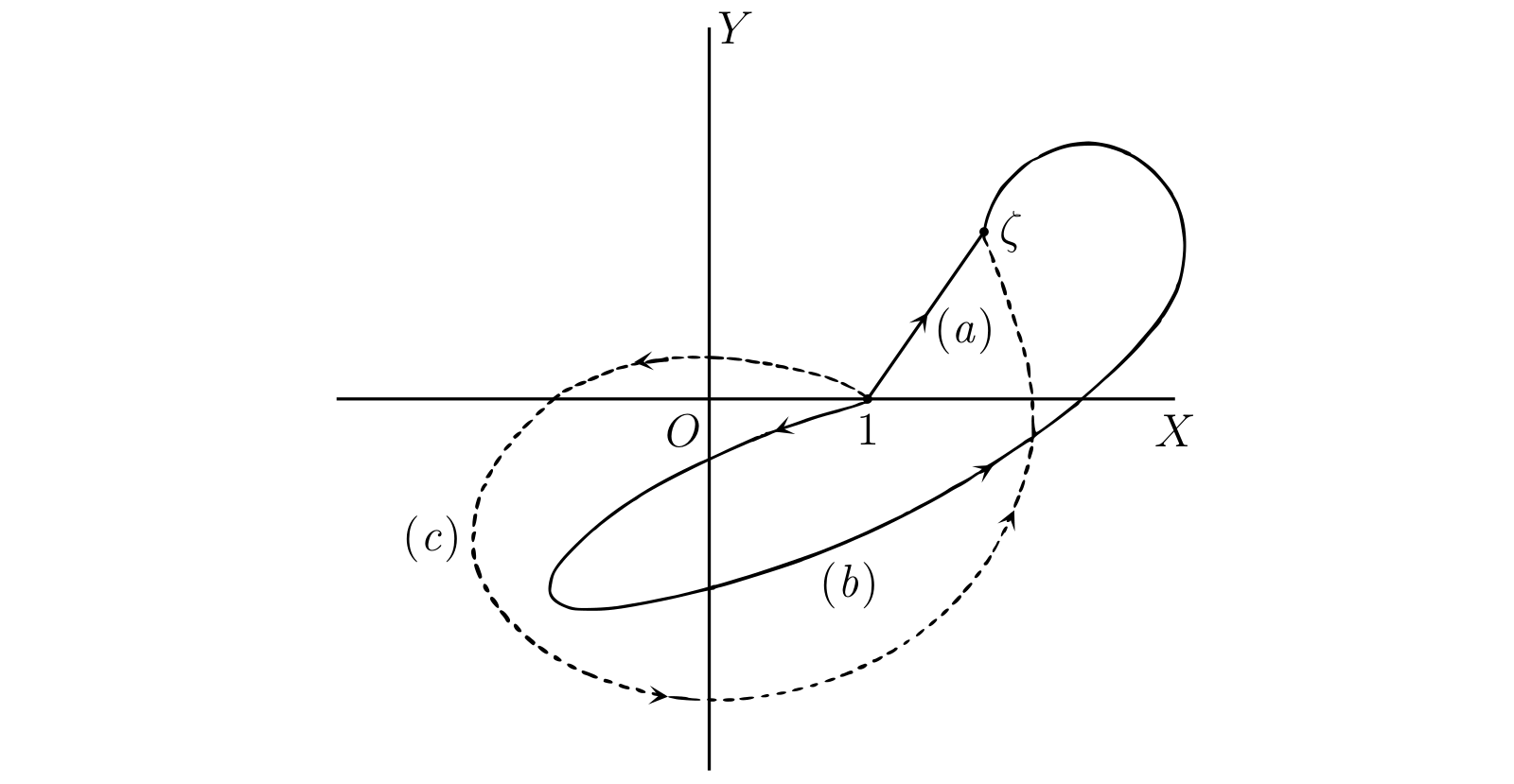
\(\zeta = \xi + i\eta\) を任意の複素数とする。一般的な \(\zeta\) の対数 \(\operatorname{Log} \zeta\) を次の等式で定義する: \[ \operatorname{Log} \zeta = \int_{C} \frac{dz}{z} \] ここで \(C\) は \(1\) から始まって \(\zeta\) で終わる、原点を通らない曲線とする。例えば 図 54 の \((a),\ (b),\ (c)\) はどれもこの積分路として利用できる。\(\operatorname{Log} z\) の値は特定の積分路が選ばれたときに定義されるが、今の段階では、こうして定義される \(\operatorname{Log} z\) の値が選ばれる積分路によってどう変化するかは明らかでない。例えば \(\zeta\) が正の実数 \(\xi\) のとき、考えられる積分路の一つとして \(1\) から \(\xi\) への直線がある。方程式 \(x = t,\ y = 0\) で定義されるこの積分路を考えたときの積分は \[ \operatorname{Log} \xi = \int_{1}^{\xi} \frac{dt}{t} \] であり、前章で定義した実数 \(\xi\) の対数 \(\log \xi\) に等しい。つまり \(\xi\) が正の実数なら、\(\operatorname{Log} \xi\) の値の一つが \(\log \xi\) となる。しかしこのとき、そして一般に、積分路には無数の選択肢がある。全ての \(\operatorname{Log} \xi\) が \(\log \xi\) に等しい証拠はなく、後で見るように実際のところ等しくない。表記を \(\log \zeta\) や \(\log \xi\) ではなく \(\operatorname{Log} \zeta\) および \(\operatorname{Log} \xi\) としたのはこのためである。\(\operatorname{Log} \xi\) は多値 (の可能性がある) 関数であり、\(\log \xi\) はその値の一つに過ぎない。今の私たちが持っている知識で考えるとき、一般の \(\operatorname{Log} \zeta\) の値について次の三つの可能性がある:
- \(1\) から \(\zeta\) へのどの路を選んでも同じになる。
- 全ての異なる路に対して異なる値が得られる。
- 特定の路のクラスごとに対応する値が存在する。
これらのどれが正しくどれが間違っているかは定義を見ても全く分からない。