§221 対数関数の値
点 \(z = \zeta\) の極座標が \((\rho, \phi)\) で \[ \zeta = \rho(\cos\phi + i\sin\phi) \] が成り立つとして、さらに \(-\pi \lt \phi \lt \pi\) で \(\rho\) は正とする。このとき \(\zeta\) は \(0\) と負の実数以外の全ての値を取る。
路 \(C\) における任意の点の座標 \((x, y)\) は \(t\) の関数であり、その極座標 \((r, \theta)\) も \(t\) の関数である。また §219 の定義からは \[ \operatorname{Log} \zeta = \int_{C} \frac{dz}{z} = \int_{C} \frac{dx + i\, dy}{x + iy} = \int_{t_{0}}^{t_{1}} \frac{1}{x + iy} \left(\frac{dx}{dt} + i\frac{dy}{dt}\right) dt \] が分かる。一方で \(x = r\cos\theta,\ y = r\sin\theta\) だから \[ \begin{aligned} \frac{dx}{dt} + i\frac{dy}{dt} & = \left(\cos\theta\, \frac{dr}{dt} - r\sin\theta\, \frac{d\theta}{dt}\right) + i\left(\sin\theta\, \frac{dr}{dt} + r\cos\theta\, \frac{d\theta}{dt}\right) \\ & = (\cos\theta + i\sin\theta) \left(\frac{dr}{dt} + ir\frac{d\theta}{dt}\right) \end{aligned} \] が成り立つ。よって \[ \operatorname{Log} \zeta = \int_{t_{0}}^{t_{1}} \frac{1}{r}\, \frac{dr}{dt}\, dt + i\int_{t_{0}}^{t_{1}} \frac{d\theta}{dt}\, dt = [\log r] + i[\theta] \] である。ここで \([\log r]\) は \(t = t_{1}\) と \(t = t_{0}\) に対応する点における \(\log r\) の値の差を表し、\([\theta]\) も同様とする。
実部 \([\log r]\) に関しては \[ [\log r] = \log \rho - \log 1 = \log \rho \] が明らかに分かる。しかし虚部 \([\theta]\) についてはさらに議論が必要となる。まず積分路が \(1\) と \(\zeta\) を結ぶ直線の場合を考える。最初の \(\theta\) の値は \(1\) の偏角、正確には \(1\) の偏角の一つであり、整数 \(k\) を使って \(2k\pi\) と表せる。最初の値を \(\theta = 2k\pi\) としよう。すると \(t\) が直線上を移動するとき、\(\theta\) は \(2k\pi\) から \(2k\pi + \phi\) に増加する。よって \[ [\theta] = (2k\pi + \phi) - 2k\pi = \phi \] となる。つまり積分路が直線なら \(\operatorname{Log} \zeta = \log \rho + i\phi\) が成り立つ。

この \(\operatorname{Log} \zeta\) の値を主値 (principal value) と呼ぶ。\(\zeta = \rho\) かつ \(\phi = 0\) で \(\zeta\) が正の実数なら \(\operatorname{Log} \zeta\) の主値は通常の \(\log \zeta\) に等しいので、\(\operatorname{Log} \zeta\) の主値を \(\log \zeta\) と表記すれば一貫性が保たれる。よって \[ \log \zeta = \log \rho + i\phi \] と定めるのが理にかなっている。主値は虚部 \(\phi\) が \(-\pi\) と \(\pi\) の間にあるという事実によって特徴付けられる。
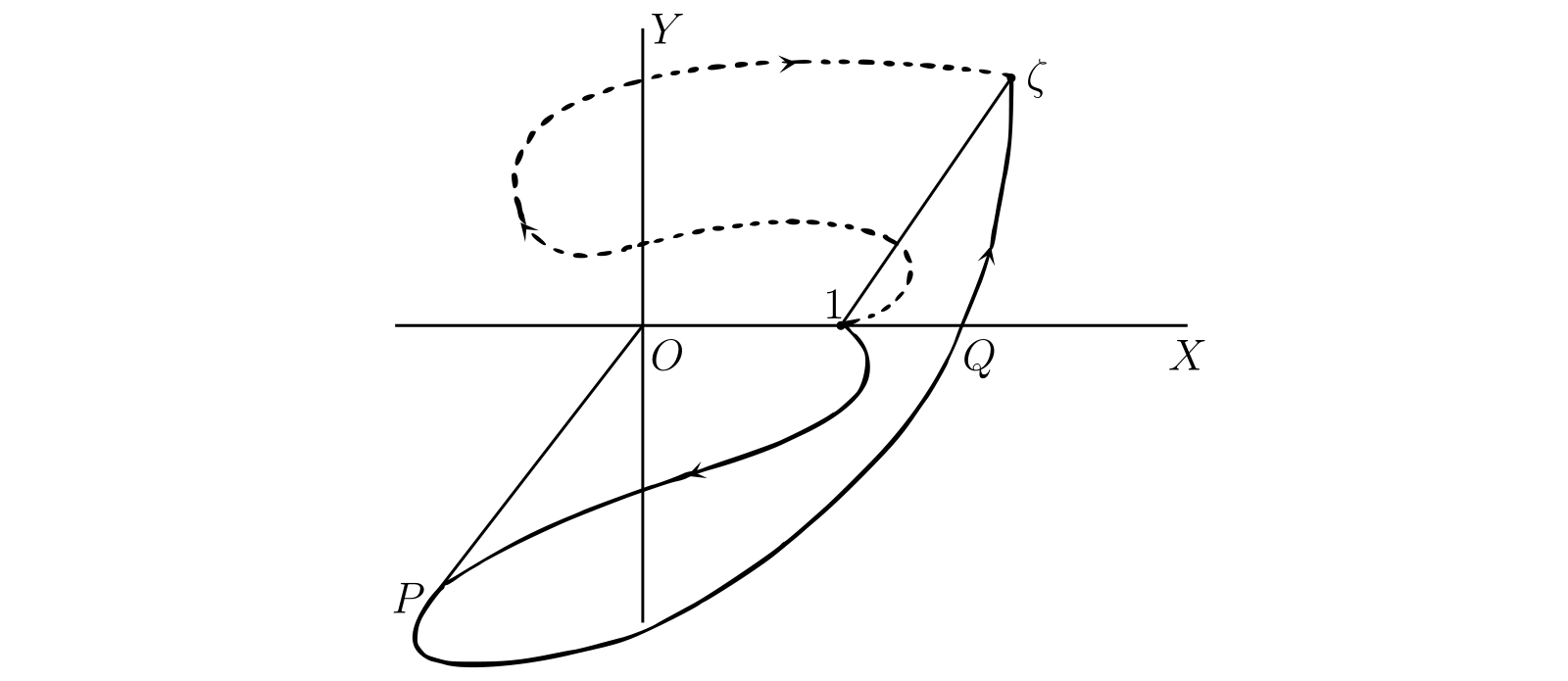
続いて 図 56 のように、\(1\) と \(\zeta\) を結ぶ直線と積分路が囲む領域が原点を含まない場合を考える。\([\theta]\) がこの場合にも \(\phi\) に等しいことは容易に分かる。例えば図中の実線で書かれた積分路では、最初 \(2k\pi\) に等しい \(\theta\) はまず \[ 2k\pi - \angle XOP \] まで減少し、それから増加する。\(\theta\) は点 \(Q\) で \(2k\pi\) に等しくなり、最終的に \(2k\pi + \phi\) となる。破線の積分路では多少複雑になるが、結論は変わらない。ここでは直線と曲線が二つの領域を囲むが、原点は含まない。つまり \(\bm{1}\) と \(\bm{\xi}\) を結んだ直線と積分路からなる閉曲線が原点を含まないなら \[ \bm{\operatorname{Log} \zeta = \log \zeta = \log \rho + i\phi} \] が成り立つ。
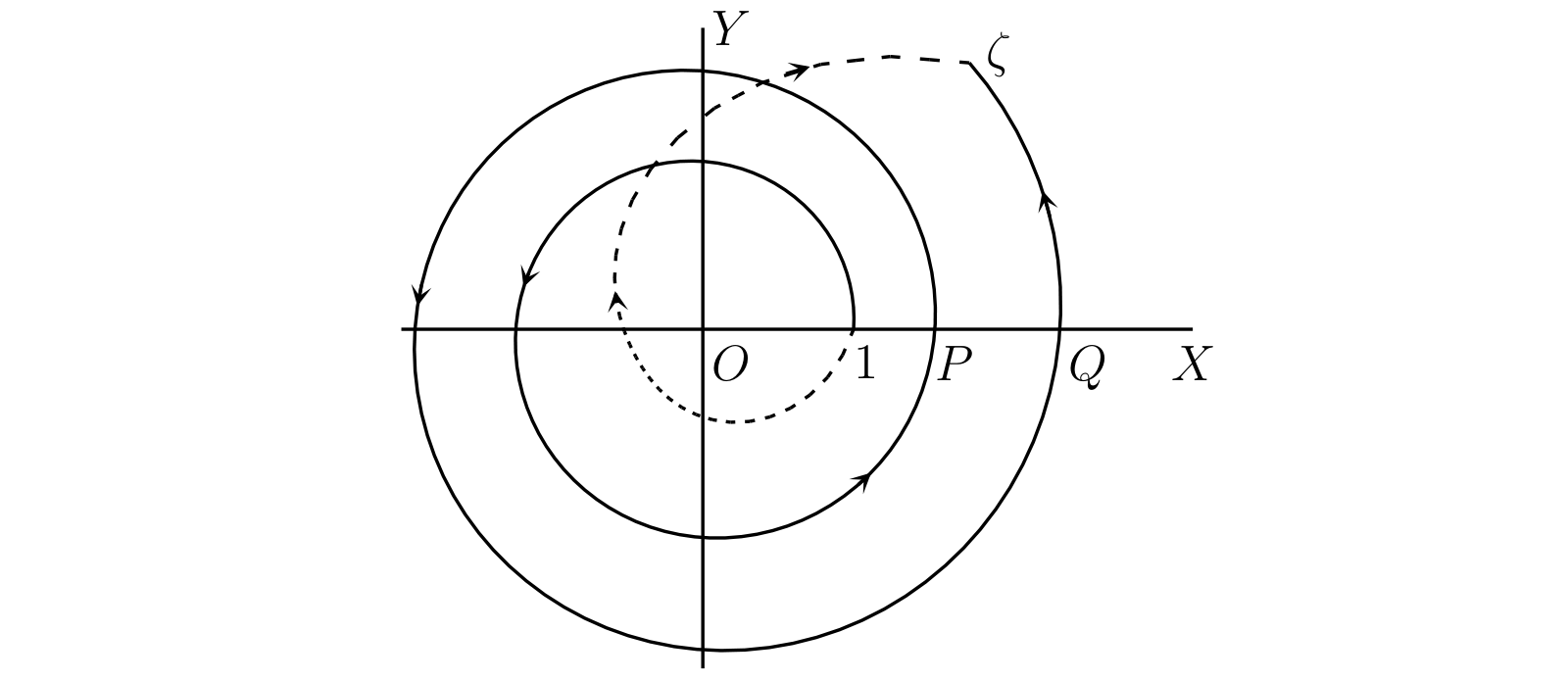
一方で \([\theta]\) が \(\phi\) と等しくならない積分路も簡単に構成できる。例として 図 57 中の実線で示される曲線を考える。\(\theta\) が最初 \(2k\pi\) に等しいとすれば、\(\theta\) は \(P\) に着くまでに \(2\pi\) 増加し、\(Q\) に着くまでに \(4\pi\) 増加する。最終的な \(\theta\) の値は \(2k\pi + 4\pi + \phi\) であり、\([\theta] = 4\pi + \phi\) が得られる。つまりこの積分路を使うと \[ \operatorname{Log} \zeta = \log \rho + i(4\pi + \phi) \] となる。
この場合には積分路が原点の周りを正方向に二回周回する。原点の周りを \(k\) 回周回する路が積分路なら、全く同じ議論によって \([\theta] = 2k\pi+ \phi\) つまり \[ \operatorname{Log} \zeta = \log \rho + i(2k\pi + \phi) \] が分かる。またこの等式で \(k\) は正となっているが、図 57 の破線ように原点の周りを逆方向に周回する積分路を考えれば \(k\) を負とした値も全て得られる。\(|\zeta| = \rho\) で \(2k\pi + \phi\) は \(\arg \zeta\) の異なる値だから、\(\log |\zeta| + i\arg \zeta\) の全ての値が \(\operatorname{Log} \zeta\) だと結論できる。さらにここまでの議論から、\(\operatorname{Log} \zeta\) の全ての値がこの形だとも分かる。
以上を次にまとめる:
\(\operatorname{Log} \zeta\) の一般的な値は \[ \log |\zeta| + i\arg \zeta = \log \rho + i(2k\pi + \phi) \] である。ここで \(k\) は正または負の整数を表し、その値は積分路によって決定される。積分路が直線なら \(k = 0\) であり、次が成り立つ: \[ \operatorname{Log} \zeta = \log \zeta = \log \rho + i\phi \]
ここまでの議論では \(\zeta\) が関数 \(\operatorname{Log}\) の引数で、\((\xi, \eta)\) と \((\rho, \phi)\) が \(\zeta\) の座標、\(z\) が積分路上の点、\((x, y)\) と \((r, \theta)\) が \(z\) の座標としてきた。しかし \(\operatorname{Log}\) の引数を通常通り \(z\) で表してはいけない理由はないため、次の例からは \(\operatorname{Log} z\) を使うことにする。
-
上の議論では \(-\pi \lt \theta \lt \pi\) を仮定したので、\(z\) が負の実数の場合は除かれていた。\(z\) が負の実数だと \(1\) と \(z\) を結ぶ直線が \(0\) を通るために、この直線を積分路とした積分を計算できない。\(\pi\) と \(-\pi\) はどちらも \(\arg z\) で \(\theta\) はどちらかと等しい。また \(r = -z\) である。この場合でも \(\operatorname{Log} z\) は \(\log |z| + i\arg z\) に等しく、整数 \(k\) を使って \[ \log (-z) + (2k + 1)\pi i \] と表せる。\(\log (-z) + \pi i\) と \(\log (-z) - \pi i\) という値はそれぞれ \(1\) と \(z\) を結ぶ積分路であって常に \(x\) 軸より上および下にあるものに対応する。都合に応じてどちらでも \(\operatorname{Log} z\) の主値とみなすことができる。本書では \(x\) 軸よりも上を通る積分路に対応する \(\log (-z) + i\pi\) を主値として採用する。
-
\(\operatorname{Log} z\) の任意の値の実部および虚部は \(x\) と \(y\) の連続関数である。ただし \(x = 0,\ y = 0\) は除く。
-
\(\bm{\operatorname{Log} z}\) の満たす関数方程式: 関数 \(\operatorname{Log} z\) は次の方程式を満たす: \[ \operatorname{Log} z_{1} z_{2} = \operatorname{Log} z_{1} + \operatorname{Log} z_{2} \qquad \text{(1)} \] この等式は左辺または右辺の全ての値がもう一方のある値に等しくなるという意味で成り立つ。証明は \[ z_{1} = r_{1}(\cos\theta_{1} + i\sin\theta_{1}),\quad z_{2} = r_{2}(\cos\theta_{2} + i\sin\theta_{2}) \] とおいて §221 の結果を使う。ただし \[ \log z_{1}z_{2} = \log z_{1} + \log z_{2} \qquad \text{(2)} \] が常に成り立つとは限らない。例えば \[ z_{1} = z_{2} = \dfrac{1}{2}(-1 + i\sqrt{3}) = \cos \dfrac{2}{3}\pi + i \sin \dfrac{2}{3}\pi \] のとき \(\log z_{1} = \log z_{2} = \frac{2}{3}\pi i\) および \(\log z_{1} + \log z_{2} = \frac{4}{3}\pi i\) だが、\(\frac{4}{3}\pi i\) は \(\operatorname{Log} z_{1}z_{2}\) の値の一つであるものの主値ではない。主値は \(\log z_{1}z_{2} = -\frac{2}{3}\pi i\) である。
\(\text{(1)}\) のように片側の全ての値がもう一方のとある値になり、その逆も成り立つ等式を完全な等式 (complete equation) あるいは完全に正しい (completely true) 等式と呼ぶ。
-
整数 \(m\) に対する等式 \(\operatorname{Log} z^{m} = m\operatorname{Log} z\) は完全には正しくない。右辺の値は全て左辺のとある値となるが、逆は正しくない。
-
等式 \(\operatorname{Log} (1/z) = -\operatorname{Log} z\) は完全に正しい。また \(z\) が負の実数でなければ \(\log (1/z) = -\log z\) も成り立つ。
-
等式 \[ \log \left(\frac{z - a}{z - b}\right) = \log (z - a) - \log (z - b) \] が正しくなるのは、点 \(z = a\) と \(z = b\) を結ぶ直線と、これらの点を通り \(x\) 軸負方向に無限に延びる二直線によって囲まれる領域の外側に \(z\) があるときである。
-
等式 \[ \log \left(\frac{a - z}{b - z}\right) = \log \left(1 - \frac{a}{z}\right) - \log \left(1 - \frac{b}{z}\right) \] は \(z\) が三点 \(O,\ a,\ b\) からなる三角形の外側にあるとき正しい。
-
実数変数 \(x\) の関数 \(\operatorname{Im}(\operatorname{Log} x)\) のグラフを描け。 [このグラフは \(y = 2k\pi\) の正の部分と \(y = (2k + 1)\pi\) の負の部分からなる]
-
等式 \[ \pi f(x) = p\pi + (q - p)\operatorname{Im}(\log x) \] で定義される実変数 \(x\) の関数 \(f(x)\) は \(x\) が正のとき \(p\) に等しく、\(x\) が負のとき \(q\) に等しい。
-
等式 \[ \pi f(x) = p\pi + (q - p)\operatorname{Im}\{\log(x - 1)\} + (r - q)\operatorname{Im}(\log x) \] で定義される関数 \(f(x)\) は \(x \gt 1\) で \(p\) に等しく、\(0 \lt x \lt 1\) で \(q\) に等しく、\(x \lt 0\) で \(r\) に等しい。
-
(i) \(\log z\) と (ii) \(\operatorname{Log} z\) の値が (a) 実数あるいは (b) 純虚数になる \(z\) の値はそれぞれ何か?
-
\(z = x + iy\) なら \(\operatorname{Log}\operatorname{Log} z = \log R + i(\Theta + 2k'\pi)\) が成り立つ。ここで \[ R^{2} = (\log r)^{2} + (\theta + 2k\pi)^{2} \] であり、\(\Theta\) は次の等式を満たす最小の正の角度である: \[ \cos\Theta : \sin\Theta : 1 = \log r : \theta + 2k\pi: \sqrt{(\log r)^{2} + (\theta + 2k\pi)^{2}} \] 二重に無限に存在する \(\operatorname{Log}\operatorname{Log}(1 + i\sqrt{3})\) を大まかにプロットせよ。\(\log\operatorname{Log}(1 + i \sqrt{3})\) と \(\operatorname{Log}\log(1 + i\sqrt{3})\) がどれに対応するか示せ。