§151 平面曲線の交点

ある点が二つの曲線の両方に存在するとき、二つの曲線はその点で交わる (intersect) と言う。さらにその点における接線が同じなら、二つの曲線はその点で接する (touch) と言う。

二つの関数 \(f(x)\) と \(\phi(x)\) について、全ての次数の導関数が \(x = \xi\) で連続とする。曲線 \(y = f(x)\) と \(y = \phi(x)\) を考える。一般に \(f(\xi)\) と \(\phi(\xi)\) は異なっており、\(x = \xi\) という横座標は交点に対応しない。しかしもし \(f(\xi) = \phi(\xi)\) なら、\(x = \xi,\ y = f(\xi) = \phi(\xi)\) という点で曲線が交わる。二つの曲線がこの点で交わるとする。さらに曲線がこの点で接するには、一次導関数 \(f'(x)\) と \(\phi'(x)\) が \(x = \xi\) で等しいことが必要十分である。

図 45

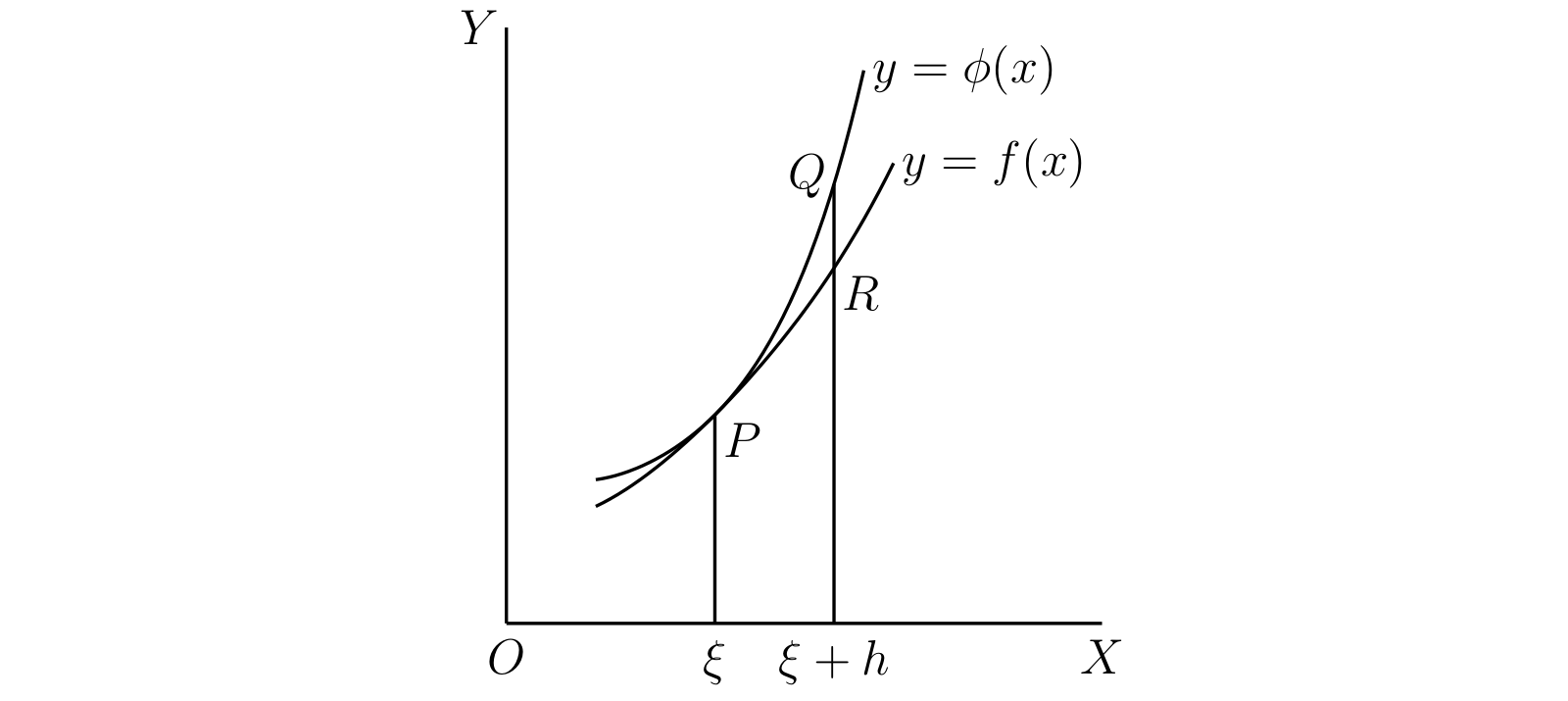
曲線が接触する点は異なる視点からも観察できる。上図では二つの曲線が \(P\) で接しており、\(QR\) が \(\phi(\xi + h) - f(\xi + h)\) に等しい。\(\phi(\xi) = f(\xi)\) および \(\phi'(\xi) = f'(\xi)\) だから、\(QR\) は \[ \dfrac{1}{2} h^{2}\{\phi''(\xi + \theta h) - f''(\xi + \theta h)\} \] にも等しい。ここで \(\theta\) は \(0\) から \(1\) の間の実数を表す。ここから \(h \to 0\) で \[ \lim \frac{QR}{h^{2}} = \dfrac{1}{2}\{\phi''(\xi) - f''(\xi)\} \] だと分かる。言い換えると、\(x\) 座標が \(\xi\) の点で二つの曲線が接するなら、\(\bm{x}\) 座標が \(\bm{\xi + h}\) の点における曲線の \(\bm{y}\) 座標の差は \(\bm{h}\) が小さいとき二次の小ささを持つ。

簡単に分かるように、曲線が交わるが接しはしないとき \(\lim (QR/h) = \phi'(\xi) - f'(\xi)\) が成り立ち、\(QR\) は一次の小ささを持つ。

つまり \(QR\) の小ささの次数を曲線の接触点の近さの指標として採用できる。つまり \(f\) と \(\phi\) の \(n - 1\) 次までの導関数が \(x = \xi\) で同じ値を取るなら、\(QR\) は \(n\) 次の小ささを持つ。この事実および次の式を示すのは難しくない: \[ \lim \frac{QR}{h^{n}} = \frac{1}{n!}\{\phi^{(n)}(\xi) - f^{(n)}(\xi)\} \] よって次の定義が得られる:

\(f(\xi) = \phi(\xi),\ f'(\xi) = \phi'(\xi),\ \ldots,f^{(n)}(\xi) = \phi^{(n)}(\xi)\) および \(f^{(n+1)}(\xi) \neq \phi^{(n+1)}(\xi)\) なら、曲線 \(y = f(x)\) と \(y = \phi(x)\) の \(x\) 座標が \(\xi\) の点を \(n\) 次の接触点 (contact of the \(n\)th order) と呼ぶ。

\(n\) 次の接触点に関するここまでの議論は軸の取り方に依存しており、接線が \(y\) 軸と平行なときには行えない。\(y\) が独立変数で \(x\) が従属変数だとみなせばこの場合を扱えるが、\(x\) と \(y\) の両方をパラメータ \(t\) の関数とみなした方が分かりやすい。この理論の素晴らしい解説が §147 で示したフォウラー氏による文献およびド・ラ・ヴァレ・プーサン著 Cours d'Analyse, vol. ii, pp. 396 et seq. にある。

例 59

  1. \(\phi(x) = ax + b\) なら \(y = \phi(x)\) は直線となる。\(x = \xi\) の点が接点となる条件は \(f(\xi) = a\xi + b\) かつ \(f'(\xi) = a\) である。この条件が満たされる \(a\) と \(b\) を計算すれば \(a = f'(\xi)\) と \(b = f(\xi) - \xi f'(\xi)\) を得る。よって \(x = \xi\) における \(y = f(x)\) の接線の方程式は \[ y = xf'(\xi) + \{f(\xi) - \xi f'(\xi)\} \] つまり \(y - f(\xi) = (x - \xi)f'(\xi)\) となる (参考: 例 39.5)。

  2. 曲線上の点で接する直線は一意に決定される。接線と曲線が二次の接触点を持つには、\(f''(\xi) = \phi''(\xi)\) つまり \(f''(\xi) = 0\) でなければならない。曲線の接線が二次の接触点を持つ点を変曲点 (point of inflexion) と呼ぶ。

  3. 次の関数の変曲点を求めよ: \[ 3x^{4} - 6x^{3} + 1,\quad \dfrac{2x}{1 + x^{2}},\quad \sin x,\quad a\cos^{2}x + b\sin^{2}x,\quad \tan x,\quad \arctan x \]

  4. 円錐曲線 \(ax^{2} + 2hxy + by^{2} + 2gx + 2fy + c = 0\) が変曲点を持たないことを示せ。 [添え字で微分を表せば \(ax + hy + g + (hx + by + f)y_{1} = 0\) および \[ a + 2hy_{1} + by_{1}^{2} + (hx + by + f)y_{2} = 0 \] が成り立つ。よって変曲点において \[ a + 2hy_{1} + by_{1}^{2} = 0 \] が分かる。ここから \[ a(hx + by + f)^{2} - 2h(ax + hy + g)(hx + by + f) + b(ax + hy + g)^{2} = 0 \] つまり \[ (ab - h^{2})\{ax^{2} + 2hxy + by^{2} + 2gx + 2fy\} + af^{2} - 2fgh + bg^{2} = 0 \] となる。しかしこれが成り立つのは、円錐曲線の方程式が \[ af^{2} - 2fgh + bg^{2} = c(ab - h^{2}) \] つまり \(abc + 2fgh - af^{2} - bg^{2} - ch^{2} = 0\) を満たすときに限られる。これは円錐曲線が二つの直線に退化するための条件である]

  5. \(y = \dfrac{ax^{2} + 2bx + c}{\alpha x^{2} + 2\beta x + \gamma}\) は \(\alpha x^{2} + 2\beta x + \gamma = 0\) が実根を持つなら一つの変曲点を、虚根を持つなら三つの変曲点を持つ。

    [原点を変更することで、この方程式で表される曲線は次の形に変形できる (参考: 例 46.15): \[ \eta = \frac{\xi}{A\xi^{2} + 2B\xi + C} = \frac{\xi}{A(\xi - p)(\xi - q)} \] \(p\) と \(q\) は実数または複素数を表す。変曲点の条件は \(\xi^{3} - 3pq\xi + pq(p + q) = 0\) となる。これは \(\{pq(p - q)\}^{2}\) の正負に応じて一つまたは三つの実根を持つ。つまり \(p\) と \(q\) が実数か複素数かに応じて変曲点の数が変化する]

  6. 具体的な曲線 \(y = \dfrac{1 - x}{1 + x^{2}},\ y = \dfrac{1 - x^{2}}{1 + x^{2}},\ y = \dfrac{1 + x^{2}}{1 - x^{2}}\) の変曲点について議論せよ。

  7. 問題 5 の曲線が三つの変曲点を持つとき、それらが一直線上にあることを示せ。 [方程式 \(\xi^{3} - 3pq\xi + pq(p + q) = 0\) は \((\xi - p)(\xi - q)(\xi + p + q) + (p - q)^{2}\xi = 0\) と変形できる。すなわち、変曲点は直線 \(\xi + A(p - q)^{2}\eta + p + q = 0\) つまり \(A\xi - 4(AC - B^{2})\eta = 2B\) 上にある]

  8. 曲線 \(y = x\sin x\) と \(y = \dfrac{\sin x}{x}\) が無限に多くの変曲点を持つと示せ。

  9. 曲線の接触点と曲率1: 一般的な円の方程式 \[ (x - a)^{2} + (y - b)^{2} = r^{2} \qquad \text{(1)} \] には任意定数が三つ含まれる。この定数を、円と曲線 \(y = f(x)\) の接触点 \((\xi, \eta)\) がなるべく高い次数になるように定める問題を考える。ここで \(\eta = f(\xi)\) として、\(f'(\xi)\) と \(f''(\xi)\) を \(\eta_{1}\) および \(\eta_{2}\) と書く。円の方程式を二回微分すると \[ (x - a) + (y - b)y_{1} = 0, \qquad \text{(2)} \] \[ 1 + y_{1}^{2} + (y - b)y_{2} = 0 \qquad \text{(3)} \] が分かる。

    もし円が曲線と接するなら、\(\text{(1)}\) と \(\text{(2)}\) が \(x = \xi,\ y = \eta,\ y_{1} = \eta_{1}\) で満たされる。ここから \((\xi - a)/\eta_{1} = -(\eta - b) = r/\sqrt{1 + \eta_{1}^{2}}\) が分かる。もし接触点が二次なら加えて \(\text{(3)}\) も成り立つ。このとき \(b = \eta + \{(1 + \eta_{1}^{2})/\eta_{2}\}\) であり、まとめると \[ a = \xi - \frac{\eta_{1}(1 + \eta_{1}^{2})}{\eta_{2}},\quad b = \eta + \frac{1 + \eta_{1}^{2}}{\eta_{2}},\quad r = \frac{(1 + \eta_{1}^{2})^{3/2}}{\eta_{2}} \] となる。

    曲線との二次の接触点 \((\xi, \eta)\) を持つ円を曲率円 (circle of curvature) と呼び、曲率円の半径を曲率半径 (radius of curvature)、曲率半径の逆数を曲率 (curvature) と呼ぶ。つまり曲率は \(f''(\xi)/\{1 + [f'(\xi)]^{2}\}^{3/2}\) すなわち \[ \frac{d^{2}\eta}{d\xi^{2}} \bigg/ \biggl\{1 + \biggl(\frac{d\eta}{d\xi}\biggr)^{2}\biggr\}^{3/2} \] に等しい。

  10. 円の曲率が一定であり、半径の逆数に等しいことを示せ。さらに曲率が一定の曲線は円に限ることを示せ。

  11. 円錐曲線 \(y^{2} = 4ax\) と \((x/a)^{2} + (y/b)^{2} = 1\) の曲率半径と曲率中心を求めよ。

  12. 楕円上の点 \(P\) における曲率半径は \(\dfrac{CD^{3}}{ab}\) である。\(CD\) は \(CP\) と共役な2半径の長さを表す。

  13. 曲線 \(y = f(x)\) 上の点 \(P\) が与えられたときに、\(y = f(x)\) と四次の接触点を持つ円錐曲線を描けることを一般的に示せ。

    [一般的な円錐曲線の方程式 \[ ax^{2} + 2hxy + by^{2} + 2gx + 2fy + c = 0 \] を \(x\) に関して四回微分する。添え字で微分の回数を表す記法を使うと \[ \begin{aligned} ax + hy + g + (hx + by + f) y_{1} & = 0,\\ a + 2hy_{1} + by_{1}^{2} + (hx + by + f) y_{2} & = 0,\\ 3(h + by_{1}) y_{2} + (hx + by + f) y_{3} & = 0,\\ 4(h + by_{1}) y_{3} +3by_{2}^{2} + (hx + by + f) y_{4} & = 0 \end{aligned} \] を得る。円錐曲線が四次の接触点を持つなら、この五つの等式が \(x,\ y,\ y_{1},\ y_{2},\ y_{3},\ y_{4}\) の値が \(\xi,\ \eta,\ \eta_{1},\ \eta_{2},\ \eta_{3},\ \eta_{4}\) のとき成り立つ。つまり比 \(a : b : c : f : g : h\) を求めるのにちょうど必要な数の等式が得られる]

  14. 曲線上の点 \(P\) と三次の接触点を持つ円錐曲線は無限に描ける。それらの中心が同一直線上にあることを示せ。

    [接線と法線を軸として取れば、円錐の方程式は \(2y = ax^{2} + 2hxy + by^{2}\) という形となる。\(x\) が小さいとき、\(y\) の値は第五章に関するその他の例 22より \[ y = \dfrac{1}{2}ax^{2} + \left(\dfrac{1}{2}ah + \varepsilon_{x}\right) x^{3} \] を満たす。ここで \(x \to 0\) のとき \(\varepsilon_{x} \to 0\) である。一方でこの式は \(x \to 0\) で \(\varepsilon'_{x} \to 0\) となる \(\varepsilon'_{x}\) を使った \[ y = \dfrac{1}{2}f''(0) x^{2} + \left(\dfrac{1}{6}f'''(0) + \varepsilon'_{x}\right) x^{3} \] と等しくなければならない。よって 例 55.15 から \(a = f''(0),\ h = \dfrac{f'''(0)}{3f''(0)}\) が分かる。そしてこの円錐曲線の中心は \(ax + hy = 0\) 上にある]

  15. 楕円 \((x/a)^{2} + (y/b)^{2} = 1\) の長軸の端と三次に接触する放物線を求めよ。

  16. 楕円 \((x/a)^{2} + (y/b)^{2} = 1\) 上の点 \((a\cos\alpha, b\sin\alpha)\) と三次に接触する円錐曲線の中心の軌跡は直径 \(x/(a\cos\alpha) = y/(b\sin\alpha)\) である。 [この楕円自身も条件を満たす円錐曲線であることから分かる]

  1. 曲率に関する詳細な解説は §147 で示したフォウラー氏による文献を参照。[return]

  2. 訳注: 楕円上の二点で引いた接線が直行するとき、中心とそれらの点を結んだ二つの半径を共役 (conjugate) であると言う。[return]

広告
このページの文章はテキストゆれないくんを使って校正されました。