§204 指数関数の定義
続いて全ての実数 \(y\) に対する指数関数 (exponential function) \(e^{y}\) を対数関数の逆関数として定義する。つまり \(y = \log x\) のとき \[ x = e^{y} \] と書く。
前に見たように、\(x\) が \(0\) から \(\infty\) に向かって変化すると \(y\) は \(-\infty\) から \(\infty\) へ狭義に単調増加する。よって一つの \(y\) の値には一つの \(x\) の値が対応し、その逆も成り立つ。同様に \(y\) は \(x\) の連続関数であり、§109 から \(x\) が \(y\) の連続関数だと分かる。
指数関数の連続性の直接的な証明は難しくない。\(x = e^{y}\) および \(x + \xi = e^{y + \eta}\) とすれば \[ \eta = \int_{x}^{x+\xi} \frac{dt}{t} \] だから、\(|\eta|\) は \(\xi \gt 0\) なら \(\xi/(x + \xi)\) より大きく、\(\xi \lt 0\) なら \(|\xi|/x\) より大きい。よって \(\eta\) が非常に小さいとき \(\xi\) も非常に小さくなる。
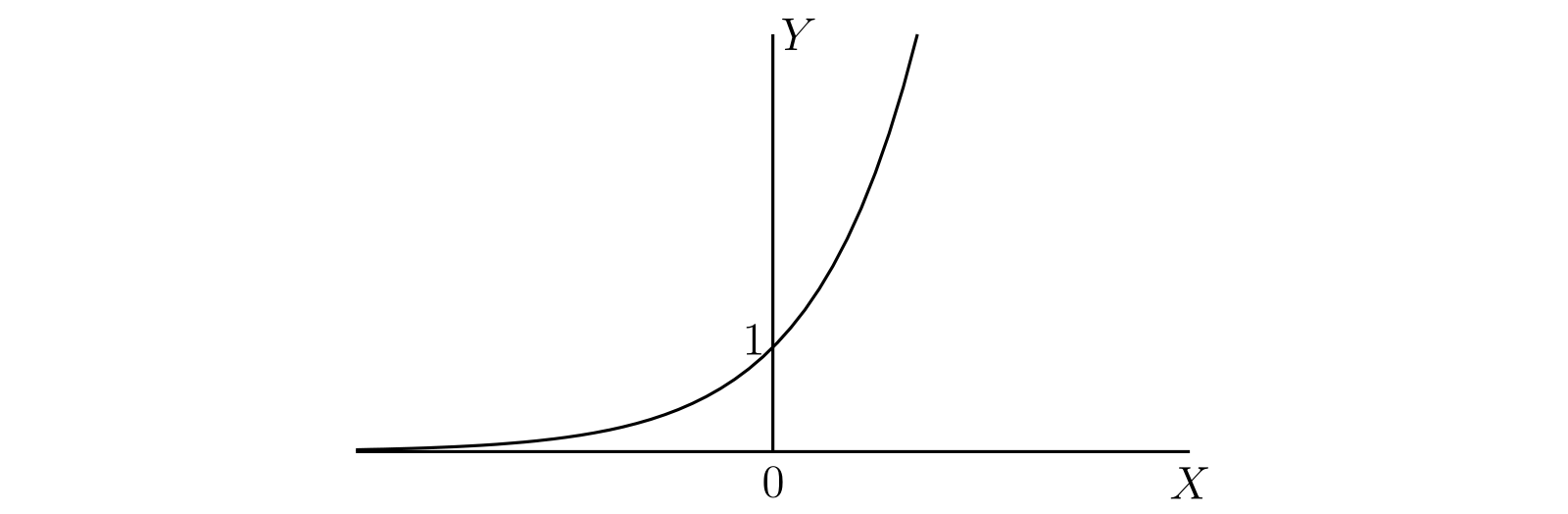
したがって \(e^{y}\) は \(y\) に関して連続で常に正な関数で、\(y\) が \(-\infty\) から \(\infty\) に変化するとき \(0\) から \(\infty\) へ単調に増加する。さらに \(y\) が有理数なら、\(e^{y}\) は \(e\) の初等的な意味での \(y\) 次の正のべきと等しくなる。\(e^{y}\) のグラフの概形を 図 53 に示す。