§39 複素数 (その 1)
\(OX\) に沿った変位 \([x]\) が点 \((x)\) と実数 \(x\) に対応したように、平面上の変位 \([x, y]\) にも対応する点 \((x, y)\) と実数の組 \(\bm{x,\ y}\) が存在する。
この実数の組 \(x,\ y\) を次のように表記すると便利である: \[ x + yi \] こう表記する理由は後で明らかになる。今は \(x + yi\) を \(\bm{[x, y]}\) の別表記に過ぎないと考えてなくてはならない。\(x + yi\) を複素数 (complex number) と呼ぶ。
次に複素数の同一性、加算、乗算を定義する。任意の複素数には対応する変位が一つ存在する。二つの複素数が同一なのは対応する変位が同一なときと定め、二つの複素数の和および積は対応する変位の和または積に対応する複素数と定める。つまり \[ x + yi = x' + y'i \qquad \text{(1)} \] は \(x = x',\ y = y'\) と同値であり、さらに次が成り立つ: \[ (x + yi) + (x' + y'i) = (x + x') + (y + y')i \qquad \text{(2)} \] \[ (x + yi) (x' + y'i) = xx' - yy' + (xy' + yx')i \qquad \text{(3)} \]
(2) と (3) の特殊ケースとして、次が成り立つ: \[ x + yi = (x + 0i) + (0 + yi) \] \[ (x + 0i) (x' + y'i) = xx' + xy'i \] この式は、複素数を扱うとき \(x + 0i\) の代わりに \(x\)、あるいは \(0 + yi\) の代わりに \(yi\) と書いても問題は起きないことを示している。これからは私たちもこう表記する。
複素数の整数乗と複素数の多項式は初等代数と同様に定義される。例えば (3) で \(x = x',\ y = y'\) とすれば次のようになる: \[ (x + yi)^{2} = (x + yi) (x + yi) = x^{2} - y^{2} + 2xyi \]
複素数の加算と乗算が次の式で表される代数法則を満たすことは簡単に確認できる: \[ \begin{aligned} (x + yi) + (x' + y'i) & = (x' + y'i) + (x + yi)\\ \{(x + yi) + (x' + y'i)\} + (x'' + y''i) & = (x + yi) + \{(x' + y'i) + (x'' + y''i)\}\\ (x + yi) (x' + y'i) & = (x' + y'i) (x + yi)\\ (x + yi)\{(x' + y'i) + (x'' + y''i)\} & = (x + yi)(x' + y'i) + (x + yi)(x'' + y''i)\\ \{(x + yi) + (x' + y'i)\}(x'' + y''i) & = (x + yi)(x'' + y''i) + (x' + y'i)(x'' + y''i)\\ (x + yi) \{(x' + y'i) (x'' + y''i)\} & = \{(x + yi) (x' + y'i)\} (x'' + y''i) \end{aligned} \] これらの証明は対応する変位に対する式の証明と本質的に同一である。
複素数の減算と除算は初等代数と同様に定義される。つまり \((x + yi) - (x' + y'i)\) の定義は \[ (x + yi) + \{- (x' + y'i)\} = x + yi + (-x' - y'i) = (x - x') + (y - y')i \] となる。あるいは次の式を満たす複素数 \(\xi + \eta i\) を定義としても構わない: \[ (x' + y'i) + (\xi + \eta i) = x + yi \] どちらを選んでも結果は変わらない。\((x + yi)/(x' + y'i)\) は次の式を満たす複素数 \(\xi + \eta i\) として定義される: \[ (x' + y'i) (\xi + \eta i) = x + yi \] 書き換えると \[ x' \xi - y' \eta + (x' \eta + y' \xi)i = x + yi \] となり、さらに変形すれば次の等式を得る: \[ x' \xi - y' \eta = x,\quad x' \eta + y' \xi = y \qquad \text{(4)} \]
この方程式を \(\xi\) と \(\eta\) について解くと \[ \xi = \frac{xx' + yy'}{{x'}^{2} + {y'}^{2}},\quad \eta = \frac{yx' - xy'}{{x'}^{2} + {y'}^{2}} \] が得られる。この解は \(x'\) と \(y'\) が両方 \(0\) のとき、つまり \(x' + y'i = 0\) のとき意味をなさない。そのため減算はいつでも行えるが、除算は割る数が \(0\) でないときのみ行える。
-
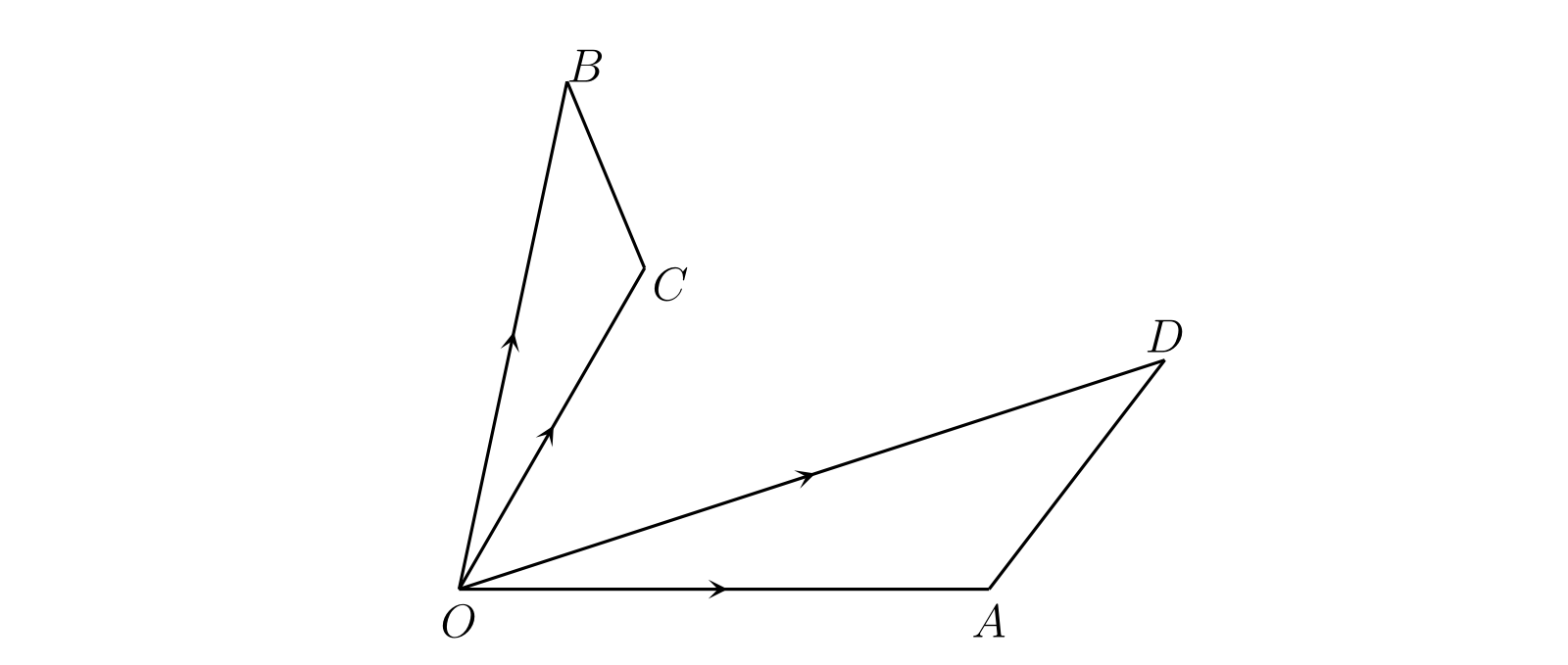
幾何学的に考えると、\(\overline{OB}\) を \(\overline{OC}\) で割る変位の除算は \(\triangle COB\) と \(\triangle AOD\) が相似になる \(D\) を見つける問題とみなせる。これは \(C\) が \(0\) と等しく \(\overline{OC} = 0\) である場合を除けば可能なことが示せる。
-
\(x + yi\) と \(x - yi\) は共役 (conjugate) であると言う。次の式を確認せよ: \[ (x + yi)(x - yi) = x^{2} + y^{2} \] つまり共役な二つの複素数の積は実数である。さらに次の式も示せ: \[ \begin{aligned} \frac{x + yi}{x' + y'i} & = \frac{(x + yi)(x' - y'i)}{(x' + y'i)(x' - y'i)} \\ & = \frac{xx' + yy' + (x'y - xy')i}{{x'}^{2} + {y'}^{2}} \end{aligned} \]