§98 実変数関数の連続性 (その 1)
読者は連続曲線 (continuousc curve) という言葉を意味をおおまかに理解していると思う。例えば 図 29 の \(C\) は連続で、\(C'\) は基本的に連続だが \(x = \xi'\) と \(x = \xi''\) で不連続となっている。
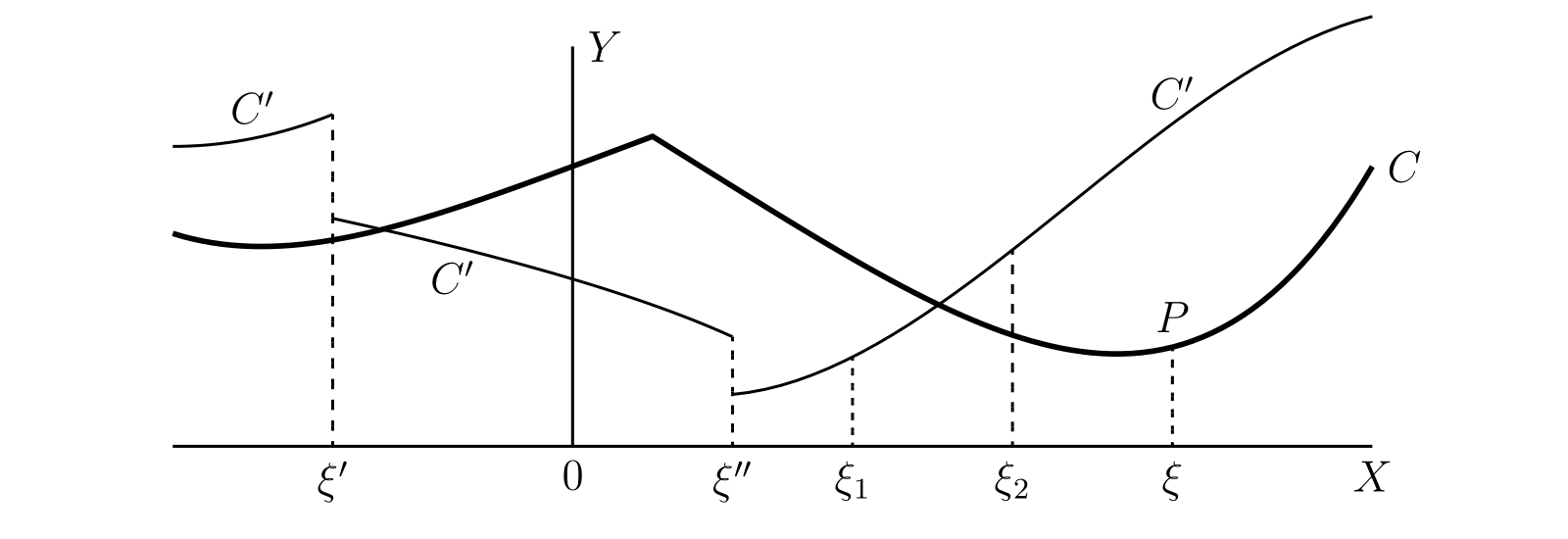
いずれにせよ任意の曲線は何らかの関数 \(\phi(x)\) のグラフとみなせる。とすれば、グラフが連続曲線となる関数を連続 (continuous) と呼び、そうでなければ不連続と呼ぶのが自然である。しばらくの間これが連続性の定義だとみなして、この性質から導かれる性質について詳しく見ていく。
まず曲線 \(C\) をグラフに持つ関数 \(y = \phi(x)\) の性質は、曲線上の各点が持つ性質から分かると言える。つまり全ての \(\bm{x}\) に対する連続性を定義するには、まずある点 \(\bm{x}\) に対する連続性を定義する必要がある。そこで \(x = \xi\) として \(x\) の値を固定して \(\xi\) に対応するグラフ上の点を \(P\) とする。この \(x\) の値に対応する \(\phi(x)\) が持つ特徴的な性質は何だろうか?
何よりもまず \(\bm{\phi(x)}\) が \(\bm{x = \xi}\) で定義される必要がある。これは明らかに必要であり、もし \(\phi(\xi)\) が定義されていないと曲線に穴が開いてしまう。
次に\(\bm{\phi(x)}\) が \(\bm{x = \xi}\) の近くの全ての \(\bm{x}\) で定義されている必要もある。言い換えると、全ての点で \(\phi(x)\) が定義されるような \(x = \xi\) を含んだ区間が存在しなければならない。
最後に \(\bm{x}\) が \(\bm{\xi}\) に近づくとき、左右どちらから近づいたとしても \(\bm{\phi(x)}\) が \(\bm{\phi(\xi)}\) に近づく必要がある。
私たちが常識的に連続曲線とみなすものが持っている性質はこれで全てではない。上述の三つの性質は直線や円といった特殊な曲線から一般化したものに過ぎない。しかしそれでも、これらは最も基礎的で最も単純な性質である。つまりこの三つの性質を持つ任意の関数のグラフは (実際に描ける限り) 私たちが連続曲線の見た目について抱く印象を持っている。そこでこの三つの性質が数学的な連続性の概念を表すとして、次の定義を得る:
\(\phi(x)\) が \(x = \xi\) で連続とは、\(x\) が \(\xi\) に向かうときの極限が両方の側について存在して、どちらの極限も \(\phi(x)\) に等しいことを言う。
次に区間内での連続性を定義する。とある \(x\) の区間内で \(\phi(x)\) が連続とは、区間内の全ての \(x\) で \(\phi(x)\) が連続なことを言う。また全ての \(x\) で \(\phi(x)\) が連続なら、\(\phi(x)\) は いたるところで連続 (continuous everywhere) と言う。例えば \([x]\) は \(\frac{1}{2}\) より小さい任意の正の実数 \(\delta\) に対する区間 \([\delta, 1 - \delta]\) で連続であり、\(1\) と \(x\) は両方ともいたるところで連続となる。
極限の定義に戻って書き直すと、連続性の定義は「\(\phi(x)\) が \(x = \xi\) で連続とは、\(\varepsilon \gt 0\) が与えられたときに、\(0 \leq |x - \xi| \leq \delta(\varepsilon)\) のとき \(|\phi(x) - \phi(\xi)| \lt \varepsilon\) となるよう \(\delta(\varepsilon)\) を選べることを言う」となる。
区間 \([a, b]\) でだけ定義される関数を考えることあるが、このときには点 \(a\) と \(b\) における連続性の定義を少しだけ変更する必要がある。つまり \(x = a\) では \(\phi(a + 0)\) が存在して \(\phi(x)\) に等しいこと、\(x = b\) では \(\phi(b - 0)\) が存在して \(\phi(b)\) に等しいことをもって連続と言う。