§100 連続関数の性質 (その 1)
§98 に示した連続性の概念が最も単純で最も自然なものとは思えないかもしれない。私たちが連続と言い表す概念を解析する方法をもう一つ示す。\(\phi(x)\) のグラフ上の点 \(A,\ B\) の座標をそれぞれ \((x_{0},\ \phi(x_{0})),\ (x_{1},\ \phi(x_{1}))\) とする。\(A\) と \(B\) の間を通る直線 \(\lambda\) を適当に取る。このとき常識的に考えると、連続な \(\phi(x)\) のグラフは \(\lambda\) を横切る。
この性質を連続曲線に固有の幾何学的性質とみなすなら、\(x\) 軸に平行な \(\lambda\) だけを考えたとしても一般性は失われないのは明らかである。ただ \(A\) と \(B\) の \(y\) 座標が同じになってはいけないので、議論の都合上 \(\phi(x_{1}) \gt \phi(x_{0})\) と仮定する。\(\lambda\) が直線 \(y = \eta\) で \(\phi_(x_{0}) \lt \eta \lt \phi(x_{1})\) を満たすなら、\(\phi(x)\) が \(\lambda\) を横切るとは、\(x_{0}\) と \(x_{1}\) の間にある \(x\) で \(\phi(x) = \eta\) が成り立つことを意味する。
つまり連続曲線 \(\phi(x)\) は次の性質を持たなければならないと結論できる: もし \[ \phi(x_{0}) = y_{0},\quad \phi(x_{1}) = y_{1} \] で \(y_{0} \lt \eta \lt y_{1}\) なら、\(\phi(x) = \eta\) を満たす \(x\) が \(x_{0}\) と \(x_{1}\) の間に存在する。言い換えると、\(x\) が \(x_{0}\) から \(x_{1}\) に動くときに、\(y\) が \(y_{0}\) から \(y_{1}\) までの全ての値を少なくとも一度ずつ取らなければならない。
§98 の意味で連続な \(x\) の関数 \(\phi(x)\) がこの性質を持つことを示そう。\(x_{0}\) の右側には \(\phi(x) \lt \eta\) が成り立つ \(x\) の区間が存在する: \(\phi(x) - \phi(x_{0}) \lt \eta - \phi(x_{0})\) なら \(\phi(x) \lt \eta\) だが、\(x = x_{0}\) で \(\phi(x)\) は連続なので \(x\) を \(x_{0}\) に十分近づければこの条件は成り立つ。同様に \(x_{1}\) の左側には \(\phi(x) \gt \eta\) が成り立つ \(x\) の区間がある。
\(x_{0}\) から \(x_{1}\) までの \(x\) を次のようにして二つのクラス \(L,\ R\) に分ける:
- クラス \(L\) には \(x_{0} \leq x \leq \xi\) を満たす全ての \(x\) で \(\phi(x) \lt \eta\) となる \(\xi\) を全て入れる。
- クラス \(R\) にはその他の \(x\) を全て入れる。つまり \(\phi(\xi) \geq \eta\) が成り立つか、\(x_{0}\) から \(\xi\) の間に \(\phi(x) \geq \eta\) となる \(x\) が存在する \(\xi\) を全て入れる。
すると \(L,\ R\) は §17 の定理の条件を満たすので、この組はとある実数の切断となる。この切断が表す実数を \(\xi_{0}\) とする。
まず \(\phi(\xi_{0}) \gt \eta\) と仮定する。このとき \(\xi_{0}\) は上クラスに含まれる。\(\xi_{0}\) より小さい全ての \(\xi'\) は \(L\) に含まれるので、\(\phi(\xi') \lt \eta\) が成り立つ。よって \(\phi(\xi_{0}) = \eta + k\) とすると \[ \phi(\xi_{0}) - \phi(\xi') \gt k \] となる。しかしこれは \(x = \xi_{0}\) における連続性と矛盾する。
次に \(\phi(\xi_{0}) = \eta - k \lt \eta\) と仮定する。すると \(\xi_{0}\) より大きい任意の \(\xi'\) は \(R\) に含まれるので、\(\phi(\xi') \geq \eta\) が成り立つか、\(\xi_{0}\) と \(\xi'\) の間にある \(\xi''\) で \(\phi(\xi'') \geq \eta\) が成り立つ。いずれの場合でも \(\xi_{0}\) に好きなだけ近い \(x\) であって \(\phi(x)\) から \(k\) 以上離れているものを見つけられるが、これは \(\phi(x)\) が \(x = \xi_{0}\) で連続という仮定と矛盾する。
よって \(\phi(\xi_{0}) = \eta\) が分かり、定理の証明が完了する。ここで証明すべき命題以上のことを示している点に注目してほしい。つまり \(\xi_{0}\) が \(\phi(x) = \eta\) となる最小の \(x\) であることが示されている。関数がある値となる \(x\) に最小値が存在するかどうかは一般の関数では明らかでないし、実は正しくない。しかし連続関数であればこれが成り立つ。
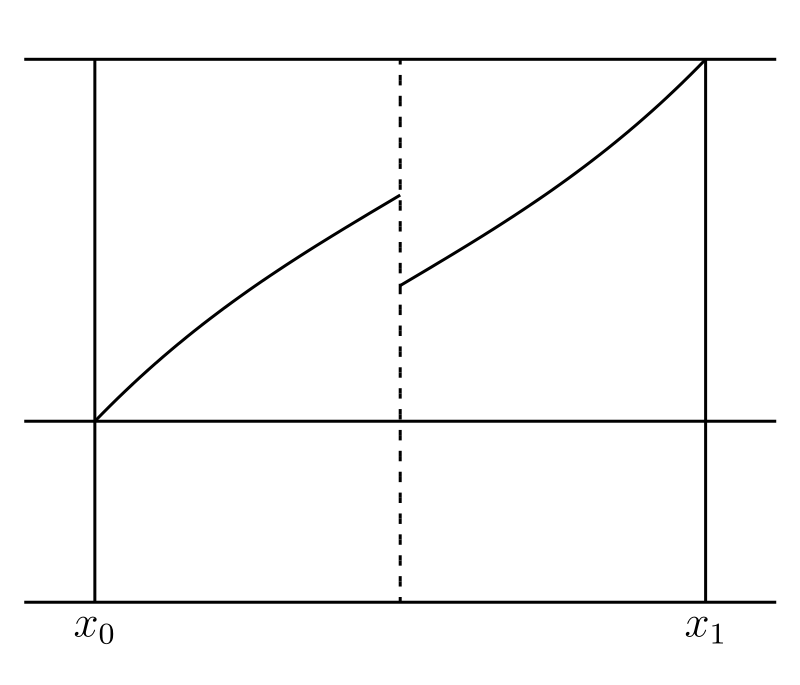
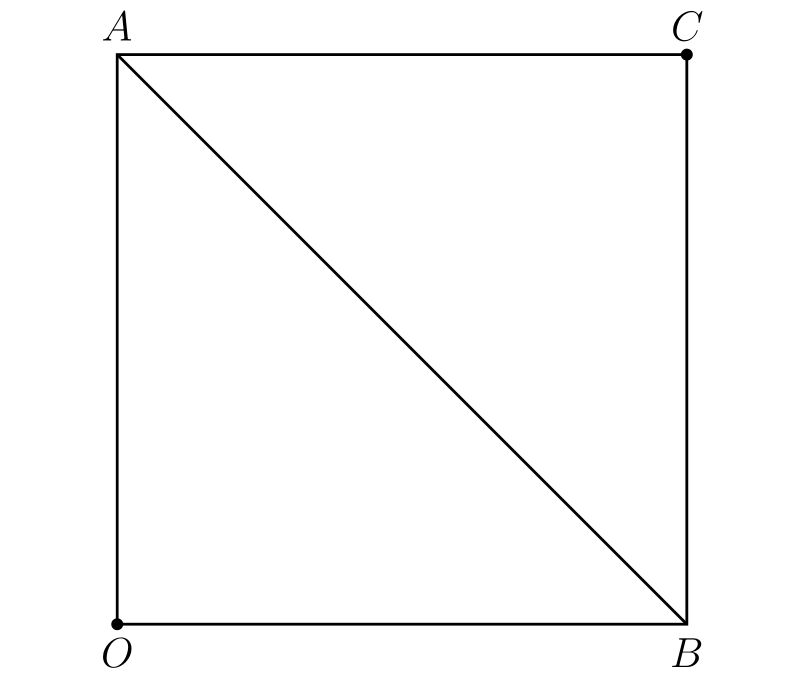
この定理の逆が正しくないことは容易に分かる。図 31 のグラフで表される関数 \(\phi(x)\) は \(\phi(x_{0})\) と \(\phi(x_{1})\) の間の全ての値を取るが、それでも \(\phi(x)\) は不連続である。さらに言えば、関数が全ての値をちょうど一度だけ取ると仮定してもなお \(\phi(x)\) は連続とならない。例えば \(\phi(x)\) を \(x = 0\) から \(x = 1\) で定義された関数として、\(x = 0\) で \(\phi(x) = 0\)、\(0 \lt x \lt 1\) で \(\phi(x) = 1 - x\)、\(x = 1\) で \(\phi(x) = 1\) とする。この関数のグラフは 図 32 のようになる。点 \(O,\ C\) はグラフに含まれるが、\(A,\ B\) は含まれない。明らかに \(x\) が \(0\) から \(1\) に移動するとき \(\phi(x)\) が \(\phi(0) = 0\) から \(\phi(1) = 1\) の全ての値をちょうど一度ずつ取るが、\(\phi(x)\) は \(x = 0\) と \(x = 1\) で不連続となる。
しかし実際のところ、初等数学に登場する曲線は \(\bm{y}\) が同じ方向に変化する曲線の有限個の集まりであることが多い。もし \(x\) が \(x_{0}\) から \(x_{1}\) まで動くとき \(y = \phi(x)\) が同じ方向に変化する、つまり \(\phi(x)\) が単調増加または単調減少なら、二つの連続の概念は一致する。つまり \(\phi(x)\) が \(\phi(x_{0})\) から \(\phi(x_{1})\) までの全ての値を取るなら、\(\phi(x)\) は §98 の意味で連続となる。証明を次に示す。\(\xi\) を \(x_{0} \lt \xi \lt x_{1} \) となるように取る。\(x\) が左から \(\xi\) に向かうとき \(\phi(x)\) は極限 \(\phi(\xi - 0)\) に向かう (§95)。同様に \(x\) が右から \(\xi\) に向かうとき \(\phi(x)\) は極限 \(\phi(\xi + 0)\) に向かう。関数が \(x = \xi\) で連続となる必要十分条件は \[ \phi(\xi - 0) = \phi(\xi) = \phi(\xi + 0) \] だった。もし一つ目の等式が成り立たないなら、\(\phi(x)\) は単調増加より \(\phi(\xi - 0)\) から \(\phi(\xi)\) の間の値を取らないことが分かるが、これは仮定と矛盾する。よって \(\phi(x)\) は連続だと分かる。以上の議論と前節の結果を合わせると、私たちが常識的に思い描く "連続" という概念がおおむね正確なこと、そして数学の言葉を使えばそれを正確に表せることが分かる。