§2 数直線上の点を使った有理数の表現

数学的な解析の様々な場面において、幾何学的な図を使うと議論が分かりやすくなる。

ただし幾何学的な図を使ったとしても、解析にその図が必要なわけでは決してない。図は図に過ぎず、説明を分かりやすくするためだけに使われる。そのため、初等幾何学の概念を使った論理的な議論は必ずしも必要とならない。図が真実からどれほど離れていたとしても、図の意味することをお互いに理解できれば、それで問題ない。

直線 (straight line)・直線の線分 (segment)・線分の長さ (length) の意味を読者は知っているものとする。両方向に無限に伸びる直線 \(\Lambda\) と適当な長さを持つ線分 \(A_{0}A_{1}\) を取る。\(A_{0}\) を原点 (origin) あるいは点 \(0\)、\(A_{1}\) を点 \(1\) と呼び、この二つの点がそれぞれ数 \(0\) と \(1\) を表すとみなす。

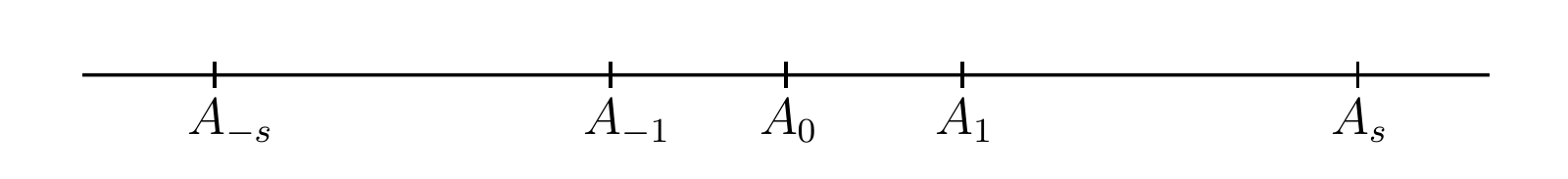
正の有理数 \(r = p/q\) を表す点を得るには、点 \(A_{r}\) を次の等式が満たされるように取る: \[ \frac{A_{0}A_{r}}{A_{0}A_{1}} = r \] ここで \(A_{0}A_{r}\) は \(A_{0}A_{1}\) と同じ方向に伸びるとする。直線を紙上に水平に書くときは、この方向を 図 1 のように左から右とする。負の有理数 \(r = -s\) を表す点を得るには、長さを符号を持つ量とみなし、ある方向 (\(A_{0}A_{1}\) の方向) に伸びるときには正を、それと反対に伸びるときには負を表すとするのが自然であり、このとき \(AB = -BA\) となる。そして \(r\) を表す点 \(A_{-s}\) は次の等式が成り立つように取る: \[ A_{0}A_{-s} = -A_{-s}A_{0} = -A_{0}A_{s} \]

ここから正と負の全ての有理数 \(r\) に対応する直線上の点 \(A_{r}\) が得られ、次式が成り立つ: \[ A_{0}A_{r} = r · A_{0}A_{1} \] \(A_{0}A_{1}\) が単位長を持つとして \(A_{0}A_{1} = 1\) とするのが自然であり、このとき \[ A_{0}A_{r} = r \] が成り立つ。有理数に対応するこの点 \(A_{r}\) を直線上の有理点 (rational points) と呼ぶ。