§59 極限の定義 (その 2)
極限の定義は次のように図示できる。\(\phi(n)\) のグラフは \(n = 1,\ 2,\ 3,\ \ldots\) に対応する無数の点からなる。
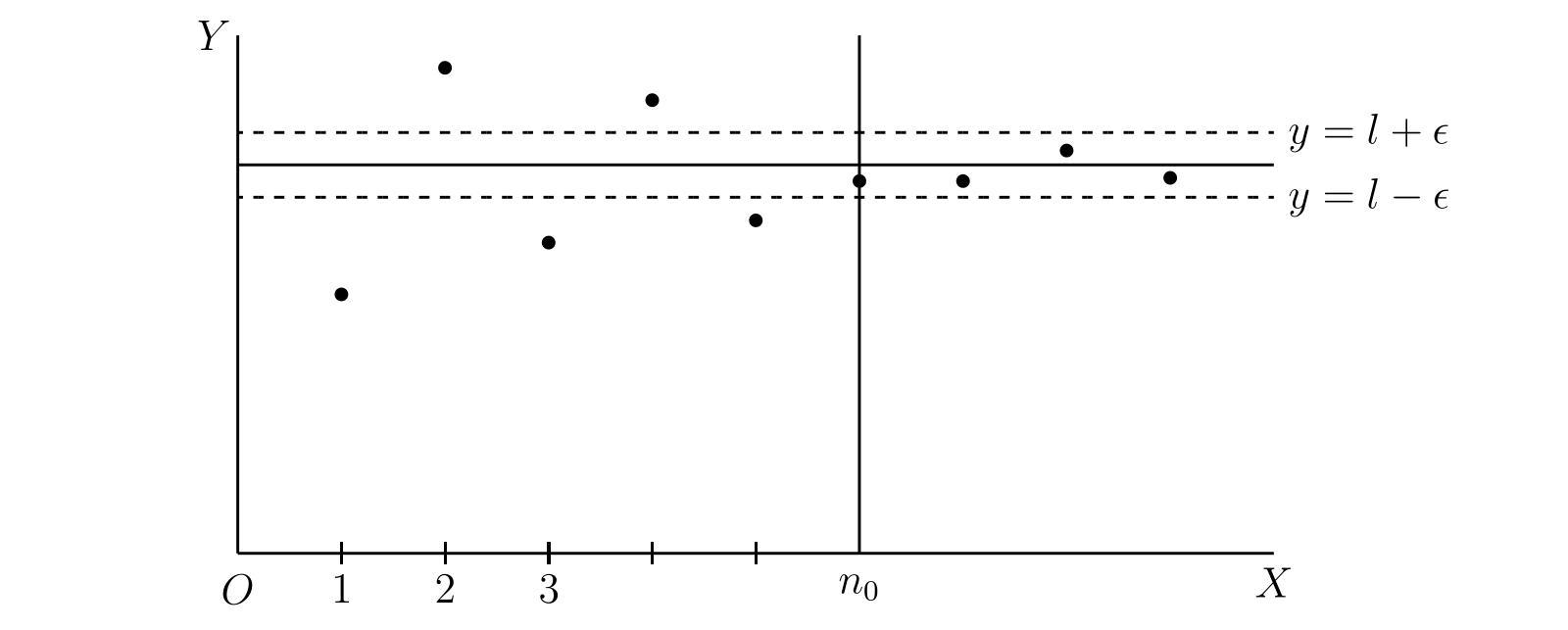
図 27
直線 \(y = l\) を描き、そこから \(\varepsilon\) だけ離れた平行な二直線 \(y = l - \varepsilon,\ y = l + \varepsilon\) を描く。すると \[ \lim_{n \to \infty} \phi(n) = l \] となるのは、二つの直線の隙間がどれだけ小さくとも、直線 \(x = n_{0}\) を引いてこの直線よりも右にある全ての点が二つの直線の間にあるようにできるときとなる。この幾何学的な定義の捉え方は、正の整数ではなく全ての実数に対して定義される関数を考えるときに特に重要となる。