§235 対数級数 (その 2)
ここまでの議論から次の等式が分かる: \[ \begin{aligned} \log(1 + z) & = \log\{(1 + r \cos\theta) + ir\sin\theta\} \\ & = \dfrac{1}{2} \log(1 + 2r\cos\theta + r^{2}) + i\arctan \left(\frac{r\sin\theta}{1 + r\cos\theta}\right) \end{aligned} \]
この等式におけるタンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取らなければならない。\(1 + z\) が \(-1\) から \(z\) への直線で表されるので、円 \(|z| = 1\) の内部にある \(z\) に対しては \(\arg(1 + z)\) の主値は常にこの範囲にある。
\(z^{m} = r^{m}(\cos m\theta + i\sin m\theta)\) だから、§234 の等式 \(\text{(5)}\) と実部と虚部をそれぞれ比較して \[ \begin{aligned} \dfrac{1}{2} \log(1 + 2r\cos\theta + r^{2}) & = r\cos\theta - \dfrac{1}{2}r^{2} \cos 2\theta + \dfrac{1}{3}r^{3} \cos 3\theta - \cdots, \\ \arctan \left(\frac{r\sin\theta}{1 + r\cos\theta}\right) & = r\sin\theta - \dfrac{1}{2}r^{2} \sin 2\theta + \dfrac{1}{3}r^{3} \sin 3\theta - \cdots \end{aligned} \] を得る。この二つの等式は \(0 \leq r \leq 1\) で全ての \(\theta\) に対して成り立つが、唯一の例外として \(r = 1\) のときは \(\theta\) が \(\pi\) の倍数であってはならない。
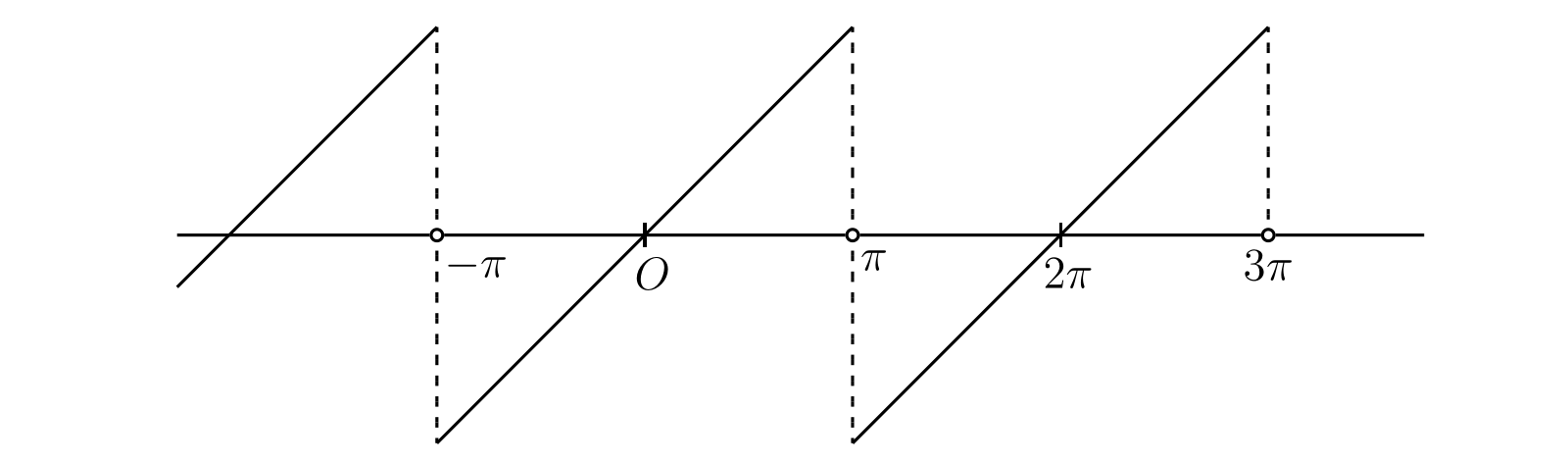
特に興味深いのが \(r = 1\) の場合で、このとき \(-\pi \lt \theta \lt \pi\) で \[ \begin{aligned} \log(1 + z) & = \log(1 + \operatorname{Cis}\theta) \\ & = \dfrac{1}{2} \log(2 + 2\cos\theta) + i\arctan\left(\frac{\sin\theta}{1 + \cos\theta}\right) \\ & = \dfrac{1}{2} \log(4\cos^{2} \dfrac{1}{2}\theta) + \dfrac{1}{2}i\theta \end{aligned} \] が成り立つ。つまり \[ \begin{alignedat}{4} \cos\theta & - \dfrac{1}{2} \cos 2\theta & & + \dfrac{1}{3} \cos 3\theta & & - \cdots & & = \dfrac{1}{2} \log(4\cos^{2} \dfrac{1}{2}\theta), \\ \sin\theta & - \dfrac{1}{2} \sin 2\theta & & + \dfrac{1}{3} \sin 3\theta & & - \cdots & & = \dfrac{1}{2} \theta \end{alignedat} \] である。他の \(\theta\) に対する級数の和を計算するには、二つの級数が \(\theta\) に関する周期 \(2\pi\) の周期関数である事実を使う。するとコサインの級数の和は \(\theta\) が \(\pi\) の奇数倍となる (級数が発散する) 場合を除いた全ての \(\theta\) で \(\frac{1}{2} \log(4\cos^{2} \frac{1}{2}\theta)\) となり、サインの級数の和は \((2k - 1)\pi \lt \theta \lt (2k + 1)\pi\) で \(\frac{1}{2} (\theta - 2k\pi)\) そして \(\theta\) が \(\pi\) の奇数倍なら \(0\) となることが分かる。このサイン級数が表す関数のグラフを 図 58 に示す。この関数は \(\theta = (2k + 1)\pi\) で不連続となる。
\(\text{(5)}\) の \(z\) を \(iz\) および \(-iz\) に書き換えて引くと \[ \frac{1}{2i} \log\left(\frac{1 + iz}{1 - iz}\right) = z - \dfrac{1}{3}z^{3} + \dfrac{1}{5}z^{5} - \cdots \] を得る。§231 の結果から、絶対値が \(1\) より小さい実数 \(z\) に対する \[ \arctan z = z - \dfrac{1}{3}z^{3} + \dfrac{1}{5}z^{5} - \cdots \] が導かれる。これは §214 で異なる方法を使って示した公式である。
-
\(a \gt b\) が成り立つ任意の三角形で \[ \log c = \log a - \frac{b}{a} \cos C - \frac{b^{2}}{2a^{2}} \cos 2C - \cdots \] だと示せ。[等式 \(\log c = \frac{1}{2} \log(a^{2} + b^{2} - 2ab\cos C )\) を使う]
-
\(-1 \lt r \lt 1\) かつ \(-\frac{1}{2}\pi \lt \theta \lt \frac{1}{2}\pi\) なら \[ r\sin 2\theta - \dfrac{1}{2}r^{2} \sin 4\theta + \dfrac{1}{3}r^{3} \sin 6\theta - \cdots = \theta - \arctan \left\{\left(\frac{1 - r}{1 + r}\right) \tan\theta\right\} \] だと示せ。タンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取るとする。任意の \(\theta\) に対する級数の和を計算せよ。
-
\(\log(1 + iz)\) と \(\log(1 - iz)\) を \(z\) のべき級数へ展開することで、\(-1 \lt r \lt 1\) に対する \[ \begin{gathered} \begin{alignedat}{4} r\sin\theta & + \dfrac{1}{2}r^{2} \cos 2\theta & & - \dfrac{1}{3}r^{3} \sin 3\theta & & - \dfrac{1}{4}r^{4} \cos 4\theta + \cdots & & = \dfrac{1}{2} \log(1 + 2r \sin\theta + r^{2}),\\ r\cos\theta & + \dfrac{1}{2}r^{2} \sin 2\theta & & - \dfrac{1}{3}r^{3} \cos 3\theta & & - \dfrac{1}{4}r^{4} \sin 4\theta + \cdots & & = \arctan \left(\frac{r\cos\theta}{1 - r\sin\theta}\right), \end{alignedat} \\ \begin{alignedat}{2} r\sin\theta & - \dfrac{1}{3}r^{3} \sin 3\theta + \cdots & & = \dfrac{1}{4} \log\left(\frac{1 + 2r \sin\theta + r^{2}} {1 - 2r \sin\theta + r^{2}}\right),\\ r\cos\theta & - \dfrac{1}{3}r^{3} \cos 3\theta + \cdots & & = \dfrac{1}{2} \arctan \left(\frac{2r\cos\theta}{1 - r^{2}}\right) \end{alignedat} \end{gathered} \] を示せ。タンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取るとする。
-
次を示せ: \[ \begin{alignedat}{3} \cos\theta \cos\theta & - \dfrac{1}{2} \cos 2\theta \cos^{2}\theta & & + \dfrac{1}{3} \cos 3\theta \cos^{3} \theta - \cdots & & = \dfrac{1}{2} \log(1 + 3\cos^{2} \theta),\\ \sin\theta \sin\theta & - \dfrac{1}{2} \sin 2\theta \sin^{2}\theta & & + \dfrac{1}{3} \sin 3\theta \sin^{3} \theta - \cdots & & = \operatorname{arccot} (1 + \cot\theta + \cot^{2}\theta) \end{alignedat} \] タンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取るとする。次の級数の和に対する同様の表現を求めよ: \[ \cos\theta \sin\theta - \dfrac{1}{2} \cos 2\theta \sin^{2}\theta + \cdots,\quad \sin\theta \cos\theta - \dfrac{1}{2} \sin 2\theta \cos^{2}\theta + \cdots \]