§44 アルガン図

図 24 で \(P\) を点 \((x, y)\) とし、\(r\) を \(OP\) の長さ、\(\theta\) を \(\angle XOP\) とすると次が成り立つ: \[ x = r\cos\theta,\quad y = r\sin\theta,\quad r = \sqrt{x^{2} + y^{2}},\quad \cos\theta : \sin\theta : 1 = x : y : r \]

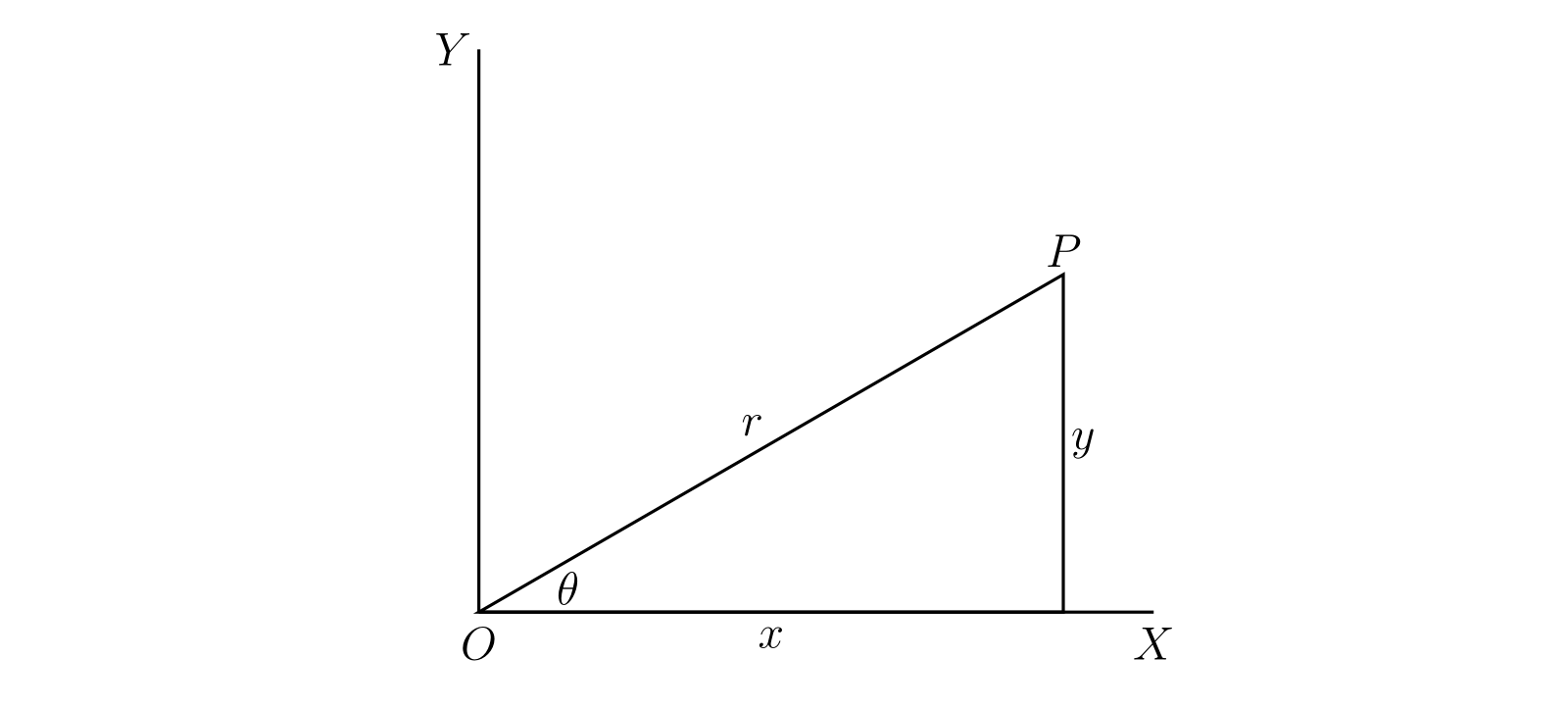
§43 と同様に \(x + yi\) を \(z\) と表記し、\(z\) を複素変数 (complex variable) と呼ぶ。そして \(P\) は点 \(\bm{z}\)、あるいは \(z\) に対応する点と呼び、\(z\) は \(P\) の引数 (argument)、\(x\) は \(z\) の実部 (real part)、\(y\) は \(z\) の虚部 (imaginary part)、\(r\) は \(z\) の大きさ (modulus)、\(\theta\) は \(z\) の 偏角 (argument)¹ と呼ぶ。そして次のように表記する: \[ x = \operatorname{Re}(z),\quad y = \operatorname{Im}(z),\quad r = |z|,\quad \theta = \arg z \]

\(y = 0\) のとき \(z\) を実数と呼び、\(x = 0\) のとき \(z\) を純虚数 (pure imaginary number)と呼ぶ。虚部の符号だけが異なる二つの複素数 \(x + yi\) と \(x - yi\) は共役 (conjugate) であると言う。共役な複素数の和 \(2x\) と積 \(x^{2} + y^{2}\) は両方とも実数であり、二つの大きさ \(\sqrt{x^{2} + y^{2}}\) は等しく、大きさは積の二乗に等しい。例えば実数係数二次方程式の二つの根が実数でない場合、それらは共役となる。

\(\theta\) すなわち \(\arg z\) は \(x\) と \(y\) の多値関数であり、\(2\pi\) だけ離れた値を無限に取ることに注意する必要がある²。\(OX\) 上にある直線を原点を中心にこれらの角度だけ回転させると、その直線は \(OP\) に向くようになる。この中で \(-\pi\) から \(\pi\) にある角度を、\(z\) の偏角の主値 (principal value) と呼ぶ。どの値を主値とするかは事前に決めておかなくてはならない。これからは、明示的に示さない限り、「\(z\) の偏角」で \(z\) の偏角の主値を表す。

図 24 をアルガン図 (Argand's diagram) と呼ぶ。

1. 訳注: 原文では \(\theta\) を「振幅 (amplitude)」と呼んでいるが、これは標準的ではないので変更した。以降の \(\arg\) も原文では全て \(\text{am}\) となっている。^[return]

2. \(|z|\) は \(P\) を極座標で表したときの \(r\) に等しく、極座標のもう一方 \(\theta\) は \(\arg z\) に等しい。ただし \(\theta\) がここで定義される主値であるとは限らない。§22 で定義した極座標は \(0\) から \(2\pi\) の角度を使うが、主値は \(-\pi\) から \(\pi\) なためである。^[return]