§145 平面曲面の面積

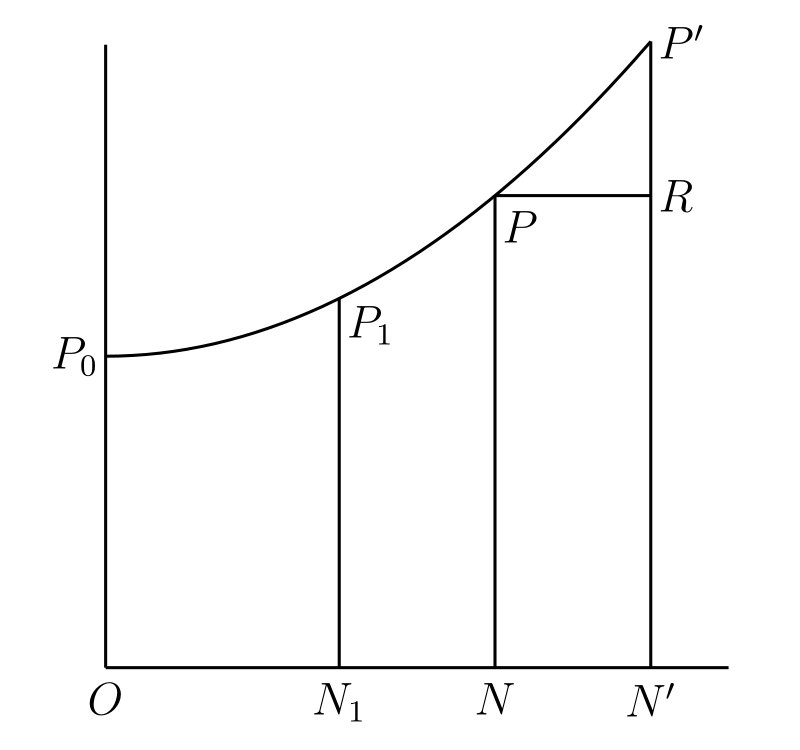
ここまで説明してきた積分の最も重要な応用は、平面曲線の面積の計算である。連続曲線 \(y = \phi(x)\) のグラフ \(P_{0}PP'\) (図 44) が \(x\) 軸の上方にあると仮定し、\(P\) が点 \((x, y)\) で \(P'\) が点 \((x + h, y + k)\) だとする。\(h\) は正でも負でもよい (図では正としている)。

読者は「面積」の意味を当然知っており、特に「\(ONPP_{0}\) の面積」と言ったときに何を意味するかを知っていると思う。ここでは面積という概念が数学的な定義なしに定められているものとする。実は "面積" は最も詳細な数学的解析を必要とする概念であり、これまでにたくさんの解析がなされてきた。以降の章ではこの問題に立ち返り、\(ONPP_{0}\) などの領域の「面積」が正確に何を意味するのかを説明する。ただ今の段階では、そういった領域にとある正の実数 \((ONPP_{0})\) が対応付いているのだと単純に仮定して話を進める。この実数は面積と呼ばれ、次に示すような常識的に明らかな性質を持つ: \[ (PRP') + (NN'RP) = (NN'P'P),\quad (N_{1}NPP_{1}) \lt (ONPP_{0}) \]

こういった仮定の下で \(ONPP_{0}\) が \(x\) の関数となるのは明らかである。これを \(\Phi(x)\) と表記する。次の関係が成り立つので、\(\Phi(x)\) が 連続関数だとも分かる: \[ \begin{aligned} \Phi(x + h) - \Phi(x) & = (NN'P'P)\\ & = (NN'RP) + (PRP') = h\phi(x) + (PRP') \end{aligned} \]

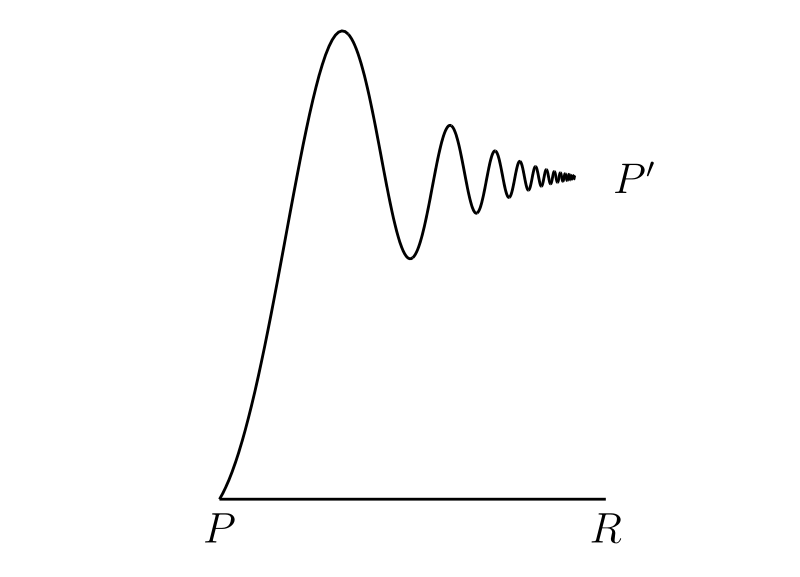
今考えている図では \(PRP'\) の面積は \(hk\) より小さいが、これは常に成り立つわけではない。弧 \(PP'\) が \(P\) から \(P'\) に向かうときに単調に増加あるいは減少するとは限らないためである (例えば 図 44a)。しかし \(\lambda(h)\) を \(PR\) から \(PP'\) 上の任意の点への距離の最大値とすれば、\(PRP'\) の面積は \(|h|\lambda(h)\) より小さくなる。また \(\phi(x)\) は連続関数だから、\(h \to 0\) のとき \(\lambda(h) \to 0\) が成り立つ。よって \[ \Phi(x + h) - \Phi(x) = h\{\phi(x) + \mu(h)\} \] となる。ここで \(|\mu(h)| \lt \lambda(h)\) かつ \(h \to 0\) のとき \(\lambda(h) \to 0\) である。この式からも \(\Phi(x)\) が連続だと直ちに分かる。さらに \[ \Phi'(x) = \lim_{h \to 0} \frac{\Phi(x + h) - \Phi(x)}{h} = \lim_{h \to 0} \{\phi(x) + \mu(h)\} = \phi(x) \] だから、曲線の \(\bm{y}\) 座標は面積の導関数で、曲線の \(\bm{y}\) 座標の積分は面積となる。

以上の議論から \(ONPP_{0}\) の面積を計算する方法が定式化できる: まず \(\phi(x)\) の積分 \(\Phi(x)\) を計算する。\(\Phi(x)\) には任意定数が含まれるから、\(\Phi(0) = 0\) となるようにそれを選ぶ。すると求める面積は \(\Phi(x)\) となる。