§38 変位の積の正しい定義
採用すべき正しい定義は次の通りである。\(\triangle OAB\) と \(\triangle OCD\) を対応する角度がこの順番の相似な三角形とする。このとき \[ OB/OA = OD/OC \] および \(OB · OC = OA · OD\) が成り立つ。ここから次に示す変位の乗算と除算の定義が提案される: \[ \overline{OB}/\overline{OA} = \overline{OD}/\overline{OC},\quad \overline{OB} · \overline{OC} = \overline{OA} · \overline{OD} \]
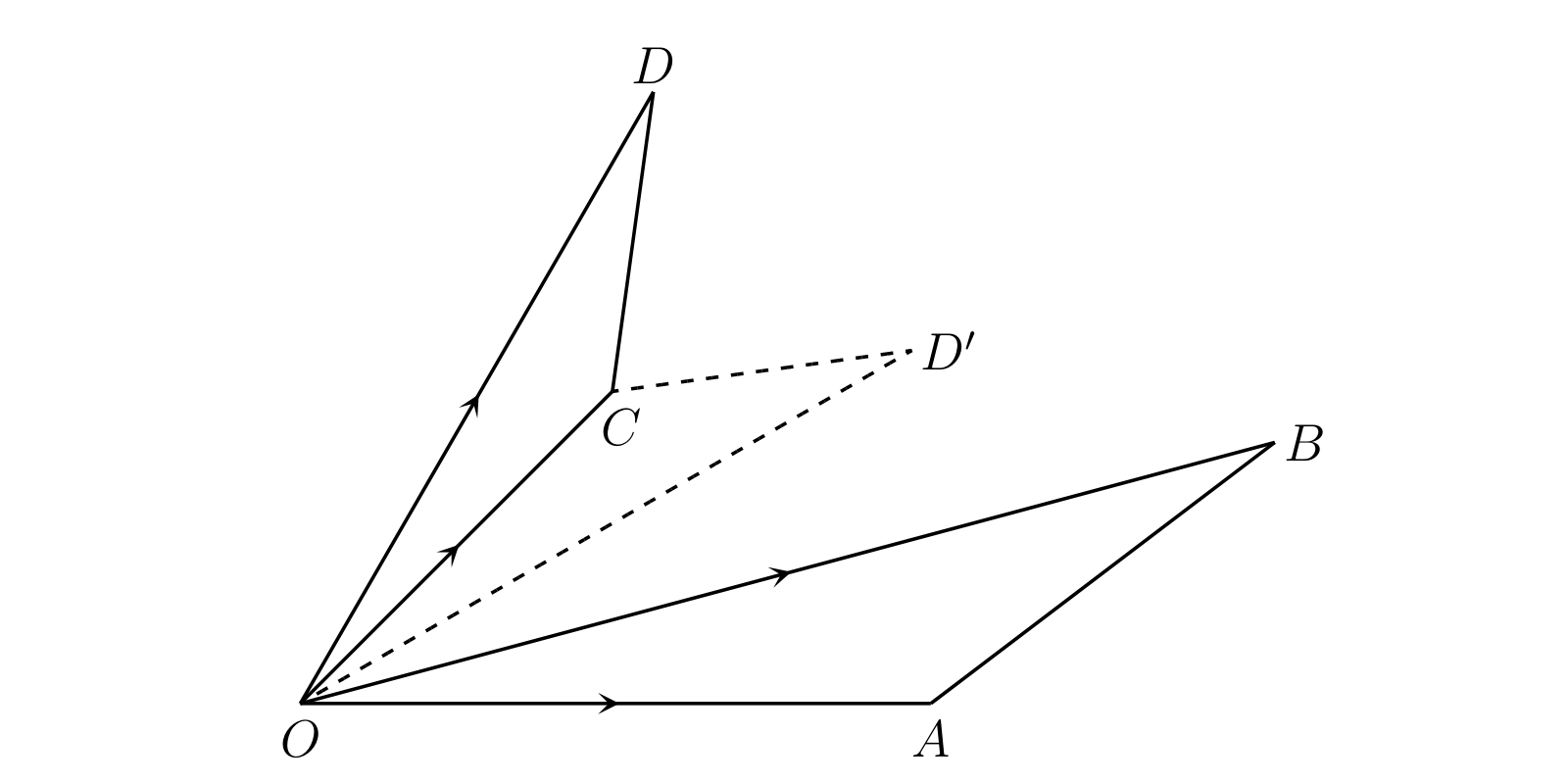
ここで \[ \overline{OB} = [x, y],\quad \overline{OC} = [x', y'],\quad \overline{OD} = [X, Y] \] として、\(A\) を点 \((1, 0)\) と仮定する。すると \(\overline{OA} = [1, 0]\) であり、 \[ \overline{OA} · \overline{OD} = [1, 0] [X, Y] = [X, Y] \] および \[ [x, y] [x', y'] = [X, Y] \] が成り立つ。つまり積 \(\overline{OB} · \overline{OC}\) を \(\overline{OD}\) と定義すれば、\(D\) は \(OC\) 上に \(\triangle OAB\) と相似な三角形を作ったときの頂点となる。ただし定義に曖昧さがあり、\(OC\) から作れる三角形が (\(\triangle OCD\) と \(\triangle OCD'\) の) 二つある点に注意が必要となる。ここでは \(\angle COD\) と \(\angle AOB\) が向きも含めて等しくなるように選ぶ。このとき二つの三角形は向きを含めて相似であると言う。
\(B\) と \(C\) の極座標がそれぞれ \((\rho, \theta)\) と \((\sigma, \phi)\) なら、 \[ x = \rho\cos\theta,\quad y = \rho\sin\theta,\quad x' = \sigma\cos\phi,\quad y' = \sigma\sin\phi \] が成り立つ。このとき \(D\) の極座標は \((\rho\sigma, \theta + \phi)\) なので、 \[ \begin{alignedat}{3} X & = \rho\sigma\cos(\theta + \phi) & & = xx' - yy',\\ Y & = \rho\sigma\sin(\theta + \phi) & & = xy' + yx' \end{alignedat} \] が分かる。よって定義は次のように表せる: \[ [x, y] [x', y'] = [xx' - yy', xy' + yx'] \qquad \text{(6)} \]
この定義は必要とされる通り (1) \(y = 0\) なら \(X = xx',\ Y = xy'\) となる。さらに (2) 右辺は \(x\) と \(x'\) および \(y\) と \(y'\) を入れ替えても変わらず \[ [x, y] [x', y'] = [x', y'] [x, y] \] であることも確認できる。また (3) 次の式も成り立つ: \[ \begin{aligned} \{[x, y] + [x', y']\} [x'', y''] & = [x + x', y + y'] [x'', y'']\\ & = [(x + x') x'' - (y + y') y'', (x + x') y'' + (y + y') x'']\\ & = [xx'' - yy'', xy'' + yx''] + [x'x'' - y'y'', x'y'' + y'x'']\\ & = [x, y] [x'', y''] + [x', y'] [x'', y''] \end{aligned} \]
同様に §37 の最後であげた等式は全て確認できる。よって定義 (6) は §37 で示した要件を全て満たす。
変位の積が交換法則、分配法則、結合法則を満たすことを、上述の幾何学的な定義から直接示せ。 [例として交換法則を示す。\(\overline{OB}\) と \(\overline{OC}\) の積は \(\overline{OD}\) で、\(\triangle COD\) は \(\triangle AOB\) と相似である (図 22)。\(\overline{OC} · \overline{OB}\) を得るには、\(OB\) 上に \(\triangle AOC\) と相似な \(\triangle BOD_{1}\) を取る。後は \(D\) と \(D_{1}\) が等しいこと、つまり \(\triangle BOD\) と \(\triangle AOC\) が相似なことを証明すればよい。これは簡単な初等幾何学の問題である]