§71 ワイエルシュトラスの定理の別証明
§69 の結果を使うと、§19 で示した重要な定理の別証明が可能になる。
\(PQ\) を二つの等しい部分に分ける。二つの部分の少なくとも一方は \(S\) の点を無限に含むので、それを \(P_{1}Q_{1}\) とする (図 28)。両方が無限の点を含むときは左側の部分を選ぶ。
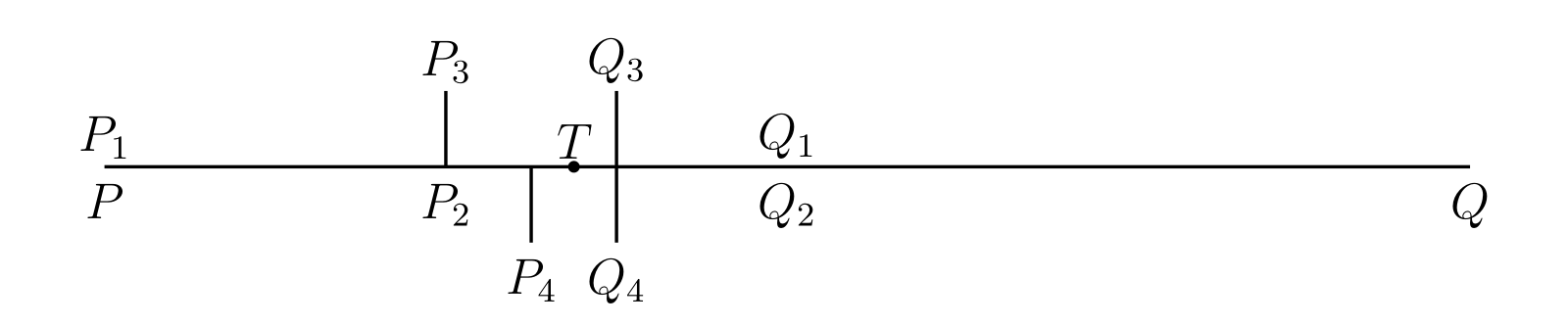
同様に \(P_{1}Q_{1}\) を二つの等しい部分に分ければ、少なくとも一方は \(S\) の点を無限に含む。無限の点を含むのが片方だけならそれを \(P_{2}Q_{2}\) とし、両方が含むときは左側の部分を \(P_{2}Q_{2}\) とする。この操作を繰り返すと区間の無限列 \[ PQ,\quad P_{1}Q_{1},\quad P_{2}Q_{2},\quad P_{3}Q_{3},\quad \ldots, \] を定義できる。各区間は一つ前の区間の半分であり、全ての区間は \(S\) の点を無限に含む。
点 \(P,\ P_{1},\ P_{2},\ \ldots\ \) は左から右へ単調に移動するので、\(P_{n}\) は極限の点 \(T\) に向かう。同様に \(Q_{n}\) も極限の点 \(T'\) に向かう。しかし明らかに、どんな \(n\) に対しても \(TT'\) は \(P_{n}Q_{n}\) よりも小さい。\(P_{n}Q_{n}\) の長さは \(PQ/2^{n}\) であり、\(0\) に向かう。そのため \(T'\) と \(T\) は一致し、\(P_{n}\) と \(Q_{n}\) はどちらも \(T\) に向かう。
このとき \(T\) は \(S\) の集積点となる: \(\xi\) を \(T\) の座標として \(\xi - \varepsilon, \xi + \varepsilon\) という形の区間を考えると、十分大きな \(n\) では \(P_{n}Q_{n}\) がこの区間に完全に含まれる1ので、\([\xi - \varepsilon, \xi + \varepsilon]\) は \(S\) の点を無限に含む。
-
具体的には \(PQ/2^{n} \lt \varepsilon\) となればよい。[return]