§158 扇形の面積と三角関数
\(\cos x\) や \(\sin x\) をはじめとした三角関数の理論が初等三角法の教科書で説明されるときには、証明されない仮定が最初におかれる場合が多い。二つの直線 \(OA\) と \(OP\) は角度 (angle) を定めるが、この「幾何学的な」定義を純粋に解析的な用語として採用することに問題はない。問題はこの次の、角度は数値として表せるという仮定にある。つまりここでは、図 47 の領域 \(PpqQ\) に対応する実数の存在と同じように、二つの直線の位置関係に対応する実数 \(x\) の存在が仮定されている。この点さえ認めれば、後は \(\cos x\) や \(\sin x\) が通常通りに定義でき、以降の理論の構築で行き詰まることもない。つまり唯一の問題は \(\bm{\cos x}\) や \(\bm{\sin x}\) における \(\bm{x}\) とはいったい何なのかにある。この問題を解決するには角度の意味を定める必要があり、私たちはこれからこれを行う。最も自然な定義は次のようになる: \(O\) を中心とした半径 \(1\) の円の弧を \(AP\) とすれば \(OA = OP = 1\) が成り立つ。そして角度の大きさを表す実数 \(x\) を 弧 \(\bm{AP}\) の長さと定める。この定義はたいていの教科書で採用されるものであり、"弧度法" の理論がここから展開される。しかし今の目的に照らして考えると致命的な欠陥がある。曲線の長さは面積と同じように詳細な数学的な解析が可能な概念であり、その解析はこれまでの節と似てはいるものの明らかにより難しい。そのため曲線の長さをここで一般的に扱うなどとてもできない。
つまり長さではなく面積を使って角度を定義しなければならない。そこで \(\angle AOP\) を 単位円上の扇形 \(\bm{AOP}\) の面積の二倍として定義する。
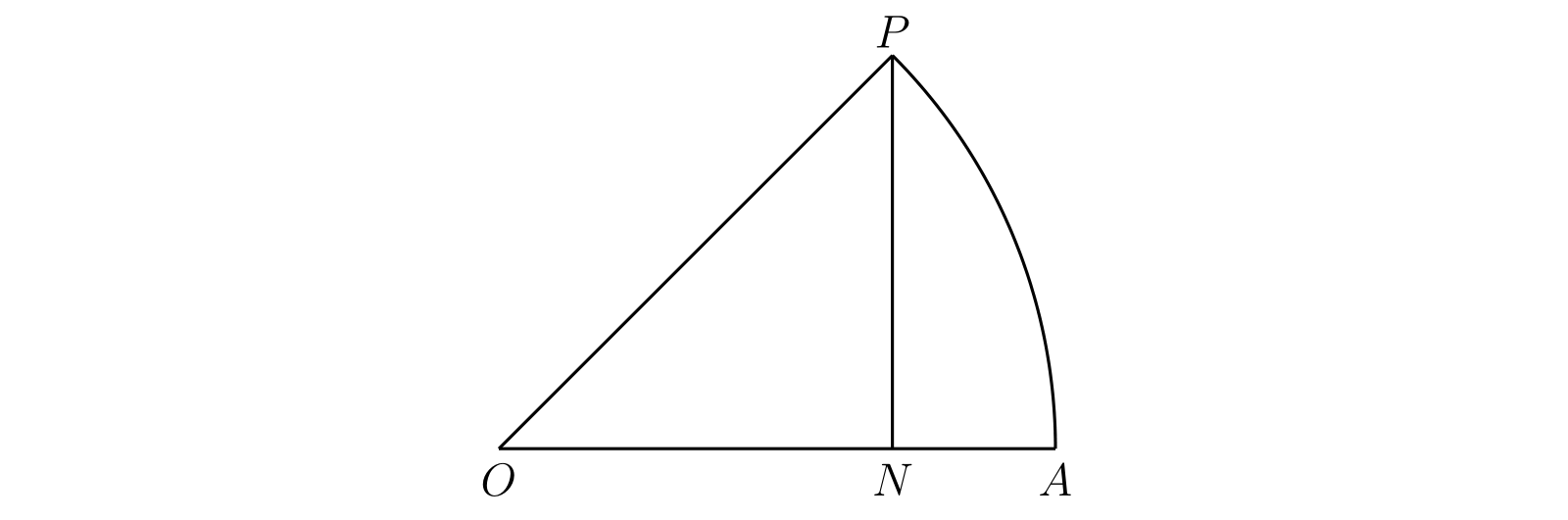
\(OA\) が \(y = 0\) で \(OP\) が \(y = mx\) である場合を考える (\(m \gt 0\))。扇形の面積は \(m\) の関数だから、これを \(\phi(m)\) と表す。\(\mu = (1 + m^{2})^{-\frac{1}{2}}\) とすれば \(P\) は点 \((\mu, m\mu)\) となり \[ \phi(m) = \dfrac{1}{2} m\mu^{2} + \int_{\mu}^{1} \sqrt{1 - x^{2}}\, dx \] が成り立つ。これを \(m\) で微分すれば \[ \phi'(m) = \frac{1}{2(1 + m^{2})},\quad \phi(m) = \dfrac{1}{2} \int_{0}^{m} \frac{dt}{1 + t^{2}} \] が分かる。よって先ほどの面積を使った角度の定義を解析的に表すには、\(\arctan m\) を等式 \[ \arctan m = \int_{0}^{m} \frac{dt}{1 + t^{2}} \] で定義すればよいと分かる。三角関数に関する理論はこの等式を始点として全て構築できる。第九章では同様の方法で対数の理論を得る。補遺 三 も参照。
不定積分を使った定積分の計算
-
次を示せ: \[ \int_{a}^{b} x^{n}\, dx = \frac{b^{n+1} - a^{n+1}}{n + 1} \] ここから特に \[ \int_{0}^{1} x^{n}\, dx = \frac{1}{n + 1} \] が分かる。
-
\(\displaystyle\int_{a}^{b} \cos mx\, dx = \frac{\sin mb - \sin ma}{m},\quad \displaystyle\int_{a}^{b} \sin mx\, dx = \frac{\cos ma - \cos mb}{m}\)
-
\(\displaystyle\int_{a}^{b}\frac{dx}{1 + x^{2}} = \arctan b - \arctan a,\quad \displaystyle\int_{0}^{1}\frac{dx}{1 + x^{2}} = \dfrac{1}{4}\pi\)
[一見すると多価関数 \(\arctan x\) が関係する積分は込み入って見えるが、等式 \[ \int_{0}^{x} \frac{dt}{1 + t^{2}} = \arctan x \] において \(\arctan x\) の表す角度が必ず \(-\frac{1}{2}\pi\) と \(\frac{1}{2}\pi\) の間にある事実が分かれば難しくない。この事実は \(x = 0\) で積分が \(0\) であり、\(x\) と共に単調増加することから分かる。つまり \(\arctan x\) も単調増加で、\(x \to \infty\) のとき \(\frac{1}{2}\pi\) に向かう。同様に \(x \to -\infty\) なら \(\arctan x \to -\frac{1}{2}\pi\) だとも示せる。同様に \(-1 \lt x \lt 1\) に対する等式 \[ \int_{0}^{x} \frac{dt}{\sqrt{1 - t^{2}}} = \arcsin x \] からは、角度 \(\arcsin x\) が \(-\frac{1}{2}\pi\) と \(\frac{1}{2}\pi\) の間にあることが分かる。よってもし \(a\) と \(b\) の絶対値が \(1\) 未満なら \[ \int_{a}^{b} \frac{dx}{\sqrt{1 - x^{2}}} = \arcsin b - \arcsin a \] が成り立つ]
-
\(\displaystyle\int_{0}^{1} \frac{dx}{1 - x + x^{2}} = \frac{2\pi}{3\sqrt3},\quad\displaystyle\int_{0}^{1} \frac{dx}{1 + x + x^{2}} = \frac{\pi}{3\sqrt3}\)
-
\(-\pi \lt \alpha \lt \pi\) なら \(\displaystyle\int_{0}^{1} \frac{dx}{1 + 2x\cos\alpha + x^{2}} = \frac{\alpha}{2\sin\alpha}\) が成り立つ。ただし \(\alpha = 0\) では \(\dfrac{1}{2}\) で、これは \(\alpha \to 0\) における \(\dfrac{1}{2}\alpha\cosec\alpha\) の極限に等しい。
-
\(\displaystyle\int_{0}^{1} \sqrt{1 - x^{2}}\, dx = \dfrac{1}{4}\pi,\quad \displaystyle\int_{0}^{a} \sqrt{a^{2} - x^{2}}\, dx = \dfrac{1}{4}\pi a^{2}\quad \) \((a \gt 0)\)
-
\(a \gt |b|\) なら \(\displaystyle\int_{0}^{\pi} \frac{dx}{a + b\cos x} = \frac{\pi}{\sqrt{a^{2} - b^{2}}}\) が成り立つ。 [不定積分の形については 例 53.3, 4 を参照。\(|a| \lt |b|\) だと \(0\) と \(\pi\) の間で被積分関数が無限大になる。\(a\) が負で \(-a \gt |b|\) のときの積分の値はどうなるか?]
-
\(a\) と \(b\) が正なら \(\displaystyle\int_{0}^{\frac{1}{2}\pi} \frac{dx}{a^{2}\cos^{2}x + b^{2}\sin^{2}x} = \frac{\pi}{2ab}\) が成り立つ。\(a\) と \(b\) が異なる符号を持つとき、あるいは両方負のときの積分の値は何か?
-
フーリエ積分: \(m\) と \(n\) を正の整数としたとき、 \[ \int_{0}^{2\pi} \cos mx \sin nx\, dx \] が常に \(0\) に等しいこと、および \[ \int_{0}^{2\pi} \cos mx \cos nx\, dx,\quad \int_{0}^{2\pi} \sin mx \sin nx\, dx \] が \(m = n\) なら \(\pi\) でそれ以外のとき \(0\) となることを示せ。
-
\(\displaystyle\int_{0}^{\pi} \cos mx \cos nx\, dx\) と \(\displaystyle\int_{0}^{\pi} \sin mx \sin nx\, dx\) が \(m = n\) なら \(\frac{1}{2}\pi\) で、そうでないなら \(0\) だと示せ。さらに \(n - m\) が奇数か偶数かに応じて \[ \int_{0}^{\pi} \cos mx \sin nx\, dx = \frac{2n}{n^{2} - m^{2}},\quad \int_{0}^{\pi} \cos mx \sin nx\, dx = 0 \] だと示せ。