§125 平均値の定理 (その 1)
続いて一般的な定理をもう一つ証明する。これはとてつもなく重要な定理であり、平均値の定理 (Mean Value Theorem, Theorem of the Mean) と呼ばれることが多い。
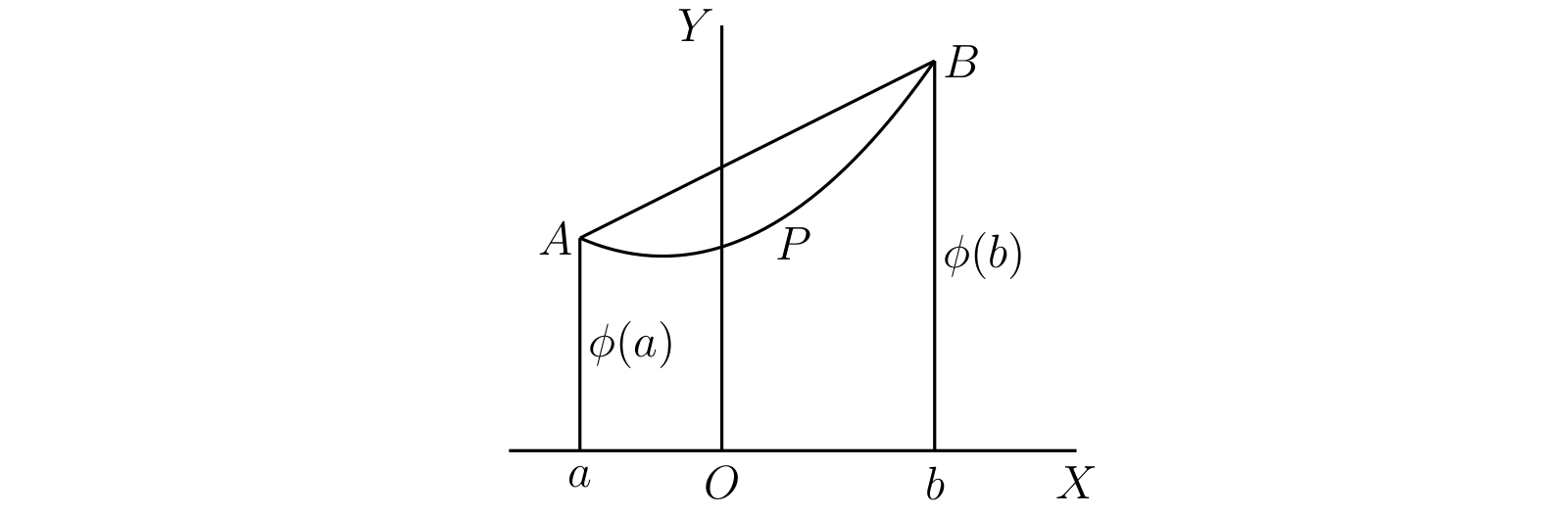
区間 \([a, b]\) 内の全ての \(x\) に対して \(\phi(x)\) が微分係数を持つとする。このとき \(a\) と \(b\) の間にある \(\xi\) であって \[ \phi(b) - \phi(a) = (b - a)\phi'(\xi) \] を満たすものが存在する。
おそらく微分積分学において最も重要なこの定理の厳密な証明を示す前に、その簡単な幾何学的意味を確認しておく。この定理は単に、図 43 のように曲線 \(APB\) 上の全ての点で接線を引けるとき、接線が \(AB\) と平行になる (\(P\) のような) 点が存在することを意味する。\(\phi'(\xi)\) は \(P\) で引いた接線と \(OX\) がなす角度のタンジェントであり、\(\{\phi(b) - \phi(a)\}/(b - a)\) は \(AB\) と \(OX\) がなす角度のタンジェントを表すためである。
解析的な議論を使った厳密な証明も簡単に行える。関数 \[ \phi(b) - \phi(x) - \frac{b - x}{b - a}\{\phi(b) - \phi(a)\} \] は \(x = a\) と \(x = b\) で \(0\) となる。§121 の定理 B から、この関数の導関数が \(0\) になる \(\xi\) が存在すると分かる。一方で導関数は \[ \frac{\phi(b) - \phi(a)}{b - a} - \phi'(x) \] なので、定理が証明される。この証明では \(\phi'(x)\) の連続性が仮定されていない点に注意してほしい。
平均値の定理を次の形で表すと便利な場合が多い: \[ \phi(b) = \phi(a) + (b - a) \phi'\{a + \theta(b - a)\} \] ここで \(\theta\) は \(0\) と \(1\) の間の実数を表す。もちろん \(a + \theta(b - a)\) というのは「\(a\) と \(b\) の間のとある数 \(\xi\)」を言い換えたに過ぎない。\(b = a + h\) とすれば \[ \phi(a + h) = \phi(a) + h\phi'(a + \theta h) \] を得る。平均値の定理はこの形で表されることが一番多い。
-
式 \[ \phi(b) - \phi(x) - \frac{b - x}{b - a}\{\phi(b) - \phi(a)\} \] が曲線上の点と弦上の点の \(y\) 座標の差を表すことを示せ。
-
\(\phi(x) = x^{2}\) と \(\phi(x) = x^{3}\) で中間値の定理が成り立つことを確認せよ。
[\(\phi(x) = x^{3}\) では、\(a \lt \xi \lt b\) で \((b^{3} - a^{3})/(b - a) = 3\xi^{2}\) だと示す必要がある。つまり \(\frac{1}{3}(b^{2} + ab + a^{2}) = \xi^{2}\) なら \(\xi\) が \(a\) と \(b\) の間にあることを証明する]
-
§124 の最後で説明した定理を平均値の定理を使って示せ。
[\(\phi'(0) = c\) だから、小さい正の \(x\) であって \(\{\phi(x) - \phi(0)\}/x\) が \(c\) にほぼ等しいものを見つけられる。よって平均値の定理から、小さい正の \(\xi\) であって \(\phi'(\xi)\) が \(c\) にほぼ等しいものが存在する。これは \(a = c\) でない限り \(\lim\limits_{x \to +0} \phi'(x) = a\) と矛盾する。同様に \(b = c\) も分かる]
-
平均値の定理を使って §113 の結果 6 を示せ。登場する導関数は全て連続だと仮定してよい。
[\(F\{f(x)\}\) の導関数は定義より \[ \lim \frac{F\{f(x + h)\} - F\{f(x)\}}{h} \] である。中間値の定理から、\(x\) と \(x + h\) の間にある \(\xi\) で \(f(x + h) = f(x) + hf'(\xi)\) が成り立つ。さらに \(f(x)\) と \(f(x) + hf'(\xi)\) の間にある \(\xi_{1}\) で \[ F\{f(x) + hf'(\xi)\} = F\{f(x)\} + hf'(\xi)\, F'(\xi_{1}) \] が成り立つ。\(h \to 0\) のとき \(\xi \to x\) かつ \(\xi_{1} \to f(x)\) だから、\(F\{f(x)\}\) の導関数は \[ \lim f'(\xi)\, F'(\xi_{1}) = f'(x)\, F'\{f(x)\} \] となる]