第二章 実数関数
§20 関数という考え方
連続実変数 \(x\) と \(y\) が \(A_{0}P = x\) および \(B_{0}Q = y\) として幾何学的に表されるとする。\(A_{0},\ B_{0}\) は固定されており、それぞれ直線 \(\Lambda,\ \Mu\) 上にある。ここで \(P\) と \(Q\) が好き勝手に動けるわけではなく、二つの点の間に何らかの関係性があって、それが \(x\) と \(y\) の間の関係として表せるとする。つまり \(P\) と \(x\) が分かっていれば \(Q\) と \(y\) も分かる関係、例えば \(y = x\) や \(y = 2x\)、あるいは \(y = \frac{1}{2}x\) や \(y = x^{2} + 1\) があるとする。このとき \(x\) の値が \(y\) の値を決定する。\(x\) と \(y\) の間の関係は \(x\) を使った \(y\) の明示的な式でなくてもよく、与えられた \(P\) から \(Q\) を得るための幾何学的な作図手順でも構わない。
このような状況で \(y\) は \(x\) の関数 (function) であると言う。ある変数の値が別の変数の値から決まるときにその関係を関数と呼ぶことは、おそらく高等数学全体で最も重要な考え方である。読者がこの考え方をしっかり理解したと納得できるように、これから本章でたくさんの例を使って説明していく。
しかしその説明を始める前に、上に示した簡単な例が持つ次の三つの特徴が、一般的な関数という概念とは全く関係がない点を注意しておく必要がある:
- \(y\) は \(\bm{x}\) の全ての値に対して決定する。
- \(x\) の値それぞれに対して、ちょうど一つの \(\bm{y}\) の値が対応する。
- \(x\) と \(y\) の間の関係が解析的な式で表され、与えられた \(x\) の値に対応する \(y\) の値が変数の置換によって直接計算できる。
実を言えばこの三つの特徴は重要な関数の多くが持っている。しかし以降の例を見れば、これらの特徴が関数という概念に何ら本質的でないことが理解できるだろう。本質的なのは、何らかの形で \(x\) の値を \(y\) の値に結び付ける \(x\) と \(y\) の間の関係である。
-
\(y = x,\ y = 2x,\ y = \frac{1}{2}x,\ y = x^{2} + 1\) は関数である。こういった関数について今言っておくべきことはない。
-
\(x\) がどんな値であっても \(y = 0\) とする。このときどんな値が \(x\) として与えられたとしてもそれに対応する \(y\) の値 (つまり \(0\)) が分かるので、\(y\) は \(x\) の関数となる。この関数が表す関係では、全ての \(x\) の値に同じ \(y\) の値が対応する。\(y\) が \(0\) でなくて \(1,\ \frac{1}{2},\ \sqrt{2}\) だとしても同じことが言える。このような \(x\) の関数を定数 (constant) と呼ぶ。
-
\(y^{2} = x\) とする。\(x\) が正なら、この方程式は \(x\) の値それぞれに対応する \(y\) の値を二つ、具体的には \(±\sqrt{x}\) を定義する。また \(x = 0\) なら \(y = 0\) だから、\(0\) という \(x\) の値にはちょうど一つの \(y\) の値が対応する。そして \(x\) が負なら、方程式を満たす \(y\) の値は存在しない。つまり関数 \(y\) は \(x\) が負の値のとき定義されない。よってこの関数は特徴 (3) を持つが、(1) と (2) を持たない。
-
可動ピストンが上部に付いたシリンダーに閉じ込められた気体の体積を考える1。気体は定温とする。
ピストンの表面積を \(A\)、その重さを \(W\) とする。ピストンによって圧縮される気体は、ピストンに向かって単位面積当たり \(p_{0}\) の圧力を及ぼす。この圧力がピストンの重さ \(W\) と釣り合うので、次の式が成り立つ: \[ W = Ap_{0} \]
この系が平衡状態にあるときの気体の体積を \(v_{0}\) とする。ピストンの上に重りを追加すると、ピストンが下方向に及ぼす力が増加する。すると気体の体積 \(v\) が減少し、気体が及ぼす単位面積当たりのピストンへの圧力 \(p\) が増加する。ボイルが行った実験で得られた法則によって、\(p\) と \(v\) の積はほぼ定数であることが分かっている。これは次の等式として表せる: \[ pv = a \qquad \text{(i)} \] ここで \(a\) は実数であり、その近似値は実験で求められる。
しかしボイルの法則だけでは、気体がどこまでも圧縮され続けることはないという事実を詳しく説明できない。\(v\) の減少と \(p\) の増加が一定まで進むと、方程式 \(\mathrm{(i)}\) はもはや正確でなくなる。次の式で表される「ファンデルワールスの法則」を使うとずっと正確な近似を得られることが知られている: \[ \left(p + \frac{\alpha}{v^{2}}\right)(v - \beta) = \gamma \qquad \text{(ii)} \] ここで \(\alpha,\ \beta,\ \gamma\) は実数であり、その近似値は実験で求められる。
この二つの式が \(p\) と \(v\) の間の関係を完璧に表すわけではもちろんない。正確な関係は無論もっと入り組んでおり、\(v\) が変化するにしたがって \(\mathrm{(i)}\) に非常に近いものから \(\mathrm{(ii)}\) に非常に近いものまで変化する。しかし数学的な視点では、理想的な物質の状態を考えても構わない。つまり \(v\) がある値 \(V\) より大きいときは \(\mathrm{(i)}\) が正確に正しく、\(v\) が \(V\) より小さいときは \(\mathrm{(ii)}\) が正確に正しいとして構わない。そうすればこの二つの方程式が \(v\) の関数 \(p\) を定義するとみなせる。これは \(v\) の値の一部に対する値がとある式で定義され、他の \(v\) の値に対する値は別の式で定義される関数の例である。
この関数は特徴 (2) を持つ: 任意の \(v\) の値はちょうど一つの \(p\) の値に対応する。しかし特徴 (1) は持たない: \(v\) が負のときは \(p\) は \(v\) の関数として定義されない。「負の体積」は意味不明なので、負の \(v\) の値は最初から考えに入っていない。
-
完全弾性の球が (回転なしに) \(\frac{1}{2}g\tau^{2}\) の高さから水平な平面に落下し、何度も跳ね返るとする。
読者も知っているであろう初等力学の法則によると、\(h\) を時刻 \(t\) における初期位置から測った球の高さとしたとき、\(0 \leq t \leq \tau\) なら \(h = \frac{1}{2}gt^{2}\) となり、\(\tau \leq t \leq 3\tau\) なら \(h = \frac{1}{2}g(2\tau - t)^{2}\) となる。一般的には \((2n - 1)\tau \leq t \leq (2n + 1)\tau\) で \[ h = \frac{1}{2}g(2n\tau - t)^{2} \] が成り立つ。\(h\) は \(t\) の関数であり、正の \(t\) の値に対してのみ定義される。
-
\(y\) を \(\bm{x}\) の最大素因数と定義する。これは \(x\) の特定のクラスだけに適用される定義の例である。つまりこの定義は整数に対してのみ意味を持つ。「\(\frac{11}{3},\ \sqrt{2},\ \pi\) の最大素因数」は意味をなさないので、こうして定義される関係性は整数でない \(x\) に対応する値を定義できない。そのためこの関数は特徴 (1) を持たない。特徴 (2) は持つが、\(y\) を表す \(x\) の簡単な式は存在しないので特徴 (3) は持たない。
-
\(y\) を \(\bm{x}\) を既約分数にしたときの分母と定義する。これは \(x\) が有理数のときに限って定義される関数の例である。例えば \(x = -11/7\) なら \(y = 7\) だが、\(x = \sqrt{2}\) のとき \(y\) は定義されない。「\(\sqrt{2}\) の分母」は言葉の使い方として意味を持たない。
-
\(y\) を 1907 年 8 月 8 日午後 5:30 にロンドン市警察署の部署 \(\bm{C}\) にいる警察官 \(\bm{x}\) の背の高さ (インチ) と定義する。このとき \(y\) は特定の整数に対してのみ定義される。つまりこの時刻にこの場所にいる警察官の数を \(N\) とすると、\(x\) が \(1,\ 2,\ \ldots,\ N\) のときに限って \(y\) は値を持つ。
§21 関数の図示
変数 \(y\) が変数 \(x\) の関数だとする。この関数が表す \(x\) と \(y\) の関係を \(y\) の関数 \(x\) とみなすこともできるが、ここでは前者の視点に立って \(y\) を \(x\) の関数とみなして話を進める。このとき \(x\) を独立変数 (independent variable) と呼び、\(y\) を従属変数 (dependent variable) と呼ぶ。関数が表す関係が持つ形式が明らかでないときには、関数が存在するという事実を次の式で表す: \[ y = f(x) \] \(f(x)\) ではなく \(F(x),\ \phi(x),\ \psi(x),\ \ldots\) を使うこともある。
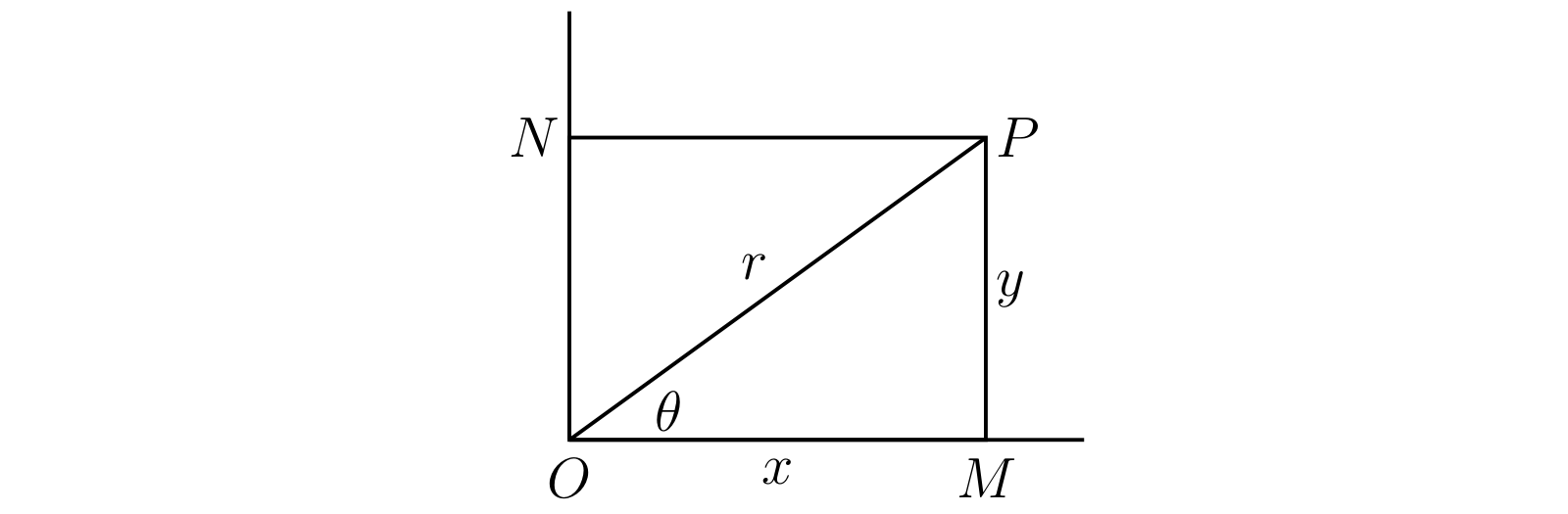
多くの場合で、関数の性質は次のように図示すると非常に分かりやすくなる。直行する二つの直線 \(OX,\ OY\) を両方向に無限に伸ばし、\(x\) と \(y\) の値をそれぞれ \(O\) から \(OX,\ OY\) に沿って測った長さで表す。もちろん符号を考慮し、図 6 のように正の方向に矢印を付ける。
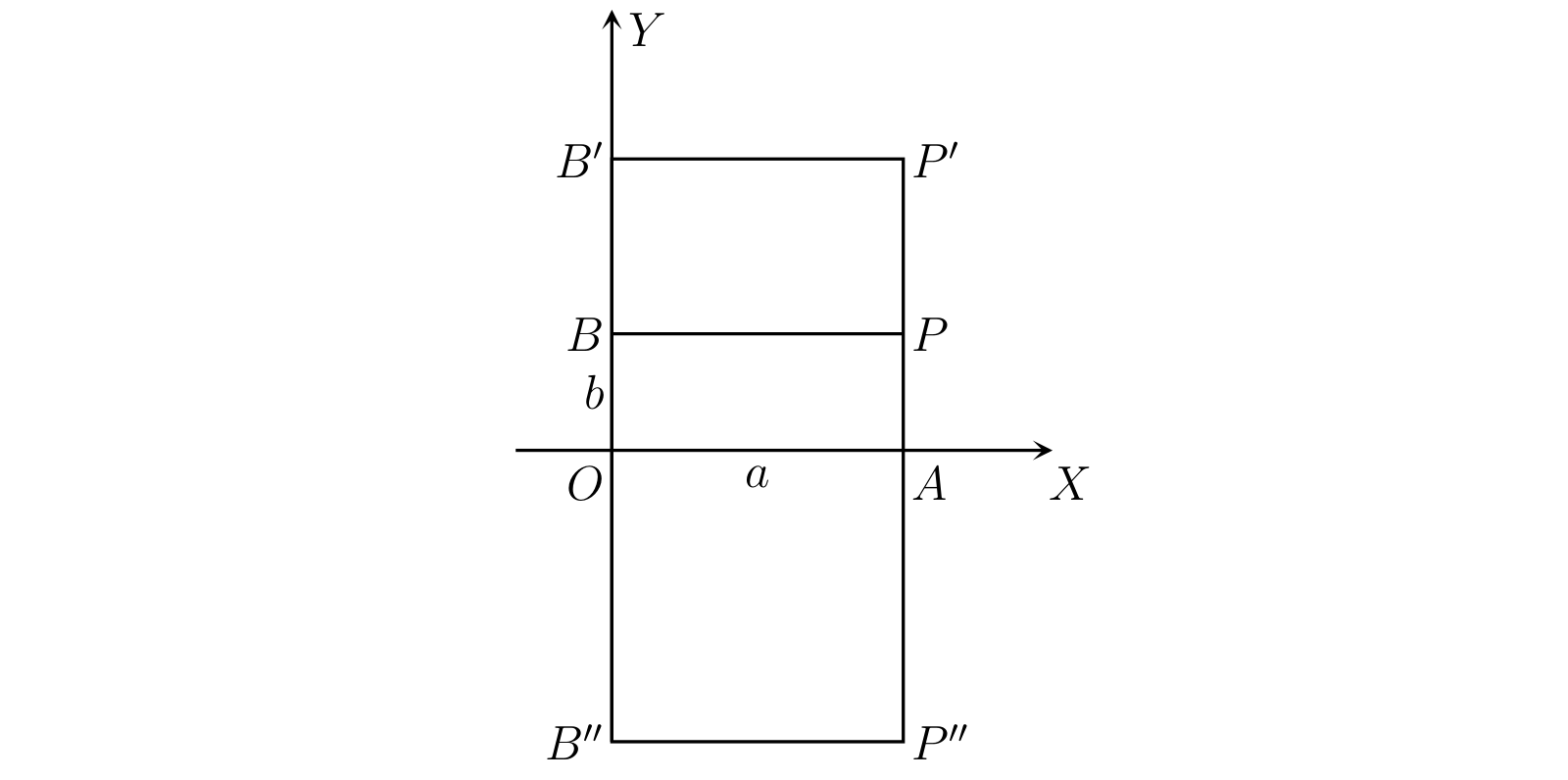
\(a\) を \(x\) の適当な値とし、\(a\) に対応する \(y\) の値 \(b\) が定義されているとする。\(OA = a\) と \(OB = b\) を取り、長方形 \(OAPB\) を描き、図中で \(P\) と印の付いた点を考える。このように印を付けた点 \(P\) は \(x = a\) に対する \(y\) の値が \(b\) であることを示しているとみなせる。
\(x\) の値 \(a\) が複数の \(y\) の値 (例えば \(b,\ b',\ b''\)) に対応するなら、一つの点 \(P\) の代わりに複数の点 \(P,\ P',\ P''\) が取れる。
\(P\) を点 (point) \((a, b)\) と呼び、\(a\) と \(b\) を軸 \(OX,\ OY\) に沿った \(P\) の座標 (coordinate) と呼ぶ。\(a\) は \(P\) の横座標 (abscissa) であり、\(b\) は \(P\) の縦座標 (ordinate) である。\(OX\) と \(OY\) はそれぞれ \(x\) 軸 (axis of \(x\)) および \(y\) 軸 (axis of \(y\)) と呼び、両方まとめて座標軸 (axis of coordinate) と呼ぶ。\(O\) は座標原点 (origin of coordinate) あるいは原点 (origin) と呼ばれる。
\(y\) の値 \(b\) (あるいは \(b,\ b',\ b'',\ \ldots\)) が定義される全ての \(x\) の値 \(a\) に対応する点 \(P\) (あるいは \(P,\ P',\ P'',\ \ldots\)) が定まったとする。それらの点全ての集まりを関数 \(y\) のグラフ と呼ぶ。
非常に簡単な例として、\(y\) が次の方程式で定義される \(x\) の関数である場合を考える: \[ Ax + By + C = 0 \qquad \text{(1)} \] ここで \(A,\ B,\ C\) は固定された実数とする2。このとき \(y\) は \(x\) の関数であり、§20 で示した三つの特徴を全て持つ。そして \(\bm{y}\) のグラフが直線であることは容易に示せる。この命題の証明は解析幾何学の教科書に載っているし、読者もいくつか知っているだろう。
異なる表現を使うこともある。つまり「\(x\) と \(y\) が方程式 (1) を満たしならが動くとき、点 \(\bm{(x, y)}\) の軌跡が直線になる」と言うことがある。このとき方程式 (1) を軌跡の方程式と呼び、この方程式が軌跡を表すと表現する。この「軌跡」や「軌跡の方程式」という言葉は非常によく使われ、\(x\) と \(y\) の関係が解析的な式で表せるときにはいつでも考えられる。
\(Ax + By + C\) は一次より大きい項が含まれない最も一般的な \(x\) と \(y\) の多項式なので、方程式 \(Ax + By + C = 0\) は一般的な一次方程式である。つまり一般的な一次方程式は直線を表す。これと逆の命題「直線の方程式は一次方程式である」も簡単に示せる。
興味深い幾何学的な軌跡をさらにいくつか示す。方程式 \[ (x - \alpha)^{2} + (y - \beta)^{2} = \rho^{2} \] および \[ x^{2} + y^{2} + 2Gx + 2Fy + C = 0, \] はどちらも円を表す。ただし二番目の方程式では \(G^{2} + F^{2} - C \gt 0\) とする。また \[ Ax^{2} + 2Hxy + By^{2} + 2Gx + 2Fy + C = 0 \] (一般的な二次方程式) は、係数が特定の不等式を満たすという条件の下で、円錐曲線 (楕円・放物線・双曲線) を表す。こういった軌跡に関するさらなる議論は解析幾何学の本に譲る。
§22 極座標
前節では \(P\) の座標の大きさ \(OM = x\) と \(MP = y\) で \(P\) の位置を特定した。\(OP = r\) および \(\angle MOP = \theta\) として、\(\theta\) は (正の方向に測って) \(0\) から \(2\pi\) だとする。このとき \[ \begin{aligned} x & = r\cos\theta, \quad y & = r\sin\theta, \quad r & = \sqrt{x^{2} + y^{2}}, \quad \cos\theta : \sin\theta : 1 & = x : y : r \end{aligned} \] が成り立ち、\(r\) と \(\theta\) からも \(P\) の位置を決定できると分かる。加えて\(r\) は必ず \(0\) 以上となる3。
\(P\) がとある軌跡上を動くなら、\(r\) と \(\theta\) の間には関係が生まれる。これを \(r = f(\theta)\) あるいは \(\theta = F(r)\) と表記し、軌跡の極方程式 (polar equation) と呼ぶ。上記の関係を使えば極方程式を \((x, y)\) の方程式から求められる (逆もできる)。
例えば直線の極方程式は次の形をしていると示せる: \[ r\cos(\theta - \alpha) = p \] ここで \(p\) と \(\alpha\) は定数である。また方程式 \(r = 2a\cos\theta\) は原点を通る円を表す。この方程式は定数 \(A,\ c,\ \alpha\) を使った \[ r^{2} + c^{2} - 2rc\cos(\theta - \alpha) = A^{2} \] から得られる。
§23 多項式
これからの例を見れば、無限に存在する様々な種類の関数をよりよく理解できるだろう。
-
多項式: 次の形をした関数を \(x\) の多項式 (polynomial) と呼ぶ: \[ a_{0}x^{m} + a_{1}x^{m-1} + \cdots + a_{m} \] ここで \(a_{0},\ a_{1},\ \ldots,\ a_{m}\) は定数を表す。もっとも単純な多項式は \(x\) のべき乗 \(y = x,\ x^{2},\ x^{3},\ \ldots,\ x^{m},\ \ldots\) であり、\(x^{m}\) のグラフは \(m\) の偶奇によって二つに分かれる。
まず \(m = 2\) の場合を考える。このとき三つの点 \((0, 0),\ (1, 1),\ (-1, 1)\) はグラフ上にある。グラフ上のその他の点は \(x\) に特定の値を代入すれば得られる。例えば \[ x = \frac{1}{2},\quad 2,\quad 3,\quad -\frac{1}{2},\quad -2,\quad 3 \quad \] のとき、それぞれ \[ y = \frac{1}{4},\quad 4,\quad 9,\quad \hphantom{-}\frac{1}{4},\quad \hphantom{-}4,\quad 9 \quad \] となる。グラフ上の点をいくつかプロットすれば、グラフ全体が 図 8 のような形をしていると予想できる。グラフ上にあると分かった点を結んで曲線を描き、適当な別の \(x\) とそれに対応する \(y\) をプロットしてその正確さをテストすれば、新しい点が曲線にとても近いことが分かるだろう (手で書いた分だけ不正確にはなる)。この曲線はもちろん放物線である。
しかしここで、現段階では正確に答えられない重要な問題が一つある。読者も聞いたことがあるであろう連続曲線 (continuous couve) という言葉についてである。連続曲線と言えば値が飛んだりしない繋がった曲線のことであり、例えば 図 8 にある曲線は連続曲線に見える。問題は、関数 \(y = x^{2}\) のこのグラフが本当に連続曲線かどうかである。曲線上の点を個別にたくさん計算すれば見た目は連続らしく見えるが、これは証明ではない。
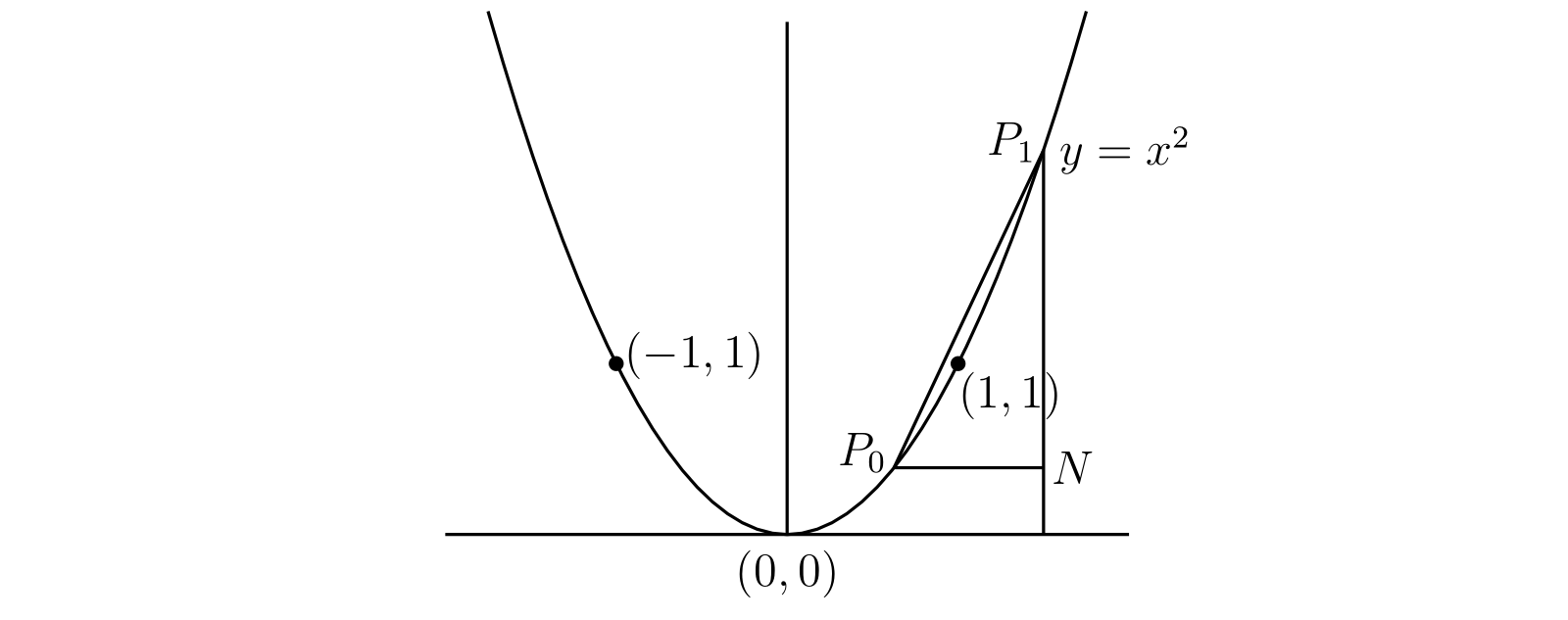 図 8
図 8この問題は第五章まで議論できない。第五章では私たちが普通に使う「連続」という言葉の正確な意味を正確に議論し、上述のグラフおよびこの章でこれから考えるいくつかのグラフが確かに連続なことを証明する。なので今のところは、関数のグラフを「常識的に」描いてもらって構わない。
\(y = x^{2}\) が いたるところで \(x\) 軸に対して凸なことは簡単に示せる。\(P_{0},\ P_{1}\) を \((x_{0}, x_{0}^{2}),\ (x_{1}, x_{1}^{2})\) とする (図 8 参照)。このとき弦 \(P_{0}P_{1}\) 上にある点の座標は、和が \(1\) である二つの正の実数 \(\lambda\) と \(\mu\) を使って \(x = \lambda x_{0} + \mu x_{1},\ y = \lambda x_{0}^{2} + \mu x_{1}^{2}\) と表せる。さらに \[ \begin{aligned} y - x^{2} & = (\lambda + \mu)(\lambda x_{0}^{2} + \mu x_{1}^{2}) - (\lambda x_{0} + \mu x_{1} )^{2} \\ & = \lambda\mu(x_{1} - x_{0})^{2} \geq 0 \end{aligned} \] が成り立つから、この弦は完全に曲線の上にある。
曲線 \(y = x^{4}\) は全体的に \(y = x^{2}\) と似ているが、\(O\) の近くではより緩やかであり、図 9 中の \(A,\ A'\) を超えるとより急になる。そして \(4\) より大きい偶数 \(m\) に対してはこの性質がさらに顕著になる。\(m\) が大きくなると緩やかな部分と急な部分がさらに強調され、最終的に見た目では図中の太い線と区別できなくなる。
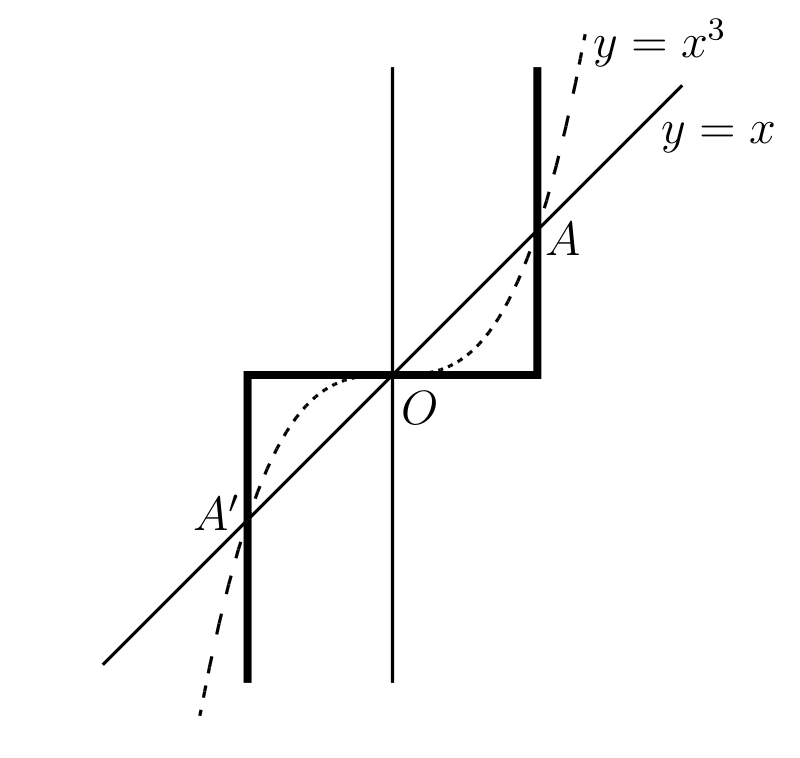
次に奇数 \(m\) に対する \(y = x^{m}\) のグラフを考える。二つのグラフの重要な違いは、\(m\) が偶数のときは \((-x)^{m} = x^{m}\) なのでグラフが \(OY\) に関して対称となるのに対して、\(m\) が奇数のときは \((-x)^{m} = -x^{m}\) なので \(x\) が負のとき \(y\) が負となる点にある。図 10 に曲線 \(y = x\) と \(y = x^{3}\) を示す。太線は大きな奇数の \(m\) に対する \(y = x^{m}\) を近似した曲線である。
ここまでくれば、任意の多項式のグラフを (いくらか理論的に) 描くことができる。まず \(y = x^{m}\) のグラフがあれば、全ての点の縦座標を \(C\) 倍することで \(y = Cx^{m}\) のグラフが得られる (\(C\) は整数)。次にもし \(f(x)\) と \(F(x)\) のグラフがあれば、全ての点に対して二つのグラフの縦座標の和をとることで \(f(x) + F(x)\) のグラフが得られる。
しかし多項式のグラフの描画にはもっと簡単な微積分を使った方法がある。この方法は後で説明するので、この話題はここまでとする。
-
曲線 \(y = 7x^{4},\ y = 3x^{5},\ y = x^{10}\) の通る点を調べよ。
[三つのグラフは一つの図に注意深く描くこと4。\(x\) の項が持つ最大の指数が大きいと、\(x\) が大きくなるにしたがって値が急速に大きくなることが分かるだろう。また \[ x^{10} + 3x^{5} + 7x^{4} \] といった多項式では (あるいは \(x^{10} + 30x^{5} + 700x^{4}\) でさえ)、\(x\) が大きいときに大部分を占めるのは最初の項である。\(x = 4\) のときでさえ \(x^{10} \gt 1,000,000\) であり、このとき \(30x^{5} \lt 35,000\) および \(700x^{4} \lt 180,000\) に過ぎない。\(x = 10\) ともなれば最初の項はさらに大きくなる]
-
\(x = 1,\ 10,\ 100\) といった値で \(x^{12},\ 1,000,000x^{6},\ 1000,000,000,000x\) の相対的な大きさを比較せよ。
[同じような例を他にも作ってみるとよい。関数の相対的な増加速度という考え方はこれから何度も出てくる]
-
\(ax^{2} + 2bx + c\) のグラフを描け。
[\(y - \{(ac - b^{2})/a\} = a\{x + (b/a)\}^{2}\) だから、点 \((-b/a, (ac - b^{2})/a)\) を通る新しい軸を元の軸と平行に取れば、この方程式は新しい軸における \(y' = a{x'}^{2}\) となる。この曲線は放物線である]
-
曲線 \(y = x^{3} - 3x + 1,\ y = x^{2}(x - 1),\ y = x(x - 1)^{2}\) が通る点を調べよ。
§24 有理関数 (その 1)
-
簡単で重要な関数のクラスとしては有理関数 (rational function) が多項式に続く。有理関数は二つの多項式の商であり、一般的には多項式 \(P(x),\ Q(x)\) を使って次のように表せる: \[ R(x) = \frac{P(x)}{Q(x)} \]
\(Q(x)\) が \(1\) あるいは定数 (\(x\) が関係しない式) となる特別なケースでは、\(R(x)\) が多項式となる。つまり有理関数は部分クラスとして多項式を含む。定義に関して注意すべき点をあげる:
-
\(P(x)\) と \(Q(x)\) に共通因数 \(x + a\) あるいは \(x^{p} + ax^{p-1} + bx^{p-2} + \cdots + k\) がないことを通常は仮定する。つまり共通因数は除算によって全て削除されているとする。
-
ただし共通因数を削除すると一般的に言って関数が変化することに気を付けなければならない。例えば関数 \(x/x\) は有理関数であり、共通因数を削除すると \(1/1 = 1\) を得る。しかし \(x/x\) と \(1\) は常に等しいわけではない。等しくなるのは \(x \neq 0\) のときだけであり、\(x = 0\) のとき \(x/x\) は \(0/0\) となって意味をなさなくなる。つまり \(x/x\) は \(x \neq 0\) のとき \(1\) に等しく、\(x = 0\) のときには定義されない。そのため関数としては \(1\) と等しくない。関数 \(1\) は常に \(1\) に等しい。
-
関数 \[ \left(\frac{1}{x + 1} + \frac{1}{x - 1}\right) \bigg/ \left(\frac{1}{x} + \frac{1}{x - 2}\right) \] は通常の代数法則で次の形に簡略化できる: \[ \frac{x^{2}(x - 2)}{(x - 1)^{2} (x + 1)} \] これは標準的な形の有理関数だが、ここでもこの簡略化が常には正しくないことに注意する必要がある。ある \(x\) の値に対する関数の値を計算するには、与えられた形の関数の \(x\) を置き換えなければならない。与えられた形の関数は \(x = -1,\ 1,\ 0,\ 2\) のとき意味のない形となるので、これらの \(x\) の値に対応する関数の値は定義されない。簡略化された式は \(x = -1\) と \(x = 1\) で定義されないが、\(x = 0\) と \(x = 2\) では \(0\) になる。よってここでも二つの関数は等しくない。
-
(3) の例のように、標準形の有理関数でも特定の \(x\) に対しては値が定義されないことがある。具体的には分母が \(0\) になる \(x\) があるなら、関数はその \(x\) に対して定義されない、例えば有理関数 \((x^{2} - 7)/(x^{2} - 3x + 2)\) では \(x = 1\) と \(x = 2\) で定義されない。
-
これから (2) や (3) で考えたような形の式を考えるときは、単純化が間違った意味を持ってしまう特別な \(x\) の値を無視して、有理関数の標準形まで単純化してしまうことにする。容易に確認できるように、この理解の下では二つの有理関数の和、積、商がどれも有理関数の標準系まで単純化できる。さらに一般に有理関数の有理関数は有理関数になる。つまり \(z = P(y)/Q(y)\) に対して \(y = P_{1}(x)/Q_{1}(x)\) を代入したとしても、単純化によって \(z = P_{2}(x)/Q_{2}(x)\) の形が得られる (\(P_{1},\ P_{2},\ Q_{1},\ Q_{2}\) は全て多項式を表す)。
-
有理関数の定義では、係数部分の定数が有理数だとは指定されていない。「有理」という言葉は関数における変数 \(x\) の登場の仕方だけを示している。そのため例えば \[ \frac{x^{2} + x + \sqrt{3}}{x\sqrt[3]{2} - \pi} \] は有理関数となる。
有理という言葉が使われる理由は次の通りである。有理関数 \(P(x)/Q(x)\) は \(x\) に対する有限回の操作だけで得られる。つまり \(x\) とそれ自身または定数との乗算、その乗算結果の加算、その乗算および加算結果の除算という操作であり、これは \(1\) から有理数を作る操作によく似ている。次の式で表される操作である: \[ \frac{5}{3} = \frac{1 + 1 + 1 + 1 + 1}{1 + 1 + 1} \]
繰り返しになるが、上述の操作で手に入る \(x\) の関数に対してさらに同種の操作を行って得られる任意の関数は、有理関数の標準形に単純化できる。次の例を見れば、この方法で手に入る一般的な関数がどのようなものか理解できるだろう: \[ \Biggl(\frac{x}{x^{2} + 1} + \frac{2x + 7}{x^{2} + \dfrac{11x - 3\sqrt{2}}{9x + 1}}\Biggr) \Bigg/ \left(17 + \frac{2}{x^{3}}\right) \] これはもちろん有理関数の標準形に単純化できる。
-
§25 有理関数 (その 2)
有理関数のグラフの描画では、多項式よりもさらに増して微積分の方法が有用になる。そのためここでは例をほんの少し示すに留める。
-
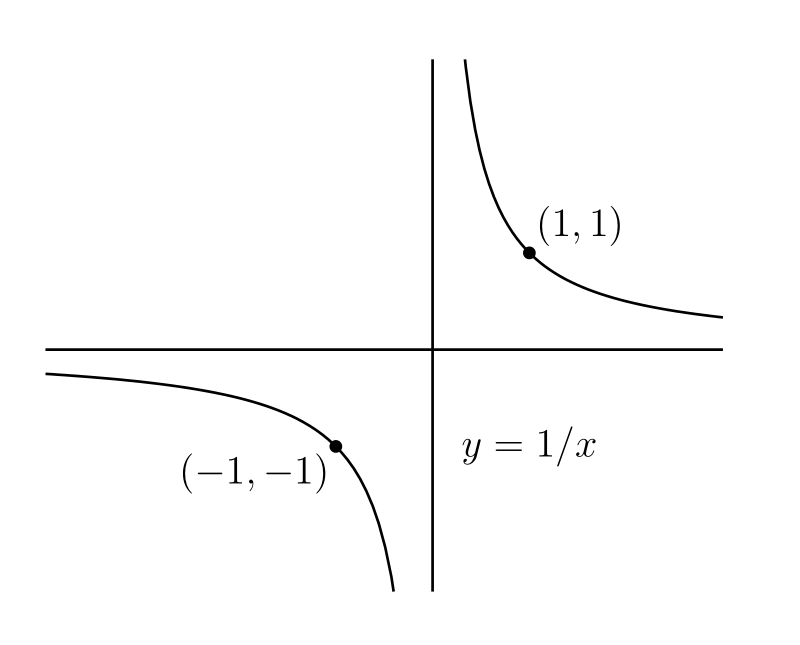
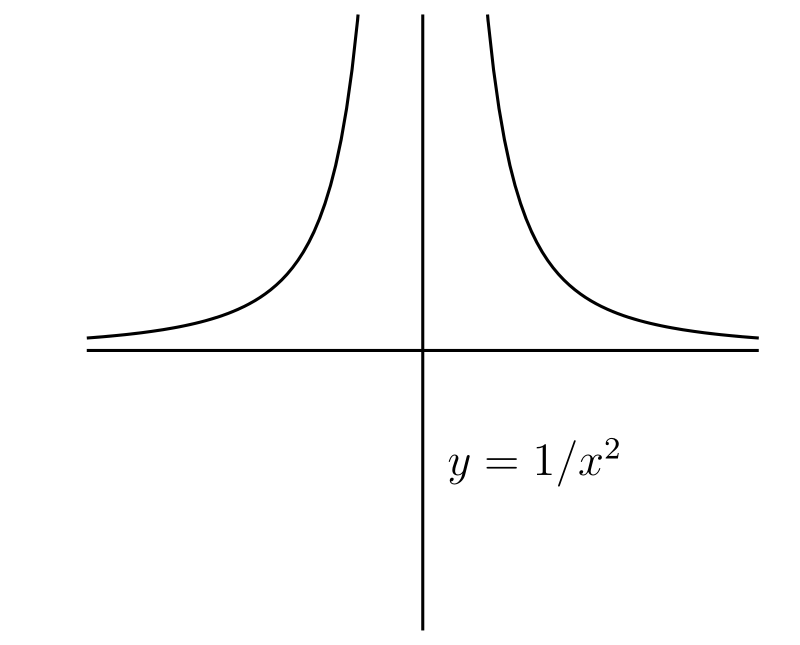
\(y = 1/x,\ y = 1/x^{2},\ y = 1/x^{3},\ \ldots\) のグラフを描け。
[最初の二つの関数のグラフを次の図に示す。\(1/0,\ 1/0^{2},\ \ldots\) といった表現は意味をなさないので、これらの関数は \(x = 0\) で定義されないことに注意してほしい]
-
\(y = x + (1/x),\ x - (1/x),\ x^{2} + (1/x^{2}),\ x^{2} - (1/x^{2}),\ ax + (b/x)\) が通る点を調べよ。正の値、負の値、\(a,\ b\) など様々な値を試すこと。
-
次の関数の通る点を調べよ: \[ y = \frac{x + 1}{x - 1},\quad \left(\frac{x + 1}{x - 1}\right)^{2},\quad \frac{1}{(x - 1)^{2}},\quad \frac{x^{2} + 1}{x^{2} - 1} \]
-
\(y = 1/(x - a)(x - b),\ 1/(x - a)(x - b)(x - c)\) の通る点を調べよ。ただし \(a \lt b \lt c\) とする。
-
\(m\) が極端に大きいときの曲線 \(y = 1/x^{m}\) の一般的な形を示せ。\(m\) が偶数の場合と奇数の場合を分けて考えること。
§26 陽な代数関数
-
次に考える重要な関数のクラスは陽な代数関数 (explicit algebraical function) のクラスである。このクラスは、有理関数を作るのに使った操作に加えて根号を取る操作を \(x\) に対して有限回行って得られる関数から構成される。例えば \[ \frac{\sqrt{1 + x} - \sqrt[3]{1 - x}} {\sqrt{1 + x} + \sqrt[3]{1 - x}},\quad \sqrt{x} + \sqrt{x +\sqrt{x}},\quad \left(\frac{x^{2} + x + \sqrt{3}}{x\sqrt[3]{2} - \pi}\right)^{\frac{2}{3}} \] および整数 \(m,\ n\) に対する \(x^{m/n}\) (\(= \sqrt[n]{x^{m}}\)) はどれも陽な代数関数である。
\(y = \sqrt{x}\) といった関数の意味に曖昧さがあることを注意しておく。ここまでは \(\sqrt{2}\) で \(2\) の正の平方根を意味してきた。直感的にはこうして \(\sqrt{x}\) で正の数 \(x\) の正の平方根を表すとした方が自然であり、この場合 \(\sqrt{x}\) は \(x\) の一価関数となる。ただし \(\sqrt{x}\) を正負の根号も表す多価関数とみなした方が便利な場合もある。
ここまで進んだ時点で、読者は \(\sqrt{x}\) という関数が二つの点で有理関数と大きく異なることに気が付くだろう。まず、孤立した単一の点を除けば全ての \(x\) で定義された有理関数と違い、\(\sqrt{x}\) は \(x\) のとある範囲全体 (具体的には負の値全体) で定義されない。次に、値が定義される \(x\) に対して \(\sqrt{x}\) は逆の符号を持つ二つの値がある。
一方で \(\sqrt[3]{x}\) は一価関数であり、全ての \(x\) に対して定義される。
-
\(a \lt b\) とすると、\(\sqrt{(x - a)(b - x)}\) は \(a \leq x \leq b\) に対してしか定義されない。そして \(a \lt x \lt b\) ならこの関数は二つの値を持つ。\(x = a\) または \(x = b\) なら値は \(0\) だけとなる。
-
次の関数に対して同様の考察をせよ: \[ \sqrt{(x - a)(x - b)(x - c)} \quad (a \lt b \lt c), \] \[ \sqrt{x(x^{2} - a^{2})},\quad \sqrt[3]{(x - a)^{2}(b - x)}\quad (a \lt b), \] \[ \frac{\sqrt{1 + x} - \sqrt{1 - x}} {\sqrt{1 + x} + \sqrt{1 - x}},\quad \sqrt{x + \sqrt{x}} \]
-
曲線 \(y^{2} = x,\ y^{3} = x,\ y^{2} = x^{3}\) が通る点を調べよ。
-
次の関数のグラフを描け: \[ y = \sqrt{a^{2} - x^{2}},\quad y = b\sqrt{1 - (x^{2}/a^{2})} \]
§27 陰な代数関数
-
もし \[ y = \frac{\sqrt{1 + x} - \sqrt[3]{1 - x}} {\sqrt{1 + x} + \sqrt[3]{1 - x}} \] なら、次の関係が容易に分かる: \[ y = \sqrt{x} + \sqrt{x + \sqrt{x}} \] あるいはもし \[ y = \sqrt{x} + \sqrt{x + \sqrt{x}} \] なら、次が成り立つ: \[ y^{4} - (4y^{2} + 4y + 1)x = 0 \] この二つの方程式は、どれも次の形をしている; \[ y^{m} + R_{1}y^{m-1} + \cdots + R_{m} = 0 \qquad \text{(1)} \] ここで \(R_{1},\ R_{2},\ \ldots,\ R_{m}\) は \(x\) の有理関数である。\(y\) をこれまでの例で考えた関数とすれば、\(y\) がこの形の方程式を満たすことは簡単に分かる。さらに任意の陽な代数関数についても同様だろうと自然に予想できる。この予想は正しく、証明も難しくないが、きちんとした証明を書くのに時間は割かないことにする。例を一つ示せば、証明がどのように進むかは理解できるだろう: \[ y = \frac{x + \sqrt{x} + \sqrt{x + \sqrt{x}} + \sqrt[3]{1 + x}} {x - \sqrt{x} + \sqrt{x + \sqrt{x}} - \sqrt[3]{1 + x}} \] とすると、次の式を得る: \[ y = \frac{x + u + v + w} {x - u + v - w}, \] \[ u^{2} = x,\quad v^{2} = x + u,\quad w^{3} = 1 + x \] 求めたい形の方程式を得るには、これらの方程式から \(u,\ v,\ w\) を削除すればよい。
以上の考察から、代数関数の定義 「関数 \(y = f(x)\) が \(x\) の代数関数 (algebraical function) であるとは、\(y\) が (1) の形をした方程式の根である、つまり \(x\) の有理関数を係数に持つ \(y\) の \(m\) 次方程式の根であることを言う」が導かれる。明らかに、方程式の最初の係数が \(1\) であると仮定しても一般性は失われない。
この関数のクラスは §26 で考えた陽な代数関数を全て含む。しかし、陽な代数関数として表せない関数もこのクラスには含まれる。一般的に言って \(m\) が \(4\) より大きいときの方程式 (1) は、\(y\) について \(x\) の式として陽に解くことができない。もちろん \(m = 1,\ 2,\ 3,\ 4\) では陽な解が存在し、\(m\) が大きくても陽な解が存在する特殊な場合もある。
代数関数の定義を前章で示した代数的数の定義と比較するとよい。
-
\(m = 1\) なら、\(y\) は有理関数である。
-
\(m = 2\) なら (1) の方程式は \(y^{2} + R_{1}y + R_{2} = 0\) であり、 \[ y = \frac{1}{2}\left(-R_{1} ± \sqrt{R_{1}^{2} - 4R_{2}}\right) \] となる。この関数は \(R_{1}^{2} \geq 4R_{2}\) となる全ての \(x\) の値に対して定義される。\(R_{1}^{2} \gt 4R_{2}\) のときこの関数は二つの値を持ち、\(R_{1}^{2} = 4R_{2}\) のときには一つの値を持つ。
\(m = 3,\ 4\) の場合には、代数の文献にある方法を使って三次方程式および四次方程式を解くことになる。ただしこの処理は複雑で式の形も扱いづらいので、最初の方程式を使った方が関数の性質を簡単に調べられることが多い。
-
次の方程式が定義する関数を考える: \[ y^{2} - 2y - x^{2} = 0,\quad y^{2} - 2y + x^{2} = 0,\quad y^{4} - 2y^{2} + x^{2} = 0 \] いずれの場合でも \(y\) を \(x\) の陽な関数として書くことができ、それを見れば関数の定義される \(x\) の値が分かる。
-
次の関数それぞれについて、関数が満たす \(x\) の有理式を係数に持つ代数方程式を示せ: \[ \sqrt{x} + \sqrt{1/x},\quad \sqrt[3]{x} + \sqrt[3]{1/x},\quad \sqrt{x + \sqrt{x}},\quad \sqrt{x + \sqrt{x + \sqrt{x}}} \]
-
方程式 \(y^{4} = x^{2}\) を考えよ。
[まず \(y^{2} = ±x\) が分かり、ここから \(x\) が正なら \(y = \sqrt{x}\) で、\(x\) が負なら \(y = \sqrt{-x}\) が分かる。よってこの関数は \(x = 0\) 以外の全ての値に対して二つの値を持つ]
-
\(x\) の代数関数の代数関数もまた \(x\) の代数関数である。
[仮定から次が成り立つ: \[ y^{m} + R_{1}(z)y^{m-1} + \cdots + R_{m}(z) = 0 \] ここで \[ z^{n} + S_{1}(x)z^{n-1} + \cdots + S_{n}(x) = 0 \] である。\(z\) を削除すれば次の式が得られる: \[ y^{p} + T_{1}(x)y^{p-1} + \cdots + T_{p}(x) = 0 \] 大文字は全て有理関数を表す]
-
代数的な形で陽に表せない関数の例を示しておくべきだろう。次の方程式を満たす関数 \(y\) がそのような例である: \[ y^{5} - y - x = 0 \] しかし \(y\) を代数的な形で陽に表せないことの証明は難しいので、ここでは示さない。
§28 超越関数
有理関数でなく代数関数でさえない関数は全て超越関数 (transcendental function) と呼ばれる。否定的に定義されるこの関数のクラスには無限の種類の様々な関数が当然含まれ、その中には単純な関数もあれば重要な関数もある。そういった中で今の私たちが理解できる特に興味深い関数が二種類ある。
-
三角関数とその逆関数: これは初等三角法で使われるサイン関数とコサイン関数およびそれらの逆関数のことである。読者はこういった関数の基本的な性質を知っているものと仮定する5。
-
\(\cos x,\ \sin x\) および \(a\cos x + b\sin x\) のグラフを描け。
[サインとコサインがそれぞれ \(a/\sqrt{a^{2} + b^{2}}\) と \(b/\sqrt{a^{2} + b^{2}}\) である値を \(\alpha\) とし、さらに \(\beta = \sqrt{a^{2} + b^{2}}\) とすれば、\(a\cos x + b\sin x = \beta\cos(x - \alpha)\) が成り立つ。そのため三つの関数のグラフは相似である]
-
\(\cos^{2} x,\ \sin^{2} x,\ a\cos^{2} x + b\sin^{2} x\) のグラフを描け。
-
\(f(x)\) と \(F(x)\) のグラフが描かれているとする。このとき \[ f(x)\cos^{2} x + F(x)\sin^{2} x \] のグラフは \(y = f(x)\) と \(y = F(x)\) の間を揺れ動く曲線となる。\(f(x) = x,\ F(x) = x^{2}\) のときのグラフを描け。
-
\(\cos px + \cos qx\) のグラフが \(2\cos\frac{1}{2}(p - q)x\) と \(-2\cos\frac{1}{2}(p + q)x\) のグラフの間にあり、二つのグラフに交互に接することを示せ。\((p - q)/(p + q)\) が小さい場合のグラフの概形を描け。
(Math. Trip. 1908.)
-
\(x + \sin x,\ \ \dfrac{1}{x} + \sin x,\ \ x\sin x,\ \ \dfrac{\sin x}{x}\) のグラフを描け。
-
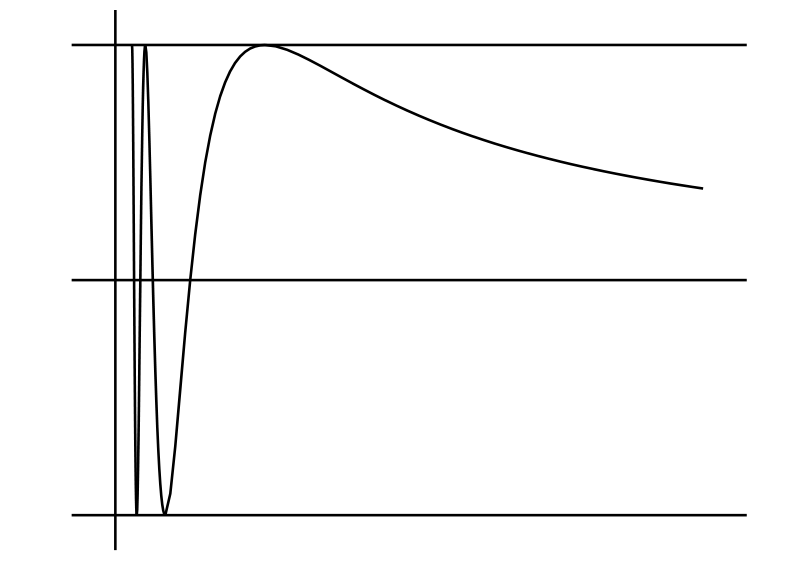
\(\sin\dfrac{1}{x}\) のグラフを描け。 [\(y = \sin(1/x)\) とすると任意の整数 \(m\) に対して \(x = 1/m\pi\) で \(y = 0\) となる。同様に \(x = 1/(2m + \frac{1}{2})\pi\) なら \(y = 1\)、\(x = 1/(2m - \frac{1}{2})\pi\) なら \(y = -1\) である。この曲線は全体が \(y = -1\) と \(y = 1\) の間に収まる (図 13)。グラフは上下に振動し、そのスピードは \(x\) が \(0\) に近づくにつれて速くなる。\(x = 0\) では関数が定義されない。また \(x\) が大きいとき \(y\) は小さくなる6。曲線の負の部分は正の部分と相似である]
-
\(x\sin\dfrac{1}{x}\) のグラフを描け。
[前問の曲線が \(y = -1\) と \(y = 1\) の間にあったのと同様に、この曲線は \(y = -x\) と \(y = x\) の間にある (図 14)]
-
次の関数のグラフを描け: \[ x^{2}\sin \frac{1}{x},\quad \frac{1}{x}\sin \frac{1}{x},\quad \sin^{2} \frac{1}{x},\quad \left\{x\sin \frac{1}{x}\right\}^{2}, \] \[ \quad a\cos^{2} \frac{1}{x} + b\sin^{2} \frac{1}{x}, \quad \sin x + \sin \frac{1}{x},\quad \sin x\sin \frac{1}{x} \]
-
次の関数のグラフを描け: \[ \cos x^{2},\ \sin x^{2},\ a\cos x^{2} + b\sin x^{2} \]
-
\(\arccos x\) と \(\arcsin x\) のグラフを描け。
[\(y = \arccos x\) なら \(x = \cos y\) が成り立つ。この関係から、\(y\) の関数 \(x = \cos y\) のグラフから \(x\) の関数 \(y = \arccos x\) のグラフが得られると分かる。明らかに \(y\) は \(-1 \leq x \leq 1\) でのみ定義され、この \(x\) に対して無限個の値を持つ。つまり \(-1 \lt x \lt 1\) に対する \(0\) と \(\pi\) の間の \(y\) の値を \(\alpha\) すれば、他の \(y\) の値は \(n\) を (正負を問わない) 任意の整数として \(2n\pi ± \alpha\) となる]
-
次のグラフを描け: \[ \tan x,\quad \cot x,\quad \sec x, \quad \cosec x,\quad \tan^{2} x,\quad \cot^{2} x, \quad \sec^{2} x,\quad \cosec^{2} x \]
-
\(\arctan x,\ \operatorname{arccot} x,\ \operatorname{arcsec} x,\ \operatorname{arccosec} x\) のグラフを描け。特定の一つの値から他の関数の全ての値を表す (問題 10 で示したような) 式を示せ。
-
\(\tan \dfrac{1}{x},\ \cot \dfrac{1}{x},\ \sec \dfrac{1}{x},\ \cosec \dfrac{1}{x}\) のグラフを描け。
-
\(\cos x\) と \(\sin x\) が \(x\) の有理関数でないことを示せ。
[\(f(x)\) が定義される全ての \(x\) に対して \(f(x) = f(x + a)\) が成り立つとき、関数 \(f\) は周期的 (perdiodic) であると言い、\(a\) をその周期 (period) と呼ぶ。\(\cos x\) と \(\sin x\) は周期 \(2\pi\) の周期関数である。定数でない有理関数が周期関数でないことは次の通り簡単に示せる。\(P\) と \(Q\) が多項式で \[ f(x) = \frac{P(x)}{Q(x)} \] と仮定し、全ての \(x\) で \(f(x) = f(x + a)\) とする。\(f(0) = k\) と置くと、方程式 \(P(x) - kQ(x) = 0\) は \(x = 0,\ a,\ 2a,\ \ldots\) という無限に多くの \(x\) で満たされる。したがってこの方程式は全ての \(x\) で成り立ち、\(f(x) = k\) すなわち \(f(x)\) は定数である]
-
より一般的に、周期を持つ関数は \(x\) の代数関数でないことを示せ。
[代数関数を定義する方程式を \[ y^{m} + R_{1}y^{m-1} + \cdots + R_{m} = 0 \qquad \text{(1)} \] とする。ここで \(R_{1},\ \ldots\ \) は \(x\) の有理関数である。これを変形すると、\(x\) の多項式 \(P_{0},\ P_{1},\ \ldots\ \) を使って \[ P_{0}y^{m} + P_{1}y^{m-1} + \cdots + P_{m} = 0, \] となる。前問と同様の議論により \[ P_{0}k^{m} + P_{1}k^{m-1} + \cdots + P_{m} = 0 \] が全ての \(x\) について成り立つ。よって \(y = k\) とすれば (1) が全ての \(x\) について満たされる。すなわち今考えている代数関数の値の一つは定数に単純化される。
さらに (1) を \(y - k\) で割って同じ議論を繰り返す。すると私たちが考えている代数関数は全ての \(x\) について \(k,\ k',\ \ldots\) という定数値しかとらない、つまりこの関数はいくつかの定数値からなることが最終的に結論できる]
-
サインとコサインの逆関数は有理関数でも代数関数でもない。 [\(-1\) と \(1\) の間の任意の \(x\) に対する \(\arcsin x\) と \(\arccos x\) の値が無限個あることから示せる]
§29 その他の超越関数
-
三角関数に次いで重要なのが、指数関数と対数関数である。これらの関数は第九章と第十章で取り上げるが、今の私たちには手に余る。また性質が調べられているその他の超越関数、例えば楕円関数・ベッセル関数・ラグランジュ関数・ガンマ関数はどれもこの本の範囲を超える。しかし初等的な関数の中には、理論的な重要性が有理関数・代数関数・三角関数よりも劣るものの、グラフを描くことで関数的な関係の可能性をよりよく理解できるものが存在する。
-
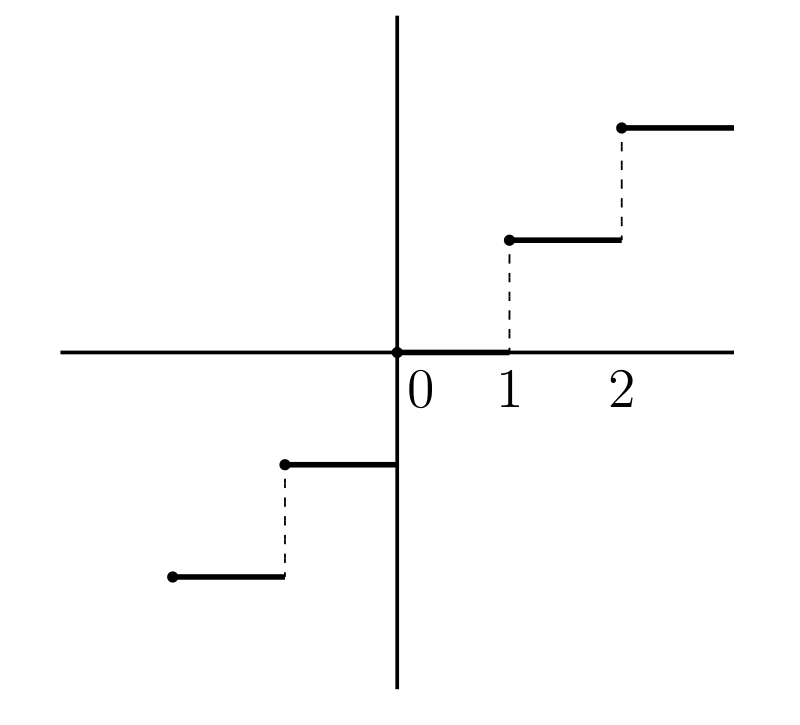
\(x\) を越えない最大の整数を \([x]\) で表すとする。\(y = [x]\) のグラフを 図 15a に示す。太線の左端の点はグラフに含まれるが、右端の点は含まれない。
-
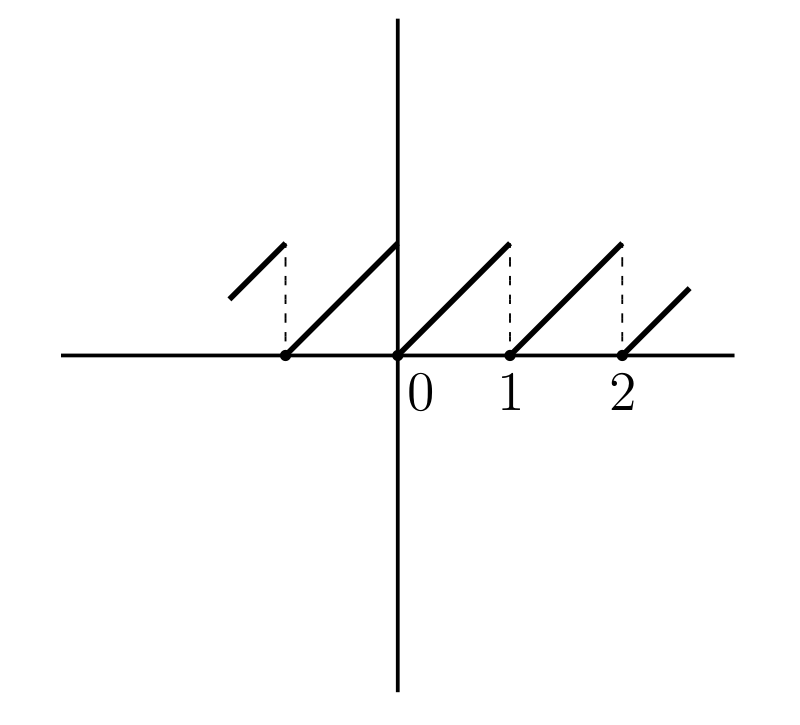
\(y = x - [x]\) (図 15b)
-
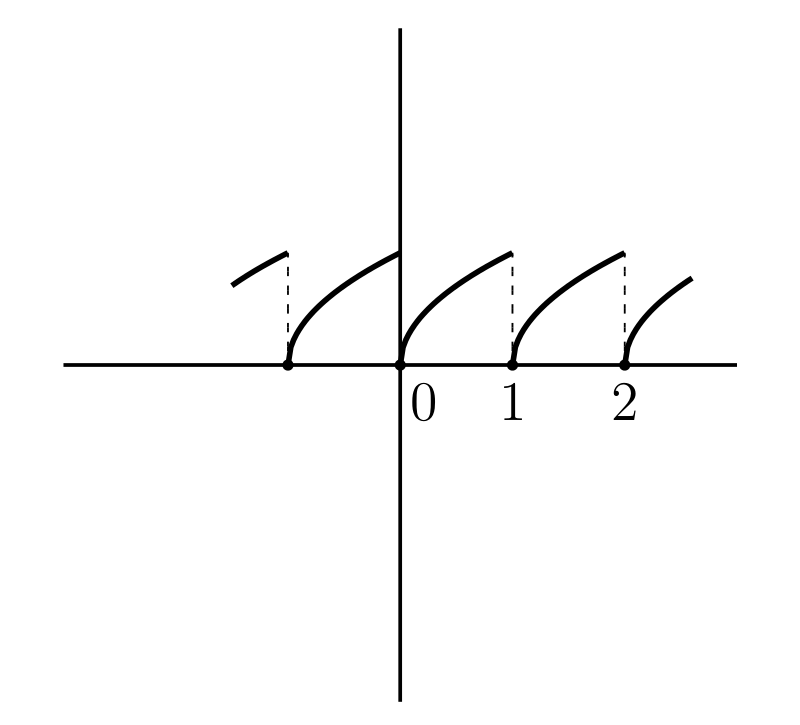
\(y = \sqrt{x - [x]}\) (図 15c)
-
\(y = [x] + \sqrt{x - [x]}\) (図 15d)
-
\(y = (x - [x])^{2},\ y = [x] + (x - [x])^{2}\)
-
\(y = [\sqrt{x}],\ y = [x^{2}],\ y = \sqrt{x} - [\sqrt{x}],\ y = x^{2} - [x^{2}],\ y = [1 - x^{2}]\)
-
\(y\) を \(\bm{x}\) の最大素因数と定義する (例 10.6)。このとき \(y\) は整数の \(x\) に対してのみ定義される。もし \[ x = 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9,\ 10,\ 11,\ 12,\ 13,\ \ldots, \] なら \[ y = 1,\ 2,\ 3,\ 2,\ 5,\ 3,\ 7,\ 2,\ 3,\ \hphantom{1} 5,\ 11,\ \hphantom{1} 3,\ 13,\ \ldots\hphantom{,} \] であり、グラフは孤立した点から構成される。
-
\(y\) を \(\bm{x}\) の分母とする (例 10.7)。すると \(y\) は有理数の \(x\) に対してしか定義されない。グラフ上の点は好きなだけ多くプロットできるが、最終的なグラフは通常の意味での曲線ではない。無理数 \(x\) に対応する点が存在しない。
\(N\) を正の整数として、点 \((N - 1, N)\) と \((N, N)\) を結ぶ直線を引く。この直線上にある点の個数が \(N\) と互いに素な \(N\) より小さい正の整数の数と等しいことを示せ。
-
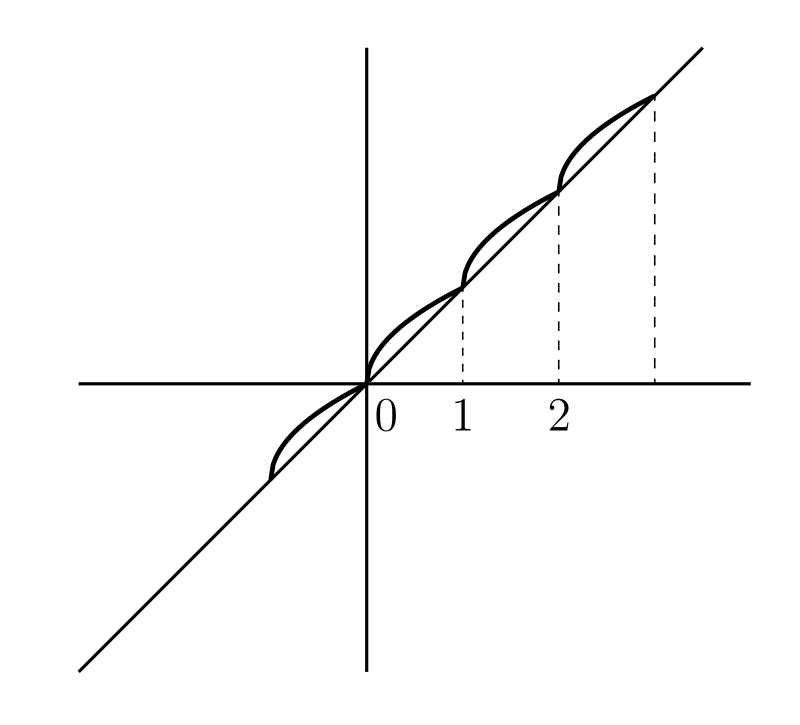
\(x\) が整数のとき \(y = 0\) で、\(x\) が整数でないとき \(y = x\) と定める。この関数のグラフは直線 \(y = x\) から \[ \ldots, \quad (-1, -1),\quad (0, 0),\quad (1, 1),\quad (2, 2),\quad \ldots \] という点を取り除き、\(x\) 軸上の \(\ldots,\ (-1, 0),\ (0, 0),\ (1, 0),\ \ldots\ \) という点を追加したものになる。
この関数は道理にかなっていないと読者は思うかもしれない。「整数でない \(x\) で \(y\) が \(x\) と等しいなら、整数でも \(y = x\) ではないか」と疑問に思うことだろう。この疑問に対する答えは「そうなるべき理由などない」である。実際のところこの \(y\) は関数の定義の本質をよく表していると言える: \(x\) と \(y\) の関係であって \(x\) が分かったときに \(y\) が分かるものであれば、それは関数となる。私たちには好きなようにこの関係を考える自由があり、それがどんなに人為的で荒唐無稽に見えても構わない。もちろんこの関数 \(y\) は、\(x\) が整数を含んだどんな値でも常に \(x\) に等しい関数とは全く異なる。
-
\(x\) が有理数のとき \(y = 1\) で、\(x\) が無理数のとき \(y = 0\) とする。この関数のグラフは \(y = 1\) と \(y = 0\) に並んだ二つの点列からなる。見た目では二つの連続な直線があるように見えるが、実際には抜けている点が両方の直線にそれぞれ無限個ある。
-
\(x\) が無理数のとき \(y = x\) で、\(x\) が有理数 \(p/q\) のとき \(y = \sqrt{(1 + p^{2})/(1 + q^{2})}\) とする。
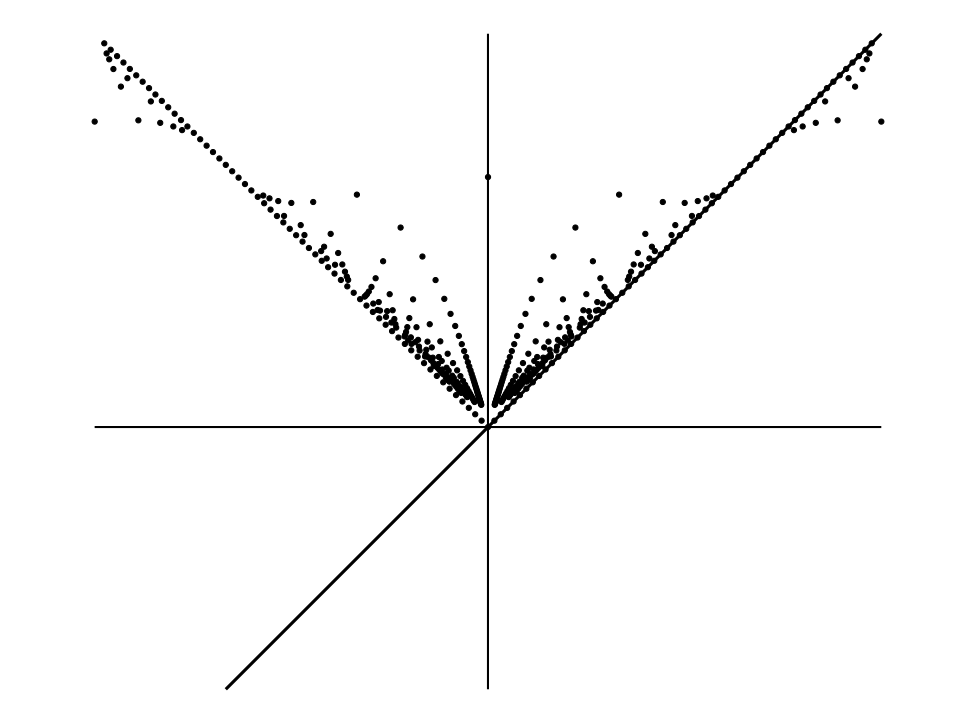 図 16
図 16この関数のグラフの無理数 \(x\) に対応する部分は本当は連続でないが、見た目では直線 \(y = x\) と区別が付かない。
有理数 \(x\) を考える。\(x\) が正なら、\(\sqrt{(1 + p^{2})/(1 + q^{2})}\) が \(p/q\) と等しくなるのは \(p = q\) すなわち \(x = 1\) のときだけである。つまり有理数 \(x\) に対応する \((1, 1)\) 以外の点は全て \(y = x\) から外れる。もし \(p \lt q\) なら \(\sqrt{(1 + p^{2})/(1 + q^{2})} \gt p/q\) が成り立ち、\(p \gt q\) なら \(\sqrt{(1 + p^{2})/(1 + q^{2})} \lt p/q\) が成り立つ。よって \(0 \lt x \lt 1\) なら点は \(y = x\) の上方にあり、\(1 \lt x\) なら下方にある。また \(p\) と \(q\) が大きいと \(\sqrt{(1 + p^{2})/(1 + q^{2})}\) はほぼ \(p/q\) に等しくなり、任意の有理数 \(x\) に対しては任意に大きい分母と分子を持った表現が存在するので、グラフの \(y = x\) の近くには大量の点が集まる。正の \(x\) に対するグラフの概形は直線とその周りに集まる孤立した点の集合からなり、点は直線に近づくほど濃くなる。
負の \(x\) に対応するグラフは、孤立した点を \(y\) 軸に関して対称にした点と不連続な \(y = x\) の残りの部分からなる。そのため \(y\) 軸より左側の点は \(y = x\) の周りではなく \(y = -x\) の周りに集まる。しかし \(y = -x\) はグラフに含まれない (図 16)。
§30 一変数方程式の図を使った解法
多くの方程式は次の形で表せる: \[ f(x) = \phi(x) \qquad \text{(1)} \] ここで \(f(x)\) と \(\phi(x)\) はグラフを簡単に描ける関数する。そして \[ y = f(x),\quad y = \phi(x) \] という二つの曲線が点 \(P\) で交わりその横座標が \(\xi\) なら、\(\xi\) は方程式 (1) の根となる。
-
二次方程式 \(\bm{ax^{2} + 2bx + c = 0}\): この方程式を視覚的に解く方法はいくつかある。例えばグラフ \[ y = ax + 2b,\quad y = -\frac{c}{x} \] に交点があれば、そこから根が分かる。あるいは次の曲線でも構わない: \[ y = x^{2},\quad y = -\frac{2bx + c}{a} \] しかし最も初等的な方法は、次の円を描く方法だろう: \[ a(x^{2} + y^{2}) + 2bx + c = 0 \] この円は中心 \((-b/a, 0)\) と半径 \(\{\sqrt{b^{2} - ac}\}/a\) を持つ。\(x\) 軸との交点の横座標が方程式の根となる。
-
前問のいずれかの方法を使って次の方程式を解け: \[ x^{2} + 2x - 3 = 0, \quad x^{2} - 7x + 4 = 0, \quad 3x^{2} + 2x - 2 = 0 \]
-
方程式 \(\bm{x^{m} + ax + b = 0}\): これは \(y = x^{m}\) と \(y = -ax - b\) を書けば解ける。\(x^{m} + ax + b = 0\) の根の個数に関する次の条件を確かめよ: \[ \begin{cases} m \text{ が偶数} \begin{cases} b \text{ が正: 二つまたは根なし} \\ b \text{ が負: 二つ} \\ \end{cases} \\ m \text{ が奇数} \begin{cases} a \text{ が正: 一つ} \\ a \text{ が負: 三つまたは一つ} \\ \end{cases} \\ \end{cases} \] 全ての場合について具体的な数値の例を示せ。
-
\(\tan x = ax + b\) が常に無限個の根を持つことを示せ。
-
次の方程式の根の個数を求めよ: \[ \sin x = x,\quad \sin x = \frac{1}{3} x, \quad \sin x = \frac{1}{8} x,\quad \sin x = \frac{1}{120} x \]
- \(a\) が小さい正の値 (例えば \(0.01\)) のとき、方程式 \[ x - a = \frac{1}{2}\pi\sin^{2} x \] が三つの根を持つことを示せ。\(a\) が小さい負の値のときも考え、\(a\) の変化に応じて根の個数がどのように変化するか説明せよ。
§31 二変数関数とその図示
§20 ではある関係で結ばれる二つの変数を考えた。同様に、ある関係で結ばれた三つの変数 (\(x, y, z\)) を考えることもできる。つまり \(x\) と \(y\) が両方分かれば \(z\) も分かるという関係である。このとき \(z\) を \(x\) と \(y\) の二変数関数と呼ぶ。\(x\) と \(y\) を独立変数 (independent variable) と呼び、\(z\) を 従属変数 (dependent variable) と呼ぶ。そして \(z\) の値が \(x\) と \(y\) の値から決定することを次の式で表す: \[ z = f(x, y) \] §20 の内容は必要な変更を加えればこの複雑なケースにも適用できる。
二変数関数を幾何学的に表す方法は一変数関数の場合と基本的に全く変わらない。三次元空間内に \(OX,\ OY,\ OZ\) という三つの軸が必要であり、それぞれが他の二つと直行する。点 \((a, b, c)\) はそれぞれ平面 \(YOZ,\ ZOX,\ XOY\) から \(OX,\ OY,\ OZ\) に平行に測った距離が \(a,\ b,\ c\) である点として定義される。もちろん符号を考慮し、\(OX,\ OY,\ OZ\) の方向を正とする。座標、軸、原点も同様に定義される。
さて \[ z = f(x, y) \] とする。\(x\) と \(y\) が変化すると、点 \((x, y, z)\) は空間内を動き回る。この点を全て集めたものを \((x, y, z)\) の軌跡 (locus) あるいは \(z = f(x, y)\) のグラフ (graph) と呼ぶ。\(z\) を定義するのに使う \((x,\ y)\) と \(z\) の間の関係が解析的な式として書けるなら、その式を軌跡の方程式と呼ぶ。例えば次の一般的な一次方程式 \[ Ax + By + Cz + D = 0 \] が平面を表すこと、および任意の平面の方程式がこの形であることは簡単に示せる。また方程式 \[ (x - \alpha)^{2} + (y - \beta)^{2} + (z - \gamma)^{2} = \rho^{2} \] および \[ x^{2} + y^{2} + z^{2} + 2Fx + 2Gy + 2Hz + C = 0 \] は球を表す (二つ目の式では \(F^{2} + G^{2} + H^{2} - C \gt 0\) とする)。ここでもこういった命題の証明は解析幾何学の教科書に譲る。
§32 平面内の曲線
ここまでは \[ y = f(x) \qquad \text{(1)} \] という表記で \(y\) の値が \(x\) から定まることを表現した。この表現が一番自然なのは、\(y\) が \(x\) の数式として明示的に書ける次のような場合である: \[ y = x^{2},\quad \sin x,\quad a\cos^{2}x + b\sin^{2}x \]
しかしこの形で表せない関係、あるいは表せたとしても複雑すぎて手に負えない関係を表す関数を扱わなければならない状況というのは非常に多い。例えば \(y^{5} - y - x = 0\) や \(x^{5} + y^{5} - ay = 0\) では、\(y\) を \(x\) の陽な代数関数として表現できない。あるいはもし \[ x^{2} + y^{2} + 2Gx + 2Fy+ C = 0 \] であれば、\(y\) は明示的に表現できる: \[ y = -F + \sqrt{F^{2} - x^{2} - 2Gx - C} \] しかしそうだとしても、\(x\) の関数 \(y\) と \(x\) との関係は最初の方程式を見た方が分かりやすい。
これら二種類の関数の関係が、二つの変数 \(\bm{x}\) と \(\bm{y}\) を持つ関数が \(\bm{0}\) に等しい関係として完全に表現できることに気が付くだろう。つまり次の方程式である: \[ f(x, y) = 0 \qquad \text{(2)} \]
これからは関数の関係を表現するのにこの方程式を標準形として使っていく。(1) は \(y - f(x)\) という特殊な形をした \(x\) の関数 \(y\) を表すので、この方程式は (1) を特殊ケースとして含む。この定義により「\(f(x, y) = 0\) を満たす点 \((x, y)\) の軌跡」「\(f(x, y) = 0\) で定義される関数 \(y\) のグラフ」「曲線 \(f(x, y) = 0\)」「軌跡 \(f(x, y) = 0\)」あるいは「曲線の方程式」や「軌跡の方程式」といった表現が可能になる。
曲線を表現するのに便利な方法がもう一つある。\(x\) と \(y\) がどちらも第三の変数 \(t\) の関数となる場合であり、このとき次のように書ける (\(t\) は補助的な変数であり、幾何学的な意味はない) : \[ x = f(t),\quad y = F(t) \qquad \text{(3)} \] \(t\) の値を定めると対応する \(x\) と \(y\) の値が決定し、二つの値が点 \((x, y)\) を定義する。異なる \(t\) の値に対応する点を全て集めれば、方程式 \(\bm{(3)}\) で定義される軌跡のグラフが手に入る。例えば \[ x = a\cos t,\quad y = a\sin t \] がその例である。\(t\) が \(0\) から \(2\pi\) まで動くとき \((x, y)\) が原点中心で半径 \(a\) の円を描くというのは容易に分かる。\(t\) がこの範囲を超えて動くと、\((x, y)\) は同じ円を何度も回る。この場合には二つの式を二乗して足せば \(x\) と \(y\) の直接的な関係を得られる: \(t\) が消えて \(x^{2} + y^{2} = a^{2}\) となる。
-
\(f\) と \(\phi\) を多項式とする。この二つの方程式が \(x\) と \(y\) に関する連立方程式として解けるとき、\(f(x, y) = 0,\ \phi(x, y) = 0\) という方程式で定義される二つの曲線の交点が求められる。通常この解は有限個の \((x, y)\) の組から構成される。つまり二つの方程式は有限個の孤立した点を表す。
-
曲線 \((x + y)^{2} = 1,\ xy = 1,\ x^{2} - y^{2} = 1\) が通る点を調べよ。
-
曲線 \(f(x, y) + \lambda\phi(x, y) = 0\) は \(f = 0\) と \(\phi = 0\) の交点を通る曲線を表す。
-
\(t\) が実数全てを動くとき、方程式 \[ \begin{aligned} (\alpha)\ \quad& x = at + b,\quad y = ct + d \\ (\beta)\ \quad& \frac{x}{a} = \frac{2t}{1 + t^{2}},\quad \frac{y}{a} = \frac{1 - t^{2}}{1 + t^{2}} \end{aligned} \] が表す軌跡は何か?
§33 空間内の軌跡
三つの次元を持つ空間では、本質的に異なる二つの軌跡が存在する。最も単純な例はそれぞれ直線と平面である。
直線上を移動する点は一次の自由度しか持たない。点の移動方向は固定され、その位置は固定点からの距離という一つの情報で完全に決定される。例えば直線として第一章で考えた基準直線 \(\Lambda\) を取れば、直線上の任意の点の位置は一つの座標 \(x\) で決定される。一方で平面上を動く点には二次の自由度があり、その位置の決定には二つの座標が必要となる。
一つの方程式 \[ z = f(x, y) \] が表す軌跡は二つ目のクラスに属する軌跡であり、曲面 (surface) と呼ばれる。この曲面は「曲面」という言葉から常識的に想像される特徴を持っていることもあれば持っていないこともある (簡単で単純なケースであれば普通は持っている)。
§31 での考察を一般化すれば、\(f(x, y, z)\) という三つの変数を持つ関数 (あるいは任意の数の変数を持つ関数) を定義できる。そして §32 で \(f(x, y) = 0\) を平面曲線の方程式の標準形として採用したように、これからは \[ f(x, y, z) = 0 \] を曲面の方程式の標準形として採用する。
\(z = f(x, y)\) あるいは \(f(x, y, z) = 0\) という形の方程式が二つあるなら、それは軌跡は第一のクラスに属する軌跡を定義する。例えば直線は \(Ax + By + Cz + D = 0\) という形をした二つの方程式で表せる。また空間内の円は球と平面の交わりであり、次の二つの方程式で表せる: \[ \begin{gathered} (x - \alpha)^{2} + (y - \beta)^{2} + (z - \gamma)^{2} = \rho^{2},\\ Ax + By + Cz + D = 0 \end{gathered} \]
-
\(f(x, y, z) = 0\) の形をした方程式が三つある場合、何を表すか?
-
三つの線形方程式は一般に単一の点を表す。例外はどんな場合か?
-
平面 \(XOY\) を曲面とみなしたとき、この曲面上の平面曲線 \(f(x, y) = 0\) の方程式は何か? [\(f(x, y) = 0,\ z = 0\)]
-
柱体: \(f(x, y) = 0\) という単一の方程式を三次元空間内の軌跡とみなしたとき、これは何を意味するか?
[この曲面上の全ての点は \(f(x, y) = 0\) を満たし、そのときの \(z\) の値は考慮されない。曲線 \(f(x, y) = 0,\ z = 0\) はこの曲面を平面 \(XOY\) で切ったものであり、この曲線上の全ての点から \(OZ\) 方向に直線を引くと考えている曲面となる。この曲面を柱体 (cylinder) と呼ぶ]
-
曲面の平面上における表現、等高線: 曲面を平面に描画するなど不可能に思える: 実際不可能である。しかし次の方法を使えば曲面の主な性質を理解できることが多い。考えている曲面の方程式を \(z = f(x, y)\) とする。
\(z\) に具体的な値 \(a\) を与えると、方程式 \(f(x, y) = a\) が手に入る。これは紙面上のとある平面曲線を定義しているとみなせるので、この曲線を描いて \((a)\) とする。この曲線 \((a)\) は曲面の \(z = a\) の部分を平面 \(XOY\) に射影したものである。全ての \(a\) の値についてこれを行う (もちろん実際には適当に選んだ \(a\) に対して行う) と、図 17 のような図が得られる。英国陸地測量部による等高線地図が思い浮かぶだろう: 実際そういった地図は同じような方法で作られる。地図の \(1000\) という等高線は、海面上 \(1000\) ft にある海面と平行な平面で陸地を切ったものを海面上の平面に射影したものである7。
 図 17
図 17 -
曲面 \(2z = 3xy\) を表す等高線を描け。
-
正円錐: 座標系の原点を円錐の頂点とし、\(z\) 軸を円錐の軸と同じ方向とする。さらに \(\alpha\) を円錐の母線と軸のなす角度とすれば、円錐の方程式は \(x^{2} + y^{2} - z^{2} \tan^{2} \alpha = 0\) である (曲面は頂点から \(z\) 軸の両方向に存在する)。
-
一般的な回転曲面: 問題 7 の正円錐を平面 \(ZOX\) で切ると、方程式 \(x^{2} = z^{2}\tan^{2}\alpha\) で表される二つの直線が手に入る。つまり曲線 \(y = 0,\ x^{2} = z^{2}\tan^{2}\alpha\) を \(z\) 軸の周りに回転させて得られる曲面の方程式は、二番目の方程式の \(x^{2}\) を \(x^{2} + y^{2}\) に変えると得られる。一般的に言って、曲線 \(y = 0,\ x = f(z)\) を \(z\) 軸の周りに回転させて得られる曲面の方程式が次の形をしていることを示せ: \[ \sqrt{x^{2} + y^{2}} = f(z) \]
-
一般化された錐: ある固定された点を通る直線によって構成される曲面を錐 (cone) と呼び、その点を錐の頂点 (vertex) と呼ぶ。問題 7 で考えた正円錐は錐の例である。頂点が \(O\) である錐の方程式が \(f(z/x, z/y) = 0\) という形をしていること、およびこの形をした方程式が錐を表すことを示せ。
-
線識面: 柱と錐は多数の直線から構成される曲面の一種である。このような曲面を線識面 (ruled surface) と呼ぶ。
二つの方程式 \[ x = az + b,\quad y = cz + d \qquad \text{(1)} \] は二つの平面の交わり、すなわち直線を表す。ここで \(a,\ b,\ c,\ d\) が固定されておらず、補助変数 \(t\) の関数だとする。すると \(t\) の値それぞれについて、方程式 (1) が直線を定める。\(t\) が変化すると直線が移動し、曲面が生成される。この曲面の方程式は二つの方程式 (1) から \(t\) を削除すれば得られる。例えば問題 7 の正円錐を生成する二つの方程式は \[ x = z\tan \alpha\cos t,\quad y = z\tan \alpha\sin t \] となる。ここで \(t\) は考えている直線と \(z\) 軸を通る平面と平面 \(XOZ\) のなす角度を表す。
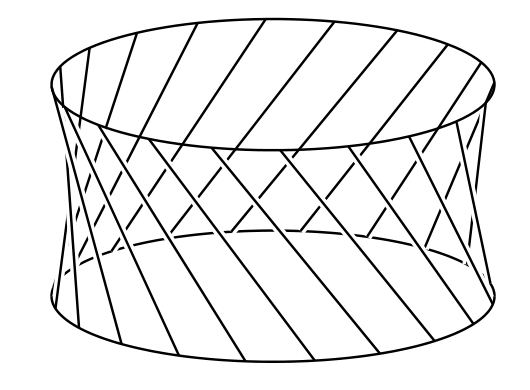
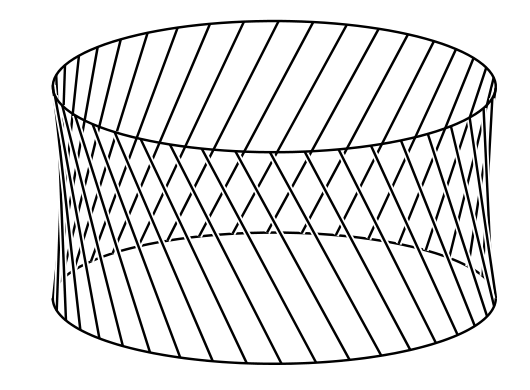
簡単な線識面の例をもう一つ示す。軸に平行な円柱の断面であって \(l\) だけ離れたものを二つ取る (図 18a)。このとき円柱の側面は \(PQ\) のような長さ \(l\) の平行な竿が集まったものとみなせる。このとき棒の両端は半径 \(a\) の円形の竿を二つ構成する。
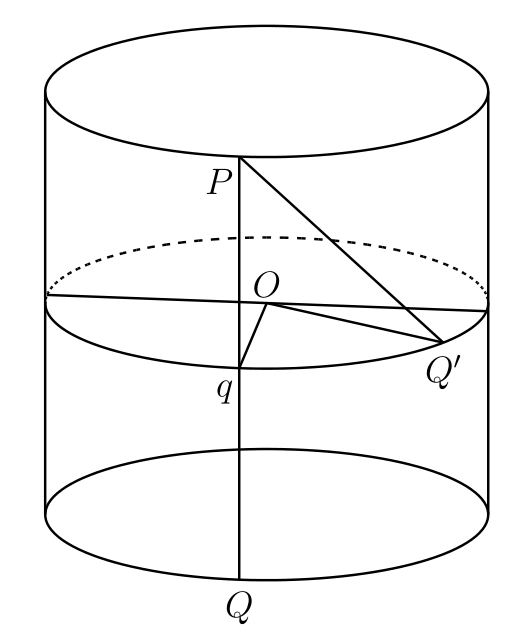 図 18a
図 18aここで新たな竿として、同じ半径を持った円形の竿を上下どちらかの円から \(h\) だけ離れた位置に追加する (図 18a では \(Pq = h\) となっている)。\(Q\) を \(PQ\) から切り離し、\(Q\) が第三の円に \(Q'\) で触れるように傾ける。図中の \(\angle qQQ' = \alpha\) は次の式を満たす: \[ l^{2} - h^{2} = q{Q'}^{2} = \left (2a\sin\frac{1}{2} \alpha\right)^{2} \] 正円錐を構成する竿の全てに同じ操作を行うと、図 18b のような線識面が手に入る。この線識面は直線だけから構成されているにもかかわらず、いたるところが曲がっている。形としてはテーブルナプキンを丸めたものに近い (図 18c)。
第二章に関するその他の例
-
\(y = f(x) = \dfrac{ax + b}{cx - a}\) なら \(x = f(y)\) だと示せ。
-
全ての \(x\) に対して \(f(x) = f(-x)\) なら、\(f(x)\) を偶関数 (even function) と呼ぶ。全ての \(x\) について \(f(x) = -f(x)\) なら、\(f(x)\) を奇関数 (odd function) と呼ぶ。全ての \(x\) に対して定義された任意の関数は \(x\) の奇関数と偶関数の和であることを示せ。
[等式 \(f(x) = \frac{1}{2}\{f(x) + f(-x)\} + \frac{1}{2}\{f(x) - f(-x)\}\) を使う]
-
次の関数のグラフを描け: \[ 3\sin x + 4\cos x,\quad \sin\left(\frac{\pi}{\sqrt{2}} \sin x\right) \]
(Math. Trip. 1896.)
-
次の関数のグラフを描け: \[ \sin x(a\cos^{2} x + b\sin^{2} x), \quad \frac{\sin x}{x}(a\cos^{2} x + b\sin^{2} x), \quad \left(\frac{\sin x}{x}\right)^{2} \]
-
関数 \(x\left[\dfrac{1}{x}\right],\ \ \dfrac{[x]}{x}\) のグラフを描け。
-
次の関数のグラフを描け: \[ \begin{aligned} & \,\text{(i)}\, \arccos(2x^{2} - 1) - 2 \arccos{x} \\ & \text{(ii)} \arctan \frac{a + x}{1 - ax} - \arctan{a} - \arctan{x} \end{aligned} \] \(\arccos a,\ \arctan a\) は任意の値 \(a\) に対してコサインとタンジェントが \(a\) である値の中で一番小さい正の値を返すとする。
-
\(f(x)\) と \(\phi(x)\) のグラフから \(f\{\phi(x)\}\) のグラフを作る次の方法が正しいことを確かめよ: \(OX\) 上に \(OA = x\) を取り、\(A\) を通って \(OY\) に平行な直線が \(y = \phi(x)\) と交わる点を \(B\) とし、\(B\) を通って \(OX\) に平行な直線が \(y = x\) と交わる点を \(C\) とし、\(C\) を通って \(OY\) に平行な直線が \(y = f(x)\) と交わる点を \(D\) とし、\(D\) を通って \(OX\) に平行な直線が \(AB\) と交わる点を \(P\) とする。すると \(P\) が求めるグラフ上の点となる。
-
\(x^{3} + px + q = 0\) の根が、放物線 \(y = x^{2}\) と次の円との (原点でない) 交点の横座標であることを示せ: \[ x^{2} + y^{2} + (p - 1)y + qx = 0 \]
-
\(x^{4} + nx^{3} + px^{2} + qx + r = 0\) の根は放物線 \(x^{2} = y - \frac{1}{2}nx\) と次の円の交点の横座標である: \[ x^{2} + y^{2} + (\frac{1}{8}n^{2} - \frac{1}{2}pn + \frac{1}{2}n + q)x + (p - 1 - \frac{1}{4}n^{2})y + r = 0 \]
-
次の方程式の解について、視覚的に議論せよ: \[ x^{m} + ax^{2} + bx + c = 0 \] 議論には曲線 \(y = x^{m}\) と \(y = -ax^{2} - bx - c\) を利用せよ。また可能な根の個数について表にまとめよ。
-
方程式 \(\sec\theta + \cosec\theta = 2\sqrt{2}\) を解け。方程式 \(\sec\theta + \cosec\theta = c\) が \(c^{2} \lt 8\) なら \(0\) と \(2\pi\) の間に二つの根を持ち、\(c^{2} \gt 8\) なら同じ区間に四つの根を持つことを示せ。
-
\(n\) を正の整数として、方程式 \[ 2x = (2n + 1)\pi(1 - \cos x) \] がちょうど \(2n + 3\) 個の根を持つことを示せ。ここから根の局所性が分かる。
(Math. Trip. 1896.)
-
方程式 \(\dfrac{2}{3}x\sin x = 1\) が \(-\pi\) と \(\pi\) の間に四つの根を持つことを示せ。
-
次の方程式の根の個数と値を議論せよ:
- \(\cot x + x - \frac{3}{2}\pi = 0\)
- \(x^{2} + \sin^{2} x = 1\)
- \(\tan x = 2x/(1 + x^{2})\)
- \(\sin x - x + \frac{1}{6}x^{3} = 0\)
- \((1 - \cos x)\tan\alpha - x + \sin x = 0\)
-
\(x = a,\ b,\ c\) のときの値がそれぞれ \(\alpha,\ \beta,\ \gamma\) であるような二次方程式は次の式で表せる: \[ \alpha\frac{(x - b)(x - c)}{(a - b)(a - c)} + \beta \frac{(x - c)(x - a)}{(b - c)(b - a)} + \gamma\frac{(x - a)(x - b)}{(c - a)(c - b)} \] 同様に \(x = a_{1},\ a_{2},\ \ldots,\ a_{n}\) のときの値がそれぞれ \(\alpha_{1},\ \alpha_{2},\ \ldots,\ \alpha_{n}\) となるような \(n-1\) 次方程式を示せ。
-
\(x\) の二次多項式であって \(x\) が \(0,\ 1,\ 2\) のときの値がそれぞれ \(1/c,\ 1/(c + 1),\ 1/(c + 2)\) となるようなものを求めよ。\(x = c + 2\) のときの値が \(1/(c + 1)\) であると示せ。
(Math. Trip. 1911.)
-
\(x\) が \(y\) の有理関数でかつ \(y\) が \(x\) の有理関数なら \(Axy + Bx + Cy + D = 0\) だと示せ。
-
\(y\) が \(x\) の代数関数なら \(x\) は \(y\) の代数関数だと示せ。
-
\(x\) が \(0\) と \(1\) の間にあるとき、等式 \[ \cos\frac{1}{2}\pi x = 1 - \frac{x^{2}}{x + (x - 1)\sqrt{\frac{2 - x}{3}}} \] が近似的に正しいことを示せ。 [\(x = 0,\ \frac{1}{6},\ \frac{1}{3},\ \tfrac{1}{2},\ \frac{2}{3},\ \frac{5}{6},\ 1\) として表にまとめよ。式が正確に正しくなる \(x\) はどれか?]
-
次の関数のグラフはどんな形をしているか? \[ z = [x] + [y],\quad z = x + y - [x] - [y] \]
-
関数 \(z = \sin x + \sin y,\ z = \sin x\sin y,\ z = \sin xy,\ z = \sin(x^{2} + y^{2})\) のグラフはどんな形をしているか?
-
無理数の幾何学的構成: 単位長から始めて \(\sqrt{2}\) と等しい長さを幾何学的に構成する方法を第一章でいくつか示した。また二次方程式 \(ax^{2} + 2bx + c = 0\) の根の構成方法も示したが、そのときには有理数の係数 \(a,\ b,\ c\) の比と等しい長さの線分を作れることを利用した。こういった構成はどれも定規とコンパスだけを使っており、ユークリッドの構成 (Euclidean construction) と呼ばれる。
二乗根の組み合わせで定義される無理数であればどんなに複雑なものであっても、それと同じ長さをユークリッドの構成で作れる。例えば \[ \sqrt[4]{\sqrt{\frac{17 + 3\sqrt{11}}{17 - 3\sqrt{11}}} - \sqrt{\frac{17 - 3\sqrt{11}}{17 + 3\sqrt{11}}}} \] がその例である。この式には四乗根が出てくるが、もちろんこれは二乗根の二乗根と等しい。構成は \(1\) と \(11\) の幾何学平均 \(\sqrt{11}\) から始まり、それから \(17 + 3\sqrt{11}\) と \(17 - 3\sqrt{11}\) などが続く。あるいはこの二つの不尽根数の組を \(x^{2} - 34x + 190 = 0\) の根として直接得ることもできる。
逆に、ユークリッドの構成を使って構成できる無理数はこの種類に限られることが証明できる。有理数については単位長から任意の長さを構成できるので、有理数 \(A,\ B,\ C\) に対する直線 \(Ax + By + C = 0\)、および有理数 \(\alpha,\ \beta,\ \rho\) に対する円 \[ (x - \alpha)^{2} + (y - \beta)^{2} = \rho ^{2} \] を構成できる。円の方程式は \(x^{2} + y^{2} + 2gx + 2fy + c = 0\) でもよく、このとき \(\alpha,\ \beta,\ \rho\) が有理数なら \(g,\ f,\ c\) も有理数となる。
ユークリッドの構成において図に新たな点が加わるとき、その点は二点、二円、または円と直線の交点として決定される。しかし係数が有理数という仮定の下では、次の二つの方程式 \[ Ax + By + C = 0,\quad x^{2} + y^{2} + 2gx + 2fy + c = 0 \] の組から得られる解 \(x\) と \(y\) は \(m + n\sqrt{p}\) の形をした値だけである (\(m,\ n,\ p\) は有理数)。実際二つ目の方程式の \(x\) に \(y\) の式を代入すると二次方程式が手に入るので、有理係数の直線と円から得られる点の座標は有理数と二次の不尽根数だけと分かる。二点間の距離 \(\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}\) についても同様のことが言える。
このように構成される無理数の長さを使うと、係数に二次の不尽根数を含んだ直線と円を構成できる。しかしそういった直線と円を使って構成できるどんな長さも、複雑にはなるにせよ二次根号だけを使って表すことができる。そしてこの事実は構成が何度反復されても揺るがない。よってユークリッドの構成は二次の根号だけを使った不尽根数からなる数を全て構成し、それ以外は構成しない。
立方体倍積問題と呼ばれる古くからある有名な問題がある。ユークリッドの構成を使って \(\sqrt[3]{2}\) の長さを作れるか、という問題である。\(\sqrt[3]{2}\) は有理数と二乗根を使って表せないことが示せるので、この問題は不可能であると結論できる。詳しくはホブソン著 Squaring the Circle, pp. 47 et seq. を参照してほしい。\(\sqrt[3]{2}\) が有理係数二次方程式 \(ax^{2} + 2bx + c = 0\) の根にならないことは第一章に関するその他の例 24 で示した。
-
円積問題の近似解: 半径 \(R\) の円の中心を \(O\) とする。円周上の点 \(A\) を通る接線上に \(AP = \frac{11}{5}R\) および \(AQ = \frac{13}{5}R\) となるように \(P\) と \(Q\) を同じ方向に取る。\(AO\) 上に \(AN = OP\) となる \(N\) を取り、\(N\) を通って \(OQ\) に平行な直線が \(AP\) と交わる点を \(M\) とする。このとき次の式を示せ: \[ \frac{AM}{R} = \frac{13}{25}\sqrt{146} \] さらに \(AM\) を円周の近似値とみなせば、小数以下第五位まで正しい \(\pi\) の値が得られていることを示せ。\(R\) を地球の半径とすると、\(AM\) と円周の間の誤差は \(11\) ヤード以下となる。
-
単位長から定規だけで構成できる長さは有理数だけだと示せ。
-
\(\sqrt[3]{2}\) の構成: 放物線 \(y^{2} = 4x\) の頂点を \(O\)、焦点 を \(S\) とする。この放物線ともう一つの放物線 \(x^{2} = 2y\) の \(O\) でない交点を \(P\) とし、\(OP\) が一つ目の放物線の通径 (latus rectum) と交わる点を \(Q\) としたとき、\(SQ = \sqrt[3]{2}\) を示せ。
-
直径が単位長の円を考え、直径 \(OA\) と \(A\) を通る接線を取る。\(O\) を通る弦を取り、円との交点を \(B\)、接線との交点を \(C\) とする。さらにこの直線上に \(OM = BC\) となるように \(M\) を取る。\(O\) を原点、\(OA\) を \(x\) 軸としたとき、\(M\) の軌跡が次の直線であることを示せ: \[ (x^{2} + y^{2})x - y^{2} = 0 \] (この曲線はディオクレスのシッソイド (Cissoid of Diocles) と呼ばれる)。曲線を描き、\(y\) 軸上に \(OD = 2\) となる点 \(D\) を取る。\(AD\) が曲線と交わる点を \(P\) とし、\(A\) を通る円の接線と \(OP\) の交点を \(Q\) とする。このとき \(AQ = \sqrt[3]{2}\) を示せ。
-
この教育的な例は H・S・カースロー著 Introduction to the Calculus から取った。[return]
-
\(B = 0\) だと方程式から \(y\) が消える。このとき \(y\) は \(x = -C/A\) という単一の値に対してのみ定義される関数とみなされる。この \(x\) に対して \(y\) は全ての値を取る。[return]
-
極座標は \(r\) が正でも負でもあり得るように定義されることもある。こうすると二つの座標 —例えば \((1, 0)\) と \((-1, \pi)\)— が同じ点を表す。二つの座標系の違いは \(l \gt 0\) と \(e \gt 1\) を使った方程式 \(l/r = 1 - e\cos\theta\) を考えると明らかになる。私たちの定義では \(r\) は正なので \(\cos\theta \lt 1/e\) が成り立ち、方程式は双曲線の一方の枝だけを表す。一方で負の \(r\) を許す座標系なら \(-l/r = 1 - e\cos\theta\) も含まれるので、双曲線全体が表される。[return]
-
\(y\) 軸方向の目盛りを \(x\) 軸方向の目盛りより小さく描いた方がよい。そうしないと図がとてつもない大きさになる[return]
-
初等三角法における三角関数の定義では、円に含まれる任意の扇形に対して面積 (area) と呼ばれる有限の値が存在することが仮定される。この仮定の正当化は第七章で見る。[return]
-
地球の曲率は無視している。[return]