§156 定積分と面積
第六章の §145 では、\(PQ\) を \(x\) の連続関数 \(f(x)\) のグラフとしたとき 図 47 における領域 \(PpqQ\) に面積と呼ばれる値が定義されることを仮定して話を進めた。\(Op\) と \(Oq\) を \(a\) と \(x\) して \(x\) を変化させると、明らかにこの面積は \(x\) の関数となる。この関数を \(F(x)\) と表す。
§145 ではこの仮定の下で \(F'(x) = f(x)\) を示し、この結果を使えば特定の曲線の面積を計算できることを示した。しかし面積 \(F(x)\) なる値が存在するという最初の仮定はまだ正当化されていない。
長方形には面積が存在し、その値がニ辺の長さの積として得られることを私たちは知っている。またユークリッドによって示された三角形や平行四辺形あるいは多角形の性質を使えば、そういった図形の面積の意味を定められる。しかし現在の私たちは、曲線で囲まれた図形の面積の直接的な定義を知らない。これから \(F(x)\) に定義を与え、面積の存在を証明する方法を示す1。

\(f(x)\) が区間 \([a, b]\) で連続として、\([a, b]\) を \(x_{0},\ x_{1},\ x_{2},\ \ldots,\ x_{n}\) という分割点を使って複数の小区間に分割する。ここで \[ a = x_{0} \lt x_{1} \lt \cdots \lt x_{n-1} \lt x_{n} = b \] とする。さらに区間 \([x_{\nu}, x_{\nu+1}]\) (およびその長さ) を \(\delta_{\nu}\) と表記し、\(m_{\nu}\) で \(\delta_{\nu}\) における \(f(x)\) の下限 (§102) を表す。そして \[ s = m_{0}\delta_{0} + m_{1}\delta_{1} + \cdots + m_{n}\delta_{n} = \sum m_{\nu}\delta_{\nu} \] と定める。
\(M\) を \([a, b]\) における \(f(x)\) の上限とすれば、明らかに \(s \leq M(b - a)\) が成り立つ。よって §80 の言葉を使えば、\(s\) の取る値の集まりは上に有界となる。この集まりの上限を \(j\) とすれば、\(j\) より大きい \(s\) の値は存在せず、\(j\) より小さい任意の数より大きい \(s\) の値が存在する。
同様に \(\delta_{\nu}\) における \(f(x)\) の上限を \(M_{\nu}\) として、和 \[ S = \sum M_{\nu}\delta_{\nu} \] を定義する。
\([a, b]\) における \(f(x)\) の下限を \(m\) とすれば \(S \geq m(b - a)\) が成り立つ。よって \(S\) が取る値は下に有界であり、下限 \(J\) を持つ。\(J\) より小さい \(S\) の値は存在せず、\(J\) より大きい任意の数より小さい \(S\) が存在する。
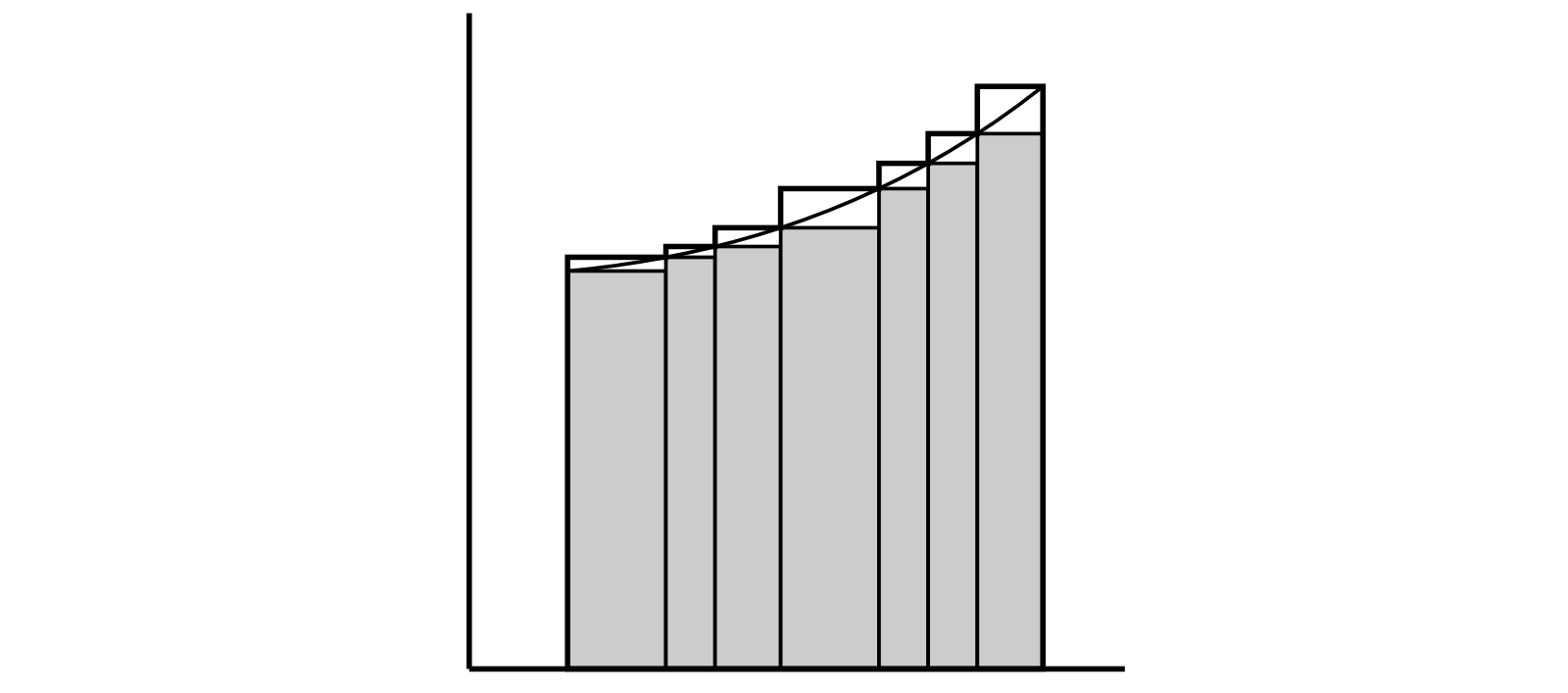
和 \(s\) と \(S\) の意味を理解するために、\(f(x)\) が \(x = a\) から \(x = b\) まで単調に増加するなら \(m_{\nu} = f(x_{\nu})\) かつ \(M_{\nu} = f(x_{\nu + 1})\) が成り立つことを納得しておくとよい。このとき 図 48 で灰色になっている長方形の面積の和が \(s\) で、太線で囲まれた領域の面積が \(S\) となる。一般に \(s\) と \(S\) は長方形からなる領域であり、面積を定義しようとしている曲線で囲まれた領域は \(s\) を含み、\(S\) に含まれる。
任意の和 \(\bm{s}\) が任意の和 \(\bm{S}\) よりも小さくなることを示す。ある分割に対応する和を \(s,\ S\) として、もう一つの適当な分割に対応する和を \(s',\ S'\) とする。\(s \leq S'\) と \(s' \leq S\) を示す必要がある。
\(s,\ S\) と \(s',\ S'\) に対応する二つの分割の分割点を全て取ることで、新しい分割を定義できる。この分割に対応する和を \(\mathbf{s},\ \mathbf{S}\) とすれば、明らかに \[ \mathbf{s} \geq s,\quad \mathbf{s} \geq s',\quad \mathbf{S} \leq S,\quad \mathbf{S} \leq S' \qquad \text{(1)} \] が成り立つ。例えば \(\mathbf{s}\) と \(s\) の違いを考えると、\(s\) に含まれる少なくとも一つの区間 \(\delta_{\mu}\) は、\(\mathbf{s}\) においていくつかの小区間 \[ \delta_{\nu, 1},\ \delta_{\nu, 2},\ \ldots,\ \delta_{\nu, p} \] に分割される。そのため \(s\) の \(m_{\nu}\delta_{\nu}\) という項は \(\mathbf{s}\) では \[ m_{\nu, 1}\delta_{\nu, 1} + m_{\nu, 2}\delta_{\nu, 2} + \cdots + m_{\nu, p}\delta_{\nu, p} \] という和になる。ここで \(m_{\nu, 1},\ m_{\nu, 2},\ \ldots\) は \(\delta_{\nu, 1},\ \delta_{\nu, 2},\ \ldots\) における \(f(x)\) の下限を表す。明らかに \(m_{\nu, 1} \geq m_{\nu},\ m_{\nu, 2} \geq m_{\nu},\ \ldots\) なので、この和は \(m_{\nu}\delta_{\nu}\) 以上である。よって \(\mathbf{s} \geq s\) が分かる。\(\text{(1)}\) の他の不等式も同様に示せる。さらに \(\mathbf{s} \leq \mathbf{S}\) だから、 \[ s \leq \mathbf{s} \leq \mathbf{S} \leq S' \] が分かる。これが証明すべきことだった。
また \(j \leq J\) も分かる。\(j\) に好きなだけ近い \(s\) と \(J\) に好きなだけ近い \(S\) を見つけられる2ので、\(j \gt J\) が成り立つなら \(s \gt S\) となる \(s\) と \(S\) が存在してしまう。
ここまでは \(f(x)\) が連続という事実を使ってこなかった。続いて \(j = J\) を示すときにこの事実を使う。区間 \(\delta_{\nu}\) の長さが \(0\) になるように分割点 \(x_{\nu}\) を増やしていくと、和 \(s\) および \(S\) が極限 \(J\) に向かうことも示す。より正確に言うと、任意の正の実数 \(\varepsilon\) に対して、全ての \(\nu\) で \(\delta_{\nu} \lt \delta\) なら \[ 0 \leq J - s \lt \varepsilon,\quad 0 \leq S - J \lt \varepsilon \] となる \(\delta\) が見つけられることを示す。
§106 の定理 2 から、ある \(\delta\) が存在して、全ての \(\delta_{\nu}\) が \(\delta\) より小さいなら \[ M_{\nu} - m_{\nu} \lt \frac{\varepsilon}{b - a} \] が成り立つ。よって \[ S - s = \sum (M_{\nu} - m_{\nu})\, \delta_{\nu} \lt \varepsilon \] となる。一方 \[ S - s = (S - J) + (J - j) + (j - s) \] であり、右辺の三項は全て正なので、この三項は全て \(\varepsilon\) より小さい。\(J - j\) は定数だから、\(0\) でなければならない。すなわち \(j = J\) かつ \(0 \leq j - s \lt \varepsilon,\ 0 \leq S - J \lt \varepsilon\) であり、示すべき関係が証明された。
領域 \(PpqQ\) の面積を \(\bm{s}\) と \(\bm{S}\) の共通の極限 \(\bm{J}\) として定義する。この定義にはより一般的で簡単な形が存在する。次の和を考える: \[ \sigma = \sum f_{\nu}\delta_{\nu} \] ここで \(f_{\nu}\) は \(\delta_{\nu}\) の適当な点における \(f(x)\) の値とする。\(\sigma\) は \(s\) と \(S\) の間にあるので、\(\delta_{\nu}\) が \(0\) に向かうとき極限 \(J\) に向かう。よって領域 \(PpqQ\) の面積を \(\sigma\) の極限として定義できる。