§3 無理数 (その 1)
分母が \(1,2,3, \ldots\) である有理数に対応する数直線上の点全てに印を付けるところを想像すれば、有理点を使って数直線上に好きなだけ細かく印を付けられることを納得できるだろう。これを正確に表現すれば「\(\Lambda\) 上に任意の線分 \(BC\) を取ると、\(BC\) 上に好きなだけ多くの有理点を見つけられる」となる。
例えば \(BC\) が線分 \(A_{1}A_{2}\) の中に含まれるとする。正の整数 \(k\) を \[ k · BC \gt 1 \qquad \text{(1)} \] が成り立つように選び1、それから \(A_{1}A_{2}\) を \(k\) 分割すれば、その分割点のうち少なくとも一つは \(BC\) 内部にあり、さらにそれは \(B\) でも \(C\) でもない (これを \(P\) とする)。もしこうならないなら \(A_{1}A_{2}\) を \(k\) 分割した部分を \(BC\) が完全に含むが、これは仮定 \(\text(1)\) と矛盾する。よって少なくとも一つの有理点 \(P\) が \(B\) と \(C\) の間にある。しかしもしそうならば \(B\) と \(P\) の間にも有理点 \(Q\) があり、以下同様に議論できる。つまり上述の通り、有理点を好きなだけ多く見つけられる。この事実を「\(BC\) は無限に多くの (infinitely many) 有理点を含む」と表現する。
「\(BC\) は無限に多くの有理点を含む」や「\(BC\) 上の有理数の個数は無限大である」あるいは「正の整数は無限大である」といった表現に含まれる「無限に多くの (infinitely many)」や「無限大 (an infinity of)」といった言葉の意味については 第四章で詳しく触れる。「正の整数は無限大である」という主張は「任意の正の整数 \(n\) が与えられたとき、\(n\) が \(100,000\) でも \(100,000,000\) でも、あるいはどれだけ大きかろうと、常に \(n\) より大きい整数を見つけられる」を意味する。「好きなだけ多くの正の整数を見つけられる」と言っても意味は変わらない。
この節の第二段落で証明した主張と本質的に同値な次の命題の正しさを、読者は容易に納得できるだろう: 「任意の有理数 \(r\) と正の整数 \(n\) が与えられたとき、\(r\) から両方向に \(1/n\) だけ離れた値と \(r\) の間に有理数を見つけられる」 これを異なる方法で表現すると「\(r\) から両方向に好きなだけ小さい幅だけ離れた値と \(r\) の間に有理数が存在する」となる。また任意の二つの有理数 \(r, s\) について、任意の二項が好きなだけ小さい幅だけ離れた有理数の列を使って二つの値をつなげられる。つまり先立って与えられた任意の正の整数 \(n\) に対して、隣り合う有理数の幅が \(1/n\) より小さい列が作れる。
こういった考察から、数直線上の有理点だけを考えれば数直線の本質的な概念が得られると思うかもしれない。数直線が有理数のみから構成されるとみなしてその他は (もしあったとしても) 無視するのなら、もちろんこれは正しい。こうして得られる概念は直線に関する常識的な特徴の多くを持ち、直線と同じような見た目をして同じように振る舞う。
しかし考察を少し進めると、この考え方が持つ深刻な問題が明らかになる。
これからしばらくは常識的な目でこの問題を観察し、初等幾何学が扱う性質を満たす直線が当然持つはずの特徴について考える。
直線は、端点の間にある全ての点およびそれらを結んだ線分から構成されるはずである。線分はどれも長さを持ち、長さは基準あるいは単位長を使って数値として表せる量であり、加算と乗算に関する通常の代数法則を使って組み合わせられる必要がある。つまり二つの線分が与えられたときに、長さがその和または積の直線を構築できなければならない。具体的に言えば同じ直線上にある線分 \(PQ,\ QR\) の長さがそれぞれ \(a,\ b\) なら、\(PR\) の長さは \(a + b\) となる。さらに同じ直線上にある線分 \(OP,\ OQ\) の長さがそれぞれ \(1,\ a\) で、他の直線上にある線分 \(OR\) の長さが \(b\) なら、ユークリッドの構成 (Euc. vi. 12) を使って \(OP,\ OQ,\ OR\) に対する第四比例項 (fourth proportional) として長さ \(ab\) の線分 \(OS\) を構成できる必要がある。つまり \(1,\ a,\ b\) に対する代数的な第四比例項である。このように定義される和と積が次の「代数法則」に従わなければならないのは言うまでもない: \[ \begin{gathered} a + b = b + a,\quad a + (b + c) = (a + b) + c,\\ ab = ba,\quad a(bc) = (ab)c,\quad a(b + c) = ab + ac \end{gathered} \] さらに今考えている直線の長さは、等式だけではなく不等式に関する数々の自明な法則も満たす必要がある: 例えば「もし \(A,\ B,\ C\) が直線 \(\Lambda\) 上に左から右にある点なら \(AB \lt AC\)」といった法則が成り立たなくてはならない。また任意の直線上の線分と同じ長さの線分を基準となる直線 \(\Lambda\) 上に取れる必要がある。こういった直線の性質は初等幾何学の公理から要請される。
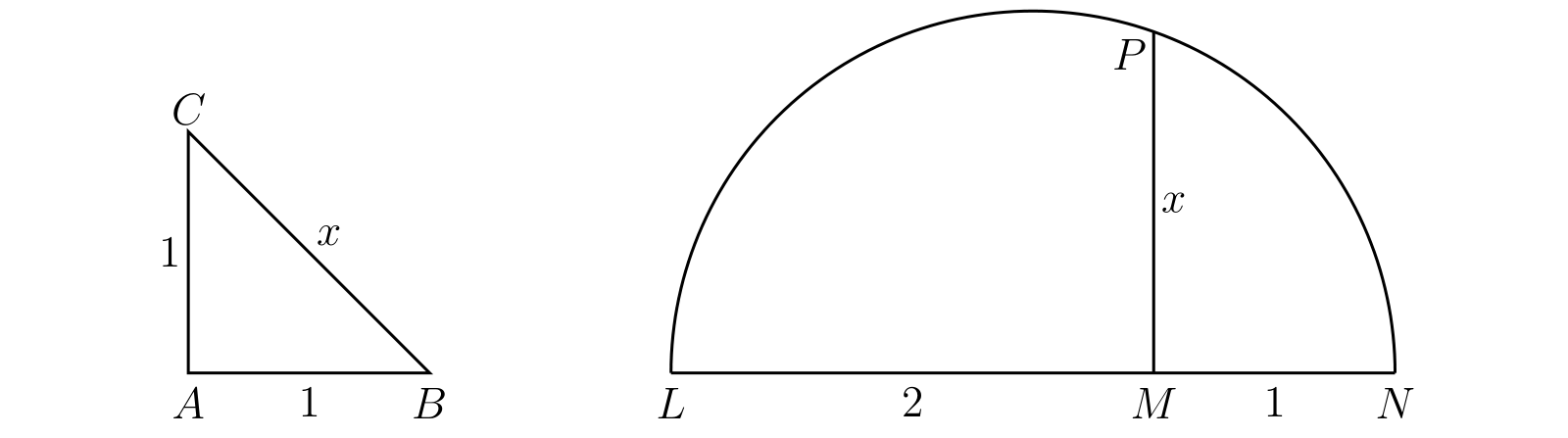
ここまでくれば、有理数に対応する点列から構成される直線の概念がこれまで述べてきた要件の全てを満たせないことが簡単に示せる。長さ \(x\) が \(x^{2} = 2\) を満たす線分を構成する幾何学的操作が存在する。例えば \(AB = AC = 1\) である垂直二等辺三角形 \(ABC\) では \(BC = x\) とすれば \(x^{2} = 2\) となる。あるいはユークリッドの構成 (Euc. vi. 13) を使って \(1\) と \(2\) の比例中項 (mean proportional) として 図 2 のように長さ \(x\) を得ることもできる。したがって先述の要件から、この数 \(x\) で表される長さ、そして次の等式を満たす \(\Lambda\) 上の点 \(P\) が存在しなければならない: \[ A_{0}P = x,\quad x^{2} = 2 \] しかし二乗すると \(\bm{2}\) になる有理数は存在しないことは容易に分かる。実を言えば、二乗すると正の既約分数 \(m/n\) になる有理数は、\(m\) と \(n\) が両方とも完全平方数でない限り存在しない。
証明は次の通り。それが可能だったとして \[ \frac{p^{2}}{q^{2}} = \frac{m}{n} \] と仮定する。ここで \(p\) と \(q\) は共通因数を持たず、\(m\) と \(n\) も共通因数を持たないとする。すると \(q^{2}\) の任意の約数は \(np^{2}\) を割り切らなければならない。\(p\) と \(q\) に共通因数がないので、\(q^{2}\) の任意の約数は \(n\) を割り切らなければならない。よって整数 \(\lambda\) を使って \(n = \lambda q^{2}\) と表せる。しかしこのとき \(m = \lambda p^{2}\) であり、\(m\) と \(n\) に共通因数がないので、\(\lambda\) は \(1\) である必要がある。したがって証明したい式 \(m = p^{2},\ n = q^{2}\) が得られる。ここに具体的な数字 \(n = 1\) を当てはめると、有理数の二乗が整数になるのはその有理数が整数である場合に限られると分かる。
つまり私たちが考えている要件には、前に構築した有理点だけではなく、\(A_{0}P = x\) かつ \(x^{2} = 2\) となる点 \(P\) と数 \(x\) が必要になる。そして初等代数で習った通り、この数 \(x\) を \(x = \sqrt{2}\) と表記する。
二乗が \(2\) に等しい有理数が存在しないことの興味深い別証明を示す:
二乗が \(2\) になる有理数があるとして、\(p/q\) が既約で正の分数であり、\((p/q)^{2} = 2\) つまり \(p^{2} = 2q^{2}\) が成り立つと仮定する。ここから \((2q - p)^{2} = 2(p - q)^{2}\) が分かるので、\((2q - p)/(p - q)\) もまた同じ性質を持つ。しかし明らかに \(q \lt p \lt 2q\) であり、したがって \(p - q \lt q\) となる。よって \(p/q\) に等しく分母が \(q\) よりも小さい分数が存在するが、これは \(p/q\) が既約である仮定と矛盾する。
-
三乗が \(2\) に等しい有理数が存在しないことを示せ。
-
一般に、既約分数 \(p/q\) が有理数の三乗になるのは \(p\) と \(q\) が完全立方数である場合に限ることを示せ。
-
さらに一般化した命題は次の通りである。ガウスによって発見されたこの命題は、それまでに発見されていた様々な特殊ケースを含んでいる: 「整数係数の代数方程式 \[ x^{n} + p_{1}x^{n-1} + p_{2}x^{n-2} + \cdots + p_{n} = 0 \] は、整数でない有理数の根を持たない」 [この方程式が根 \(a/b\) を持つと仮定する。ここで \(a, b\) は共通因数を持たない二つの整数で、\(b\) は正とする。\(x\) に \(a/b\) を代入して両辺に \(b^{n-1}\) を乗じると次の等式を得る: \[ -\frac{a^{n}}{b} = p_{1}a^{n-1} + p_{2}a^{n-2}b + \cdots + p_{n}b^{n-1} \] 左辺の分数は整数だから \(b = 1\) であり、元の方程式の根は \(a\) と分かる。さらに \(a\) が \(p_{n}\) を割り切ることも分かる]
-
前問の方程式で \(p_{n} = 1\) かつ \[ \begin{gathered} 1 + p_{1} + p_{2} + p_{3} + \cdots, \\ 1 - p_{1} + p_{2} - p_{3} + \cdots \hphantom{,} \end{gathered} \] がどちらも \(0\) でないとき、方程式が有理根を持たないと示せ。
-
次の方程式に有理根があれば全て求めよ: \[ x^{4} - 4x^{3} - 8x^{2} + 13x + 10 = 0 \] [根は整数でしかありえず、可能性があるのは \(±1,\ ±2,\ ±5,\ ±10\) だけである。どれが根かは実際に計算すれば分かる。同様の方法を使えばこういった形をした任意の方程式の有理根を判定できる]
-
この処理が常に行えるという仮定はアルキメデスの公理 (Axiom of Archimedes) と呼ばれる命題と同値である。[return]