第五章 連続関数の極値と連続性
§89 \(x → ∞\) の極限
連続実変数の関数に話を戻そう。これからは一価関数だけに話を限定し1、考える関数を \(\phi(x)\) とする。\(x\) が基準直線 \(\Lambda\) 上の全ての点に対応する値を順に取るとして、考える点が固定された点から右に向かって止まることなく移動する様子を考える。このような状況を「\(x\) が無限大に向かう」あるいは「\(x\) が \(\infty\) に向かう」と言い、\(x \to \infty\) と表す。前章で議論した「\(n\) が \(\infty\) に向かうとき」との唯一の違いは、\(x\) が \(\infty\) に向かうときに全ての値を取る点にある。つまり \(x\) が \(\infty\) に向かうとき、\(x\) として考える値には \(\Lambda\) 上で最初の点から右にある全ての点が対応する。これに対して \(n\) が \(\infty\) に向かうときは対応する点が飛び飛びだった。この事実を「\(x\) は連続的に (continuously) \(\infty\) に向かう」と表現する。
前章の最初で説明したように、\(x\) の関数と \(n\) の関数には非常に密接な対応関係がある。例えば全ての \(n\) の関数は \(x\) の関数の整数に対応する値を取ってきたものとみなせる。\(n\) が \(\infty\) に向かうときの \(\phi(n)\) の振る舞いを特徴付ける特殊な性質を前章で見た。この章では同じ問題を \(\phi(x)\) について考えるが、登場する定義や定理は前章の繰り返しとなる。例えば §58 の定義には次の定義が対応する:
\(x\) が \(\infty\) に向かうときに 関数 \(\phi(x)\) が極限 \(l\) に向かうとは、任意の正の実数 \(\varepsilon\) について、\(\varepsilon\) がどれだけ小さくとも、\(x_{0}(\varepsilon)\) 以上の全ての \(x\) について \(\phi(x)\) と \(l\) の差が \(\varepsilon\) より小さい、つまり \[ |\phi(x) - l| \lt \varepsilon \] が成り立つように \(x_{0}(\varepsilon)\) を選べることを言う。
このとき次のように書く: \[ \lim_{x \to \infty} \phi(x) = l \] 意味が曖昧にならないなら \(\lim\phi(x) = l\) あるいは \(\phi(x) \to l\) と書く場合もある。また次の定義も得られる:
関数 \(\phi(x)\) が \(x\) と共に \(\infty\) に向かうとは、任意の実数 \(\Delta\) について、\(\Delta\) がどれだけ大きくとも、全ての \(x \geq x_{0}(\Delta)\) で \[ \phi(x) \gt \Delta \] が成り立つように \(x_{0}(\Delta)\) を選べることを言う。
このとき \[ \phi(x) \to \infty \] と書く。同様に \(\phi(x) \to -\infty\) も定義する2。最後に振動を定義する:
これまでの二つの定義のどちらにも当てはまらないとき、\(\phi(x)\) は \(x\) が \(\infty\) に向かうとき振動すると言う。\(x \geq x_{0}\) で \(|\phi(x)|\) が定数 \(K\) より小さいなら \(\phi(x)\) は有限に振動すると言い3、そうでないなら無限に振動するという。
前章では \(\phi(n) \to l\) や \(\phi(n) \to \infty\) という式と同じ事実を表すくだけた表現について非常に詳しく説明した。これからは第四章と同じ意味で「小さい」「ほぼ等しい」「大きい」といった言葉を使い、「\(x\) が大きいとき \(\phi(x)\) が \(l\) に小さい (ほぼ等しい)」などと言うことにする。
-
次の関数の \(x \to \infty\) における振る舞いを調べよ: \[ \dfrac{1}{x},\quad 1 + \dfrac{1}{x},\quad x^{2},\quad x^{k},\quad [x],\quad x - [x],\quad [x] + \sqrt{x - [x]} \]
最初の四つの関数は第四章で考えた \(n\) の関数と同様に振る舞う。最後の三つのグラフは 例 16 1, 2, 4 で考えた。\([x] \to \infty\) および \(x - [x]\) が有限に振動すること、そして \([x] + \sqrt{x - [x]} \to \infty\) はグラフから容易に分かる。
興味深い事実を一つ述べる。グラフから分かる通り関数 \(\phi(x) = x - [x]\) は \(0\) と \(1\) の間で振動する。しかし \(x\) が整数のとき \(\phi(x)\) は \(0\) なので、整数関数 \(\phi(n)\) は常に \(0\) であり、極限 \(0\) に向かう。また \[ \phi(x) = \sin x\pi,\quad \phi(n) = \sin n\pi = 0 \] でも同じ現象が起こる。つまり \(\phi(x) \to l\) や \(\phi(x) \to \infty\) あるいは \(\phi(x) \to -\infty\) なら \(\phi(n)\) も同じように振る舞うが、逆は決して成り立たない。
-
関数 \[ \frac{\sin x\pi}{x},\quad x\sin x\pi,\quad (x\sin x\pi)^{2},\quad \tan x\pi,\quad a\cos^{2} x\pi + b\sin^{2} x\pi \] のグラフを描いて、\(x \to \infty\) における振る舞いを求めよ。
-
連続関数に対する定義を §59 と同様に幾何学的に説明せよ。
-
\(\phi(x)\cos x\pi\) と \(\phi(x)\sin x \pi\) は \(\phi(x) \to l\) で \(l \neq 0\) ならどちらも有限に振動し、\(\phi(x) \to \infty\) または \(\phi(x) \to -\infty\) なら無限に振動する。二つの関数のグラフは二つの曲線 \(y = \phi(x)\) と \(y = -\phi(x)\) の間を振動する波状の曲線となる。
-
\(x \to \infty\) における次の関数の振る舞いを調べよ: \[ y = f(x)\cos^{2} x\pi + F(x)\sin^{2} x\pi \] \(f(x)\) と \(F(x)\) は単純な関数 (例えば \(x\) や \(x^{2}\)) とする。 [\(y\) のグラフは \(y = f(x)\) と \(y = F(x)\) の間を振動する曲線となる]
§90 \(x → -∞\) の極限
前節の内容を踏まえれば「\(x\) が \(-\infty\) に向かう」や「\(x \to \infty\)」あるいは式 \[ \lim_{x \to -\infty} \phi(x) = l,\quad \phi(x) \to \infty,\quad \phi(x) \to -\infty \] の意味は簡単に理解できるだろう。実際 \(x = -y\) および \(\phi(x) = \phi(-y) = \psi(y)\) とすれば \(x\) が \(-\infty\) に向かうとき \(y\) は \(\infty\) に向かうので、考えている \(x\) が \(-\infty\) に向かうときの \(\phi(x)\) の振る舞いは \(y\) が \(\infty\) に向かうときの \(\psi(y)\) の振る舞いに一致する。
§91 連続関数の極限に対する算術演算
第四章で証明した関数の和・積・商に関する定理は、連続変数 \(x\) の関数に対しても成り立つ (もちろん表現が多少変わるが、どれも自明だろう)。結論が似ているだけではなく、証明もほとんど同じとなる。
§92 連続関数の単調増加と単調減少
§69 に対応する定義を次に示す: \(x_{2} \gt x_{1}\) のとき常に \(\phi(x_{2}) \geq \phi(x_{1})\) なら、\(\phi(x)\) は単調増加だと言う。この条件が成り立つのがある \(x\) から後ろ、つまり \(x_{2} \gt x_{1} \geq x_{0}\) でのみという場合も多くある。§69 で示した定理は \(n\) を \(x\) に変えれば成り立ち、証明も言葉遣いを調整すれば同様となる。
\(x_{2} \gt x_{1}\) のとき常に \(\phi(x_{2}) \gt \phi(x_{1})\) で等号が成り立たないなら、\(\phi(x)\) は 狭義単調増加 (steadily increasing in the stricter sense) だと言う。この区別が重要になることもある (例えば §108–§109 )。
関数 \(x^{2} - x,\ x + \sin x,\ x + 2\sin x,\ x^{2} + 2\sin x,\ [x],\ [x] + \sin x\), \([x] + \sqrt{x - [x]}\) のそれぞれについて、\(x\) について単調増加かどうか (またはある \(x\) から後ろで単調増加か) を考えてみるとよい。これらの関数は全て \(x \to \infty\) のとき \(\infty\) に向かう。
§93 \(x → 0\) の極限
\(\phi(x)\) を \(\lim\limits_{x \to \infty} \phi(x) = l\) を満たす関数とする。\(y = 1/x\) として \[ \phi(x) = \phi(1/y) = \psi(y) \] と定めると、\(x\) が \(\infty\) に向かうとき \(y\) は極限 \(0\) に向かい、\(\psi(y)\) は極限 \(l\) に向かう。
ここで \(x\) を無視して、\(\psi(y)\) を \(y\) の関数とみなす。大きい \(x\) に対応する \(y\) の値、つまり \(0\) に近い \(y\) の値だけに限って考えると、\(y\) の値を小さく取ることで \(\psi(y)\) を好きなだけ \(l\) に近くできる。変数が無限大に向かうときの極限の定義を正確に言うと、\(\lim\phi(x) = l\) は任意の正の実数 \(\varepsilon\) がどれだけ小さくとも、\(x_{0}\) 以上の全ての \(x\) で \(|\phi(x) - l| \lt \varepsilon\) が成り立つように \(x_{0}\) を選べることを意味する。そしてこれは、\(y_{0}\) より小さい全ての \(y\) で \(|\psi(y) - l| \lt \varepsilon\) が成り立つように \(y_{0} = 1/x_{0}\) を選べることに等しい。
こうして次の定義が導かれる:
任意の実数 \(\varepsilon\) について、\(\varepsilon\) がどれだけ小さくとも、\(0 \lt y \leq y_{0}(\varepsilon)\) で \[ |\phi(y) - l| \lt \varepsilon \] が成り立つように \(y_{0}(\varepsilon)\) を選べるとする。このとき「\(y\) が正の方向から \(0\) に向かうとき \(\phi(y)\) は極限 \(l\) に向かう」と言い、次のように表記する: \[ \lim_{y \to +0} \phi(y) = l \]
任意の実数 \(\Delta\) について、\(\Delta\) がどれだけ大きくとも、\(0 \lt y \leq y_{0}(\Delta)\) で \[ \phi(y) \gt \Delta \] が成り立つように \(y_{0}(\Delta)\) を選べるとする。このとき「\(y\) が正の方向から \(0\) に向かうとき \(\phi(y)\) は \(\infty\)に向かう」と言い、次のように表記する: \[ \lim_{y \to +0}\phi(y) \to \infty \]
「\(y\) が負の方向から \(0\) に向かうとき \(\phi(y)\) は \(l\) に向かう」つまり「\(y \to -0\) のとき \(\lim\phi(y) = l\)」も同様に定義する。一つ目の定義中の \(0 \lt y \leq y_{0}(\varepsilon)\) を \(-y_{0}(\varepsilon) \leq y \lt 0\) に変更すればそれですむ。二つ目の定義についても同様に \(y \to -0\) のときの \[ \phi(y) \to -\infty \] を定義する。
もし \(\lim\limits_{y \to +0} \phi(y) = l\) かつ \(\lim\limits_{y \to -0}\phi(y) = l\) なら、省略して \[ \lim_{y \to 0} \phi(y) = l \] と書く。このケースは非常に重要なので、定義をきちんと書いておく:
任意の正の実数 \(\varepsilon\) について、\(\varepsilon\) がどれだけ小さくとも、絶対値が \(y_{0}(\varepsilon)\) 未満の \(0\) でない全ての実数 \(y\) で \(\phi(y)\) と \(l\) が \(\varepsilon\) 未満しか離れないように \(y_{0}(\varepsilon)\) を選べるとする。このとき「\(y\) が \(0\) に向かうとき \(\phi(y)\) は極限 \(l\) に向かう」と言い \[ \lim_{y \to 0} \phi(y) = l \] と表記する。
同様に、\(y \to +0\) と \(y \to -0\) の両方で \(\phi(y) \to \infty\) なら「\(y \to 0\) で \(\phi(y) \to \infty\)」と言う。また「\(y \to 0\) で \(\phi(y) \to -\infty\)」も同様に定義する。
最後に、\(y \to +0\) のとき \(\phi(y)\) が極限にも \(\infty\) にも \(-\infty\) にも向かわないとする。このとき「\(y \to +0\) のとき \(\phi(y)\) は (有限または無限に) 振動する」と言う。\(y \to -0\) の場合も同様に振動を定義する。
ここまでの定義では変数を \(y\) と表記してきたが、もちろん変数の記号は重要でない。\(y\) の代わりに全て \(x\) と書いても構わない。
§94 \(x → a\) の極限
\(y \to 0\) のとき \(\phi(y) \to l\) とする。このとき \[ y = x - a,\quad \phi(y) = \phi(x - a) = \psi(x) \] とおくと、\(y \to 0\) のとき \(x \to a\) および \(\psi(x) \to l\) となる。ここから \[ \lim_{x \to a} \psi(x) = l \] あるいは \(\lim\psi(x) = l\) や \(\psi(x) \to l\) という表記が自然に導かれる。このとき「\(x\) が \(a\) に向かうとき \(\psi(x)\) は極限 \(l\) に向かう」と言う。正確で直接的な定義を次に示す:
\(\varepsilon\) が与えられたときに、\(0 \lt |x - a| \leq \delta(\varepsilon)\) で \[ |\phi(x) - l| \lt \varepsilon \] が成り立つよう \(\delta(\varepsilon)\) を常に選べるなら、 \[ \lim_{x \to a} \phi(x) = l \] と表記する。
不等式 \(0 \lt |x - a| \leq \delta(\varepsilon)\) を \(a \lt x \leq a + \delta(\varepsilon)\) と置き換えて \(a\) より大きい \(x\) だけを考えることで、「\(x\) が右から \(a\) に向かうとき \(\phi(x)\) は \(l\) に向かう」という言い回しを定義できる。このとき \[ \lim_{x \to a+0} \phi(x) = l \] と書く。同じく \[ \lim_{x \to a-0} \phi(x) = l \] も定義する。この定義から、\(\lim\limits_{x \to a} \phi(x) = l\) が次の二つの命題と同値だと分かる: \[ \lim_{x \to a+0} \phi(x) = l, \quad \lim_{x \to a-0} \phi(x) = l \]
右からおよび左から \(x \to a\) のときの \(\phi(x) \to \infty\) と \(\phi(x) \to -\infty\) も同様に定義されるが、ここで詳しく書く必要はないだろう。\(a = 0\) で示した定義とほとんど同じであり、\(\phi(x)\) の \(x \to a\) における振る舞いは \(x - a = y\) としたときの \(y \to 0\) を考えれば分かる。
§95 近傍における単調増加と単調減少
\(a - \delta \lt x' \lt x'' \lt a + \delta\) のとき \(\phi(x') \leq \phi(x'')\) となる実数 \(\delta\) が存在するなら、\(\phi(x)\) は \(x = a\) の近傍で単調増加であると言う。
\(\phi(x)\) が \(a\) の近傍で単調増加のとき、\(x \lt a\) として \(y = 1/(a - x)\) とおく。\(x \to a-0\) のとき \(y \to \infty\) であり、\(\phi(x) = \psi(y)\) は常に \(\phi(a)\) 以下の \(y\) の単調増加関数となる。§92 から、\(\phi(x)\) が \(\phi(a)\) 以下の極限に向かうことが言える。この値を \[ \lim_{x \to a+0} \phi(x) = \phi(a+0) \] と書く。\(\phi(a-0)\) も同様に定義する。このとき明らかに \[ \phi(a-0) \leq \phi(a) \leq \phi(a+0) \] が成り立つ。同様の議論は単調減少関数についても行える。
等号が成り立たず \(a - \delta \lt x' \lt x'' \lt a + \delta\) のとき常に \(\phi(x') \lt \phi(x'')\) なら、\(\phi(x)\) は \(a\) の近傍で狭義単調増加であると言う。
§96 上限と下限、収束の一般原則
§80–§84 の議論は実変数 \(x\) の関数が極限 \(a\) に向かうときにも適用できる。特に \(\phi(x)\) が \(a\) を含んだ区間で有界である4 (\(a - \delta \leq x \leq a + \delta\) で \(H \lt \phi(x) \lt K\) となるよう \(\delta,\ H,\ K\) を取れる) 場合には、\(x \to a\) における \(\phi(x)\) の上極限 \(\Lambda\) と下極限 \(\lambda\) が定義でき、\(x \to a\) で \(\phi(x) \to l\) となる必要十分条件は \(\lambda = \Lambda = l\) となる。同様に収束の一般原則に対応する命題も得られる。つまり \(x \to a\) で \(\phi(x)\) が極限 \(l\) に向かうための必要十分条件は、正の実数 \(\varepsilon\) が与えられたときに \(0 \lt |x_{2} - a| \lt |x_{1} - a| \leq \delta(\varepsilon)\) なら \(|\phi(x_{2}) - \phi(x_{1})| \lt \varepsilon\) となるように \(\delta(\varepsilon)\) を選べることである。
-
\(x \to a\) で \[ \phi(x) \to l,\quad \psi(x) \to l' \] なら、\(\phi(x) + \psi(x) \to l + l',\ \phi(x)\psi(x) \to ll',\ \phi(x)/\psi(x) \to l/l'\) が成り立つ。最後のケースでは \(l' \neq 0\) とする。
[第四章の §63 などで示した定理が \(x \to \infty\) や \(x \to -\infty\) のときの \(x\) の関数でも成り立つことは §91 で見た。\(x = 1/y\) とすればこの結果を \(y\) の関数の \(y \to 0\) における極限に拡張でき、さらに \(y = z - a\) とすれば \(z \to a\) のときの \(z\) の関数に拡張できる。
ただしそれでも、上記の正式な定義から直接証明してみるとよい。例えば最初の結果の厳密な証明を得るには、§63 にある証明の \(n\) を \(x\) に、\(\infty\) を \(a\) に、\(n \geq n_{0}\) を \(0 \lt |x - a| \leq \delta\) にそれぞれ置き換える]
-
\(m\) が正の整数なら \(x \to 0\) のとき \(x^{m} \to 0\) となる。
-
\(m\) が負の整数なら \(x \to +0\) のとき \(x^{m} \to \infty\) であり、\(x \to +0\) のときは \(m\) の偶奇に応じて \(x^{m} \to +\infty\) または \(x^{m} \to -\infty\) となる。\(m = 0\) なら \(x^{m} = 1\) なので \(x^{m} \to 1\) となる。
-
\(\lim\limits_{x \to 0} (a + bx + cx^{2} + \cdots + kx^{m}) = a\) が成り立つ。
-
\(\alpha \neq 0\) なら \(\lim\limits_{x \to 0} \dfrac{a + bx + \cdots + kx^{m}}{\alpha + \beta x + \cdots + \kappa x^{\mu}} = \dfrac{a}{\alpha}\) となる。\(\alpha = 0\) で \(a \neq 0\) かつ \(\beta \neq 0\) なら、\(a\) と \(\beta\) の符号が一致しているとき \(x \to + 0\) で \(+\infty\) に向かい、そうでないとき \(-\infty\) に向かう。\(x \to -0\) の場合は逆になる。\(a\) と \(\alpha\) の両方が \(0\) のケースは 例 36.5 で扱う。\(a \neq 0\) で \(\alpha\) 以外の分母の項にも \(0\) が含まれる場合を議論せよ。
-
\(m\) が正または負の整数なら \(\lim\limits_{x \to a} x^{m} = a^{m}\) が成り立つ。ただし \(a = 0\) かつ \(m\) が負の場合は除く。 [\(m \gt 0\) なら \(x = y + a\) として問題 4 を適用する。\(m \lt 0\) なら問題 1 から従う。この結果から \(P(x)\) が多項式なら \(\lim P(x) = P(a)\) だと分かる]
-
\(R\) が有理関数で \(a\) が \(R\) の分母の根でないなら、\(\lim\limits_{x \to a} R(x) = R(a)\) が成り立つ。
-
\(m\) が有理数なら、\(a = 0\) かつ \(m\) が負の場合を除いて \(\lim\limits_{x \to a} x^{m} = a^{m}\) だと示せ。 [\(m\) が正なら §74 の不等式 (9) と (10) から従う。つまり \(mx^{m-1}\) と \(ma^{m-1}\) の大きい方を \(H\) とすれば、\(|x^{m} - a^{m}| \lt H|x - a|\) が成り立つ (参考: 例 28.4)。\(a\) が負なら \(x = -y,\ a = -b\) とすれば \[ \lim x^{m} = \lim (-1)^{m}y^{m} = (-1)^{m}b^{m} = a^{m} \] が成り立つ]
§97 よくある誤解
前節の例 4, 5, 6, 7, 8 を見たとき、そもそも証明が必要なのかと疑問に思うかもしれない。「\(x = 0\) や \(x = a\) を代入すればそれで終わりでは?」ということだ。そうすればもちろん \(a,\ a/\alpha,\ a^{m},\ P(a),\ R(a)\) が得られる。ここで何が間違っているのかを正確に理解しておくのは非常に重要なので、次の例に移る前にさらに説明しておく。
式 \[ \lim_{x \to 0} \phi(x) = l \] が考えているのは、\(x\) が \(\bm{0}\) でないが \(\bm{0}\) に非常に近い値を取るときの \(\phi(x)\) の値である5。\(x = 0\) のときの \(\phi(x)\) の値ではない。つまり上のように書いたとき、\(x\) が \(0\) にほぼ等しいときに \(\phi(x)\) が \(l\) にほぼ等しいことを私たちは主張しているのであって、\(x\) が実際に \(0\) に等しいときに何が起こるかについては何も言っていない。例えば \(\phi(x) = 0\) という式で定義される関数を考えると、明らかに \[ \lim\phi(x) = 0 \qquad \text{(1)} \] が成り立つ。ここで \(\psi(x)\) を、\(x = 0\) のとき \(\psi(x) = 1\) でそれ以外は \(\phi(x)\) と等しい関数として定義する。すると \[ \lim\psi(x) = 0 \qquad \text{(2)} \] が依然として成り立つ。\(x\) が \(0\) にほぼ等しいなら、\(\psi(x)\) は \(0\) にちょうど等しいからである。しかし \(\psi(0) = 1\) なので、この関数のグラフは \(x\) 軸が \(x = 0\) で突き出た形となり、この突き出た点が孤立点 \((0, 1)\) となる。式 (2) は、このグラフを正負を問わない適当な \(x\) に対応する点から \(x = 0\) に向かって移動したときに、縦座標が極限 \(0\) に向かうことを表している (実際には縦座標は常に \(0\) に等しい)。この事実は孤立点 \((0, 1)\) がどこにあろうと揺るがない。
この例は人工的すぎるのではないか、と思うかもしれない。しかし \(x = 0\) でこの例と同じような振る舞いをする簡単な式が存在する。例えば \[ \psi(x) = [1 - x^{2}] \] がそうである。ここで \([1 - x^{2}]\) は通常通り \(1 - x^{2}\) を超えない最大の整数を表す。\(x = 0\) なら \(\psi(x) = [1] = 1\) だが、\(0 \lt x \lt 1\) および \(-1 \lt x \lt 0\) なら \(0 \lt 1 - x^{2} \lt 1\) であり、\(\psi(x) = [1 - x^{2}] = 0\) が成り立つ。
次は第二章の §24 で議論した関数 \[ y = \frac{x}{x} \] を考える。この関数は \(0\) でない全ての \(x\) で \(1\) に等しい。しかし \(x = 0\) のとき \(y\) は \(1\) でない、それどころか定義さえされない。第二章で説明した通り、\(\phi(x)\) が \(x = 0\) で定義されるには \(\phi(x)\) を定義する式に \(x = 0\) を代入したものが意味を持つ必要がある。今考えている式に \(x = 0\) を代入すると \(0/0\) という意味のない式となるので、この関数は \(x = 0\) で定義されない。「分母と分子を \(x\) で割ればいいじゃないか」と思うかもしれないが、この操作は \(x = 0\) のとき行えない。よって \(y = x/x\) は基本的に \(y = 1\) という関数だが、唯一 \(x = 0\) に対しては定義されない。しかしそれでも \[ \lim \frac{x}{x} = 1 \] が成り立つ。\(x\) が \(0\) でない限り、\(x\) がどれだけ \(0\) に近くとも \(x/x\) が \(1\) と等しくなるからである。
同様に \(\phi(x) = \{(x + 1)^{2} - 1\}/x\) は \(x\) が \(0\) でないなら \(x + 2\) に等しく、\(x = 0\) では定義されない。それでも \(\lim\phi(x) = 2\) が成り立つ。
一方で、\(x\) が \(0\) に向かうときの \(\phi(x)\) の極限が \(\phi(0)\)、つまり \(x = 0\) における \(\phi(x)\) の値に等しくなる場合もある。例えば \(\phi(x) = x\) なら \(\phi(0) = 0\) かつ \(\lim\phi(x) = 0\) となる。実用的な視点から言うと、応用で扱う関数の多くはこの特徴を持つ。
-
\(\lim\limits_{x \to a} \dfrac{x^{2} - a^{2}}{x - a} = 2a\) が成り立つ。
-
\(0\) 含む任意の整数 \(m\) に対して \(\lim\limits_{x \to a}\dfrac{x^{m} - a^{m}}{x - a} = ma^{m-1}\) が成り立つ。
-
問題 2 が全ての有理数 \(m\) に対して成り立つことを示せ。\(a\) は正とする。 [§74 の不等式 (9) と (10) から直ちに従う]
-
\(\lim\limits_{x \to 1}\dfrac{x^{7} - 2x^{5} + 1}{x^{3} - 3x^{2} + 2} = 1\) が成り立つ。 [分母と分子はどちらも \(x - 1\) を因子に持つ]
-
\(x\) が正の方向および負の方向から \(0\) に向かうときの関数 \[ \phi(x) = \frac{a_{0}x^{m} + a_{1}x^{m+1} + \cdots + a_{k}x^{m+k}} {b_{0}x^{n} + b_{1}x^{n+1} + \cdots + b_{l}x^{n+l}} \] の振る舞いを調べよ。
[\(m \gt n\) なら \(\lim\phi(x) = 0\)、\(m = n\) なら \(\lim\phi(x) = a_{0}/b_{0}\) となる。\(m \lt n\) で \(n - m\) が偶数なら、\(a_{0}/b_{0} \gt 0\) のとき \(\phi(x) \to +\infty\) で \(a_{0}/b_{0} \lt 0\) のとき \(\phi(x) \to -\infty\) となる。\(m \lt n\) で \(n - m\) が奇数なら、\(a_{0}/b_{0} \gt 0\) のとき \(x \to +0\) で \(\phi(x) \to +\infty\) および \(x \to -0\) で \(\phi(x) \to -\infty\)、\(a_{0}/b_{0} \lt 0\) のとき \(x \to +0\) で \(\phi(x) \to -\infty\) および \(x \to -0\) で \(\phi(x) \to +\infty\) となる]
-
小ささの次元: \(x\) が小さいとき、\(x^{2}\) はさらに小さく、\(x^{3}\) はそれ以上に小さい。以下同様であり \[ \lim_{x\to 0} \frac{x^{2}}{x} = 0,\quad \lim_{x\to 0} \frac{x^{3}}{x^{2}} = 0,\quad \ldots \] が成り立つ。
この事実を言い換えると次のようになる: \(x\) が \(0\) に向かうとき \(x^{2},\ x^{3},\ \ldots\) も \(0\) に向かうが、その速度は \(x^{2}\) の方が \(x\) よりも速く、\(x^{3}\) は \(x^{2}\) よりも速い。\(x \to 0\) のとき \(0\) に向かう関数について、値が小さくなる速度を測る方法があると便利である。測定の尺度は \(x,\ x^{2},\ x^{3}\) とするのが自然だろう。
そこで \(\phi(x)/x\) が \(x \to 0\) のとき \(0\) でない極限に向かうなら「\(\phi(x)\) は一次の小ささ (the first order of smallness) を持つ」と言うことにする。例えば \(\lim(2x + 3x^{2} + x^{7})/x = 2\) なので、\(2x + 3x^{2} + x^{7}\) は一次の小ささを持つ。
同様に二次\(\cdot\)三次\(\cdot\)四次\(\cdots\)の小ささを定義する。ただしこの小ささの次元が完全だと思ってはいけない。もしこの次元が完全なら、\(x\) と共に \(0\) に向かう全ての関数 \(\phi(x)\) が一次またはそれ以上の次元の小ささを持つことになるが、これは明らかに正しくない。例えば \(x^{7/5}\) が \(0\) に向かう速度は \(x\) より速いが \(x^{2}\) より遅い。
有理数の小ささの次元を考えて、\(x^{7/5}\) が \(\frac{7}{5}\) 次の小ささを持つとすれば完全になるだろうと考えてもいけない。こういった次元も完全にならないことを後の章で見る。応用で重要となるのは上で定義した整数の小ささの次元だけなので、定義をさらに細かくする必要はほとんどない。
大きさの次元: \(x\) が小さいときに \(\phi(x)\) が (正または負に) 大きくなる場合にも同様の定義ができる。つまり \(x\) が \(0\) に向かうときに \(\phi(x)/x^{-k} = x^{k}\phi(x)\) が \(0\) でない極限に向かうなら、「\(x\) が小さいとき \(\phi(x)\) は \(k\) 次の大きさ (\(k\)th-order of greatness) を持つ」と言う。
この定義は \(x \to 0\) で定義されているが、\(x \to \infty\) や \(x \to a\) を使っても同じように定義できる。例えば \(x \to \infty\) のとき \(x^{k}\phi(x)\) が \(0\) でない極限に向かうなら、\(\phi(x)\) は \(x\) が大きいとき \(k\) 次の小ささを持つと言う。また \(x \to a\) のとき \((x - a)^{k}\phi(x)\) が \(0\) でない極限に向かうなら、\(\phi(x)\) は \(x\) が \(a\) にほぼ等しいとき \(k\) 次の大きさを持つと言う。
-
\(\lim\sqrt{1 + x} = \lim\sqrt{1 - x} = 1\) が成り立つ6。 [\(1 + x = y\) または \(1 - x = y\) を代入し、例 35.8 を使う]
-
\(\lim\dfrac{\sqrt{1 + x} - \sqrt{1 - x}}{x} = 1\) が成り立つ。 [分母と分子に \(\sqrt{1 + x} + \sqrt{1 - x}\) を乗じる]
-
\(m\) と \(n\) を正の整数とする。\(x \to 0\) における \[ \dfrac{\sqrt{1 + x^{m}} - \sqrt{1 - x^{m}}}{x^{n}} \] の振る舞いを調べよ。
-
\(\lim\dfrac{\sqrt{1 + x + x^{2}} - 1}{x} = \dfrac{1}{2}\) が成り立つ。
-
\(\lim\dfrac{\sqrt{1 + x} - \sqrt{1 + x^{2}}}{\sqrt{1 - x^{2}} - \sqrt{1 - x}} = 1\) が成り立つ。
-
次の関数のグラフを描け: \[ y = \dfrac{\dfrac{1}{x - 1} + \dfrac{1}{x - \dfrac{1}{2}} + \dfrac{1}{x - \dfrac{1}{3}} + \dfrac{1}{x - \dfrac{1}{4}}} {\dfrac{1}{x - 1} + \dfrac{1}{x - \dfrac{1}{2}} + \dfrac{1}{x - \dfrac{1}{3}} + \dfrac{1}{x - \dfrac{1}{4}}} \]
この関数は \(x \to 0\) で極限を持つか? [\(x = 1,\ \frac{1}{2},\ \frac{1}{3},\ \frac{1}{4}\) で \(y\) は定義されず、それ以外では \(y = 1\) となる。また \(x \to 0\) のとき \(y \to 1\) である]
-
\(\lim\dfrac{\sin x}{x} = 1\) が成り立つ。
[三角比の定義から、\(0 \lt x \lt \frac{1}{2}\pi\) のとき \[ \sin x \lt x \lt \tan x \] が成り立つ7。ここから \[ \cos x \lt \frac{\sin x}{x} \lt 1 \] つまり \[ 0 \lt 1 - \frac{\sin x}{x} \lt 1 - \cos x = 2\sin^{2} \dfrac{1}{2} x \] が分かる。
ここで \(2\sin^{2} \dfrac{1}{2} x \lt 2(\dfrac{1}{2} x)^{2} = \dfrac{1}{2} x^{2}\) が成り立つので、\(\lim\limits_{x \to +0} \left(1 - \dfrac{\sin x}{x}\right) = 0\) つまり \(\lim\limits_{x \to +0} \dfrac{\sin x}{x} = 1\) が成り立つ。\(\dfrac{\sin x}{x}\) は偶関数だから、示すべき結果が得られる]
-
\(\lim \dfrac{1 - \cos x}{x^{2}} = \dfrac{1}{2}\) が成り立つ。
-
\(\lim \dfrac{\sin \alpha x}{x} = \alpha\) が成り立つ。これは \(\alpha = 0\) でも成り立つか?
-
\(\lim \dfrac{\arcsin x}{x} = 1\) が成り立つ。 [\(x = \sin y\) とする]
-
\(\lim \dfrac{\tan \alpha x}{x}= \alpha\) および \(\lim\dfrac{\arctan \alpha x}{x} = \alpha\) が成り立つ。
-
\(\lim \dfrac{\cosec x - \cot x}{x} = \dfrac{1}{2}\) が成り立つ。
-
\(\lim\limits_{x \to 1} \dfrac{1 + \cos \pi x}{\tan^{2}\pi x} = \dfrac{1}{2}\) が成り立つ。
-
\(x \to 0\) のとき関数 \(\sin(1/x),\ (1/x)\sin(1/x),\ x\sin(1/x)\) はどのように振る舞うか? [それぞれ有限に振動する、無限に振動する、極限 \(0\) に向かう。三つとも \(x = 0\) では定義されない。例 25.6 を使う]
-
\(x\) が \(0\) に向かうとき、関数 \[ y = \dfrac{\sin \frac{1}{x}}{\sin \frac{1}{x}} \] は極限に向かうか? [向かわない。この関数は基本的に \(1\) に等しいが、\(\sin(1/x) = 0\) のとき、つまり \(x = 1/\pi,\ 1/2\pi,\ \ldots,\ -1/\pi,\ -1/2\pi,\ \ldots\) のときは \(0/0\) となって定義されない。よって \(x = 0\) の近くの無限個の \(x\) に対して \(y\) が値を持たない]
-
\(m\) を整数とする。\(x \to m+0\) のとき \([x] \to m\) および \(x - [x] \to 0\) だと示し、さらに \(x \to m-0\) のとき \([x] \to m - 1\) および \(x - [x] \to 1\) だと示せ。
§98 実変数関数の連続性 (その 1)
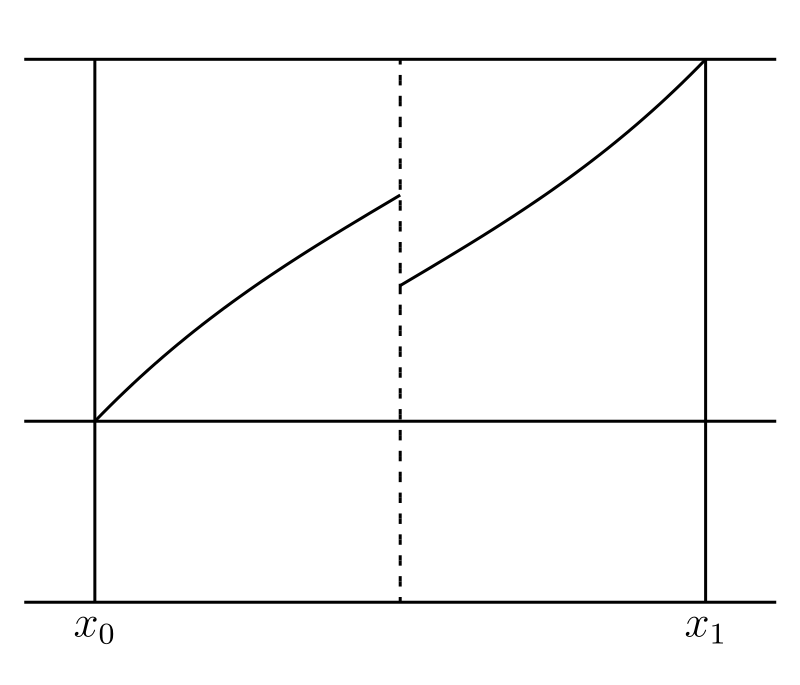
読者は連続曲線 (continuousc curve) という言葉を意味をおおまかに理解していると思う。例えば 図 29 の \(C\) は連続で、\(C'\) は基本的に連続だが \(x = \xi'\) と \(x = \xi''\) で不連続となっている。
いずれにせよ任意の曲線は何らかの関数 \(\phi(x)\) のグラフとみなせる。とすれば、グラフが連続曲線となる関数を連続 (continuous) と呼び、そうでなければ不連続と呼ぶのが自然である。しばらくの間これが連続性の定義だとみなして、この性質から導かれる性質について詳しく見ていく。
まず曲線 \(C\) をグラフに持つ関数 \(y = \phi(x)\) の性質は、曲線上の各点が持つ性質から分かると言える。つまり全ての \(\bm{x}\) に対する連続性を定義するには、まずある点 \(\bm{x}\) に対する連続性を定義する必要がある。そこで \(x = \xi\) として \(x\) の値を固定して \(\xi\) に対応するグラフ上の点を \(P\) とする。この \(x\) の値に対応する \(\phi(x)\) が持つ特徴的な性質は何だろうか?
何よりもまず \(\bm{\phi(x)}\) が \(\bm{x = \xi}\) で定義される必要がある。これは明らかに必要であり、もし \(\phi(\xi)\) が定義されていないと曲線に穴が開いてしまう。
次に\(\bm{\phi(x)}\) が \(\bm{x = \xi}\) の近くの全ての \(\bm{x}\) で定義されている必要もある。言い換えると、全ての点で \(\phi(x)\) が定義されるような \(x = \xi\) を含んだ区間が存在しなければならない。
最後に \(\bm{x}\) が \(\bm{\xi}\) に近づくとき、左右どちらから近づいたとしても \(\bm{\phi(x)}\) が \(\bm{\phi(\xi)}\) に近づく必要がある。
私たちが常識的に連続曲線とみなすものが持っている性質はこれで全てではない。上述の三つの性質は直線や円といった特殊な曲線から一般化したものに過ぎない。しかしそれでも、これらは最も基礎的で最も単純な性質である。つまりこの三つの性質を持つ任意の関数のグラフは (実際に描ける限り) 私たちが連続曲線の見た目について抱く印象を持っている。そこでこの三つの性質が数学的な連続性の概念を表すとして、次の定義を得る:
\(\phi(x)\) が \(x = \xi\) で連続とは、\(x\) が \(\xi\) に向かうときの極限が両方の側について存在して、どちらの極限も \(\phi(x)\) に等しいことを言う。
次に区間内での連続性を定義する。とある \(x\) の区間内で \(\phi(x)\) が連続とは、区間内の全ての \(x\) で \(\phi(x)\) が連続なことを言う。また全ての \(x\) で \(\phi(x)\) が連続なら、\(\phi(x)\) は いたるところで連続 (continuous everywhere) と言う。例えば \([x]\) は \(\frac{1}{2}\) より小さい任意の正の実数 \(\delta\) に対する区間 \([\delta, 1 - \delta]\) で連続であり、\(1\) と \(x\) は両方ともいたるところで連続となる。
極限の定義に戻って書き直すと、連続性の定義は「\(\phi(x)\) が \(x = \xi\) で連続とは、\(\varepsilon \gt 0\) が与えられたときに、\(0 \leq |x - \xi| \leq \delta(\varepsilon)\) のとき \(|\phi(x) - \phi(\xi)| \lt \varepsilon\) となるよう \(\delta(\varepsilon)\) を選べることを言う」となる。
区間 \([a, b]\) でだけ定義される関数を考えることあるが、このときには点 \(a\) と \(b\) における連続性の定義を少しだけ変更する必要がある。つまり \(x = a\) では \(\phi(a + 0)\) が存在して \(\phi(x)\) に等しいこと、\(x = b\) では \(\phi(b - 0)\) が存在して \(\phi(b)\) に等しいことをもって連続と言う。
§99 実変数関数の連続性 (その 2)
前節で示した連続性の定義は次のように図示できる。二つの水平な直線 \(y = \phi(\xi) - \varepsilon\) と \(y = \phi(\xi) + \varepsilon\) を描く。すると不等式 \(|\phi(x) - \phi(\xi)| \lt \varepsilon\) は \(x\) に対応する曲線上の点がこの二つの直線の間にあることを意味する。同様に不等式 \(|x - \xi| \leq \delta\) は \(x\) が区間 \([\xi - \delta, \xi + \delta]\) にあることを意味する。つまり連続性の定義は、二つの水平な直線を描いたときにその幅がどれだけ小さくとも、曲線を二つの垂直な直線で切って、その切り取られた曲線全体が二つの水平な直線の間に収まるようにできることを意味する。これは 図 29 の曲線 \(C\) でも正しい (\(\xi\) をどこに取っても構わない)。

ここからは様々な関数の連続性を個別に議論する。第二章ではこの結果の一部を仮定していた。
-
とある点で連続な二つの関数の和と積は、同じ点で連続となる。また商も分母が \(0\) にならない限り連続となる。 [例 35.1 から直ちに従う]
-
全ての多項式は全ての \(x\) で連続である。全ての有理関数は分母が \(0\) になる \(x\) を除いた全ての \(x\) で連続である。 [例 35.6 を使う]
-
\(\sqrt{x}\) は全ての正の \(x\) で連続である (例 35.8)。\(x \lt 0\) のときには定義されないが、\(x = 0\) では §98 の最後で定めた意味で連続となる。正整数 \(m\) と正の偶数 \(n\) に対する \(x^{m/n}\) でも同じことが成り立つ。
-
奇数 \(n\) に対する \(x^{m/n}\) は全ての \(x\) で連続である。
-
\(1/x\) は \(x = 0\) で連続でない。\(1/x\) は \(x = 0\) で値を持たず、さらに \(x \to 0\) のときの極限も持たない。具体的には \(x \to +0\) なら \(1/x \to +\infty\) で、\(x \to -0\) なら \(1/x \to -\infty\) となる。
-
\(m,\ n\) を正整数とする。\(x^{-m/n}\) の \(x = 0\) における連続性を調べよ。
-
有理関数の標準形 \(R(x) = P(x)/Q(x)\) は \(Q(x) = 0\) の根 \(a\) で不連続となる。例えば \((x^{2} + 1)/(x^{2} - 3x + 2)\) は \(x = 1\) で不連続である。有理関数が不連続となる点を考えると、(a) \(x\) でその値は定義されず、かつ (b) \(x\) がその値に近づくとき、どちらから近づいても \(+\infty\) または \(-\infty\) となる。こういった種類の不連続点を関数の無限点 (infinity) と呼ぶことがある。この "無限点" は私たちが普通に扱う関数において最もよく登場する不連続性である。
-
次の関数の連続性を調べよ: \[ \sqrt{(x - a)(b - x)},\quad \sqrt[3]{(x - a)(b - x)}, \] \[ \sqrt{(x - a)/(b - x)},\quad \sqrt[3]{(x - a)/(b - x)} \]
-
\(\sin x\) と \(\cos x\) は全ての \(x\) で連続である。
[次の等式が成り立つ: \[ \sin(x + h) - \sin x = 2\sin \dfrac{1}{2}h \cos(x + \dfrac{1}{2}h) \] これは \(h\) の絶対値より小さい]
-
\(\tan x,\ \cot x,\ \sec x,\ \cosec x\) が連続および不連続となる \(x\) の値は何か?
-
\(f(y)\) が \(y = \eta\) で連続とする。\(x\) の連続関数 \(\phi(x)\) が \(\phi(\xi) = \eta\) を満たすなら、\(f(\phi(x))\) は \(x = \xi\) で連続となる。
-
\(\phi(x)\) が全ての \(x\) で連続なら、\(\phi(x)\) の多項式 (例えば \(a\{\phi(x)\}^{m} + \cdots\)) も連続となる。
-
次の関数の連続性を調べよ: \[ \frac{1}{a\cos^{2} x + b\sin^{2} x},\quad \sqrt{2 + \cos x}, \quad \sqrt{1 + \sin x},\quad \frac{1}{\sqrt{1 + \sin x}} \]
-
\(\sin \dfrac{1}{x},\ x\sin \dfrac{1}{x},\ x^{2}\sin \dfrac{1}{x}\) はどれも \(x = 0\) 以外で連続である。
-
\(x \neq 0\) で \(x\sin \dfrac{1}{x}\) と等しく \(x = 0\) で \(0\) となる関数は全ての \(x\) で連続である。
-
\([x]\) と \(x - [x]\) は整数の \(x\) で不連続となる。
-
関数 \([x^{2}],\ [\sqrt{x}\,],\ \sqrt{x - [x]},\ [x] + \sqrt{x - [x]},\ [2x],\ [x] + [-x]\) が不連続となる \(x\) の値は何か (それとも全ての \(x\) で連続か)?
-
不連続性の分類: ここまでの例から、不連続にもいくつか種類があることが分かる。
-
左および右から \(x\) が \(a\) に向かうとき \(\phi(x)\) が極限を持つ場合がある。§95 で説明したようにこの二つの極限は \(\phi(a - 0)\) と \(\phi(a + 0)\) と表記される。連続性のための必要十分条件は、\(\phi(x)\) が \(x = a\) て定義されてかつ \(\phi(a - 0) = \phi(a) = \phi(a + 0)\) となることである。不連続性が生じるケースが二つある。
-
\(\phi(a - 0)\) と \(\phi(a + 0)\) が一致しても、\(\phi(a)\) が定義されない、もしくは \(\phi(a)\) が \(\phi(a - 0)\) および \(\phi(a + 0)\) と異なる。例えば \(\phi(x) = x \sin(1/x)\) で \(a = 0\) だと \(\phi(0 - 0) = \phi(0 + 0) = 0\) となるが、\(x = 0\) で \(\phi(x)\) が定義されない。あるいは \(\phi(x) = [1 - x^{2}]\) で \(a = 0\) だと \(\phi(0 - 0) = \phi(0 + 0) = 0\) だが \(\phi(0) = 1\) となる。
-
\(\phi(a - 0)\) と \(\phi(a + 0)\) が一致しない。このとき \(\phi(a)\) は極限のどちらかに等しいか、いずれとも等しくないか、定義されないかである。\(\phi(x) = [x]\) とすると \(\phi(0 - 0) = -1,\ \phi(0 + 0) = \phi(0) = 0\) となって最初のケースが得られる。\(\phi(x) = [x] - [-x]\) とすると \(\phi(0 - 0) = -1,\ \phi(0 + 0) = 1,\ \phi(0) = 0\) となって二つ目のケースとなる。\(\phi(x) = [x] + x\sin(1/x)\) とすれば \(\phi(0 - 0)= -1,\ \phi(0 + 0) = 0\) かつ \(\phi(x)\) が定義されず、三つ目のケースとなる。
この二つの場合には、\(\phi(x)\) が \(x = a\) で単純な不連続性 (simple discontinuity) を持つと言う。この二つに加えて、\(\phi(x)\) が \(x = a\) より左または右でしか定義されない状況で \(\phi(a - 0)\) または \(\phi(a + 0)\) が存在するものの \(x = a\) で \(\phi(x)\) が定義されないか極限と値が異なる場合も単純な不連続性を持つと言う。
§95 からは、\(x = a\) の近傍で単調増加または単調減少の関数が \(x = a\) で不連続だったとしても、それは単純な不連続性にしかならないことが容易に分かる。
-
-
\(\phi(a - 0)\) と \(\phi(a + 0)\) のどちらかあるいは両方が存在せず、極限が存在しない方向から \(x\) が \(a\) に向かうとき \(\phi(x)\) が \(+\infty\) または \(-\infty\) に向かうという場合もある。このとき \(x\) がどの方向から \(a\) に近づいてたとしても \(\phi(x)\) は極限・\( +\infty\)・\(-\infty\) のいずれかに向かう。例えば \(\phi(x) = 1/x\) や \(\phi(x) = 1/x^{2}\) で \(a = 0\) とするとこのケースとなる。このとき \(\phi(x)\) は \(x = a\) で無限点 (infinity) だと言う (参考: 問題 7)。(1) と同様に、\(a\) に片側から近づくと \(\phi(x) \to +\infty\) または \(\phi(x) \to -\infty\) で、反対側では \(\phi(x)\) が定義されないという状況もこのケースに含める。
-
不連続点が単純な不連続性を持たず無限点でもない場合、その点は振動する不連続性 (oscillatory discontinuity) を持つと言う。例えば \(\sin(1/x)\) や \((1/x)\sin(1/x)\) は \(x = 0\) で振動する不連続性を持つ。
-
-
次の関数の \(x = 0\) における不連続性の性質を調べよ: \[ \frac{\sin x}{x},\quad [x] + [-x],\quad \cosec x,\quad \sqrt{\frac{1}{x}},\quad \sqrt[3]{\frac{1}{x}}, \quad \cosec\frac{1}{x},\quad \frac{\sin\frac{1}{x}}{\sin\frac{1}{x}} \]
-
\(x\) が無理数なら \(0\) で有理数なら \(1\) の関数 (例 16.10) は全ての \(x\) で不連続である。有理数に対してだけ定義された関数も全ての \(x\) に対して不連続である。
-
\(x\) が無理数のとき \(x\) で、有理数 \(p/q\) なら \(\sqrt{(1 + p^{2})/(1 + q^{2})}\) の関数 (例 16.11) は正および負の有理数で不連続だが、正の無理数で連続となる。
-
例 31 で考えた関数が不連続となる点を求めよ。その不連続点の性質は何か? [例として問題 5 の関数 \(y = \lim x^{n}\) を考える。\(y\) は \(-1 \lt x \leq 1\) でしか定義されず、\(-1 \lt x \lt 1\) では \(0\)、\(x = 1\) では \(1\) となる。よって \(x = 1\) と \(x = -1\) が単純な不連続性を持つ]
§100 連続関数の性質 (その 1)
§98 に示した連続性の概念が最も単純で最も自然なものとは思えないかもしれない。私たちが連続と言い表す概念を解析する方法をもう一つ示す。\(\phi(x)\) のグラフ上の点 \(A,\ B\) の座標をそれぞれ \((x_{0},\ \phi(x_{0})),\ (x_{1},\ \phi(x_{1}))\) とする。\(A\) と \(B\) の間を通る直線 \(\lambda\) を適当に取る。このとき常識的に考えると、連続な \(\phi(x)\) のグラフは \(\lambda\) を横切る。
この性質を連続曲線に固有の幾何学的性質とみなすなら、\(x\) 軸に平行な \(\lambda\) だけを考えたとしても一般性は失われないのは明らかである。ただ \(A\) と \(B\) の \(y\) 座標が同じになってはいけないので、議論の都合上 \(\phi(x_{1}) \gt \phi(x_{0})\) と仮定する。\(\lambda\) が直線 \(y = \eta\) で \(\phi_(x_{0}) \lt \eta \lt \phi(x_{1})\) を満たすなら、\(\phi(x)\) が \(\lambda\) を横切るとは、\(x_{0}\) と \(x_{1}\) の間にある \(x\) で \(\phi(x) = \eta\) が成り立つことを意味する。
つまり連続曲線 \(\phi(x)\) は次の性質を持たなければならないと結論できる: もし \[ \phi(x_{0}) = y_{0},\quad \phi(x_{1}) = y_{1} \] で \(y_{0} \lt \eta \lt y_{1}\) なら、\(\phi(x) = \eta\) を満たす \(x\) が \(x_{0}\) と \(x_{1}\) の間に存在する。言い換えると、\(x\) が \(x_{0}\) から \(x_{1}\) に動くときに、\(y\) が \(y_{0}\) から \(y_{1}\) までの全ての値を少なくとも一度ずつ取らなければならない。
§98 の意味で連続な \(x\) の関数 \(\phi(x)\) がこの性質を持つことを示そう。\(x_{0}\) の右側には \(\phi(x) \lt \eta\) が成り立つ \(x\) の区間が存在する: \(\phi(x) - \phi(x_{0}) \lt \eta - \phi(x_{0})\) なら \(\phi(x) \lt \eta\) だが、\(x = x_{0}\) で \(\phi(x)\) は連続なので \(x\) を \(x_{0}\) に十分近づければこの条件は成り立つ。同様に \(x_{1}\) の左側には \(\phi(x) \gt \eta\) が成り立つ \(x\) の区間がある。
\(x_{0}\) から \(x_{1}\) までの \(x\) を次のようにして二つのクラス \(L,\ R\) に分ける:
- クラス \(L\) には \(x_{0} \leq x \leq \xi\) を満たす全ての \(x\) で \(\phi(x) \lt \eta\) となる \(\xi\) を全て入れる。
- クラス \(R\) にはその他の \(x\) を全て入れる。つまり \(\phi(\xi) \geq \eta\) が成り立つか、\(x_{0}\) から \(\xi\) の間に \(\phi(x) \geq \eta\) となる \(x\) が存在する \(\xi\) を全て入れる。
すると \(L,\ R\) は §17 の定理の条件を満たすので、この組はとある実数の切断となる。この切断が表す実数を \(\xi_{0}\) とする。
まず \(\phi(\xi_{0}) \gt \eta\) と仮定する。このとき \(\xi_{0}\) は上クラスに含まれる。\(\xi_{0}\) より小さい全ての \(\xi'\) は \(L\) に含まれるので、\(\phi(\xi') \lt \eta\) が成り立つ。よって \(\phi(\xi_{0}) = \eta + k\) とすると \[ \phi(\xi_{0}) - \phi(\xi') \gt k \] となる。しかしこれは \(x = \xi_{0}\) における連続性と矛盾する。
次に \(\phi(\xi_{0}) = \eta - k \lt \eta\) と仮定する。すると \(\xi_{0}\) より大きい任意の \(\xi'\) は \(R\) に含まれるので、\(\phi(\xi') \geq \eta\) が成り立つか、\(\xi_{0}\) と \(\xi'\) の間にある \(\xi''\) で \(\phi(\xi'') \geq \eta\) が成り立つ。いずれの場合でも \(\xi_{0}\) に好きなだけ近い \(x\) であって \(\phi(x)\) から \(k\) 以上離れているものを見つけられるが、これは \(\phi(x)\) が \(x = \xi_{0}\) で連続という仮定と矛盾する。
よって \(\phi(\xi_{0}) = \eta\) が分かり、定理の証明が完了する。ここで証明すべき命題以上のことを示している点に注目してほしい。つまり \(\xi_{0}\) が \(\phi(x) = \eta\) となる最小の \(x\) であることが示されている。関数がある値となる \(x\) に最小値が存在するかどうかは一般の関数では明らかでないし、実は正しくない。しかし連続関数であればこれが成り立つ。
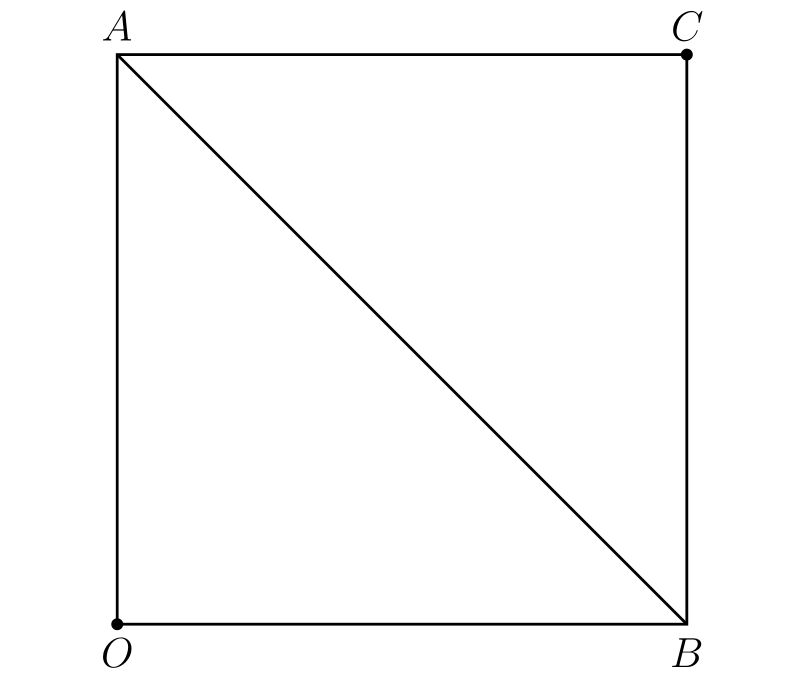
この定理の逆が正しくないことは容易に分かる。図 31 のグラフで表される関数 \(\phi(x)\) は \(\phi(x_{0})\) と \(\phi(x_{1})\) の間の全ての値を取るが、それでも \(\phi(x)\) は不連続である。さらに言えば、関数が全ての値をちょうど一度だけ取ると仮定してもなお \(\phi(x)\) は連続とならない。例えば \(\phi(x)\) を \(x = 0\) から \(x = 1\) で定義された関数として、\(x = 0\) で \(\phi(x) = 0\)、\(0 \lt x \lt 1\) で \(\phi(x) = 1 - x\)、\(x = 1\) で \(\phi(x) = 1\) とする。この関数のグラフは 図 32 のようになる。点 \(O,\ C\) はグラフに含まれるが、\(A,\ B\) は含まれない。明らかに \(x\) が \(0\) から \(1\) に移動するとき \(\phi(x)\) が \(\phi(0) = 0\) から \(\phi(1) = 1\) の全ての値をちょうど一度ずつ取るが、\(\phi(x)\) は \(x = 0\) と \(x = 1\) で不連続となる。
しかし実際のところ、初等数学に登場する曲線は \(\bm{y}\) が同じ方向に変化する曲線の有限個の集まりであることが多い。もし \(x\) が \(x_{0}\) から \(x_{1}\) まで動くとき \(y = \phi(x)\) が同じ方向に変化する、つまり \(\phi(x)\) が単調増加または単調減少なら、二つの連続の概念は一致する。つまり \(\phi(x)\) が \(\phi(x_{0})\) から \(\phi(x_{1})\) までの全ての値を取るなら、\(\phi(x)\) は §98 の意味で連続となる。証明を次に示す。\(\xi\) を \(x_{0} \lt \xi \lt x_{1} \) となるように取る。\(x\) が左から \(\xi\) に向かうとき \(\phi(x)\) は極限 \(\phi(\xi - 0)\) に向かう (§95)。同様に \(x\) が右から \(\xi\) に向かうとき \(\phi(x)\) は極限 \(\phi(\xi + 0)\) に向かう。関数が \(x = \xi\) で連続となる必要十分条件は \[ \phi(\xi - 0) = \phi(\xi) = \phi(\xi + 0) \] だった。もし一つ目の等式が成り立たないなら、\(\phi(x)\) は単調増加より \(\phi(\xi - 0)\) から \(\phi(\xi)\) の間の値を取らないことが分かるが、これは仮定と矛盾する。よって \(\phi(x)\) は連続だと分かる。以上の議論と前節の結果を合わせると、私たちが常識的に思い描く "連続" という概念がおおむね正確なこと、そして数学の言葉を使えばそれを正確に表せることが分かる。
§101 連続関数の性質 (その 2)
この節では連続関数に関する定理をさらにいくつか示す。
\(\phi(x)\) が \(x = \xi\) で連続とする。\(\phi(\xi)\) が正なら、区間 \([\xi - \delta, \xi + \delta]\) 全体で \(\phi(x)\) が正となるように正の実数 \(\delta\) を選べる。
証明は次の通り。連続性の定義における不等式で \(\varepsilon = \frac{1}{2}\phi(\xi)\) とすれば、ある \(\delta\) があって \[ |\phi(x) - \phi(\xi)| \lt \dfrac{1}{2}\phi(\xi) \] が \([\xi - \delta, \xi + \delta]\) で成り立つ。このとき \[ \phi(x) \geq \phi(\xi) - |\phi(x) - \phi(\xi)| \gt \dfrac{1}{2}\phi(\xi) \gt 0 \] だから、\(\phi(x)\) は正と分かる。\(\phi(x)\) が負のときにも同様の定理が成り立つ。
\(x = \xi\) で \(\phi(x)\) が連続とする。\(x\) を \(\xi\) に近づけることで \(\phi(x)\) の絶対値を好きなだけ小さくできるなら \(\phi(\xi) = 0\) となる。また \(\xi\) を含んだどれだけ小さい区間を考えても \(\phi(x)\) が正と負の値の両方を取るときも \(\phi(\xi) = 0\) となる。
これは一つ前の定理の系と言える。\(\phi(\xi) \neq 0\) なら \(\phi(\xi)\) は正または負となる。例えば正とすると \(\xi\) に十分近い全ての \(x\) で \(\phi(x)\) が正となるが、これは仮定に反する。
§102 連続関数の値域
区間 \([a, b]\) 内の全ての \(x\) で定義された \(\phi(x)\) を考える。これ以外の仮定は考えない。
\([a, b]\) に含まれる全ての \(x\) に対する \(\phi(x)\) の値を集めると、集合 \(S\) が構成される。この \(S\) には (§81 で \(n\) の関数に対して行ったように) §80 の議論を適用できる。例えば考えている全ての \(x\) について \(\phi(x) \leq K\) となる \(K\) が存在するなら、\(\phi(x)\) は上に有界 (bounded above) と言う。このとき、全ての \(\phi(x)\) は \(M\) 以下だが \(M\) より小さい任意の値に対してそれより大きい \(\phi(x)\) が少なくとも一つ必ず存在するという \(M\) がある。この \(M\) を上限 (supremum) と呼ぶ。連続変数 \(x\) の関数に対する下に有界、下限、有界の意味を同様に定義する。
\(\phi(x)\) が \([a, b]\) で連続なら \([a, b]\) で有界である。
証明は次の通り。\(\phi(x)\) が \(x = a\) で連続なので、任意の正の \(\varepsilon\) に対して、\(\varepsilon\) がどれだけ小さくとも、\(\phi(x)\) が \(\phi(a) - \varepsilon\) と \(\phi(a) + \varepsilon\) の間に収まる \(x\) の区間 \([a, \xi]\) が存在する。その区間では \(\phi(x)\) は有界なので、\(a\) から右に伸びる区間 \([a, \xi]\) であって \(\phi(x)\) が有界となるものが存在すると言える。
区間 \([a, b]\) に属する点 \(\xi\) を二つのクラス \(L,\ R\) に分割する。\(\phi(x)\) が \([a, \xi]\) で有界なら \(\xi\) を \(L\) に入れ、そうでないなら \(R\) に入れる。前段落の議論から \(L\) は存在すると分かるので、後は \(R\) が空だと示せばよい。\(R\) が空でないと仮定し、\(L\) と \(R\) の切断に対応する実数を \(\beta\) とする。\(\phi(x)\) は \(x = \beta\) で連続なので、任意に小さい正の実数 \(\varepsilon\) に対して \[ \phi(\beta) - \varepsilon \lt \phi(x) \lt \phi(\beta) + \varepsilon \] が成り立つ区間 \([\beta - \eta, \beta + \eta]\) が存在する8。\(\beta\) に関する仮定から \(\beta - \eta\) は \(L\) に属するので、\(\phi(x)\) は \([a, \beta - \eta]\) で有界と分かる。よって \(\phi(x)\) は区間 \([a, \beta + \eta]\) 全体で有界と結論できる。しかし \(\beta + \eta\) が \(R\) に属するので、\(\phi(x)\) は \([a, \beta + \eta]\) で有界でない。この矛盾から \(R\) が存在しないと分かる。つまり \(\phi(x)\) は区間 \([a, b]\) 全体で有界である。
\([a, b]\) で \(\phi(x)\) が連続で \(M\) と \(m\) がその上限と下限なら、\(\phi(x)\) は区間内で \(M\) と \(m\) を少なくとも一度ずつ取る。
証明は次の通り。与えられた任意の正の実数 \(\varepsilon\) に対して、\(M - \phi(x) \lt \varepsilon\) つまり \(1/\{M - \phi(x)\} \gt 1/\varepsilon\) となる \(x\) が存在する。よって \(1/\{M - \phi(x)\}\) は \([a, b]\) で有界でないので、一つ前の定理から不連続と分かる。一方 \(M - \phi(x)\) は連続関数であり、\(1/\{M - \phi(x)\}\) は分母が \(0\) にならない限り連続である (例 37.1)。よって分母が \(0\) となる点が存在し、この点で \(\phi(x) = M\) となる。同様に \(\phi(x) = m\) となる点も存在する。
これはどちらかと言うと手が込んでいて間接的な証明と言える。この定理はとても重要なので、後で別証明を示す9。
-
\(x \neq 0\) で \(\phi(x) = 1/x\)、\(x = 0\) で \(\phi(x) = 0\) とする。\(x = 0\) を含む任意の区間 (例えば \([-1, 1]\)) で \(\phi(x)\) は上限も下限も持たない。
-
\(x \neq 0\) で \(\phi(x) = 1/x^{2}\)、\(x = 0\) で \(\phi(x) = 0\) とする。区間 \([-1, +1]\) で \(\phi(x)\) は下限 \(0\) を持つが、上限は持たない。
-
\(x \neq 0\) で \(\phi(x) = \sin(1/x)\) 、\(x = 0\) で \(\phi(x) = 0\) とする。\(\phi(x)\) は \(x = 0\) で不連続であり、任意の区間 \([-\varepsilon, +\varepsilon]\) で下限 \(-1\) と上限 \(+1\) を持つ。その区間内に \(\phi(x)\) が上限および下限と等しくなる \(x\) は無限に存在する。
-
\(\phi(x) = x - [x]\) なら、この関数は整数の \(x\) で不連続となる。区間 \([0, 1]\) における \(\phi(x)\) の上限は \(1\) で下限は \(0\) である。\(x = 0\) で \(\phi(x)\) は \(0\) となるが、この区間で \(\phi(x)\) が \(1\) になることはない。つまり \(\phi(x)\) は上限と等しくならない。
-
\(x\) が無理数のとき \(\phi(x) = 0\)、\(x\) が有理数 \(p/q\) のとき \(\phi(x) = q\) とする。任意の区間 \([a, b]\) について \(\phi(x)\) の下限は \(0\) で上限は存在しない。また有理数 \(x = p/q\) に対して \(\phi(x) = (-1)^{p}q\) とした場合には \(\phi(n)\) は下限も上限も持たなくなる。
§103 区間内における関数の振動
\(\phi(x)\) を \([a, b]\) で有界な関数、\(M\) と \(m\) を \([a, b]\) における \(\phi(x)\) の上限と下限とする。\(M\) と \(m\) が \(a\) と \(b\) によって変化することを明示的に表すために、これから \(M\) と \(m\) を \(M(a, b)\) および \(m(a, b)\) と表記する。さらに \[ O(a, b) = M(a, b) - m(a, b) \] と定義し、この上限と下限の差 \(O(a, b)\) を \([a, b]\) における \(\phi(x)\) の 振動 (oscillation) と呼ぶことにする。\(M(a, b),\ m(a, b),\ O(a, b)\) の簡単な性質は次の通りである:
- \(a \leq c \leq b\) なら \(M(a, b)\) は \(M(a, c)\) と \(M(c, b)\) の大きい方と等しく、\(m(a, b)\) は \(m(a, c)\) と \(m(c, b)\) の小さい方と等しい。
- \(M(a, b)\) と \(O(a, b)\) は \(b\) の単調増加関数であり、\(m(a, b)\) は \(b\) の単調減少関数である。
- \(O(a, b) \leq O(a, c) + O(c, b)\) が成り立つ。
最初の二つは定義から直ちに得られる。\(M(a, c)\) と \(M(c, b)\) の大きい方を \(\mu\) として、任意の正の実数 \(\varepsilon\) を取る。すると \([a, c]\) と \([c, b]\)、つまり \([a, b]\) 全体で \(\phi(x) \leq \mu\) が成り立ち、さらに \([a, c]\) または \([c, b]\) のどこか、つまり \([a, b]\) のどこかで \(\phi(x) \gt \mu - \varepsilon\) が成り立つ。よって \(M(a, b) = \mu\) となる。\(m\) についても同じように示せる。(2) は (1) の系として得られる。
\(M(a, c)\) と \(M(c, b)\) の大きい方と小さい方をそれぞれ \(M_{1},\ M_{2}\) として、\(m(a, c)\) と \(m(c, b)\) の小さい方と大きい方をそれぞれ \(m_{1},\ m_{2}\) とする。すると \(c\) は両方の区間に含まれるから、\(\phi(c)\) は \(M_{2}\) 以下 \(m_{2}\) 以上である。よって \(M_{2}\) と \(m_{2}\) がどちらの区間から取られているかに関わらず \(M_{2} \geq m_{2}\) が成り立つ。ここから \[ O(a, b) = M_{1} - m_{1} \leq M_{1} + M_{2} - m_{1} - m_{2} \] が分かる。一方で \[ O(a, c) + O(c, b) = M_{1} + M_{2} - m_{1} - m_{2} \] だから、(3) が分かる。
§104 §102 の定理の別証明
§102 の二番目の定理の最も単純な証明を示す。\([a, b]\) に含まれる任意の実数を \(\xi\) とする。関数 \(M(a, \xi)\) は \(\xi\) に関して単調増加であり、かつ \(M\) を超えない。よって \(M(a, \xi) \lt M\) か \(M(a, \xi) = M\) かに応じて \(\xi\) を \(L\) と \(R\) に入れれば、切断を定義できる。この切断に対応する実数を \(\beta\) とする。\(a \lt \beta \lt b\) なら \[ M(a, \beta - \eta) \lt M,\quad M(a, \beta + \eta) = M \] が全ての正の実数 \(\eta\) に対して成り立つ。さらに §103 の \(\text{(1)}\) から \[ M(\beta - \eta, \beta + \eta) = M \] も分かる。つまり \(x\) が \(\beta\) に近ければ \(\phi(x)\) は \(M\) に好きなだけ近い値を取る。\(\phi(x)\) は連続だから、\(\phi(\beta)\) は \(M\) に等しくなければならない。
もし \(\beta = a\) なら \(M(a, a + \eta) = M\) で、\(\beta = b\) なら \(M(a, b-\eta) \lt M\) かつ \(M(b - \eta, b) = M\) となる。どちらの場合でも同様に議論できる。
この定理は §71 で使った区間の再帰的な分割による議論でも証明できる。区間 \(PQ\) における \(\phi(x)\) の上限が \(M\) なら、\(PQ\) を二等分すると少なくとも一方で \(\phi(x)\) の上限が \(M\) となる。これを \(P_{1}Q_{1}\) とすれば、§71 と同様に同じ処理を繰り返すことで \(\phi(x)\) の上限が \(M\) である区間 \(PQ,\ P_{1}Q_{1},\ P_{2}Q_{2},\ \ldots\) を取れる。§71 と同じ理由によりこの区間は点 \(T\) に収束し、この点において \(\phi(x)\) が \(M\) となることが示せる。
§105 ハイネ・ボレルの定理
続いて関数の振動に関する定理を証明する。この定理はいくらか抽象的だが非常に重要であり、特に後で見る積分の理論で使われる。この定理の証明には直線上の区間に関する一般的な定理が必要になる。
直線上の区間の集合、つまり各要素が区間 \([\alpha, \beta]\) である集まりが与えられたとする。区間の性質には制限を付けないので、区間の数が有限個でも無限個でもよく、区間同士が重なっていても構わないし10、互いに入れ子になっている可能性もある。
これから何度か使うので、区間の集合の例をいくつか示しておく。
- 区間 \([0, 1]\) を \(n\) 等分すると \(n\) 個の区間が得られる。これは互いに重ならない区間の集合であり、\([0, 1]\) を線分をちょうど覆う。
- 区間 \([0, 1]\) に含まれる任意の点 \(\xi\) を取り、\(\xi\) に区間 \([\xi - \delta, \xi + \delta]\) を対応させる。ここで \(\delta\) は \(1\) より小さい適当な正の実数とする。ただし \(0\) には \([1 - \delta, 1]\) を対応させ、区間 \([0, 1]\) の外側に飛び出した部分は無視する。すると区間の無限集合が定義され、この集合では無数の区間が互いに重なる。
- 区間 \([0, 1]\) に含まれる有理点 \(p/q\) を取り、\(p/q\) に \[ \left[\frac{p}{q} - \frac{\delta}{q^{3}}, \frac{p}{q} + \frac{\delta}{q^{3}}\right] \] を関連付ける。ここで \(\delta\) は \(1\) より小さい適当な正の実数で、\(0\) は \(0/1\)、\(1\) は \(1/1\) とみなし、\([0, 1]\) の外側は無視する。すると区間の無限集合が得られる。\(p/q\) に関連付けられる区間の中には \(p/q\) でない有理点が無限に含まれるので、区間は無限に重なる。
区間 \([a, b]\) と区間の集合 \(I\) が与えられ、\(I\) の全ての要素は \([a, b]\) に含まれるとする。さらに \(I\) が次の性質を持つとする:
- \([a, b]\) に含まれる \(a\) と \(b\) 以外の任意の点が、少なくとも一つの \(I\) の区間の内部にある11。
- \(a\) を左端に持つ区間と \(b\) を右端に持つ区間が少なくとも一つ \(I\) に含まれる。
このとき \(I\) に含まれる区間の有限集合であって性質 (1) と (2) を満たすものが存在する。
証明は次の通り。\(a\) は少なくとも一つの \(I\) の区間の左端だから、その区間を \([a, a_{1}]\) とする。\(a_{1}\) が \(I\) のある区間の内部にあることも分かっているので、その区間を \([a_{1}', a_{2}]\) とする。同様に \(a_{2}\) は \(I\) の区間 \([a_{2}', a_{3}]\) の内部にあると分かる。この議論は無限に繰り返せるが、有限回のステップで \(a_{n}\) が \(b\) になった場合にはそこで終わる。
有限回のステップで \(a_{n}\) が \(b\) になるなら、それまでに選んだ \(I\) の区間の有限集合が満たすべき二つの性質を満たすので証明が完了する。もし \(a_{n}\) が \(b\) にならないなら、点 \(a_{1},\ a_{2},\ a_{3},\ \ldots\) は (右に進んでいくので) 極限に向かわなければならない。しかし今の段階では、この極限の点は \([a, b]\) のどこかにあるとしか言えない。
上述の \(a\) から始まる処理を全ての可能なやり方で行い、可能な \(a_{1},\ a_{2},\ a_{3},\ \ldots\) の列を全て得たとする。このとき少なくとも一つの列が有限回のステップの後 \(b\) に到着することを次のように示せる。

\(a\) と \(b\) の間にある点 \(\xi\) について、可能性が二つある。一つはある列のある \(a_{n}\) より \(\xi\) が左にある場合で、もう一つはそうでない場合である。点 \(\xi\) をこの条件のどちらが成り立つかに応じて二つのクラス \(L\) と \(R\) に分ける。\([a, a_{1}]\) に含まれる全ての点は \(L\) に含まれるので、\(L\) は空でない。これから \(R\) が空であり、全ての点 \(\xi\) が \(L\) に含まれると示す。
\(R\) が空でないなら、\(R\) の左側が全て \(L\) となる。このとき二つのクラス \(L,\ R\) は区間 \([a, b]\) の切断となり、\([a, b]\) の間にある実数 \(\xi_{0}\) に対応する。点 \(\xi_{0}\) は \(I\) のとある区間の内部に属するので、この区間を \([\xi', \xi'']\) とする。すると \(\xi'\) は \(L\) に含まれるので、\(\xi'\) はある列のある \(a_{n}\) の左側にある。すると \([\xi', \xi'']\) が \([a_{n}', a_{n+1}]\) となる列 \(a_{1},\ a_{2},\ a_{3},\ \ldots\) が存在し、\(\xi''\) より左側にある点は全て \(a_{n+1}\) の左側にある。よって \(L\) に含まれる点で \(\xi_{0}\) より右にあるものが存在することになるが、これは \(R\) の定義と矛盾する。よって \(R\) は空である。
したがって全ての点 \(\xi\) は \(L\) に含まれる。\(b\) はとある \(I\) の区間の右端なので、この区間を \([b_{1}, b]\) とする。このとき \(b_{1}\) は \(L\) に含まれるので、ある列 \(a_{1},\ a_{2},\ a_{3},\ \ldots\) のある項 \(a_{n}\) で \(a_{n} \gt b_{1}\) が成り立つ。よって \(a_{n}\) に対応する区間 \([a_{n}', a_{n+1}]\) を \([b_{1}, b]\) に取り換えて列の第 \(n+1\) 項を \(b\) とすれば、この列に対応する区間の集合は前述の性質を持つ。よって定理は示された。
この節の最初で示した例にこの定理を適用すると次のようになる:
-
ここでは定理の前提が成り立たない。つまり \(I\) のどの区間も \(1/n,\ 2/n,\ 3/n,\ \ldots\) を内部に含まない。
-
ここでは定理の前提が成り立つ。点列 \(\delta,\ 2\delta,\ 3\delta,\ \ldots,\ 1 - \delta\) に対応する \[ [0, 2\delta], \quad [\delta, 3\delta], \quad [2\delta, 4\delta], \quad \ldots, \quad [1 - 2\delta, 1] \] という区間の有限集合が性質 (1) と (2) を満たす。
-
ここではハイネ・ボレルの定理を使うことで、\(\delta\) が十分小さいなら \([0, 1]\) に含まれる点で \(I\) の区間の内部に含まれない点が存在することを示せる。
もし \([0, 1]\) の端点を除いた全ての点が \(I\) の区間の内部に含まれるなら、\(I\) の区間の有限集合であって性質 (1) と (2) を持つものが存在し、そのとき区間の長さの和が \(1\) より大きくなる。\(I\) には長さが \(\delta\) の区間 (\(q = 1\) に対応する区間) が二つあり、\(q \neq 1\) に対しては長さ \(2\delta/q^{3}\) の区間が \((q - 1)\) 個ある。よって \(I\) に含まれる区間の任意の有限集合は、長さの和が次の級数の和の \(2\delta\) 倍より大きくならない: \[ 1 + \frac{1}{2^{3}} + \frac{2}{3^{3}} + \frac{3}{4^{3}} + \cdots \] しかし第八章の知識を使えばこれが収束すると示せる。つまり \(\delta\) が十分小さいとき、\([0, 1]\) の全ての点が \(I\) の区間に含まれるとすると矛盾が生じる。
この証明が示す必要のないことを示していると思うかもしれない。\(I\) の区間の長さの和が \(1\) 未満なのだから、\(I\) の区間に含まれない点が存在するのは明らかではないかということだ。しかしこの推論で使われている (区間の無限集合についての) 命題は明らかとは程遠く、厳密な証明には今示したようなハイネ・ボレルの定理を使った議論が必要になる。
§106 関数の振動に関する定理
ハイネ・ボレルの定理を使って、関数の振動に関する重要な定理を二つ示す。
\(\phi(x)\) が区間 \([a, b]\) で連続なら、\([a, b]\) を有限個の小区間 \([a, x_{1}],\ [x_{1}, x_{2}],\ \ldots,\ [x_{n}, b]\) に分割し、各小区間で \(\phi(x)\) の振動が与えられた値より小さくなるようにできる。
証明は次の通り。\(\xi\) を \(a\) と \(b\) の間にある任意の実数とする。\(\phi(x)\) は \(x = \xi\) で連続だから、条件「\(\phi(x)\) の振動が \(\varepsilon\) より小さい」が成り立つように区間 \([\xi - \delta, \xi + \delta]\) を取れる。この条件がある \(\delta\) で成り立つとき \(\delta\) より小さい任意の値に対しても条件が成り立つので、任意の \(\xi\) と任意の \(\varepsilon\) に対してこの条件を満たす区間が無限に存在する。どの \(\delta\) で条件が満たされるかは \(\xi\) によって変わるので、ある \(\xi\) に対する \(\delta\) が他の \(\xi\) で \(\delta\) になれるかは分からず、現段階では \(\delta\) は前もって取った \(\xi\) に対する条件を成り立せるとしか言えない。\(\xi\) に対応するこの区間を \(\xi\) の \(\bm{\varepsilon}\)-区間と呼ぶ。
\(\xi = a\) なら上述の性質を持った区間 \([a, a + \delta]\) が無数に取れるので、それらを \(a\) の \(\varepsilon\)-区間と呼ぶ。同様に \(b\) の \(\varepsilon\)-区間も定義する。
\([a, b]\) に含まれる全ての点に対する全ての \(\varepsilon\)-区間を集めて \(I\) とする。このとき \(I\) はハイネ・ボレルの定理の条件を満たす: 任意の点は \(I\) のある区間の内部の点であり、\(a\) と \(b\) を端点に持つ区間がある。よって \(I\) と同じくこの二つの性質を持つ \(I\) の区間の有限集合 \(I'\) が存在する。
\(I'\) に含まれる区間は一般に重なる (図 34)。しかしその端点を使って \([a, b]\) を有限個の区間の集合 \(I''\) に分割することはでき、そうすれば各区間内における \(\phi(x)\) の振動が \(\varepsilon\) より小さくなる。これで証明すべきことが示された。

区間 \([a, b]\) で連続な関数 \(\phi(x)\) と任意の正の実数 \(\varepsilon\) が与えられたとする。このとき \([a, b]\) を長さ \(\eta\) 未満の (複数の) 区間に分割すると各区間における \(\phi(x)\) の振動が \(\varepsilon\) 以下になるような \(\eta\) が存在する。
証明は次の通り。\(\varepsilon_{1} \lt \frac{1}{2}\varepsilon\) として、一つ前の定理から小区間の有限集合 \(j\) を得る。\(j\) の各区間では \(\phi(x)\) の振動が \(\varepsilon_{1}\) 以下となる。\(j\) に含まれる小区間の長さの最小値を \(\eta\) とする。\([a, b]\) を長さが \(\eta\) より小さい区間で分割すると、各区間は \(j\) の連続した区間を最大でも二つまたぐ。よって §103 の (3) から、この長さ \(\eta\) 未満の区間における \(\phi(x)\) の振動は \(j\) の小区間における \(\phi(x)\) の振動の最大値の二倍を超えない。つまり振動は \(2 \varepsilon_{1} = \varepsilon\) 未満となる。
この定理は第七章の定積分の理論で重要な役割を果たす。こういった定理がなければ、区間で連続な関数がその区間で積分できることを証明できない。
§107 連続な多変数関数
連続性と不連続性の概念は複数の独立変数を持つ関数 (§31) へ拡張できる。しかし多変数関数に対する連続性では、この章で考えたものよりずっと複雑な問題が生じる。この問題について詳しく述べようと思っても紙面が足りないが、二変数関数については後で考えることになるので、ここで定義を与えておく。これは §98 で最後に示した形の定義を一般化したものである。
二つの変数 \(x,\ y\) の関数 \(\phi(x, y)\) が \(x = \xi,\ y = \eta\) で連続とは、任意の正の実数 \(\varepsilon\) が与えられときに、\(\varepsilon\) がどれだけ小さくとも、\(0 \leq |x - \xi| \leq \delta(\varepsilon)\) かつ \(0 \leq |y - \eta| \leq \delta(\varepsilon)\) のとき \[ |\phi(x, y) - \phi(\xi, \eta) | \lt \varepsilon \] が成り立つように \(\delta(\varepsilon)\) を取れることを言う。つまり中心が \((\xi, \eta)\) で一辺の長さが \(2\delta(\varepsilon)\) の辺が軸に平行な正方形を考えたときに、その中の全ての点で \(\phi(x, y)\) と \(\phi(\xi, \eta)\) の差が \(\varepsilon\) 以下であることを言う12。
この定義は正方形の中の全ての点で \(\phi(x, y)\) が定義されていることを仮定している。特に \((\xi, \eta)\) での定義が必要となる。定義を別の方法で表現すると「\(\phi(x, y)\) が \(x = \xi,\ y = \eta\) で連続とは、\(x \to \xi,\ y \to \eta\) が近づき方に関わらず \(\phi(x, y) \to \phi(\xi, \eta)\) なことを言う」となる。一見するとこの定義の方が単純に見えるものの、この定義にはこれまでに正確な意味を定義していない言い回しが含まれており、それを説明するには最初の定義にあるような不等式を使うしかない。
連続な二変数関数の和・積・商が一般に連続になることは簡単に示せる。また二変数の多項式は全ての点で値において連続であり、通常の解析学で登場する \(x\) と \(y\) の関数も基本的には連続である。つまり \(x\) と \(y\) の間に特殊な関係があるときに限って不連続となる。
\(x\) と \(y\) という二つの変数に関する \(\phi(x, y)\) の連続性は、二つの変数を別々に考えたときの連続性とは異なる点によく注意しなければならない。\(\phi(x, y)\) が二つの変数 \(x\) と \(y\) の関数として連続なら、\(x\) (あるいは \(y\)) だけの関数についても連続となる。しかし逆は決して成り立たない。例えば \(x\) と \(y\) のどちらかが \(0\) でないとき \[ \phi(x, y) = \frac{2xy}{x^{2} + y^{2}} \] で \(x\) と \(y\) が両方 \(0\) のとき \(\phi(x, y) = 0\) とする。すると \(y\) の値を固定すれば、\(y\) が \(0\) であろうとなかろうと、関数 \(\phi(x, y)\) は連続な \(x\) の関数となる。例えば \(x = 0\) のときは \(\phi(x, y) = 0\) であり、\(x \to 0\) のときの極限も \(0\) なので連続となる。しかし \(x\) と \(y\) の関数 \(\phi(x, y)\) は \(x = 0,\ y = 0\) で不連続となり、連続でない。\(x\) と \(y\) が直線 \(y = ax\) 上から \(0\) に向かうとき、 \[ \phi(x, y) = \frac{2a}{1 + a^{2}},\quad \lim\phi(x, y) = \frac{2a}{1 + a^{2}} \] が成り立つ。つまり \(a\) を変化させれば極限が \(-1\) から \(1\) の全ての値を取る。
§108 陰関数定理
陰関数については前に第二章で説明した。例えば \(x\) と \(y\) が \[ y^{5} - xy - y - x = 0 \qquad \text{(1)} \] という関係で結ばれているなら、\(y\) は \(x\) の "陰関数" となる。
しかしこういった方程式が本当に \(x\) の関数 \(y\) を定義するかは証明なしには分からないし、複数の関数が定義される可能性もある。第二章では関数が定義されるのを当然として話を進めたが、ここまでの知識を使えばこれを正当化できる。
話を簡単にするために、用語を次のように定める。§107 と同様に、点 \((a, b)\) を囲む四角形であって特定の条件が成り立つものを考える。そのような四角形を \((a, b)\) の近傍 (neighborhood) と呼び、条件が \(\bm{(a, b)}\) の近傍で成り立つ、あるいは \(\bm{(a, b)}\) の近くで成り立つと言う。これは考えている条件が成り立つように四角形を一つ取れることだけを意味する。「直線上の区間」を「四角形」に置き換えれば、一変数の関数で使ったのと同じ言い回しが使える。
- \(x\) と \(y\) の関数 \(f(x, y)\) が \((a, b)\) の近傍で連続である
- \(f(a, b) = 0\)
- \(x\) が \(a\) の近傍にあるとき、\(f(x, y)\) が \(y\) の狭義単調増加関数 (§95) である
この三つの条件が成り立つとき、\(f(x, y) = 0\) に代入すると \(x\) が \(a\) の近傍にあるとき等式が常に成り立つような関数 \(y = \phi(x)\) がただ一つ存在する。さらに \(\phi(x)\) は \(a\) の近傍で常に連続である。
図 35 の四角形が条件 (i) と (iii) が成り立つ \((a, b)\) の近傍で、\(P\) が点 \((a, b)\) を表す。\(Q\) と \(R\) を図のように取ると、\(Q\) では \(f(x, y)\) が正で \(R\) では \(f(x, y)\) が負なことが (iii) から分かる。さらに \(f(x, y)\) が \(Q\) と \(R\) で連続なので、\(x\) 軸に平行な直線 \(QQ'\) と \(RR'\) を取ってその直線上で \(f(x, y)\) が常に正および負であるようにできる。特に \(Q'\) と \(R'\) で \(f(x, y)\) はそれぞれ正および負であり、(iii) と §100 から \(f(x, y)\) が \(0\) になる \(R'Q'\) 上の点 \(P'\) がただ一つ存在すると分かる。同様の議論を使えば \(RQ\) と \(R'Q'\) の間にある全ての垂直な直線上に \(f(x, y) = 0\) となる点を取れる。さらに \(RQ\) の左側にも点を取れるので、こういった点 \(P'\) を集めれば存在を示すべき関数 \(y = \phi(x)\) のグラフが得られる。
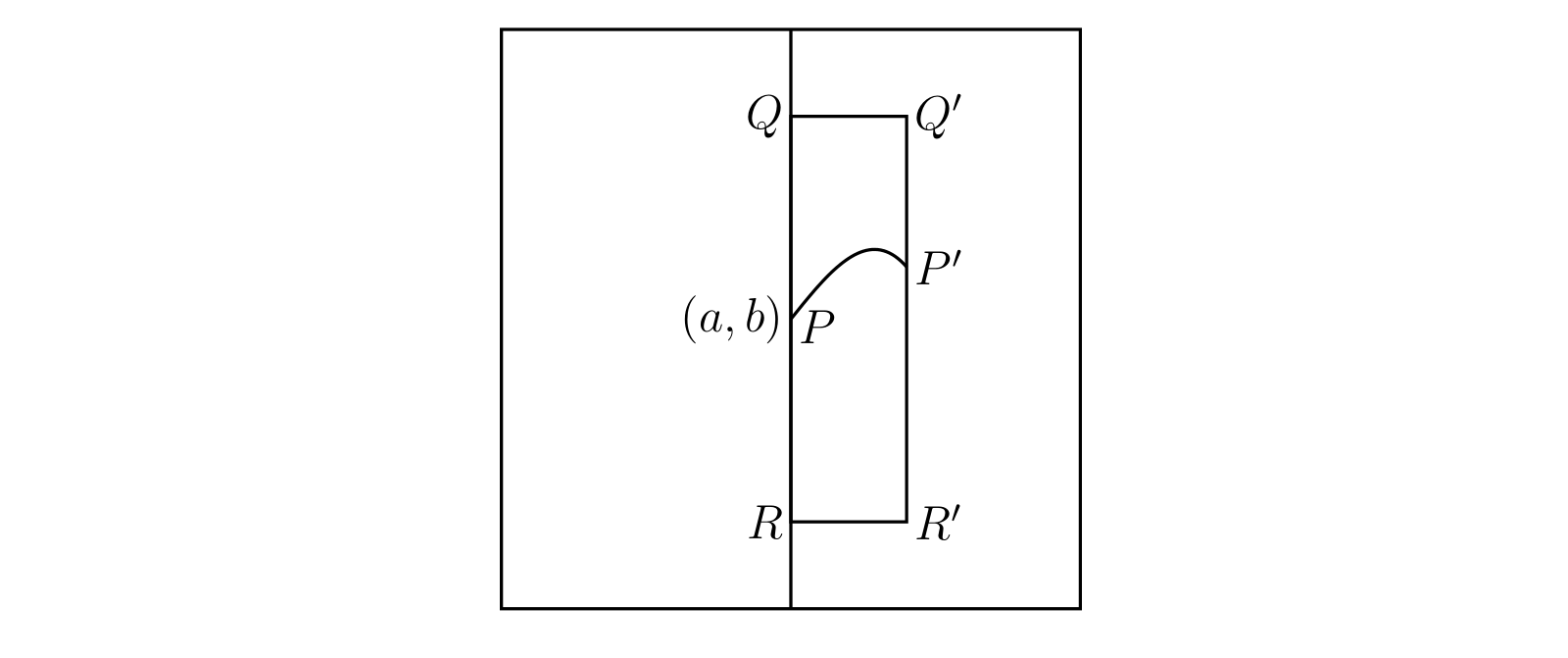
後は \(\phi(x)\) が連続だと示せばよい。\(x \to a\) における \(\phi(x)\) の上極限 \(\Lambda\) と下極限 \(\lambda\) (§96) を考えると議論が簡単になる。\((a, \lambda)\) は \(QR\) 上にあり、加えて \(x \to a\) で \(\phi(x) \to \lambda\) となるような \(x\) の値の列を見つけられる。\(f(x, \phi(x)) = 0\) で \(f(x, y)\) は \(x\) と \(y\) の連続関数なので \[ f(a, \lambda) = 0 \] が分かる。よって \(\lambda = b\) であり、同様に \(\Lambda = b\) も成り立つ。つまり \(x \to a\) のとき \(\phi(x)\) は極限 \(b\) に向かうので、\(\phi(x)\) は \(x = a\) で連続と分かる。\(x\) が \(a\) の近傍にあるときも同様に \(\phi(x)\) の連続性を示せる。
また定理の条件 (iii) の「狭義単調増加」を「狭義単調減少」に変えても結論は変わらないことも分かる。
例として、式 \(\text{(1)}\) で \(a = 0,\ b = 0\) とした場合を考える。条件 (i) と (ii) は明らかに成り立つ。加えて \[ f(x, y) - f(x, y') = (y - y') (y^{4} + y^{3}y' + y^{2}{y'}^{2} + y{y'}^{3} + {y'}^{4} - x - 1) \] は \(x,\ y,\ y'\) が小さいとき \(y - y'\) と逆の符号を持つので、条件 (iii) も (「増加」を「減少」として) 満たされる。ここから等式 \(\text{(1)}\) を恒等的に満たす連続関数 \(y\) であって \(x = 0\) で \(\phi(x) = 0\) を満たすものがあり、しかもそれは一つだけしか存在しないことが分かる。
次の等式を考えても同じ結論が得られる: \[ y^{2} - xy - y - x = 0 \] この場合、得られる関数は \[ y = \dfrac{1}{2}\{1 + x - \sqrt{1 + 6 x + x^{2}}\} \] となる。ただし根号は正の値を取るとする。もう一つの根号の値だと \(x = 0\) のとき関数の値が \(0\) にならない。
ここで気を付けるべき点がもう一つある。定理の条件に「\((a, b)\) の近傍」という言葉があるが、これはとある正方形 \(\xi - \delta \leq x \leq \xi + \delta,\ \eta - \delta \leq y \leq \eta + \delta\) を考えている。そして結論が成り立つのは \(x = a\) の近傍、つまり \(\xi - \delta_{1} \leq x \leq \xi + \delta_{1}\) という形の区間においてだけである。結論の \(\delta_{1}\) が条件の \(\delta\) と同じであるとは示されていないし、一般的に言って同じにならない。
§109 逆関数
前節の定理で \(f(x, y)\) を \(F(y) - x\) とすると、次の結果が得られる。
\(y\) の関数 \(F(y)\) が \(y = b\) の近傍で連続かつ (§95 の意味で) 狭義単調増加 (あるいは減少) で、\(F(b) = a\) だとする。このとき \(x = a\) で \(b\) に等しく、かつ \(x = a\) の近傍で \(F(y) = x\) が恒等的に成り立つ関数 \(y = \phi(x)\) がただ一つ存在する。
こうして定義される関数を \(F(y)\) の逆関数と呼ぶ。
例えば \(y^{3} = x,\ a = 0,\ b = 0\) とすると定理の条件は全て満たされ、逆関数は \(x = \sqrt[3]{y}\) となる。
一方で \(y^{2} = x\) とすると定理の条件が成り立たない。\(y^{2}\) は \(y\) が負のとき単調減少で正のとき単調増加なので、\(0\) を含んだ任意の区間で \(y^{2}\) は単調とならない。この場合定理の結論は成り立たず、\(y^{2} = x\) は \(x\) の関数を二つ定義する。具体的には \(y = \sqrt{x}\) と \(y = -\sqrt{x}\) であり、これらはどちらも \(x = 0\) で \(0\) となり、正の \(x\) に対してだけ定義される。これは方程式が二つの解を持つこともあれば解を持たないこともある事実に対応する。一般的な方程式 \[ y^{2n} = x, \quad y^{2n+1} = x \] についても考察してみるとよい。方程式 \[ y^{5} - y - x = 0 \] も興味深い例となる。これについては前に 例 14.7 で考えた。
同様に方程式 \[ \sin y = x \] は \(x = 0\) のとき \(0\) となる解を一つしか持たない。つまり \(x = 0\) で \(0\) になる \(\arcsin x\) である。他の \(\arcsin x\) の値を取れば方程式を満たす関数は無限に得られる (例 15.10) が、\(x = 0\) のとき \(0\) という条件を満たす解は一つしかない。
ここまでは特定の \(x\) の近傍で何が起こるかを見てきた。次は \(F(y)\) がとある区間 \([a, b]\) 全体で単調増加 (あるいは減少) と仮定する。\([a, b]\) に含まれる任意の点 \(\xi\) について \(\xi\) を含んだ区間 \(i\) を取ることができ、\(i\) で連続な唯一の逆関数 \(\phi_{i} (x)\) が存在する。
区間 \(i\) を集めて \(I\) とすれば、ハイネ・ボレルの定理から \([a, b]\) を被覆する \(I\) の区間の有限集合を見つけられる。するとその集合に含まれる \(i\) に対応する関数 \(\phi_{i} (x)\) の集合は、\([a, b]\) 全体で連続な逆関数 \(\phi(x)\) を定義する。
こうして次の定理が得られる:
\(x = F(y)\) を単調増加な連続関数とする。\(x\) が \(a\) から \(b\) に増加するとき \(y\) が \(A\) から \(B\) へ増加するなら、連続な逆関数 \(y = \phi(x)\) であって \(x\) が \(A\) から \(B\) に増加するとき \(a\) から \(b\) へ単調に増加するものが存在する。
この結果は §108 の定理を使わずとも直接得られる。\(A \lt \xi \lt B\) に対して \(a \lt y \lt b\) かつ \(F(y) \leq \xi\) が成り立つ \(y\) の集合を考える。この集合には上限 \(\eta\) が存在し、この \(\eta\) に対して \(F(\eta) \leq \xi\) が成り立つ。\(F(\eta)\) が \(\xi\) より小さいとすると、\(y \gt \eta\) かつ \(F(y) \lt \xi\) となるような \(y\) が存在することになるが、このとき \(\eta\) は考えている集合の上限となれない。よって \(F(\eta) = \xi\) であり、方程式 \(F(y) = \xi\) は唯一の解 \(y = \eta = \phi(\xi)\) を持つ。\(\eta\) が \(\xi\) と共に連続かつ単調に増加することも示せるので、定理が証明される。
第五章に関するその他の例
-
\(a\) と \(b\) が \(0\) でないなら \[ ax^{n} + bx^{n-1} + \cdots + k = ax^{n} (1 + \varepsilon_{x}) \] が成り立つ。ここで \(\varepsilon_{x}\) は \(x\) が大きいときに一次の小ささを持つ式を表す。
-
\(P(x) = ax^{n} + bx^{n-1} + \cdots + k\) で \(a\) が \(0\) でないとする。\(x\) を大きくしていくと、いずれ \(P(x)\) は \(a\) と同じ符号を持つようになる。また任意の正の定数 \(\lambda\) に対する \(P(x + \lambda) - P(x)\) も同様の振る舞いをする。
-
一般に \[ \dfrac{ax^{n} + bx^{n-1} + \cdots + k}{Ax^{n} + Bx^{n-1} + \cdots + K} = \alpha + \frac{\beta}{x}(1 + \varepsilon_{x}) \] だと示せ。ここで \(\alpha = a/A,\ \beta = (bA - aB)/A^{2}\) で、\(\varepsilon_{x}\) は \(x\) が大きいときに一次の小ささを持つ式とする。例外的な場合を全て示せ。
-
式 \[ \frac{ax^{2} + bx + c}{Ax^{2} + Bx + C} \] を次の形で表せ: \[ \alpha + \frac{\beta}{x} + (1 + \varepsilon_{x})\frac{\gamma}{x^{2}} \] ここで \(\varepsilon_{x}\) は \(x\) が大きいときに一次の小ささを持つ式とする。
-
次を示せ: \[ \lim_{x\to\infty}\sqrt{x}\{\sqrt{x + a} - \sqrt{x}\} = \dfrac{1}{2} a \]
[等式 \(\sqrt{x + a} - \sqrt{x} = \dfrac{a}{\sqrt{x + a} + \sqrt{x}}\) を使う]
-
\(\sqrt{x + a} = \sqrt{x} + \dfrac{a}{2\sqrt{x}} (1 + \varepsilon_{x})\) を示せ。\(\varepsilon_{x}\) は \(x\) が大きいときに一次の大きさを持つ式とする。
-
\(x \to \infty\) で \(\sqrt{a x^{2} + 2bx + c} - \alpha x - \beta\) が \(0\) に向かうような \(\alpha\) と \(\beta\) を求めよ。そのとき \(\displaystyle \lim_{x \to \infty} x\{\sqrt{ax^{2} + 2bx + c} - \alpha x - \beta\} = (ac - b^{2})/2a\) だと示せ。
-
次の値を求めよ: \[ \lim_{x \to\infty} x\left\{\sqrt{x^{2} + \sqrt{x^{4} + 1}} - x\sqrt{2}\right\} \]
-
\(x \to \dfrac{1}{2}\pi\) のとき \((\sec x - \tan x) \to 0\) だと示せ。
-
\(x\) が小さいとき \(\phi(x) = 1 - \cos(1 - \cos x)\) は四次の小ささを持つと示し、\(x \to 0\) における \(\phi(x)/x^{4}\) の極限を求めよ。
-
\(x\) が小さいとき \(\phi(x) = x\sin(\sin x) - \sin^{2}x\) は六次の小ささを持つと示し、\(x \to 0\) における \(\phi(x)/x^{6}\) の極限を求めよ。
-
円の半径 \(OA\) を外側に伸ばし、その上に点 \(P\) を取る。\(P\) から円に引いた接線の接点を \(T\) として、\(T\) から \(OA\) に向かって伸ばした垂線の足を \(N\) とする。\(P\) が \(A\) に近づくとき \(NA/AP \to 1\) だと示せ。
-
円弧の端点および中点で接線を引く。円弧の端点を通る接線と円弧の弦からなる三角形の面積を \(\Delta\) とし、三本の接線で囲まれた領域の面積を \(\Delta'\) とする。弧の長さが \(0\) に向かうとき \(\Delta/\Delta' \to 4\) だと示せ。
-
\(x \to 0\) で \(\{a + \sin(1/x)\}/x\) が \(\infty\) および \(-\infty\) に向かうための条件はそれぞれ何か? [\(a \gt 1\) なら \(\infty\) に向かい、\(a \lt -1\) なら \(-\infty\) に向かう。\(-1 \leq a \leq 1\) なら振動する]
-
\(x\) が有理数 \(p/q\) のとき \(\phi(x) = 1/q\) で、\(x\) が無理数のとき \(\phi(x) = 0\) とする。この \(\phi(x)\) は全ての無理数 \(x\) で連続で、全ての有理数 \(x\) で不連続となる。
-
次の二つの関数のグラフが、どちらも 図 32 となること示せ; \[ 1 - x + [x] - [1 - x],\quad 1 - x - \lim_{n\to\infty} (\cos^{2n+1}\pi x) \]
-
\(x = 0\) で \(0\) となり、\(0 \lt x \lt \frac{1}{2}\) で \(\frac{1}{2} - x\) となり、\(x = \frac{1}{2}\) で \(\frac{1}{2}\) となり、\(\frac{1}{2} \lt x \lt 1\) で \(\frac{3}{2} - x\) となり、\(x = 1\) で \(1\) となる関数 \(\phi(x)\) を考える。\(x\) が \(0\) から \(1\) まで増加するとき \(\phi(x)\) は \(0\) から \(1\) の値をちょうど一度ずつ取るものの、\(\phi(x)\) は \(x = 0,\ x = \frac{1}{2},\ x = 1\) で不連続だと示せ。また \(\phi(x)\) が \[ \dfrac{1}{2} - x - \dfrac{1}{2}[2x] - \dfrac{1}{2}[1 - 2x] \] と表せることを示せ。
-
\(x\) が有理数のとき \(\phi(x) = x\) で、\(x\) が無理数のとき \(\phi(x) = 1 - x\) と定める。\(x\) が \(0\) から \(1\) まで増加するとき \(\phi(x)\) は \(0\) から \(1\) までの全ての値を取るものの、\(\phi(x)\) は \(x = \frac{1}{2}\) を除いた全ての値で不連続だと示せ。
-
\(x\) が \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) まで増加するとき \(y = \sin x\) は連続で、\(-1\) から \(1\) まで狭義単調増加する。\(y = -1\) から \(y = 1\) まで連続かつ単調増加な関数 \(x = \arcsin y\) の存在を導け。
-
最も原点に近い \(\arctan y\) の値は全ての \(y\) に対して連続であり、\(y\) が全ての実数を動くとき \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) まで単調に増加することを示せ。
-
§108–§109 と同じ方法で、\(x = 0,\ y = 0\) の近傍における方程式 \[ \begin{gathered} y^{2} - y - x = 0,\quad y^{4} - y^{2} - x^{2} = 0,\quad y^{4} - y^{2} + x^{2} = 0 \end{gathered} \] の解について議論せよ。
-
\(ax^{2} + 2bxy + cy^{2} + 2dx + 2ey = 0\) および \(\Delta = 2bde - ae^{2} - cd^{2}\) とする。このとき \(y\) が \(y = \alpha x + \beta x^{2} + (\gamma + \varepsilon_{x}) x^{3}\) で与えられると示せ。ここで \[ \begin{aligned} \alpha & = -\frac{d}{e},\quad \beta & = \frac{\Delta}{2e^{3}},\quad \gamma & = \frac{(cd - be) \Delta}{2e^{5}} \end{aligned} \] であり、\(\varepsilon_{x}\) は \(x\) が小さいときに一次の小ささを持つ式を表す。
[\(y - \alpha x = \eta\) とすれば \[ \begin{aligned} -2e\eta & = ax^{2} + 2bx(\eta + \alpha x) + c(\eta + \alpha x)^{2} \\ & = Ax^{2} + 2Bx \eta + C\eta^{2} \end{aligned} \] なので、\(\eta\) は二次の小ささ、\(x\eta\) は三次の小ささ、\(\eta^{2}\) は四次の小ささを持つ。よって \(-2e\eta = Ax^{2} - (AB/e) x^{3}\) とすれば誤差は四次となる]
-
\(x = ay + by^{2} + cy^{3}\) なら、\(y\) の一つは \[ y = \alpha x + \beta x^{2} + (\gamma + \varepsilon_{x}) x^{3} \] と表せる。ここで \(\alpha = 1/a,\ \beta = -b/a^{3},\ \gamma = (2b^{2} - ac)/a^{5}\) であり、\(\varepsilon\) は \(x\) が小さいときに一次の大きさを持つ式を表す。
-
\(n\) が \(2\) 以上の整数で、\(x = ay + by^{n}\) が成り立つとする。このとき \(y\) の一つは \(y = \alpha x + \beta x^{n} + (\gamma + \varepsilon_{x}) x^{2n-1}\) と表せる。ここで \(\alpha = 1/a,\ \beta = -b/a^{n+1}\) および \(\gamma = nb^{2}/a^{2n+1}\) で、\(\varepsilon_{x}\) は \(x\) が小さいときに \(n - 1\) 次の小ささを持つ式を表す。
-
\(xy = \sin x\) の最も小さい正の解が \([0, 1]\) で連続な \(y\) の関数であり、\(y\) が \(0\) から \(1\) まで増加するとき \(\pi\) から \(0\) まで単調に減少することを示せ。 [この関数は \(\sin x/x\) の逆関数であり、§109 の結果を適用できる]
-
\(xy = \tan x\) の最も小さい正の解が \([1, \infty]\) で連続な \(y\) の関数であり、\(y\) が \(1\) から \(\infty\) まで増加するとき \(0\) から \(\frac{1}{2}\pi\) まで単調に増加すると示せ。
-
つまりこの章で \(\sqrt{x}\) は一価関数 \(+\sqrt{x}\) だけを表し、§26 のような \( +\sqrt{x}\) と \(-\sqrt{x}\) の二つの値を取る二価関数は表さないとする。[return]
-
\(\infty\) を使って \(x \to \infty,\ \phi(x) \to \infty\) と書く代わりに、\(+\infty\) を使って \(x \to +\infty,\ \phi(x) \to +\infty\) と書いた方が分かりやすい場合もある。[return]
-
§62 では \(|\phi(n)| \lt K\) が全ての \(n\) で成り立つとき有限に振動すると定義し、\(n \geq n_{0}\) という条件は定義に使わなかった。しかし \(\phi(n)\) を考えるなら二つの定義は同値である: もし \(n \geq n_{0}\) で \(|\phi(n) \lt K|\) なら、\(|\phi(1)|,\ |\phi(2)|,\ \ldots,\ |\phi(n_{0} - 1)|\) と \(K\) の最大値を \(K'\) とすれば全ての \(n\) に対して \(|\phi(n)| \lt K'\) が成り立つ。しかし連続変数では \(x_{0}\) より小さい \(x\) が無限に存在するので、\(x \geq x_{0}\) を考えると話が難しくなる。[return]
-
例えば §93 の定義では \(0 \lt y \leq y_{0}\) を満たす \(y\) を考えている。この不等式の最初の不等号が \(y = 0\) の場合を除いている。[return]
-
ここからの問題は \(x \to 0\) の極限を求める問題とする。[return]
-
この不等式の証明には「扇形に内接する三角形の面積は扇形の面積よりも小さい」といった扇形の面積の性質が使われる。こういった性質は幾何学的に自明とされることが多い。この仮定の正当化は第七章で行う。[return]
-
\(\beta = b\) なら、以降の議論で \([\beta - \eta, \beta + \eta]\) を \([\beta - \eta, \beta]\) に、\(\beta + \eta\) を \(\beta\) に置き換える。[return]
-
この重なる (overlap) という言葉は通常の意味で使われている: つまり「端点でない共通の点が存在する」を意味する。例えば \([0, \frac{2}{3}]\) と \([\frac{1}{3}, 1]\) は重なる。\([0, \frac{1}{2}]\) と \([\frac{1}{2}, 1]\) のような区間の組は接する (abut) と言う。[return]
-
「内部にある」は「含まれてかつ端点でない」を意味する。[return]
-
この定義を図示してみるとよい。[return]