§152 多変数関数の微分 (その 1)
ここまでは \(x\) という一つの変数の関数だけを考えてきた。しかし微分の考え方を \(x,\ y,\ \ldots\) という複数の変数の関数に拡張するのを妨げるものは何もない。
\(f(x, y)\) を二つの1実変数 \(x\) と \(y\) の関数として、極限 \[ \lim_{h\to 0}\frac{f(x + h, y) - f(x, y)}{h},\quad \lim_{k\to 0}\frac{f(x, y + k) - f(x, y)}{k} \] が考えている全ての \(x\) と \(y\) に対して存在すると仮定する。つまり \(f(x, y)\) が \(x\) に関する導関数 \(df/dx = D_{x}f(x, y)\) を持ち、さらに \(y\) に関する導関数 \(df/dy = D_{y}f(x, y)\) も持つとする。こういった導関数は \(f\) の偏微分係数 (partial differential coefficients) と呼ばれ、 \[ \frac{\partial f}{\partial x},\quad \frac{\partial f}{\partial y} \] あるいは \[ f_{x}'(x, y),\quad f_{y}'(x, y) \] と表記される。\(f_{x}',\ f_{y}'\) や \(f_{x},\ f_{y}\) と書かれることもある。ただしここで、こういった記法が本質的に新しい概念を定義していると考えてはいけない。\(x\) に関する "偏微分" は、手続きとして通常の微分と全く同一である。\(f\) が \(x\) とは独立な二つ目の引数 \(y\) を取る点にだけ気を付ければよい。
ここまでの議論は \(x\) と \(y\) が互いに独立だとして進めてきた。\(x\) と \(y\) が何らかの関係で結ばれているなら、話は大きく変わってくる。この場合 \(y\) を変えずに \(x\) を \(x + h\) に変えることができないので、上述の \(f_{x}'\) の定義が全く意味をなさなくなる。ただしこのとき \(f(x, y)\) は本当の意味で二変数関数ではない。第二章で定義した通り、二変数関数とは二つの独立変数を持つ関数である。\(y\) が \(x\) に依存しているなら、\(y\) は \(x\) の関数となる。この関数を \(y = \phi(x)\) と書けば \[ f(x, y) = f\{x, \phi(x)\} \] が単一の変数 \(x\) の関数に過ぎないことがはっきりする。もちろん \(f\) は単一の変数 \(y\) の関数としても表せる。あるいは \(x\) と \(y\) を第三の変数 \(t\) の関数とみなしたほうが分かりやすい場合も往々にしてある。このとき \(f(x, y)\) は \(f\{\phi(t), \psi(t)\}\) という形で表すことができ、単一の変数 \(t\) の関数となる。
-
\(x = r\cos\theta\) かつ \(y = r\sin\theta\) なら \(r = \sqrt{x^{2} + y^{2}}\) と \(\theta = \arctan(y/x)\) が成り立つ。このとき \[ \begin{aligned} \frac{\partial r}{\partial x} & = \frac{x}{\sqrt{x^{2} + y^{2}}}, & \frac{\partial r}{\partial y} & = \frac{y}{\sqrt{x^{2} + y^{2}}}, & \frac{\partial \theta}{\partial x} & = -\frac{y}{x^{2} + y^{2}}, & \frac{\partial \theta}{\partial y} & = \frac{x}{x^{2} + y^{2}},\\ \frac{\partial x}{\partial r} & = \cos\theta, & \frac{\partial y}{\partial r} & = \sin\theta, & \frac{\partial x}{\partial \theta} & = -r\sin\theta, & \frac{\partial y}{\partial \theta} & = r\cos\theta \end{aligned} \] を示せ。
-
\(\dfrac{\partial r}{\partial x}\neq 1\bigg/\biggl(\dfrac{\partial x}{\partial r}\biggr)\) と \(\dfrac{\partial \theta}{\partial x}\neq 1\bigg/\biggl(\dfrac{\partial x}{\partial \theta}\biggr)\) を説明せよ。
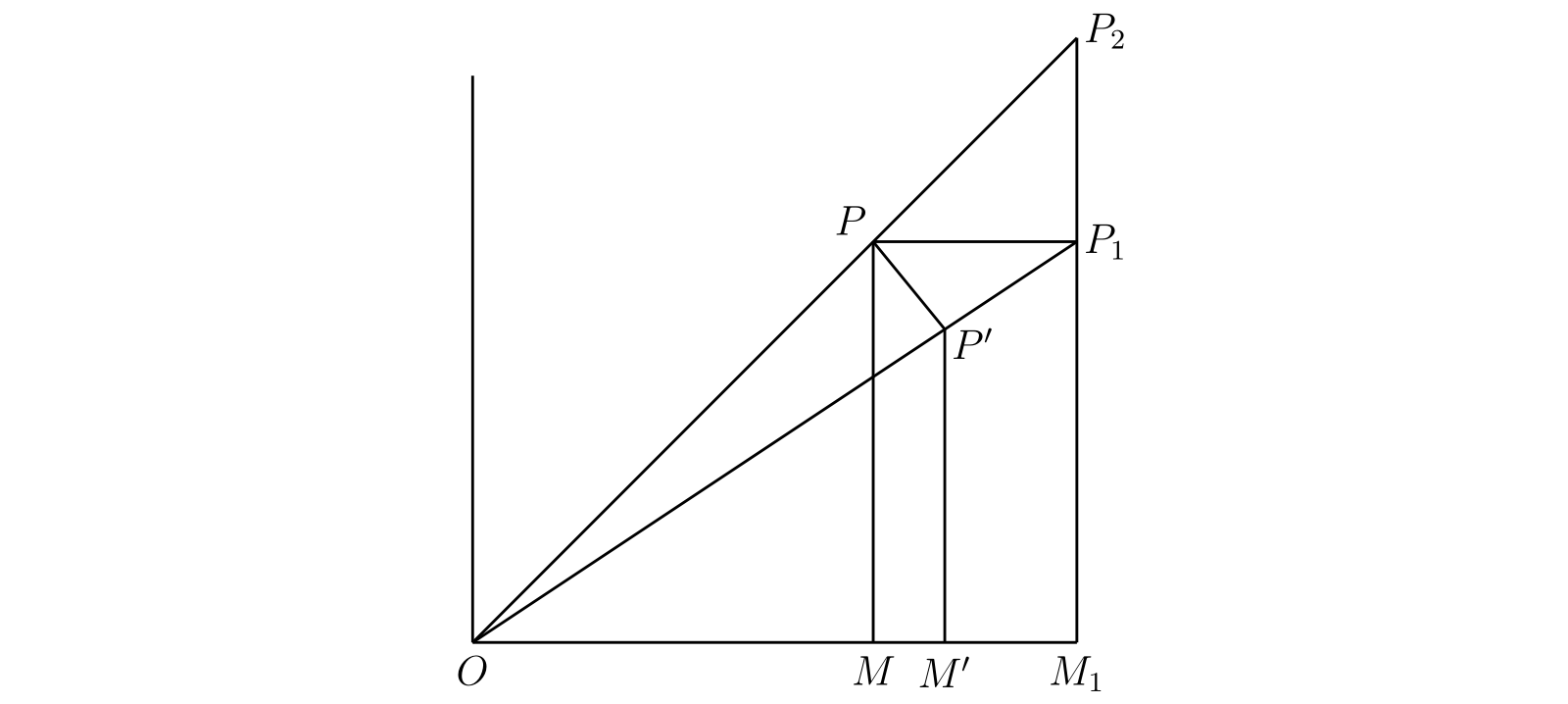 図 46
図 46[考えているのが単一の変数 \(x\) の関数 \(y\) のときは \(dy/dx\) と \(dx/dy\) の定義が互いの逆数であり、等号が成り立つ。しかし二変数関数ではこれは成り立たない。図 46 で \(P\) を点 \((x, y)\) あるいは \((r, \theta)\) とする。\(\partial r/\partial x\) を求めるには、\(y\) を定数に保ったまま \(x\) を増加させる必要がある。\(x\) の増分を \(MM_{1} = \delta x\) として、\(P\) の移動先を \(P_{1}\) とする。\(OP_{1}\) 上に \(OP' = OP\) となる \(P'\) を取ると、\(r\) の増分を \(P'P_{1} = \delta r\) と表せる。そして \(\partial r/\partial x = \lim(\delta r/\delta x)\) が成り立つ。一方で \(\partial x/\partial r\) を計算するには、\(x\) と \(y\) を \(r\) と \(\theta\) の関数とみなした上で \(\theta\) を一定に保ったまま \(r\) を \(\Delta r\) だけ増加させる必要がある。これによって \(P\) は \(P_{2}\) まで移動し、\(PP_{2} = \Delta r\) が成り立つ。対応する \(x\) の増分を \(MM_{1} = \Delta x\) とすれば \[ \frac{\partial x}{\partial r} = \lim \frac{\Delta x}{\Delta r} \] が成り立つ。すると \(\Delta x = \delta x\)2 かつ \(\Delta r \neq \delta r\) となる。実際 \[ \lim \frac{\delta r}{\delta x} = \lim \frac{P'P_{1}}{PP_{1}} = \cos\theta \] だが \[ \lim \frac{\Delta r}{\Delta x} = \lim \frac{PP_{2}}{PP_{1}} = \sec\theta \] であり、ここから \[ \lim \frac{\delta r}{\Delta r} = \cos^{2}\theta \] が分かる。
この関係の背後にあるのはもちろん\(\bm{\partial x/\partial r}\) と \(\bm{\partial r/\partial x}\) では \(\bm{P}\) の変動についての仮定が異なるという事実である]
-
\(z = f(ax + by)\) なら \(b\dfrac{\partial z}{\partial x} = a\dfrac{\partial z}{\partial y}\) だと示せ。
-
\(X + Y = x,\ Y = xy\) として \(\dfrac{\partial X}{\partial x},\ \dfrac{\partial X}{\partial y}\,\ \ldots\) を求めよ。\(x\) と \(y\) を \(X,\ Y\) の関数として表し、\(\dfrac{\partial x}{\partial X},\ \dfrac{\partial x}{\partial Y},\ \ldots\) を求めよ。
-
\(X + Y + Z = x,\ Y + Z = xy,\ Z = xyz\) として \(\dfrac{\partial X}{\partial x},\ \ldots\) を求めよ。\(X,\ Y,\ Z\) を使って \(x,\ y,\ z\) を表し、\(\dfrac{\partial x}{\partial X},\ \ldots\) を求めよ。
[この節の議論は任意の数の関数へと容易に拡張できる。ただし、複数の変数を持つ関数の偏微分は全ての独立変数が指定されてはじめて定義される点に注意が必要となる。例えば \(u = x + y + z\) で \(x,\ y,\ z\) が独立変数なら \(\partial u/\partial x = 1\) だが、\(u\) が \(x,\ x + y = \eta,\ x + y + z = \zeta\) という変数の関数だとすれば \(u = \zeta\) および \(\partial u/\partial x = 0\) となる]